金属管浮子流量计检测方法及其实验装置不确定度评定

牛立娜 赵 宁 陈世砚 田鹏飞 李国栋

(1.河北省计量监督检测院，石家庄 050051；2.河北大学，保定 071000)



金属管浮子流量计检测方法及其实验装置不确定度评定

牛立娜1赵 宁2陈世砚1田鹏飞1李国栋1

(1.河北省计量监督检测院，石家庄 050051；2.河北大学，保定 071000)

针对常压气体检测设备无法模拟金属管浮子流量计高压工况状态，更无从得知其计量准确性这一现状进行研究，提出了一种具体可行的检测方法：即采用空气压缩机和高压储气罐模拟金属管浮子流量计标称压力状态，经过两次逐级减压系统后流入金属管浮子流量计，最终通过缓冲罐进入钟罩式气体流量标准装置内进行检测，并对其实验装置进行不确定度评定，结果表明该装置可以满足金属管浮子流量计日常检定、校准工作。

金属管浮子流量计；检测方法；实验装置；不确定度分量；评定

0 引言

浮子流量计又名转子流量计或面积流量计[1]，随着医药化工行业的发展，产品质量控制日益精进，金属管浮子流量计作为工艺控制设备广泛应用于产品的生产环节，测量介质多为氮气、氢气、氧气、空气等。本文主要研究以气体为介质、工作压力在0.05～1.5MPa，测量上限在100m3/h以内的金属管浮子流量计的检测校准方法。

1 检测方法

根据国际建议，气体浮子流量计的检测方法主要有容积法、标准表法两种[2]。针对金属管浮子流量计特殊的高压检测需求，我们设计了一种基于容积法的检测方法，即将高压空气经过两次逐级减压后通过金属管浮子流量计，最终通过缓冲罐进入钟罩式气体流量标准装置内。通过钟罩标准器修正示值与金属管浮子示值比对达到检测目的。

2 实验装置构成

实验装置主要由六部分组成，即空气压缩机、高压储气罐、减压系统、缓冲罐、钟罩及温压监控仪表，示意图详见图1。

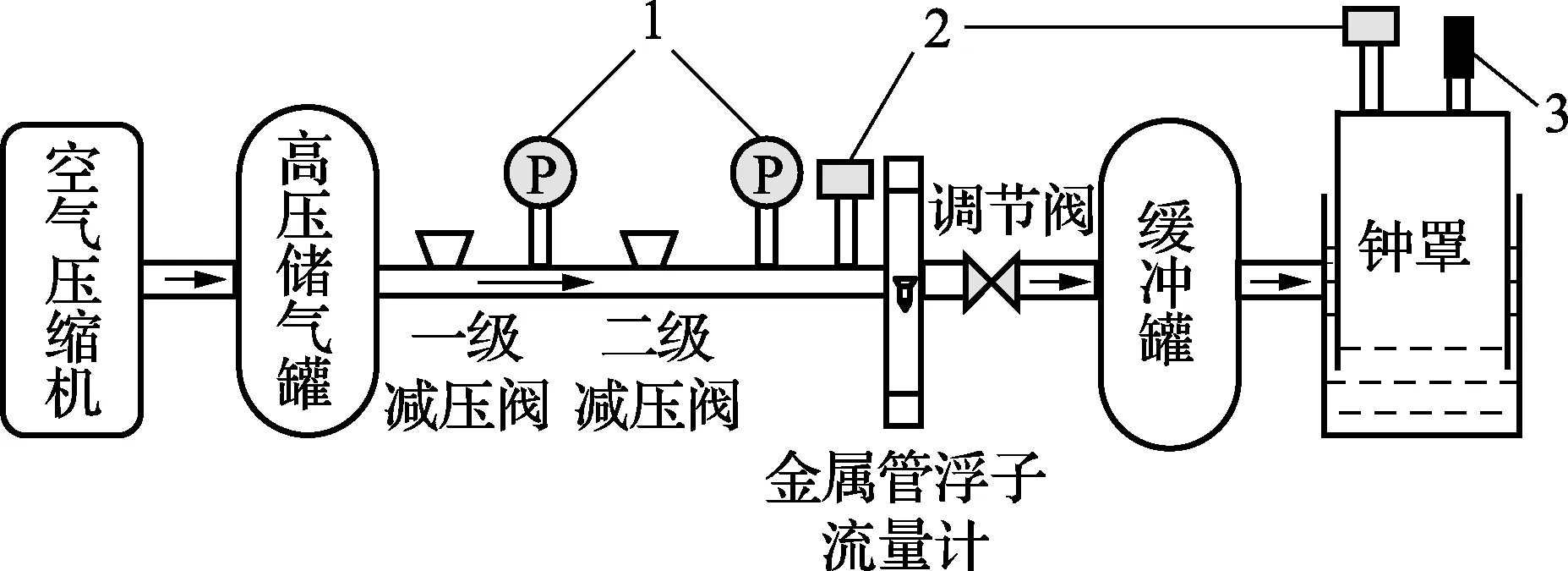
1. 0.25级精密压力表；2.A级工业铂电阻；3.0.1级压力传感器图1 实验装置示意图

3 数学模型[3]

根据上述检测方法，按下式计算流量计在标准(刻度)状态下的实际流量qN：

(1)

式中：V为流入钟罩内的气体体积，m3；t为流入的时间，h；pN，pS，pm分别为刻度状态、气体装置内、流量计入口处的气体绝对压力，MPa；TN，TS，Tm分别为刻度状态、气体装置内、流量计入口处的气体热力学温度，K；ρSM，ρSN分别为检定用介质和刻度用介质在标准(刻度)状态下的密度。

4 不确定度分量

金属浮子流量计生产投入市场，刻度介质、刻度状态已经确定，即ρSM，ρSN，TN，pN为已知常数，对式(1)两边取ln，求偏导数，易知ur(ρSM)=ur(ρSN)=ur(TN)=ur(pN)≈0，则式(1)简化为：

(2)

1)标准容器钟罩累积体积V引入的相对标准不确定度分量ur(V)

钟罩标准装置容积由0.025级二等标准金属量器进行量值传递，标准容积的相对不确定度：

urA(V)=0.11%；urB(V)=0.12%

由标准容器V引入的相对标准不确定分量为：

2)测量时间t引入的相对标准不确定度分量ur(t)

同步测量时间使用自动计控系统内石英晶体振荡器，铷原子频率标准装置对其进行校准结果为：

Ur(t)=3.6×10-7，k=2，则其相对标准不确定度分量为：

3)钟罩装置内压力测量pS引入的相对标准不确定度分量ur(pS)

钟罩内压力采集选用0.2级压力传感器，服从正态分布，包含因子k=2，则由压力传感器引入的相对标准不确定度分量为：

4)钟罩装置内温度测量TS引入的相对标准不确定度分量ur(TS)

钟罩内温度采集选用A级工业铂电阻，其最大允许误差为±0.2K，服从均匀分布，包含因子k=2，假设测量温度为293.15K，则其相对标准不确定度分量为：

5)流量计入口处压力测量pm引入的相对标准不确定度分量ur(pm)

流量计入口处压力测量选用0.25级精密压力表，服从正态分布，包含因子k=2，则其相对标准不确定度分量为：

6)流量计入口处温度测量Tm引入的相对标准不确定度分量ur(Tm)

流量计入口处温度测量受两方面因素的影响，一方面来自于温度采集设备，一方面来自压力变化导致温度变化。

流量计入口处温度测量同样选用A级工业铂电阻，其最大允许误差为±0.2K，服从均匀分布，包含因子k=2，假设测量温度为293.15K，则其相对标准不确定度分量为：

压力变化导致温度变化，通过表1分析：温度测量时间选定在5min内和10min以后进行测量均值相差0.172℃，则A级工业铂电阻测量反应迟滞引入的不确定度分量为：

表1 实验数据

5 合成标准不确定度

将上述不确定度分量按照式(2)合成相对标准不确定度，具体参数详见表2。

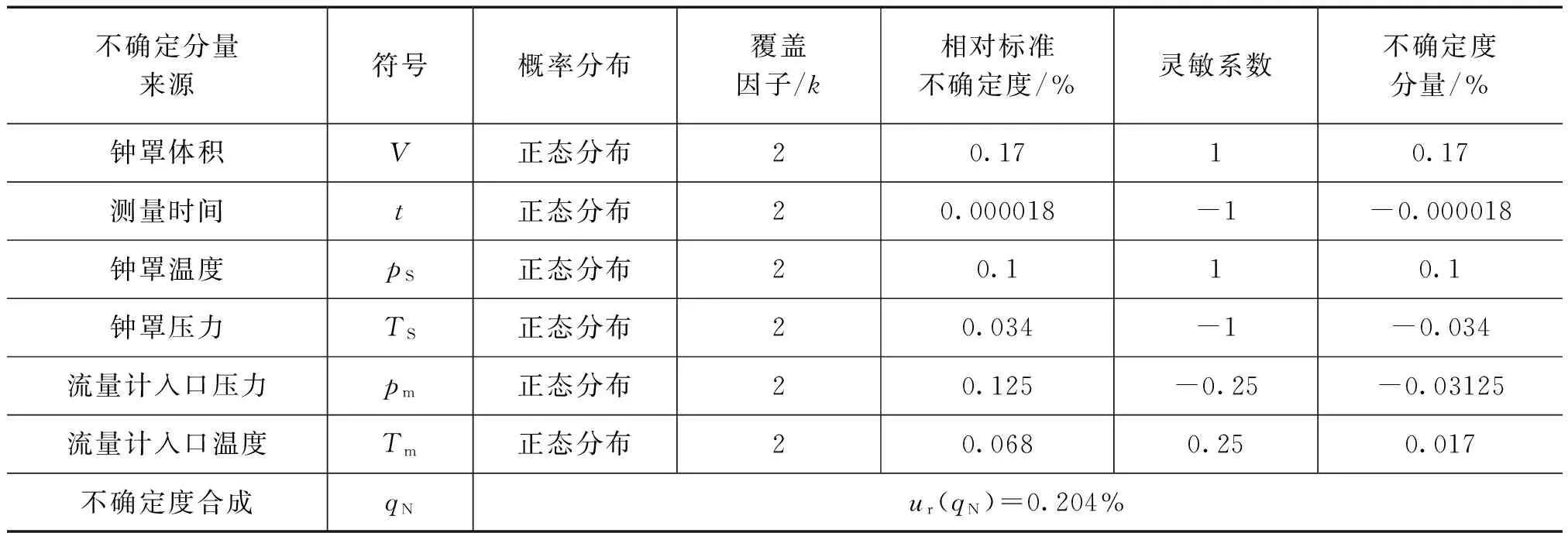
表2 合成相对标准不确定度

6 扩展不确定度

日常的检定要求置信概率为95%，包含因子k=2，所以整套检定装置的扩展不确定度为：

Ur=kur(qN)=2×0.204%=0.41%

7 结束语

本文对金属管浮子流量计提出的可行性检测方法所用实验装置进行了全面的不确定度分析，评定结果满足检定规程JJG 257—2007的要求。因此利用该检定装置可以开展金属管浮子流量计量检测工作。

[1] 苏彦勋，梁国伟，盛健.流量计量与测试[M].北京：中国计量出版社，2007：179-195

[2] JJG 257—2007浮子流量计[S]

[3] 李金海.误差理论与测量不确定度评定[M].北京：中国计量出版社，2003：108-157

[4] 吴诚玲，王钰.浮子流量计不确定度评定[J].计量与测试技术，2013(4)：72-73

[5] 孙仁伟.浮子流量计的发展介绍[J].自动化与仪表，2005(5)：33-35

10.3969/j.issn.1000-0771.2015.3.16