超高排土场的本体稳定性敏感分析
王 涛 贾洪彪* 李 超
(中国地质大学(武汉)工程学院,湖北 武汉 430074)
超高排土场的本体稳定性敏感分析
王 涛 贾洪彪* 李 超
(中国地质大学(武汉)工程学院,湖北 武汉 430074)
结合跑马岭排土场的工程地质条件,建立了该排土场的三维整体模型,采用正交设计和方差分析研究了影响超高排土场本体失稳的各因素敏感性,得出的结论对排土场的建设具有很强的实践意义。
超高排土场,稳定性,本体滑坡,影响因素
目前,我国现有各类大型排土场几万座,露天矿排土场用地约占矿山总用地的30%~50%[1],其常见的地质灾害问题是滑坡和泥石流。由于露天排土场堆积量是矿山追求的经济目标之一,同时随着排土场堆积量的增加,滑坡和泥石流的威胁随之增大,因此排土场安全与经济之间存在矛盾。
许多学者参照土质边坡或者土石坝,利用不同研究方法,对地域性排土场的边坡稳定性进行了分析研究[2-7]。目前,关于排土场边坡的敏感性分析较少,尤其是对于超高排土场的边坡研究较少。
1 跑马岭排土场整体分析
1.1 工程地质条件及现状
跑马岭排土场是某铁矿一大型排土场,从地形条件上分析比较适宜做排土场。从环境影响而言,下游有村庄和工厂,并有公路通过。该排土场典型剖面如图1所示。该排土场的安全使用对整个矿区至为关键。

在对排土场进行实地勘察时发现,在坡顶位置已经出现了数条大小、长短不一的裂缝,坡面也有明显的鼓出。初步分析这些裂缝的产生是由于废渣堆排后,固结过程中不均匀沉降产生的,虽然裂缝发育相对较新,但是受到暴雨或者其他外力作用时,极有可能出现本体失稳。
通过现场试验及室内试验分析得排土场各地层的强度参数,见表1。

表1 排土场各层物理力学参数
1.2 模拟分析
首先建立跑马岭排土场的地质模拟模型,进行网格划分,根据工程地质条件,输入地质参数及边界条件等。模拟天然工况下其状态,并采用强度折减法,得到其整体稳定系数为1.54。从模拟结果可以看出,排土场的自堆排至稳定阶段,其最大位移出现在排土场坡顶处,下沉量自坡顶至坡脚逐渐减小;排土场散体内三轴方向的应力值都随深度增大,破坏区范围很小,说明排土场在天然状态下整体是稳定的。
排土场边坡的浅层稳定性相对较差,易于出现开裂破坏以及剪切破坏,甚至于滑坡。而沿排土场与基底接触面以及基底内部位移较小,多以蠕变变形为主,也就是说排土场整体是相对稳定的。
2 影响排土场本体稳定性因素分析
通过前期对该排土场整体稳定性的分析以及评价得出:该排土场出现沿面滑坡或基础滑坡的可能性较小;有可能出现本体滑坡。因此,分析影响排土场本体滑坡因素的敏感性。
2.1 影响因素敏感性试验设计及模拟
在不影响计算结果的基础上,为了计算上的简便将排土场的边坡进行简化,选取排土场前缘范围区域,建立简化三维模型,见图2。

其次,根据前期的研究以及跑马岭排土场的工程地质条件,在综合分析后得出影响其本体滑坡的因素:散体的力学性质、边坡角、颗粒分级程度以及边坡高度。依据该排土场试验和研究的成果,同时结合工程地质经验类比综合以及参照文献,对该排土场进行分层设置物理力学参数,使其符合实际情况,进而体现排土场的颗粒分级情况,参数详细设置见表2。

表2 排土场组合土体力学参数
根据影响该排土场本体滑坡的主要因素,本文选取散体的力学性质、土层水平划分(代表颗粒分级程度)、坡角和坡高四种因素进行敏感性分析,试验指标为稳定性系数Fos。各因素取值范围按一般工程经验和前期试验分析结果确定,并将其量化为4个水平,见表3。

表3 因素水平表
选取正交表时,不考虑这4种因素间的交互作用,且预留空列作为误差列,即设计5因素4水平试验,选取L16(45)正交表。根据正交表设计方案以及前期对排土场本体滑坡研究,利用有限元强度折减法求得最危险滑面及相应的安全系数Fos,设计方案及计算结果见表4。

表4 正交试验设计方案及计算结果
2.2 试验结果分析
首先从计算过程及结果来看,排土场边坡发生破坏的地方主要是排土场本体,这与本试验初始设定的条件一致,说明本试验设计符合实际。
如表4所示,对正交试验试验结果进行分析。设定不考虑各因素间的相互影响作用,则正交表L16(45)各列的自由度均为3,空列为误差列,自由度亦为3。根据相关公式计算出各列偏差平方和、自由度、方差及F值。在正交试验中进行显著性检验之前,先把各因素及交互作用的方差(MS因)与误差项方差(MSe)进行比较,当MS因≤2MSe时,将此因素的平方和归入误差平方和,其自由度归入误差项自由度,使误差项自由度增大,提高了F检验灵敏度。根据此原则,判断因素B的偏差平方和较小,并入误差的偏差平方和及自由度,并认为土层分层因素对排土场边坡稳定性无显著影响。
查F分布表可得知:F1-0.1(3,6)=3.29;F1-0.05(3,6)=4.76;
F1-0.01(3,6)=9.78。根据已经给出的显著性水平分级方法,将4种因素对本体滑坡影响的显著性水平进行分级,方差分析结果详见表5。
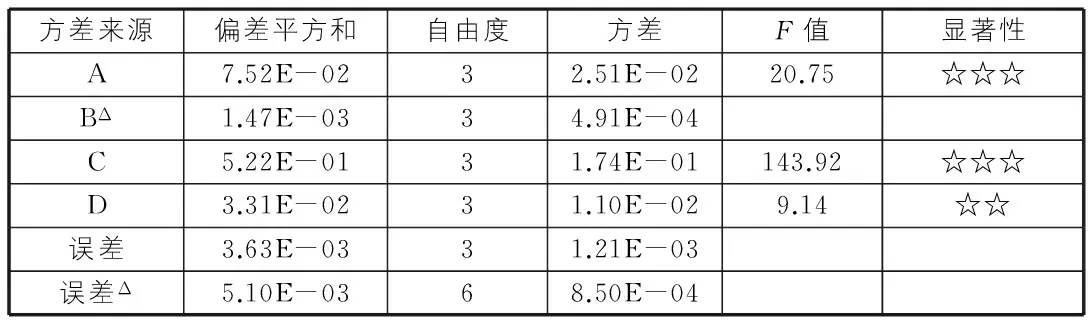
表5 方差分析结果
由方差分析结果可以得出结论:
通过方差分析结果表5中各因素平均偏差平方和的大小顺序,可以看出4种因素的敏感性由大到小依次为坡角、散体的力学性质、坡高、土层分布的划分。我们可以看出,排土场散体的力学性质、坡角及坡高在排土场本体稳定性中的重要位置,尤其是坡角对边坡自身稳定性起着决定性的作用。
3 结语
本文建立跑马岭排土场整体的三维模型,分析了排土场边坡的稳定性,并分析了影响超高排土场本体滑坡的各因素敏感性。通过分析结果得出:1)该排土场在自然工况下整体稳定性良好,局部可能会出现小滑坡。即该排土场出现沿面滑坡或基础滑坡的可能性较小,可能会存在本体滑坡。2)散体的力学性质、坡角对排土场边坡稳定性影响特别显著,坡高对排土场边坡稳定性影响显著,而散体土层分布的划分范围对排土场边坡稳定性基本无影响。对于复杂超高排土场,细致分析排土场内部应力分布、变形破坏的特征,更好评价排土场稳定性,找到影响山区排土场稳定性的关键因素及其次要因素,并对指导排土场的建设具有很强的实践意义。
[1] 孙世国,杨 宏,冉启发,等.典型排土场边坡稳定性控制技术[M].北京:冶金工业出版社,2011.
[2] 许旭堂,简文彬.兰桥排土场边坡失稳模式及其稳定性数值分析[J].防灾减灾工程学报,2013,33(6):686-690.
[3] 汪海滨,李小春.排土场空间效应及其稳定性评价方法研究[J].岩石力学与工程学报,2011,30(10):125-129.
[4] 王光进,杨春和,张 超,等.超高排土场的粒径分级及其边坡稳定性分析研究[J].岩土力学,2011,32(3):905-910.
[5] 任 伟,李小春,汪海滨,等.排土场级配规律及其对稳定性影响的模型试验研究[J].长江科学院院报,2012,29(8):100-105.
[6] 张 超,杨春和.粗粒料强度准则与排土场稳定性研究[J].岩土力学,2014,35(3):641-646.
[7] 倪 恒,刘佑荣,龙治国.正交设计在滑坡敏感性分析中的应用[J].岩石力学与工程学报,2002,21(7):989-992.
[8] 李志西,杜双奎.试验优化设计与统计分析[M].北京:科学出版社,2010.
Sensitive analysis of factors affecting super-high waste dump stability of itself
Wang Tao Jia Hongbiao* Li Chao
(FacultyofEngineering,ChinaUniversityofGeosciences,Wuhan430074,China)
Combining the engineering geological condition of Paomaling waste dump, established the 3D mode of the whole dump, the effects on the sensitivity of the unstable super-high waste dump itself is studied by using the orthogonal design and variance analysis, the conclusion had strong practical significance for the construction of dump.
super-high waste dump, stability, body landslide, influencing factors
2015-01-08
王 涛(1989- ),男,在读硕士; 李 超(1990- ),男,在读硕士
贾洪彪(1969- ),男,教授
1009-6825(2015)08-0075-02
P642.2
A

