基于浮动车数据的路口探测方法

谭 祥 爽，王 静 ，宋 现 锋,*，许 长 辉，汪 超 亮

(1.中国科学院大学，北京 100049；2.中国科学院光电研究院，北京 100094；3.中国测绘科学研究院，北京 100073)



基于浮动车数据的路口探测方法

谭 祥 爽1，王 静1，宋 现 锋1,2*，许 长 辉3，汪 超 亮2

(1.中国科学院大学，北京 100049；2.中国科学院光电研究院，北京 100094；3.中国测绘科学研究院，北京 100073)

路口及其通行规则探测是当前路网自动化提取工作中的难点问题，该文提出了一种简单高效的从浮动车数据中探测路口与转向规则的方法。假设车辆航迹线转弯密集区为路口，首先通过对转弯曲线空间聚类分析获得路口中心，再利用同心圆面积递增法估算出路口覆盖范围，最后根据路口范围内航迹线行驶方向分布模式，识别出通行规则。该方法的特点是将路口视为具有中心和半径的区域,而不是简单的点。将该方法应用于淮北市城区出租车采集的浮动车数据，同人工解译结果相比，探测路口的正确识别率约为91.6%，路口位置与解译结果平均距离为3.57 m，表明方法具有较高的实用价值。

浮动车数据;路口识别;转向规则;空间聚类;MeanShift算法

0 引言

电子地图在交通管理、车辆导航、城市规划等方面发挥着至关重要的作用[1]。但是，当前电子地图的生产仍然是一个比较耗时费力的工作，尤其是含交通规则的可支持车辆导航和路径规划的路网，需要配备GNSS差分站等专门设备进行外业测量和室内手工编辑方能成图[2]。当前出租车等公共车辆均配备了车载GNSS，在车辆安全监测的同时记录了大量的行车航迹数据。这类低定位精度的海量浮动车数据能够及时捕捉道路及其特征变化[3]，被认为是一种低成本、高效率的道路制图新数据源，受到了国内外学者的关注。

交通路网是电子地图的主体，是由路口和道路构成的具有拓扑关系的网络结构。其中，路口是连接道路的交通枢纽，覆盖一个局部空间区域，包含各种通行规则，控制着车辆在不同道路之间的有序通行。高质量导航交通地图的构建，对路口的覆盖范围定位与通行规则的判断必不可少。

鉴于路口的复杂结构，目前大部分学者通过提取道路，将路段交点视为路口，由此得到的路口是一个简单的点，并非空间区域。例如：Lima和Ferreira 先栅格化航迹点覆盖区域，再细化栅格区域方法构建道路网，同时将路段交叉点当作路口[4]。Cao和Krumm建立了一种新型的力学模型，将位置和方向相似的点聚类形成具有车道信息的路网，提出利用模式识别的方法判断路口[5]。Bruntrup等先初始化道路网络为空集，然后采用人工智能算法判断航迹点与已有道路的空间关系，将GPS航迹逐条加入路网，也是将交叉点当作路口[6]。随着研究深入，部分学者提出了可以获取路口空间范围的方法，但仍然缺少通行规则的判断，使得路网的导航性受到限制。Fathi等首先选择代表性路口区的航迹数据作为训练样本，然后通过待判定位置的GPS航迹线空间分布模式和训练样本的相似性来判断其是否为路口[7]。Schroedl等通过分段、聚类等方法推断出车道中心线的位置，再借助商业地图和车道中心线判断路口区域位置[8]。

因此，在目前提取路网和路口工作中，尚无法自动提取路口结构和通行规则等信息，构建出与实际路网相符的拓扑关系，实地测量和人工干预编辑仍然是当前交通路网制图的主要方式。为了弥补以上方法的不足，本文充分利用浮动车数据的特点，不仅探测路口位置和路口分布范围，而且提取路口的通行规则，探索路口提取的自动化方法，为支持构建高质量的车辆导航地图奠定基础。

1 路口探测原理

车辆转弯起始(调头)到转弯(调头)结束的航迹线段称为转弯曲线。车载GNSS航迹线的转弯曲线和路口位置存在着很强的关联性。从统计角度看，车载GNSS转弯曲线发生在路口处的概率远高于发生在直行道路的概率。

图1a中灰色线段是从大量车载GNSS航迹线上提取的转弯线段，图1b从三维角度展现了路口区与非路口区曲线密度的差异。结果表明转弯曲线空间分布密度在路口区和非路口区具有显著差异：路口区异常密集、道路区分散稀疏。

图1 车载GNSS转弯曲线分布

Fig.1 Vehicle GNSS turning curves

基于路口与转弯曲线的分布关系，本文提出假设：转弯曲线分布密集的地区为路口。在此基础上构建一种基于车载GNSS航迹线的路口自动提取方法。路口的探测分为3步：位置的探测、路口范围探测和内部通行规则探测。通行规则是指路口允许的通行方式。例如，路口的某一方向驶入车辆只允许直行，不允许左转。技术路线如下：首先提取航迹线的转弯曲线并生成密度格网，统计各单元格中转弯曲线分布密度；然后基于密度聚类方法[9-12]将转弯曲线密度高的区域识别为路口区并计算出路口的中心位置；在路口位置的基础上利用同心圆递增法计算出路口覆盖半径；最后对覆盖半径内的行车轨迹的转向进行聚类分类，分析出路口内的通车规则。

2 路口识别方法

2.1 转弯曲线的空间密度估算

通常车辆在一条航迹线中，位于转弯和掉头处航迹点的平均曲率较大，而平直道路上航迹点的平均曲率较小甚至为0。根据曲率的变化可提取出位于车辆航迹线的转弯线段部分。

采用网格将城区覆盖范围格网化，统计位于每个单元格内的弯曲航迹曲线的数目，计算网格密度值作为网格的属性值。筛选线密度值大于0的单元用于路口探测，简称路口栅格点。

本文路口探测方法属于点密度聚类分析类型，通过搜索密度峰值区域发现路口。路口区域内单元格值越高，路口越易被探测到。实际上，单元格过小，栅格数据量会急剧增加；过大则探测的路口位置准确性会大幅下降。通过设计一组网格划分与密度计算实验，比较了3个样本路口在不同单元格大小下的最高密度值分布，本文确定了适合该组数据集的网格经验值为5 m。

通常情况下，道路区内栅格点的属性值非常低，而路口区相对较高，尤其是位于路口中心位置的密度值常为局部区域的高值点。统计整个地区栅格点的密度值分布，其近似符合泊松分布，考虑置信度为0.95的置信区间，假设小于置信区间下限的栅格点属于路口的可能性很小(道路区非法掉头、随机转弯等情况)，选择大于置信区间下限的栅格，从而将路口区域的高密度值网格点提取出来用于路口探测分析。

2.2 基于密度聚类方法的路口探测

对筛选出的栅格点进行空间聚类，可有效探测出各路口及其中心位置。MeanShift算法[9]通过概率密度梯度函数估计离散点在各空间维的偏移均值来更新位置，通过不断迭代使得离散点移动到局部高密度值区。MeanShift定义了一组核函数，确保离散点与当前聚类中心点的距离不同，其对新聚类中心偏移向量的贡献亦不同。此外，笔者以栅格点的密度值作为权重系数，从而使得不同栅格点在决定路口中心位置时的重要性不同，其公式如下所示，本文中采用高斯核函数。

高斯核函数：

K(xi-x)=e-c||xi-x||2

(1)

路口中心位置：

(2)

式中:x为路口中心的初始位置，m(x)为x的新位置，N(x)为点x的邻居集合，xi为路口区的第i个栅格点的位置，w(xi)为第i个栅格点的密度值(权重值)。

路口探测过程中需要给出聚类搜索半径。若聚类半径过大，则会将距离较近路口合并；若聚类半径太小，则又可能将较大路口探测为多个路口。因此，本文采用雷普利函数分析聚合效果，给出了一个经验值分布范围，搜索半径15～30m。其中，最优搜索半径25m的聚合效果最好。

2.3 路口半径确定

通常，路口形状较为复杂，本文采用圆形近似代替，路口大小用覆盖路口的圆形半径表示。栅格点呈簇状不均匀地分布在路口物理区域和功能区，栅格密度值呈现从路口中心向外围逐渐递减的趋势。

本文提出了一种同心圆递增法来探测路口的覆盖半径。该方法以聚类中心为圆心逐步增大探测半径，以同心圆圆环内栅格密度平均值与同心圆内圆栅格密度平均值的比值z为指标(理论上z位于0～1之间)，判断当前外圆半径是否为最佳半径。具体步骤如下：1)以探测出的路口位置为圆心，以初始半径(如5m)确定圆，计算圆内栅格密度平均值；2)以一定增量增加圆半径(如1m)，计算z值；3)循环步骤2直到圆半径达到预定值或者z接近0时终止循环。

分析z值变化规律(图2)，可将路口区域附近栅格点分为内核区、边缘区和道路区。在路口内核区，z波动接近数值1，说明内核区内密度变化不大。路口边缘区内z逐渐降低说明此区域逐步偏离路口。在靠近道路区，z在0值附近波动，表示已离开路口区。

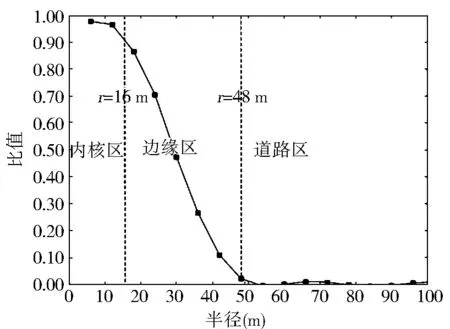
图2 基于同心圆递增法的路口半径探测

Fig.2Determiningtheradiusofanintersectionbytheconcentricareaincrementmethod

在路口内核区和边缘区交界处，z值发生急剧下降，实验中将该位置所对应的半径数值定为路口覆盖区的半径(图3)(见封3)。由于航迹线定位误差原因，探测的半径值较实际路口偏大，但是可以确保对转弯航迹线的完整切割，用于路口通行规则分析。

2.4 路口通行规则的识别

在城市中，为了缓解交通压力，路口会设置通行规则，禁止某些转向，避免引起交通阻塞，提取路口通行规则对构建路网准确的拓扑关系至关重要。

基于探测的路口及其范围，裁剪路口处的行车轨迹线，采用层次聚类对这些轨迹线的驶入和驶出方向进行聚类，将相同驶入和驶出路口方向的航迹线分为同一类。典型路口的转弯分类结果如图4所示(见封3)，路口行车轨迹被分成不同类别，计算每一类别所有轨迹驶入和驶出方向的平均值，以获得通行规则，如(2°，87°)表示由南向北驶入路口，右转弯驶向东方。这些通行规则是路网拓扑、路径规划和车辆导航的基础信息。同时，利用这些规则及其类别数目还可进一步从探测的路口中甄别出道路急转弯。

3 实验结果与讨论

3.1 研究区

实验区位于安徽省淮北市城区，其中路口以平面交叉口为主，有丁字、十字、环岛等类型。实验数据来源于出租车车载GNSS记录仪，数据采集频率为1s，定位精度为5～15m。每条数据记录了采集时间、经度、纬度、行驶速度和方向角等信息。本文数据集包含了从2011年6月到2013年1月的215万条航迹点记录，覆盖了整个淮北市区的交通道路。

3.2 路口探测结果

本方法采用Python和SciPY软件包，实现了路口自动探测程序。图5将路口提取结果同遥感影像叠加，同人工解译结果对比，路口结果较好。

图5 淮北市区路口提取结果

Fig.5DetectedintersectionsbasedonfloatingcardatainHuaibeiCity

实验数据覆盖淮北市区交通路口462个。采用本方法探测到437个路口，其中非路口地区错判成路口为14个，正确路口为423个，共遗漏39个路口，路口正确识别率约为91.6%，探测路口位置与解译结果平均距离为3.57m。从实验结果看，本文方法具有较高的实用价值。

错判路口主要发生于城市的大型环岛路口处，由于环形路口覆盖范围较大，并且路口中心区域没有航迹覆盖，在MeanShift聚类过程中无法找到环形路口中心，迭代最后终止在圆环与路段的连接处。结合探测的路口半径和环岛(或环形)路口的特点通过GIS空间叠置分析，将邻近的错判路口合并。未能探测出的路口主要发生在立交桥区和航迹线极其稀疏处(如：城市南部或小支路区)。立交桥覆盖区域大、匝道转弯平缓，局部范围内所经过的航迹线曲率较小，导致立交桥部分路口不能被识别。

3.3 通行规则结果分析

路口通行规则是基于对路口范围内的航迹数据分类进行提取的。路口每一个允许的通行方式都存在着大量轨迹线，统计这些轨迹线不仅获得了某通行规则允许驶入路口和驶出路口的方向，而且航迹线的数目以及时段分布还可以提示路口各方向之间交通压力的相对大小。图6(见封3)是淮北市的一个交叉口，该路口轨迹线分为8类，分别用不同颜色表示。根据规则可以看出，南北走向的路是单行车道，路口东侧允许掉头。表1是一个路口通行规则及其对应的航迹线统计数目结果。

表1 通行规则提取结果

Table1Trafficrules

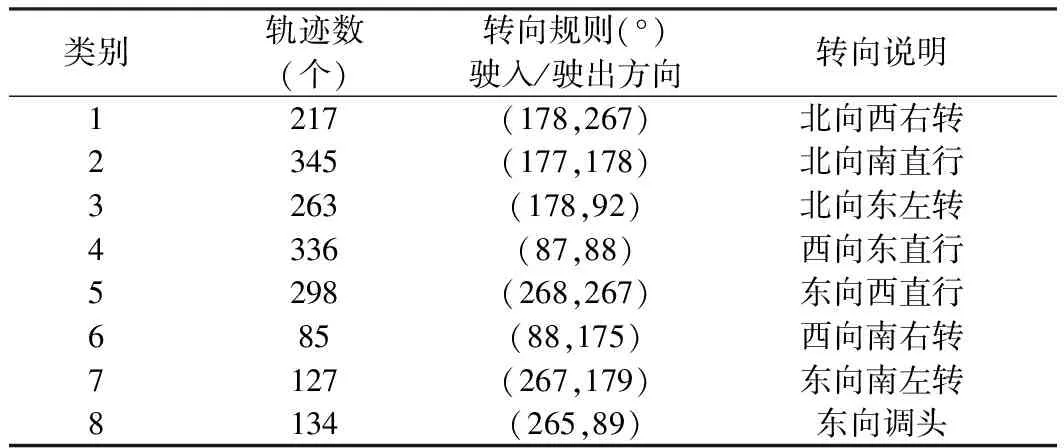
类别轨迹数(个)转向规则(°)驶入/驶出方向转向说明1217(178，267)北向西右转2345(177，178)北向南直行3263(178，92)北向东左转4336(87，88)西向东直行5298(268，267)东向西直行685(88，175)西向南右转7127(267，179)东向南左转8134(265，89)东向调头

3.4 聚类方法选择

本文采用了聚类分析的路口探测方式，结合海量航迹数据特点，对聚类方法有以下要求：1)路口数目未知，即聚类方法要求输入的参数中不应该包含聚类数目；2)栅格间的空间距离与栅格值(转弯曲线密度值)对聚类结果影响都较大，在聚类过程中必须予以考虑。根据以上条件， MeanShift、DBSCAN两种聚类方法都比较适用。

Meanshift 算法是一个迭代过程，直至找到概率密度函数局部最大值结束。DBSCAN算法是将具有足够高密度的区域划分为一类，要求类中的每个点在给定的半径范围内至少包含一定数目的点[13]。Meanshift聚类算法只需要指定一个搜索半径作为参数，DBSCAN聚类算法需要搜索半径和聚类最小规模阈值。DBSCAN对最小规模阈值比较敏感，阈值过小将会切割大路口，过大又会合并邻近的路口，应用于本工作时结果波动大。Meanshift聚类则可以较好地解决这一问题，其迭代寻找局部密度的高值点，密度不同的地区相互间不受干扰。

表2是两种聚类方法在结果和时间性能上的对比，从计算效率上看，DBSCAN聚类方法比Meanshif方法耗时长，但是仍然在可接受范围内。从效果上分析，两种算法探测出的路口数目都少于人工解译的462个，但是MeanShift的正确识别率较高。

表2 聚类效果及效率对比

Table 2 Comparison of intersections detecting result and computational time of different cluster methods

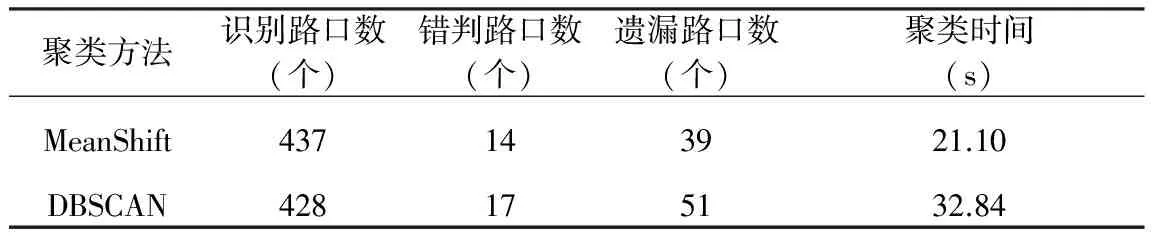
聚类方法识别路口数(个)错判路口数(个)遗漏路口数(个)聚类时间(s)MeanShift437143921．10DBSCAN428175132．84

图7(见封3)显示了两个栅格相连的路口，栅格中存在两个密度高值区，中间存在着密度较小的栅格点(噪音点)。MeanShift算法将每个栅格点都选作种子起点寻找路口中心，栅格点不断从外围向路口中心移动，各点逐渐汇拢，如图7a中绿色线条所示的移动轨迹，最后分别汇集至两个密度高值区，形成两个路口中心。DBSCAN是寻找密度符合要求的点的最大集合，图7b 是在聚类最小规模阈值偏小时得出的结果，每个点都符合要求，所有栅格点被归为一类。由于数据中存在多处两个相邻路口被噪音栅格相连的情况，很难选择一个统一的域值，最终导致DBSCAN得到的结果比MeanShift遗漏的路口多。

4 结论

本文提出了一种利用浮动车数据探测路口的方法。不同于以前的方法，本文获取的路口是有中心和半径大小并且含内部通行规则的区域。基于该方法分析了车辆航迹数线在路口处的曲率与航向变化特点，采用Meanshift聚类算法探测路口中心，同时用提出的同心圆递增法确定了路口半径，这一信息有助于路口等级划分与规模比较。更为重要的是，路口区域内不同航向的航迹线代表了不同的通行规则，通过航迹线的转向分类，提取出了路口通行规则。最后，利用在淮北市出租车采集的GNSS航迹线数据进行了实验，结果表明本方法在探测平面路口方面取得了较好的效果，正确识别率约为91.6%。后续工作还需要对该算法进一步改进，对大型环形路口和立交桥区路口的探测进行深入探索。

[1] 谢振东.智能交通系统的发展与思考[J].广州交通， 2001(2)：32-36.

[2] LI J,QIN Q M,XIE C,et al.Integrated use of spatial and semantic relationships for extracting road networks from floating car data[J].International Journal of Applied Earth Observation and Geoinformation,2012,19:238-247.

[3] EKPENYONG F,PALMER-BROWN D,BRIMICOMBE A.Extracting road information from recorded GPS data using snap-drift neural network[J].Neurocomputing,2009,73(1-3):24-36.

[4] LIMA F,FERREIRA M.Mining spatial data from GPS traces for automatic road network extraction[A].6th International Symposium on Mobile Mapping Technology[C].Presidente Prudente,S o Paulo,Brazil,2009.

[5] CAO L,KRUMM J.From GPS traces to a routable road map[A].17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (ACM SIGSPAITLA GIS 2009)[C].ACM:Seattle,WA USA.2009.3-12.

[6] BRUNTRUP R,EDELKAMP S,JABBAR S,et al.Incremental map generation with GPS traces[A].Proceedings of the 8th International IEEE Conference on Intelligent Transportation Systems[C].Vienna,Austria,2005.

[7] FATHI A,KRUMM J.Detecting road intersections from GPS traces[A].GIScience 2010,Sixth International Conference on Geographic Information Science[C].Zurich,2010.

[8] SCHROEDL S,WAGSTAFF K,ROGERS S,et al.Mining GPS traces for map refinement[J].Data Mining and Knowledge Discovery,2004,9(1):59-87.

[9] CHENG Y Z.Mean shift,mode seeking and clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence (IEEE),1995,17(8):790-799.

[10] ESTER M,KRIEGEL H P,SANDER J,et al.A density-based algorithm for discovering clusters in large spatial databases with noise[A].Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining[C].Portland,OR,AAAI Press,1996.226-231.

[11] COMANICIU D,MEER P.Mean shift:A robust approach toward feature space analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(5):603-619.

[12] ROSENBLATT M.Remarks on some nonparametric estimates of a density function[J].Annals of Mathematical Statistics,1956,27(3):832-837.

[13] 冯少荣，肖文俊.DBSCAN 聚类算法的研究与改进[J].中国矿业大学学报， 2008，37(1)：105-111.

Detection of Road Intersections Using Floating Car Data

TAN Xiang-shuang1，WANG Jing1，SONG Xian-feng1,2，XU Chang-hui3，WANG Chao-liang2

(1.UniversityofChineseAcademyofSciences，Beijing100049;2.AcademyofOpto-Electronics,ChineseAcademyofSciences，Beijing100094;3.ChineseAcademyofSurveyingandMapping，Beijing100073,China)

The detection of intersections is a hotspot and difficulty issue in the automated extraction of road network from floating car data (vehicle GNSS trajectories).This paper presents a simple but efficient approach for detecting intersections and associated turning rules.Assuming intersections are located in the areas where exists local maxima of dense turning curves of vehicles,the locations of intersection are first detected by the MeanShift algorithm,the sizes of intersections are then estimated by the proposed concentric area increment method,and the turning rules are finally determined by classifying the directions of both entrance and exit of those approaching trajectories.The advantage of this work is that an intersection is treated as a compact area in which traffic rules are used to schedule vehicles approaching,not a simplified point.This approach was tested using taxi trajectories collected in Huaibei City,China.In a comparison of visually interpreted results,more than 91.6% of intersection could be correctly recognized and the average distance between the result and the truth is 3.57 m.This shows a big potential advantage of applying the approach in generating routable maps.

floating car data;intersection recognition;turning rules;spatial clustering;MeanShift algorithm

2015-03-23；

2015-05-19

国家科技重大专项(2011ZX05039-004);中国科学院知识创新工程项目(KZCX2-EW-QN605);国家自然科学基金项目(40771167)。

谭祥爽(1987-)，男， 硕士，主要从事空间数据挖掘研究。*通讯作者E-mail：xfsong@ucas.ac.cn

10.3969/j.issn.1672-0504.2015.05.008

P283.7

A

1672-0504(2015)05-0034-05