应用CatMull-Rom样条曲线描述道路透视图中心线特征的方法研究
陈雨人,王瑞云,董永杰,贺思虹
(同济大学 交通运输工程学院,上海 201804)
应用CatMull-Rom样条曲线描述道路透视图中心线特征的方法研究
陈雨人,王瑞云,董永杰,贺思虹
(同济大学 交通运输工程学院,上海 201804)
采用三次 Bezier 曲线、三次B样条曲线和CatMull-Rom样条曲线分别拟合道路透视图中心线,并进行对比研究,分析了各自描述道路透视图中心线时控制点确定和拟合产生残差的情况,结果显示,在描述道路透视图中心线特征方面,CatMull-Rom样条曲线更为高效和精准,可以适应绝大部分道路几何设计形成的透视图中心线特征描述的需要。将道路透视图划分为“近景”、“中景”和“远景”3个不同功能区域,提出视曲线长和视曲率概念和相应的计算方法,将视曲线长和视曲率作为描述透视图中心线特征的形状参数,并结合运行车速进行了相关性分析。研究表明形状参数和运行车速密切相关。
道路工程;CatMull-Rom样条曲线;道路透视图中心线;视曲线长;视曲率
0 引 言
驾驶员眼中的透视图是由平纵横三方面线形组合在一起形成的,由驾驶员通过视觉进行观察并产生感知而形成认知,透视图形状在几何图形上更加复杂,且与平面图相比,能提供更多的曲率信息,或者说视觉中的透视图显示了比单纯平面或者纵断面更丰富的内容。我国道路设计规范认为透视图不仅可以用来判断平纵线形是否协调、道路与景观是否融合,而且小到超高缓和段的连接,大至构造物的设计,道路透视图几乎可以利用在道路几何设计的所有领域。其中起关键作用的是构成透视图轮廓的道路边线和中心线,尤其以中心线最具代表性,它提供了绝大部分的道路几何信息。从数学角度来看,中心线是由多段曲线组合而成,随着车辆的不断运动,这些多段曲线在驾驶员视野中持续发生变化,驾驶员正是从这些不断变化的多段曲线中获得操控车辆的重要信息,产生了期望车速和其他行为。如果这些被感知的信息和道路条件所能提供的相差比较大,就容易带来诸如运行车速和设计车速不一致、心理预期和实际供给不符合等问题,产生种种紧张和不舒适的感觉,研究表明:约有40%的道路交通事故是由于道路线形、路边环境或者两者之间配合不协调,从而引起驾驶员行车中产生错觉所造成的[1],可见透视图的研究对道路安全有着现实意义。
综上,对透视图中的中心线这种形态进行深入研究和应用就显得非常必要,其中一个重要内容就是需要使用合适的数学模型来表达它,国内外也有不少学者就道路透视图的表达模型进行了许多有价值的研究。L.Zakowska[2],T.Brummelaar[3],I.Taiganidis等[4]观察发现,道路曲线在驾驶员眼中的形状类似抛物线或者是双曲线,因此长期以来,用抛物线来拟合透视图中的曲线是一种比较常用的分析方法[5]。除此以外,还包括其他研究透视图的模型,比如:“双曲线模型”[6],“直线-抛物线模型”[7],改进的“双曲线模型”[8],“二次曲线模型”[9],“回旋曲线模型”[10]和“样条曲线模型”[11]等。
由于这些曲线基本上都属于二次曲线,因此一般只能描述存在一个拐点的形状,对于描述简单平曲线形成的透视图是合适的,但如果需要描述类似S曲线等形成的透视图就无能为力了。因此采用三次曲线描述道路透视图中心线更为恰当,可以描述更多种类型的道路线形,可以将拐点增加到2个,基本可以满足大部分情况下透视图中道路中心线描述的需要。在传统的图形学算法中,三次Bezier曲线、三次B样条曲线和Catmull-Rom曲线都属于连续可导的平滑曲线,应该都可以用来拟合道路透视中心线,但哪一个适应性、精准度和方便性会更好一些?
1 三种样条曲线的数学基础
1.1 样条曲线的数学描述
根据数学理论,三次Bezier曲线、三次B样条曲线和三次CatMull-Rom样条曲线都可以用统一的矩阵形式表示,如式(1):
(1)
式中:P1,P2,P3,P4为平面上4个控制点;M是基函数矩阵。
所谓的不同的样条曲线就是M矩阵的不同而已,根据有关数学定义,3种样条曲线逼近拟合道路透视图中心线情况如图1。
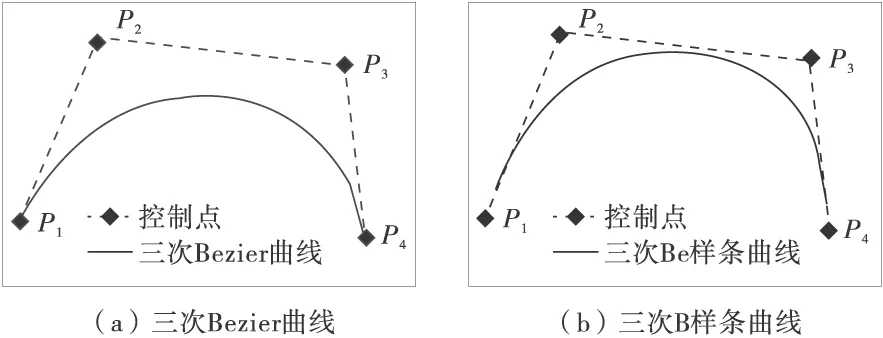
1.1.1 三次Bezier曲线
P(t)=(-t3+3t2-3t+1)P1+(3t3-6t2+
3t)P2+(-3t3+3t2)P3+t3P4
它由一组折线集或称之为Bezier特征多边形来定义,在端点处和对应的边相切,且样条曲线通过起点P1和终点P4,但不通过P2和P3点,最大的问题是不具有局部性,即修改4个控制点中的任何一个,整条曲线都会变化,也就是说插值运算时,需要P1,P2,P3和P4同时参与,属于整体内插,这在道路透视图研究中比较难以控制,如图1(a)。
1.1.2 三次B样条曲线
4)P2+(-3t3+3t2+3t+1)P3+t3P4]
这是一种特殊的Bezier曲线,也不通过控制点,但是具有局部性,即修改某一控制点时只对相邻前后控制点之间的曲线产生影响,而对曲线的其他部分没有影响,也就是说插值运算时,前半部分只需P1,P2和P3参与,后半部分只需P2,P3和P4参与,可以进行局部内插,如图1(b)。
1.1.3CatMull-Rom样条曲线
CatMull-Rom也是一种B样条曲线,但是其中Pt点处的切线与相邻前后两点连线平行,这就使得该曲线与前两种样条曲线最大的不同就是内插获得的曲线通过P1,P2,P3和P4,同时和三次B样条曲线一样具有局部性,即修改某一控制点时只对相邻前后控制点之间的曲线产生影响,而对曲线的其他部分没有影响。在插值运算时,前半部分只需P1,P2和P3参与,后半部分只需P2,P3和P4参与,可以进行局部内插,这在一些应用中是有意义的,如图1(c)。
1.2 应用样条曲线描述道路透视图中心线
图1(d)、(e)、(f)是分别用这3种样条曲线拟合道路透视图中心线及有关控制点的情况,可以看出虽然这3种样条曲线都可以逼近中心线,但是Bezier曲线和B样条曲线的控制点的位置仅仅控制了曲线的基本形状,道路中心线并不经过控制点,如果直接用于描述透视图中心线,难以控制插值后形成的中心线形态,而CatMull-Rom曲线与前两种样条曲线最大不同点在于内插获得的拟合曲线可以通过所有4个控制点,具有较强的适应性,这就使得该曲线在透视图中心线形态控制方面有重要的意义。此外Catmull-Rom样条曲线具有局部性,即修改某一控制点时只对相邻前后控制点之间的中心线产生影响,而对中心线的其他部分不会产生影响,所以无论从控制点位置和曲线拟合情况来看,Catmull-Rom样条曲线都明显要比其他两种样条曲线更适合用来描述透视图中心线,笔者将从拟合残差方面进一步分析。
2 不同样条曲线描述道路透视图中心线拟合残差分析
2.1 试验方案及采集的数据资料
通过选择不同等级道路建立虚拟环境,低等级道路采用成都一段农村道路,全长5 km,设计车速40 km/h;高等级道路采用广西一段高速道路,全长20 km,设计车速100 km/h。
考虑到笔者主要研究透视图中心线特征,故虚拟环境只做道路的简化模型,包含一根中心线和两侧的边线,不细化道路两侧的景观和建筑物。建立虚拟环境见图2;所需的透视参数由表1确定,表1也显示了试验中使用的模拟驾驶环境。每段道路要求8位试验者进行模拟驾驶,只有加速、减速的动作,不需要变换车道,也没有其他车辆存在,没有特殊要求,只需按照自己的期望驾驶,在这一过程中采集的数据资料为行驶速度和沿桩号方向每隔5 m生成的道路透视图中心线图像坐标集(xio,yio),可以保证每位试验者在同一桩号处获得是相同透视图信息,将8位试验者在同一桩号处的行驶速度进行简单数学平均,以该值作为该桩号处的运行车速V。
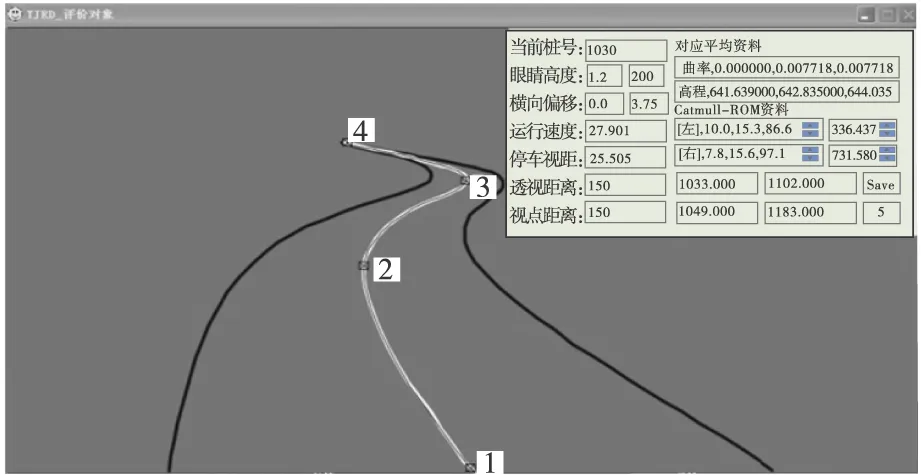
图2 模拟驾驶虚拟环境

表1 进行模拟驾驶的虚拟环境及透视参数
2.2 用样条曲线来拟合逼近道路透视图中心线的残差计算方法
以所获得的透视图中心线图像坐标(xio,yio)为基础,应用上述3类样条曲线来拟合逼近,根据道路透视图中心线的特点,在控制点P1,P2,P3和P4约束下,样条曲线可以最大程度地描绘出道路透视图的形态,根据最小二乘法,以拟合内插生成的曲线越逼近原来透视图中心线为越好,也就是以拟合精度的平均残差ω为最小为目标,其中ω根据式(2)计算确定。
案例教学法的主要目的是职业实践训练,即通过正确的职业导向引导学生掌握实用技能,起到事半功倍的教学效果,提高执业能力。医药职业岗位侧重实践能力,需要应用型人才,传统理论教学很难实现重应用、重素质的综合性人才的培养目标。借助真实案例所提供的问题,设立仿真的问题学习情境,让学生尽可能地处于真实的职业环境,体会和学习职业所需的临床思维和实用技能,从而激发学生的学习兴趣,培养自学能力、组织能力、表达能力、分析和解决问题能力、发散性思维能力和团队协作等多重能力。
(2)
式中:(xi,yi)为拟合获得的三次样条曲线特征点坐标;(xio,yio)为道路透视图中线上的特征点图像坐标;n为参与拟合的特征点数量。
这一过程由辅助程序来完成,对每段道路按照透视参数产生透视图,图中除表示两车道边线的粗线以外,在中心线位置产生连续的道路透视中心线,它的图像坐标(xio,yio)被记录下来,同时根据选定的样条函数,根据上面最小二乘原则,拟合产生一条透视中心线,同时计算出平均残差ω。
2.3 不同样条曲线拟合道路透视图中心线的残差分析
分别将三次Bezier曲线、三次 B样条曲线和CatMull-Rom样条曲线对应的拟合平均残差进行分析研究,总体均呈正态分布,说明拟合残差具有统计学的规律性和稳定性,如图3。
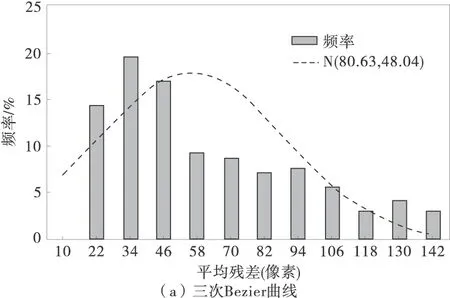
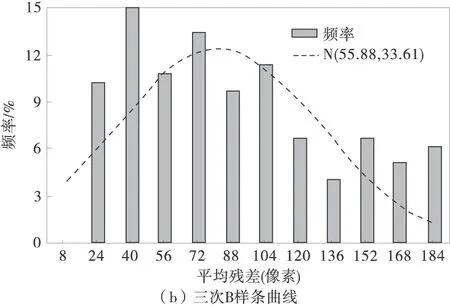
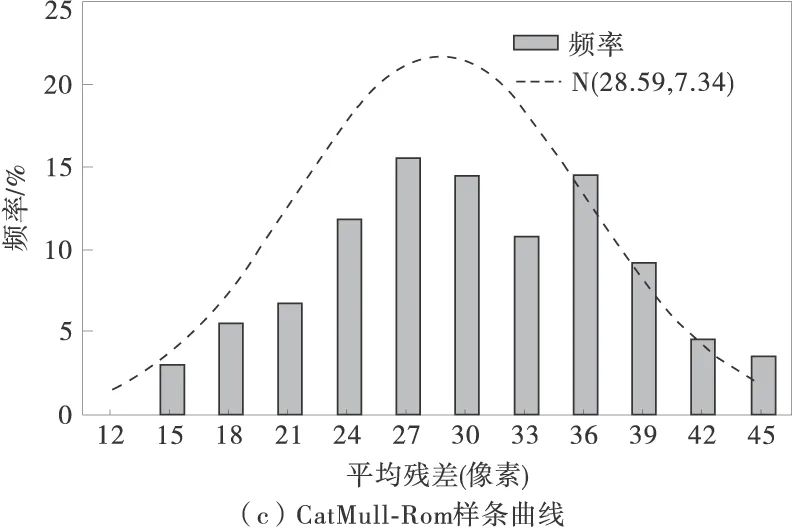
图3 三种样条曲线平均拟合残差的分布情况
其中三次Bezier曲线为N(80.63,48.04)的正态分布,残差的期望值为80.63(像素,以下同),为3种曲线里面最大的,而其标准差也达到了48.04,相对来说比较分散;三次B样条曲线为N(55.88,33.61)的正态分布,无论残差期望值,还是标准差都处于中间位置;而CatMull-Rom样条曲线所拟合的残差呈N(28.79,7.34)的正态分布,是3种样条曲线里面拟合残差最小的,期望值为28.79,标准差为7.34,整个残差分布形态比较匀称。
因此,选择CatMull-Rom样条曲线来描述道路透视图中心线是合适的。
2.4 应用CatMull-Rom样条曲线的描述多种道路线形情况
图4是使用CatMull-Rom样条曲线描述的多种道路线形情况,包括从高速道路到一般农村道路等不同等级,可以适应包括同向曲线、反向曲线、连续曲线等多种曲线组合的形态变化,控制点位置都可以精确计算出来。由此可以看出CatMull-Rom样条曲线可以满足绝大多数透视图形态描述的需要。

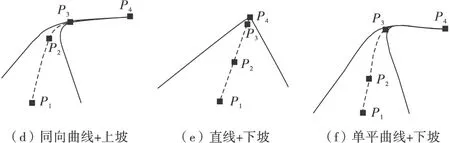




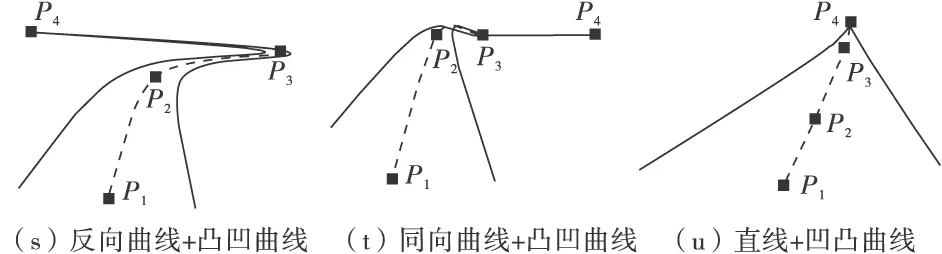

图4 CatMull-Rom样条曲线对几种道路透视图特征描述
3 基于CatMull-Rom样条曲线的道路透视图中心线计算模型研究
通过论述采用CatMull-Rom样条拟合道路透视图中心线是可行的,并且可以基于最小二乘原理确定4个控制点{P1,P2,P3,P4}位置信息,从数学角度来讲没有问题。因为这4个控制点一旦确定,其余所有点都可以通过式(1)内插出来;但从应用于道路几何设计有关研究角度来看,仅仅这样还无法解决问题,为此笔者进行了进一步的研究,提出透视图“近景”、“中景”和“远景”功能区概念,并设计了由视曲线长、视曲率组成的道路透视图中心线形状参数来描述透视图中心线形态特征情况。
3.1 基于CatMull-Rom样条曲线的道路透视图中心线计算模型
根据以上分析,笔者基于Catmull-Rom样条曲线建立道路透视图中心线计算模型,如图5。
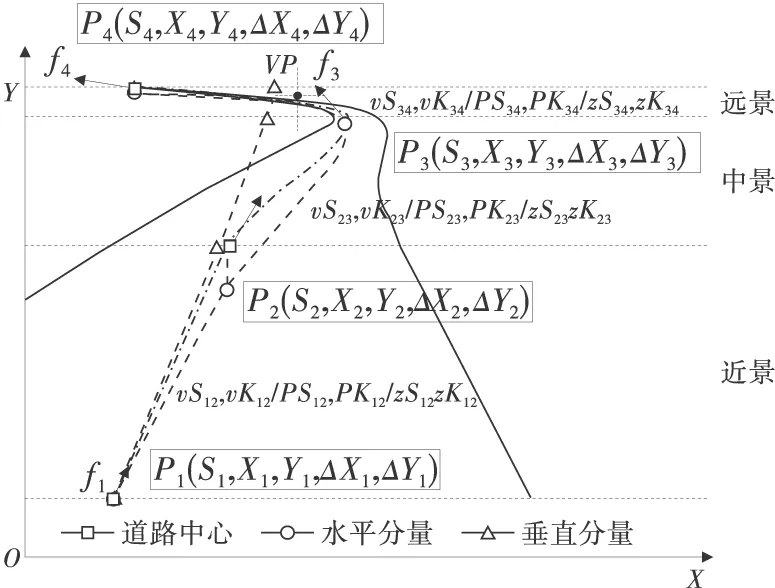
图5 基于CatMull-Rom样条曲线的道路透视图中心线计算模型
以驾驶员视野左下角为坐标原点建立坐标系统,X轴和Y轴的单位均为像素,道路中心线由n个有序点构成,其图像坐标集合为{xoj,yoj} (j=1,2,…,n,下同),而标为“水平分量”和“垂直分量”则为中心线在视平面和视垂面上的投影,都可以由(P1,P2,P3,P4)作为控制点的CatMull-Rom样条曲线来拟合。这4个控制点的信息用(Si,Xi,Yi,ΔXi,ΔYi)(i=1,2,3,4)表示。其中:Si为透视图中心线在该点累计的曲线长度(像素),文中称为视桩号;Xi,Yi则为图像坐标(像素);ΔXi,ΔYi则分别表示点Pi到视垂面和视平面在X方向和Y方向的偏离值(像素)。除此以外,每个控制点还有一个fi,表示过该点的透视图中心线的切线方向角(弧度)。
过控制点(P1,P2,P3,P4)的4条水平线将透视图在视域范围内分为3个不同的区域,笔者称为透视图的“近景”、“中景”和“远景”。这3个区域正常情况下长度大致相等,但由于平纵组合的不同,相互位置变化很大,图4显示了这种变化情况。显然,这些控制点位置和道路几何设计指标,尤其是平纵组合的方式关系是很密切的,从一个侧面也可以反映道路几何设计的情况,这3个区域在影响驾驶行为方面将发挥不同的作用。用[vSi(i+1),vKi(i+1)]、[pSi(i+1),pKi(i+1)]和[zSi(i+1),zKi(i+1)]描述3个区域内的透视图形态特征(视曲线长,视曲率),称为道路透视图中心线形状参数,表示透视图中心线在驾驶员眼中的长度和弯度的情况。VP为视线集中点。
3.2 透视图中心线形状参数的计算
vSi(i+1),vKi(i+1)作为描述“近景”、“中景”和“远景”这3个区域内透视图中心线形态的形状参数,具体计算方法如式(3):
(3)
式中:i=1,2,3;vSi(i+1)表示控制点Pi和P(i+1)之间的视曲线长;vKi(i+1)为该两点之间形成的视曲率,也就是切线方向角(弧度)的单位变化率,平面曲线左右转对驾驶员视觉感知来说是相同的,所以不考虑正负;fi和Si分别为透视图控制点Pi对应的切线方向角(弧度)和视桩号(像素)。
3.3 形状参数和运行车速的相关性分析
为分析形状参数在描述驾驶行为方面的有效性,笔者继续使用拟合残差模拟实验的数据进一步研究,分析形状参数vSi(i+1),vKi(i+1)和运行车速V之间的相关性,并绘制出相互关系图,如图6。

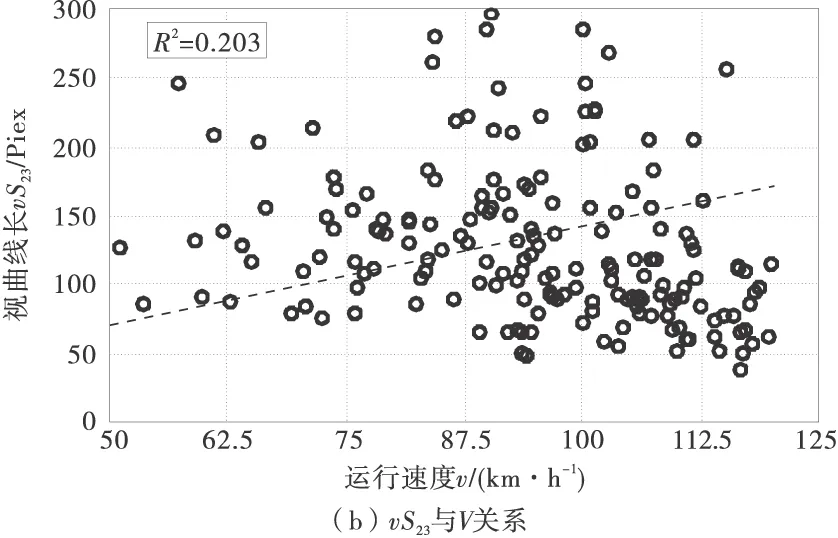

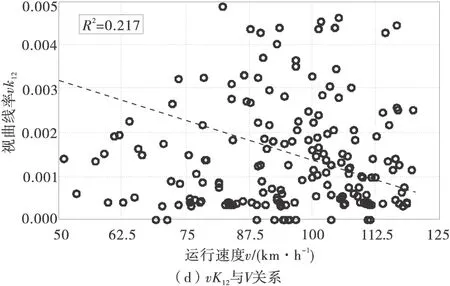
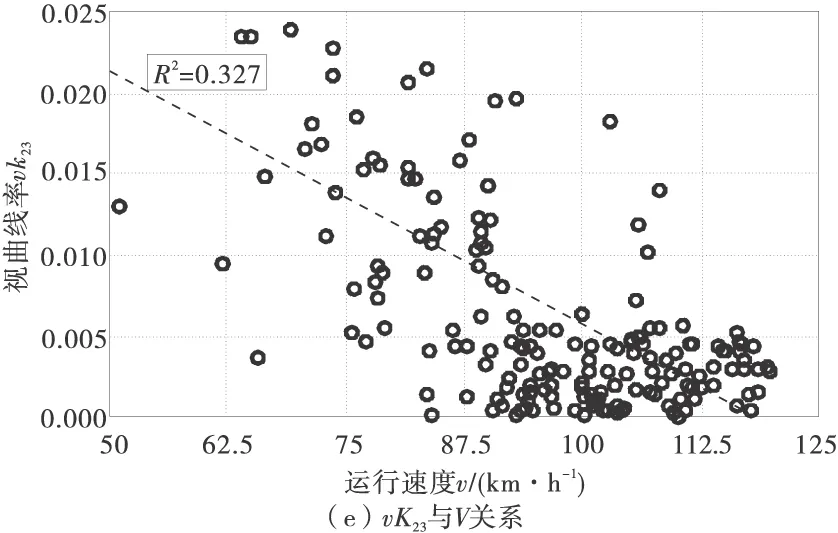

图6 形状参数与运行车速的相关性分析
从图6中可以看出,视曲线长度vSi(i+1)和运行车速V、视曲率vKi(i+1)和运行车速V都有一定的相关性。从相互关系来看,随着视曲线长度的增加,运行车速有增加的趋势,而随着视曲率的增加,运行车速呈下降的趋势,这说明驾驶员会根据所获得透视图中心线长度以及弯曲程度调节运行车速。从视曲线长度来看,“近景”和“远景”相关性相对“中景”高些,说明驾驶员在决定运行车速时受到近处和远处的透视图中心线长度影响比较大,事实上视距就和视曲线长度紧密联系在一起,尤其是“远景”处的视曲线长度,如果驾驶员感觉视距不够,自然会有所警觉,但往往驾驶员认为视距是足够的,但是实际道路条件并不能保证,这就提出了一个很重要的问题,如果由于平纵设计的缺陷(特别是平纵组合不当时),驾驶员视觉感知到的信息就可能和实际道路供给的条件相差比较大。再从视曲率来看,“中景”处的视曲率和运行车速相关性最大,“近景”处相关性略差,而“远景”处的相关性就非常低了,这说明驾驶员在行驶过程中,近处透视图中心线的弯度会对运行车速产生比较大的影响,这应该和驾驶员视线集中注视点的位置有关。驾驶员视野有中心视野和周边视野之分,各自发挥了不同的作用,“近景”和“中景”基本处于中心视野范围,对运行车速的影响就比较大,而“远景”位于驾驶员的周边视野内,其弯度影响运行车速的作用就比较弱。
因此,根据以上数据计算与分析,使用道路透视图中“近景”、“中景”和“远景”各自的形状参数“视曲线长vSi(i+1)”和“视曲率vKi(i+1)”来描述透视图的特征是可行的,可以有效地反映运行车速的变化,为深入应用道路透视图进行有关研究提供了可能。
4 应用研究分析
驾驶员主要通过视觉来获取道路信息,决策自己的驾驶行为,这里就存在着一个“道路对象”→“透视图”→“视觉信息形成”的认知过程,如图7。驾驶员眼中的透视图主要是由平纵线形结合横断面产生的三维映射,其核心是透视图上面的中心线,这一过程是由步骤(1)完成的,然后由驾驶员通过视觉感知并重构产生信息认知,这个过程由步骤(2)完成。由于平纵组合以及其他因素的影响,由步骤(2)感知重构获得的平纵信息和步骤(1)的原始平纵指标之间就会存在偏差,比如感知到的平曲线或者竖曲线信息就可能比实际设计的要大或者小,当这种偏差超过一定范围时,就会导致驾驶行为出现问题,比如最容易发生的情况就是运行车速和设计车速不吻合,相反,如果驾驶员所感知的信息和实际条件比较一致,意味着“需求”和“供给”之间保持平衡,则整个驾驶过程是连续舒适的,具备最高的安全度,此时的道路几何设计可以被认为处于最佳状态。

图7 驾驶员对道路几何信息的视觉认知过程
4.1 应用于道路平纵设计协调性评价的思路
道路几何设计的一个基本要求就是要满足平纵协调的要求,设计车速大于60 km/h时要进行组合设计,尤其是对于平曲线半径小于2 000 m,竖曲线半径小于15 000 m时,平纵组合显得更为重要。
现有的研究已经充分表明,不利的平纵组合容易导致对平面/纵断面信息感知出现偏差,特别是平面方面更是如此,由于透视的影响,驾驶员会把平曲线感觉更平坦了或者更尖锐了,把纵坡感觉更陡了或者更缓了。而目前检查平纵协调的方法基本上就是“平包竖”,尽量使得平曲线中点和竖曲线中点对应起来,在实际应用中不仅难以量化,而且效果也不好,现在基于笔者研究的道路透视图中心线计算模型将可以很好地解决这个问题。图8是应用于道路平纵设计协调性的基本流程,首先使用笔者研究的方法建立道路透视图中心线计算模型,获得透视图形状参数的“水平分量”和“垂直分量”,然后通过逆透视变换技术计算出驾驶员通过透视图所感知到的水平/垂直曲率的大小,最后将驾驶员感知到的水平/垂直曲率和道路几何设计实际的平曲率/竖曲率进行比较,如果感知的和设计的比较一致,就说明平纵组合带来的影响比较小,驾驶员基本可以通过视觉重构获得准确的信息,而如果两者之间差别比较大,就说明平纵组合已经影响到驾驶员对几何信息的准确感知,就可能存在潜在的安全隐患,使得驾驶行为出现偏差。

图8 道路平纵设计协调性评价流程
Fig.8 Road design evaluation process about horizontaland vertical coordination
4.2 应用于道路几何设计一致性评价的思路
道路几何设计的另一个基本要求就是要满足设计一致性的要求,为了解决这一问题,道路安全审计应运而生。道路安全审计通过评价道路设计一致性来达到优化道路设计,减少甚至避免交通事故发生的目的。道路设计的一致性从狭义上来看就是指道路线形设计与驾驶员的期望驾驶相适应的特性,从广义上讲是道路各设计要素的改变应该与驾驶行为相匹配。道路设计一致性也逐渐成为研究的重点,为提高道路设计的一致性,提出了基于运行速度的路线设计方法[12],目前对设计一致性的评价方法也越来越多,主要分为4种方法,分别是基于运行车速、基于车辆稳定性、基于道路线形和基于驾驶员工作负荷的评价方法。上述方法中都有一个共同的缺陷,那就是没有从驾驶员期望驾驶的角度出发,尤其是未从驾驶员视觉期望方面进行研究。事实上,道路设计一致性从本质上讲是道路设计应该符合并且适应驾驶员的期望要求。应用笔者研究的道路透视图中心线计算模型,同样可以比较好地解决这个问题,相比以往研究更具准确性和适应性。图9是应用于道路几何设计一致性评价的基本流程,通过采集评价位置前后共计5幅关键帧的透视图资料,计算出驾驶员通过视觉感知重构所获得的水平/垂直信息,然后分为两个部分进行评价,首先是和道路几何设计资料进行对比,分析驾驶员感知的几何信息与设计提供之间存在的偏差,然后再比较5幅特征位置处驾驶员感知重构获得的情况,这样可以分析前后路段之间驾驶员对几何信息感知存在偏差的情况。通过上述两个步骤的分析,可以有效地检验出设计缺乏一致性的情况。

图9 道路几何设计一致性评价流程
5 结 语
笔者主要研究了表达道路透视图中心线形态的计算方法,目的是为了对道路透视图或者驾驶员通过视觉获得的道路场景进行深入应用,解决目前存在的研究困难,推动相关领域内研究水平的发展。在此基础上,提出了针对道路几何设计中平纵协调性评价和几何设计一致性评价的详细流程,在下一步研究中将针对上述两方面的评价过程进行深入应用研究,标定相关阈值,建立一套完整的评价方法。对新建道路和已建道路,分别以虚拟透视图和通过视频技术获取的驾驶员视觉场景作为评价对象,均可以对其进行有效的评价和应用。
[1] 郭迁,吴国雄,王福建.道路线形及路边环境引起的错觉动画模拟分析[J].重庆交通学院学报,2006,25(5):40-44.
Gu Qian,Wu Guoxiong,Wang Fujian.The animation simulation analysis of the illusion caused by road alignment and roadside environment [J].Journal of Chongqing Jiaotong University,2006,25(5):40-44.
[2] Zakowska L.Road curve evaluation based on road view perception study [J].Transportation Research Record:Journal of the Transportation Research Board,1999,1689(1):68-72.
[3] Brummelaar T.The reversal point in the perspective road picture [J].Road Research,1983,13(2):123-127.
[4] Taiganidis I,Kanellaidis G.Approximate perspective design of roads [J].Journal of Transportation Engineering,1999,125(4):314-323.
[5] Kluge K.Extracting road curvature and orientation from image edge points without perceptual grouping into features[C]// Proceedings of the Intelligent Vehicles 1994 Symposium.[S.l.]:IEEE,1994:109-114.
[6] Khalifa O O,Khan I M,Assidiq A A M,et al.A hyperbola-pair based lane detection system for vehicle guidance[C]// Proceedings of World Congress on Engineering and Computer Science.San Francisco:IAENG,2010:585-588.
[7] Jung C R,Kelber C R.An improved linear-parabolic model for lane following and curve detection[C]// 25thSIBGRAPI Conference on Graphics,Patterns and Image.Natal,Rio Grande do Norte,Brazil,2005:131-138.
[8] Wang Jianwen,An Xiangjing.A multi-step curved lane detection algorithm based on hyperbola-pair model[C]// Hong Kong and Macau:2010 IEEE International Conference on Automation and Logistics (ICAL),2010:132-137.
[9] 周欣,黄席樾,刘涛,等.高速公路分道线识别与重建[J].重庆大学学报,2003,26(8):52-55. Zhou Xin,Huang Xiyue,Liu Tao,et al.Recognition and reconstruction for highway lane line [J].Journal of Chongqing University,2003,26(8):52-55.
[10] Loose H,Franke U,Stiller C.Kalman particle filter for lane recognition on rural roads[C]//2009 IEEE,Intelligent Vehicles Symposium.Xi’an:[s.n.],2009:60-65.
[11] Wang Y,Shen D G,Teoh E K.Lane detection using spline model [J].Pattern Recognition Letters,2000,21 (8):677-689.
[12] 张春笋,吴进良.基于运行速度的路线设计方法[J].重庆交通大学学报:自然科学版,2008,27(4):552-554. Zhang Chunsun,Wu Jinliang.Discussion on highway alignment design method based on operating speed [J].Journal of Chongqing Jiaotong University:Natural Science,2008,27(4):552-554.
Methods about Using CatMull-Rom Spline to Describe Characteristics ofRoad Centerline in Perspective View
Chen Yuren, Wang Ruiyun, Dong Yongjie, He Sihong
(School of Traffic Engineering, Tongji University, Shanghai 201804, China)
Cubic Bezier spline, cubic B-spline and CatMull-Rom spline were used to fit road centerline in perspective view in this paper. The control points and fitting residuals from the three kinds of splines were analyzed by comparative studies. The results show that CatMull-Rom spline is more efficient and precise than the others in describing road centerline features in perspective view. It can meet the needs of describing features of perspective view from the vast maiority of road geometric design. The perspective view is divided into “near-scene”, “middle scene” and “far scene” as three different functional regions, and the concept and calculation method of the visual curve length and the visual curve curvature were proposed as shape parameters of road centerline in perspective view, combined the correlation analysis with operating speed. The shape parameters and operating speed are closely related.
road engineering; CatMull-Rom spline; road centerline in perspective view; the visual curve length; the visual curve curvature
10.3969/j.issn.1674-0696.2015.04.08
2014-04-24;
2014-07-08
国家自然科学基金项目(51078270, 51238008);高等学校博士学科点专项科研基金项目(20120072110019)
陈雨人(1966—),男,江苏大丰人,教授,博士,主要从事道路交通规划设计、交通安全与道路环境、道路交通计算机辅助工程方面的研究。E-mail: Chenyr@tongji.edu.cn。
U491.254
A
1674-0696(2015)04-045-07

