预应力组合梁结构试验研究与剪滞效应分析

胡少伟，喻 江,2，谢建锋，徐爱卿

(1. 南京水利科学研究院，江苏 南京210024；2. 河海大学 土木与交通学院，江苏 南京 210098；3. 河海大学 力学与材料学院，江苏 南京 210098)



预应力组合梁结构试验研究与剪滞效应分析

胡少伟1，喻 江1,2，谢建锋1，徐爱卿3

(1. 南京水利科学研究院，江苏 南京210024；2. 河海大学 土木与交通学院，江苏 南京 210098；3. 河海大学 力学与材料学院，江苏 南京 210098)

为了深入分析剪滞效应对预应力钢-混凝土组合梁结构的影响，提出了一种新型的宽翼缘双箱钢-混凝土组合梁结构并进行试验研究，探讨了该结构在跨中集中荷载作用下组合梁的应力、应变，及挠度随荷载变化的特征。基于最小势能原理，并假定翘曲位移形函数，建立控制微分方程组，推导出了考虑剪滞效应、预应力增量作用下的应变及挠度函数表达式。结合算例，在线弹性范围内，对该组合梁结构进行了剪滞效应对比分析，结果表明：其误差在15%以内。

桥梁工程；双箱钢-混凝土组合梁；剪滞效应；预应力增量；解析解

0 引 言

紧跟蓬勃发展的交通事业和日新月异的城市化脚步，钢-混凝土组合梁作为继钢筋混凝土结构和钢结构之后一种新型结构，已经愈来愈多的被应用到桥梁工程、工业厂房、高层建筑，以及水利工程的设计和建造领域[1]。伴随着钢-混凝土组合梁的研究，该种结构经历了“I”型钢-混凝土组合梁、“T”型钢-混凝土组合梁、单箱型钢-混凝土组合梁等形式[2]。为了满足现代化交通的需要，大跨度、大宽度、高标准的桥梁正在被逐渐运用。大量工程实践表明，不论是组合梁结构，还是非组合梁结构，随着翼缘板的加宽，都会导致结构发生翘曲变形而破坏。究其原因，是由于板内剪切变形的影响，导致了正应力分布不均，使得梁在受弯时远离组合结构部位的翼板纵向位移滞后于组合结构部位，即发生了“剪滞效应”[3-4]。基于此，一种宽翼缘的双箱钢-混凝土组合梁结构被提出并被研究。

张元海等[5]运用变分法对考虑剪滞效应的宽翼缘“T”型薄壁梁进行了数值分析；基于能量原理，Guo Jian[6],Zhou Wangbao[7]等对单箱型组合梁结构建立了考虑剪滞效应的控制微分方程组，并通过推导运算求得了其相应的解析解；孙飞飞等[8]通过引入非均匀分布的纵向位移翘曲形函数, 建立了一个考虑滑移、剪力滞后和剪切变形的“I”型钢-混凝土组合梁模型，并推导出了均布荷载作用下的解析解；张元海等[9]提出了一种梁段有限元数值分析方法，对考虑剪滞变形时箱型梁进行了广义力矩法数值计算；胡少伟等[10]根据组合梁翼板微元的变形协调条件和平衡微分方程，建立了考虑剪滞效应的宽翼缘双箱组合梁应力微分方程求得其解析解，并结合试验加以分析。上述研究主要从理论分析着手，对“I”型截面、“T”型截面，以及单箱型截面钢梁及钢-混凝土组合梁进行了剪滞效应研究，分别运用变分法、能量守恒等基本原理，进行了理论推导分析和数值计算，求得不同约束条件、不同荷载作用下的解析解。

在国内、外学者研究的基础上，笔者提出了一种新型的宽翼缘双箱钢-混凝土组合梁结构，通过开展试验研究，分析了在初始预应力及预应力增量作用下，其结构的挠度变形特征、应变特征等参量。并根据结构受力及变形特点，假定翘曲位移形函数，基于最小势能原理，建立控制微分方程组，求得考虑剪滞效应、预应力增量作用下的应变函数表达式及挠度表达式。以试验设计试件为算例，在线弹性范围内，对该组合梁结构进行了剪滞效应对比分析。

1 试验概况

1.1 模型梁设计

依据GB 50017—2003《钢结构设计规范》和GB 50010—2010《混凝土结构设计规范》，双箱钢梁采用Q235-B碳素结构钢，并通过6 mm电弧焊焊接而成，混凝土翼板采用商品高强混凝土，强度等级C60。混凝土翼板和钢梁之间的剪力传递通过在钢梁托板上均匀焊接圆柱头栓钉来完成。混凝土翼板内布置构造钢筋，纵筋采用HPB235φ10，分为2层，每层5根；箍筋采用热轧圆盘条HPB235φ8@200，布置形式为四肢箍筋布置。为了完成预应力的施加，分别在组合梁端部设置加载块和底部设置转向块。模型梁参数见表1，具体构造如图1。

表1 模型梁参数

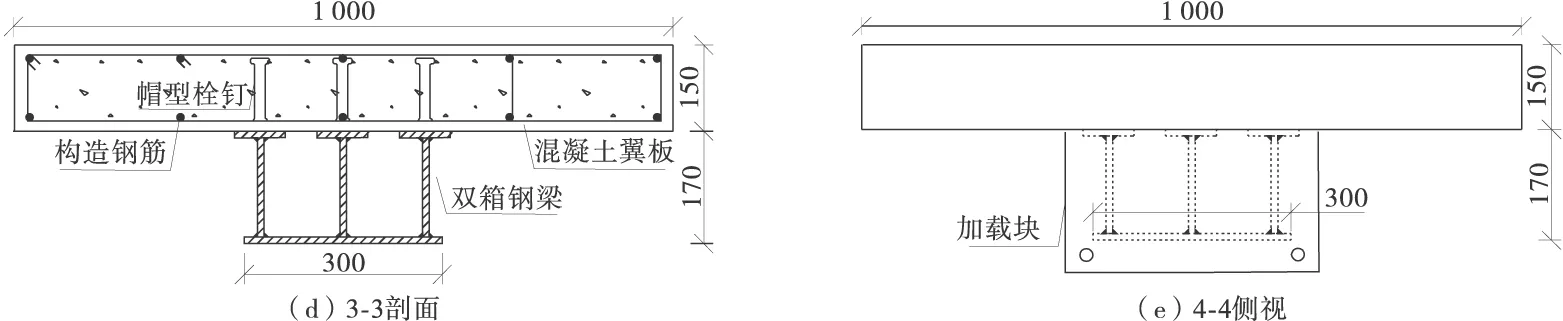
图1 组合梁模型构造

1.2 试验装置及测点布置

为了深入探测剪滞效应对组合梁混凝土翼板、钢梁底板、腹板的影响，根据结构的对称性，在跨中截面布置电阻应变片来监测其在外荷载和预应力增量作用下的变形情况，沿着梁体纵向布置位移计来测量竖向挠度情况，测点布置及加载方案如图2。

图2 试验加载装置及测点布置

1.3 加载方案

采用液压伺服油压机配合计算机软件控制系统并利用1 000 kN千斤顶对试件进行分级加载。在加载过程中，通过计算机控制系统加以控制，初始加载频率控制在每5 min 1次，加载20 kN，随着荷载值的变大，钢梁接近屈服，之后减小加载频率，控制在每2 min 1次，加载10 kN，直到试件破坏为止。测点数据的记录采用DH3816静态测试系统加以采集记录，而荷载数据采集运用伺服液压计算机控制系统进行读数记录。

2 试验过程及结果

2.1 试验现象

加载点附近0.5 m范围内混凝土翼板裂缝的出现及发展情况如图3。

图3 加载点附近混凝土翼板裂缝发展

在加荷初期阶段，钢梁与混凝土表现出良好的组合作用，未见有任何异常。随着外荷载的增大，当加载到217.004 kN时，混凝土发出微小的响声，个别栓钉开始承受纵向剪力，出现内力从分布现象。加载至271.251 kN时，加载点附近的混凝土翼板底面出现横向裂缝，如图3(a)。随着继续加载，裂缝逐渐扩展延伸，伴随着更多的横向裂缝出现，并向混凝土侧板发展，此时中性轴向上移动，进一步导致翼板底部裂缝宽度变大，如图3(b)。当加载至613.026 kN时，加载点附近混凝土被压碎，钢梁达到极限状态，组合梁试件受弯破坏，停止加载，跨中挠度达到105.18 mm。特征荷载见表2。

表2 试验测试特征荷载

本次试验采用后张法对试件进行预应力加载，加载分为2步：第1步对预-1、预-2分别施加10 MPa预应力，第2步分别施加20 MPa预应力，得到的初始预应力值分别为54.764，70.744 kN。

预应力增量随荷载变化情况如图4。预应力组合梁承受荷载，由于梁的变形导致预应力筋产生变形，从而产生预应力增量，能进一步提高梁的承载能力。从图中可以看出，在开始阶段，预应力增量随着外荷载呈现线性关系增长，随着荷载的不断增大，当荷载达到401.45 kN时，由于梁体的变形加大，预应力筋的内力增量增长加快。试件破坏时，最大预应力增量达到119.12 kN。

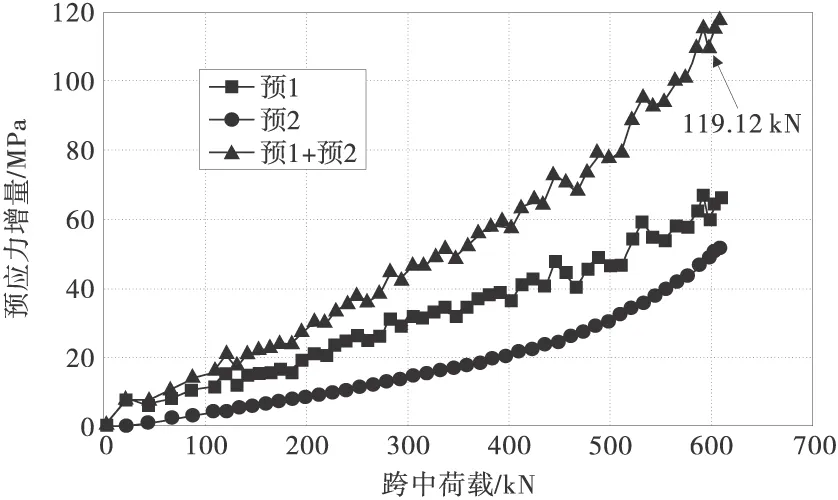
图4 预应力增量-荷载曲线

2.2 挠度特征

简支组合梁荷载-挠度关系曲线如图5。

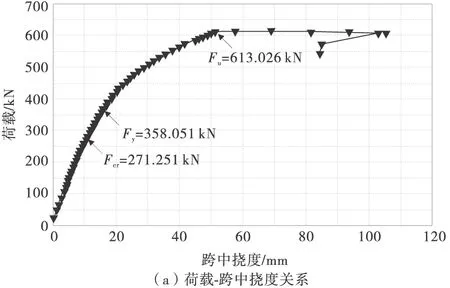
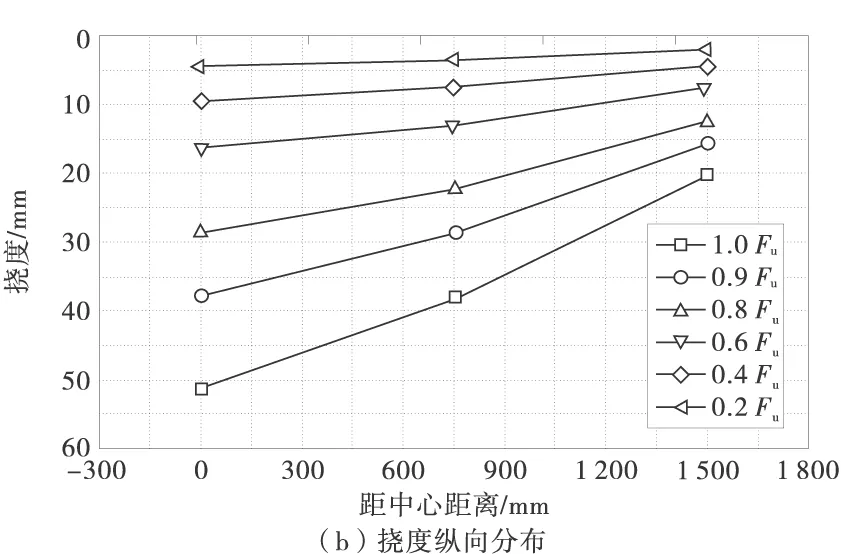
图5 荷载挠度关系曲线

图5(a)中描述了试验梁跨中挠度随荷载变化的关系，对比试验现象及试验结果，混凝土翼板的开裂并不会造成预应力组合梁挠度呈现较大幅度的非线性增长趋势，预应力组合梁特征曲线可分为3个阶段：第1阶段为弹性工作阶段，从开始加载到混凝土翼板出现裂缝(0﹤F≤271.251 kN)，此阶段内抗弯刚度基本保持不变；第2阶段为弹塑性工作阶段，从混凝土翼板开裂至组合梁达到极限荷载为终点，钢梁底板屈服后，钢梁的屈服范围逐渐向上延伸，钢梁应变呈现非线性增长，挠度变化较快；第3阶段为大变形段，当达到极限荷载后，混凝土翼板板顶压应变达到混凝土的极限压应变，混凝土板在跨中加载点附近处破坏，截面的抗弯能力迅速下降，混凝土翼板退出工作，结构出现大变形，此时最大挠度达到10.518 mm。

图5(b)中表述了0.2Fu,0.4Fu,0.6Fu,0.8Fu,0.9Fu,1.0Fu作用下挠度沿梁纵向分布关系。从图5(b)可看出：在加载初期，挠度沿组合梁纵向分布呈现良好的线性关系，当荷载达到0.4Fu时，挠度沿组合梁纵向分布开始向非线性转化，随着荷载的继续增加，其非线性程度表现得更加明显，直到试件破坏。

2.3 应变特征

不同荷载作用下混凝土翼板跨中截面应变沿板横向分布如图6。

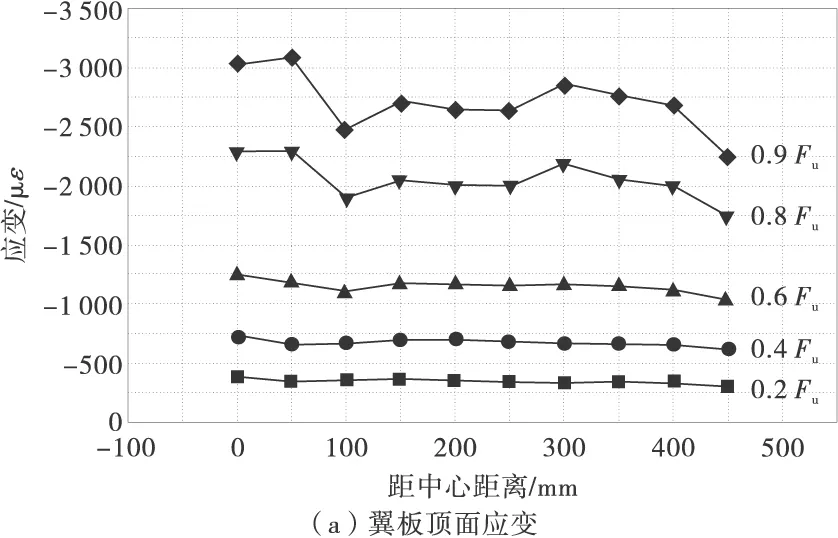
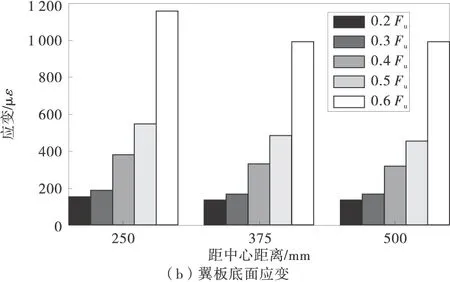
图6 跨中截面混凝土翼板应变分布

图6(a)为混凝土翼板顶面应变分布，可以看出：加载初期，应变沿横向分布比较均匀，越靠近板边缘，其应变有减小的趋势，但是这种现象不很明显。当加载到0.4Fu时，应变沿板横向分布不均匀程度更加明显，板中心与板边缘应变差值逐渐增大，随着荷载的继续增大，这种分布不均匀现象更加显著，当荷载达到0.9Fu时，应变达到最大，最大压应变达到-3 081 με，由于试验条件限制，当荷载达到1.0Fu时，应变片已坏，没有采集到数据。图6(b)为0.2Fu,0.3Fu,0.4Fu,0.5Fu,0.6Fu作用下，混凝土翼板底面跨中截面不同位置处应变分布。从图6(b)中发现，在越靠近混凝土翼板边缘的地方，其应变越小，且随着荷载的增大，这种应变分布不均匀趋势更加明显。由此推断，混凝土翼板发生了“剪滞效应”。

不同荷载作用下钢梁底板跨中截面应变沿板横向分布如图7。图7中显示了0.2Fu,0.4Fu,0.6Fu,0.8Fu,0.9Fu,1.0Fu作用下钢梁底板跨中截面处不同位置应变分布情况，从图7中可以看出，钢梁底板应变分布表现为中间小、两边大的特点，而且从试验加载开始到试件破坏，一直呈现出这种规律特征。由此推断，双箱钢梁底板同样出现了剪滞效应现象。当组合梁试件破坏时，钢梁底板最大拉应变达到4 209 με。

图7 钢梁底板应变分布

预应力组合梁结构在承受荷载时，由于混凝土和钢材的不同材料性质，导致二者之间变形出现不协调，为此需要研究其截面应变分布。图8给出了不同荷载作用下的截面应变分布。

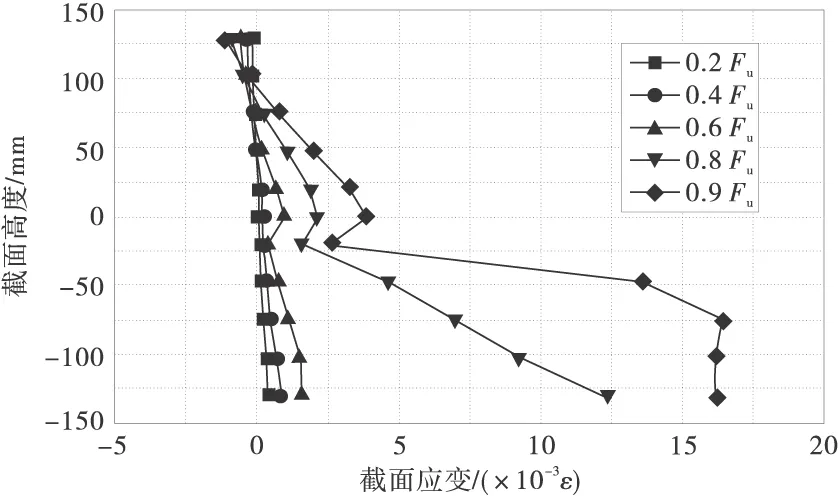
图8 截面应变分布

从图8中可以看出，在试验加载初期，组合梁结构中钢梁、混凝土翼板交界面处的应变差很小，符合变形平截面假定。随着荷载的增加，当混凝土翼板开裂，双箱钢梁进入弹塑性阶段，双箱钢梁底板出现翘曲现象，组合梁中和轴不断上升，交界面滑移增大，双箱钢梁应变急剧增长在破坏阶段已不满足平截面假定。

3 剪滞效应分析

3.1 基本假定

由双箱钢梁和混凝土翼板组合而成的宽翼缘双箱组合梁结构，其净跨为L0。Ec，Es，E0，Gc，Gs，G0，Ac，As，A0，Ic，Is，I0分别表示两种材料，及组合梁换算截面的弹性模量、剪切模量、横截面面积、抗弯惯性矩。在分析宽翼缘双箱钢-混凝土组合梁考虑剪滞效应和预应力增量作用下组合梁变形特征时，用到了如下基本假定：①不考虑相对滑移的影响；②两种材料满足线弹性假定，且二者挠屈位移相等；③翼板应变沿横向为二次抛物线分布；④在外荷载作用过程中，预应力筋始终保持为弹性体；⑤忽略预应力筋与转向块之间的摩擦损失，并且预应力筋内力处处相等；⑥预应力筋与组合梁的变形基本一致，忽略“二次效应”的影响。分析简化模型如图9。

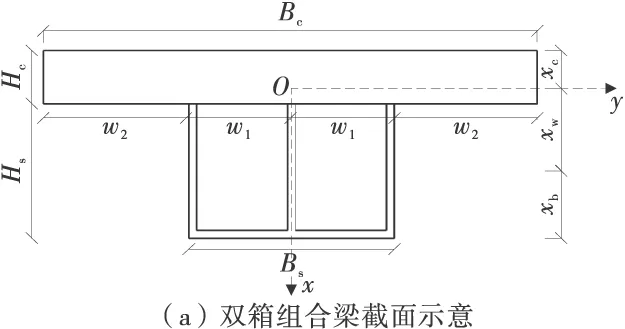
图9 双箱组合梁分析模型

3.2 剪滞效应计算

根据基本假定，双箱钢-混凝土组合梁任一点的纵向位移由纵向线位移ul(x,y,z)和由剪力滞引起的纵向翘曲位移uw(x,y,z)叠加而成，即：

u(x,y,z)=ul(x,y,z)+uw(x,y,z)

(1)

于是由式(1)可得双箱组合梁纵向翘曲位移函数表达式：

ui(x,y,z)=xiw′(z)+xiφi(y)fi(z)，(i=1,2,3,4)

(2)

式中：1，2，3，4分别为组合梁混凝土翼板w1段、w2段、钢梁腹板、钢梁底板位置相关参数；xi为各部分型心到组合梁形心轴的距离；w′(z)为梁的转角；φi(y)为双箱组合梁截面横向翘曲函数；fi(z)为翘曲函数沿纵轴向强度函数。其中：x1=-xc，x2=-xc，x3=xw，x4=xb；φ1(y)=φ4(y)=1-4[(y-0.5w1)/w1]2，φ2(y)=1-[(0.5Bc-y)/w2]3，φ3(y)=1；f1(z)=f2(z)，f3(z)=0。

将式(2)分别对z和y求偏导得：

(3)

则双箱组合梁应变能可表达为：

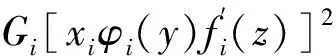
(4)

梁体受弯时荷载势能为：

Wp=∫vpM(z)w″(z)dVp

(5)

则双箱组合梁的总势能表达式为：

Π=U+Wp

(6)

根据最小势能原理，将式(4)、式(5)代入式(6)，并令其一阶变分为0，可求得双箱组合梁考虑剪滞效应后的控制微分方程为：

(7)

式中：

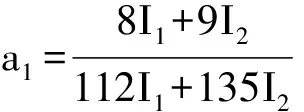
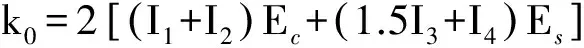
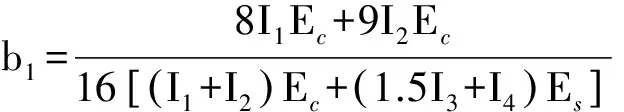
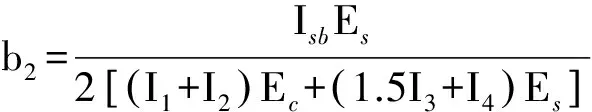
由式(7)解得：

(8)

f1(z)=

(9)

f4(z)=

(10)

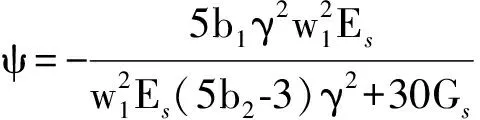
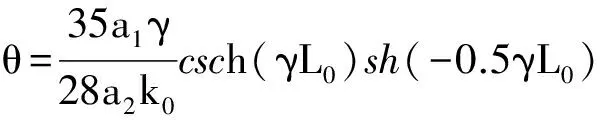
n=mθγch(0.5γL0)。

如图9，组合梁在外荷载及预应力作用下，任意截面剪力和弯矩可表示为：

(11)

M(z)=

(12)

根据能量守恒原理，外力所做的功等于结构的变形势能，即有基本方程：

W外=U1+U2+U3

(13)

式中：U1表示组合梁的弯曲应变能；U2表示预应力增量使梁体压缩产生的应变能；U3表示预应力增量引起的拉伸应变能。

外荷载对预应力组合梁所做的功W外为：

(14)

在外荷载作用下产生的弯曲变形能U1为：

(15)

预应力增量使梁体压缩产生的应变能U2为：

(16)

预应力增量引起的拉伸应变能U3为：

(17)

将式(14)～式(17)代入式(13)解得预应力筋内力增量：

(18)

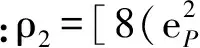
由式(8)～式(12)，式(18)得双箱组合梁挠度及对应应变函数表达式为：

(19)

(20)

3.3 算例及对比分析

以试验试件为例，该试件剪力连接程度为1.0，混凝土翼板应变极限荷载为Fcu=217.004kN。计算所用到的材料参数根据GB50017—2003《钢结构设计规范》和GB50010—2010《混凝土结构设计规范》来确定，Ec=37.56GPa，Es=206GPa，Ep=201GPa,Gc=14.4GPa，Gs=82.4GPa。几何参数取自试验试件：w1=0.13m，w2=0.37m， Hc=0.15m，Bc=1.0m，Hs=0.17m，Bs=0.26m，tw=0.01m，hw=0.16m，tb=0.01m,Dp=15.2mm。当F≤Fcu，剪力滞对比分析如下。

根据式(19)，可分别得到跨中荷载F=43.401，130.202，217.004kN时组合梁不同位置z=0.75，1.5，2.25m处挠度值，并与试验进行对比分析，如表3。根据推导式(20)，可分别得到跨中荷载F=43.401，130.202，217.004kN时混凝土翼板及双箱钢梁跨中截面不同位置应变值，对比分析如表4、表5。

表3 组合梁挠度理论与试验对比分析

表4 混凝土翼板跨中截面处应变对比分析

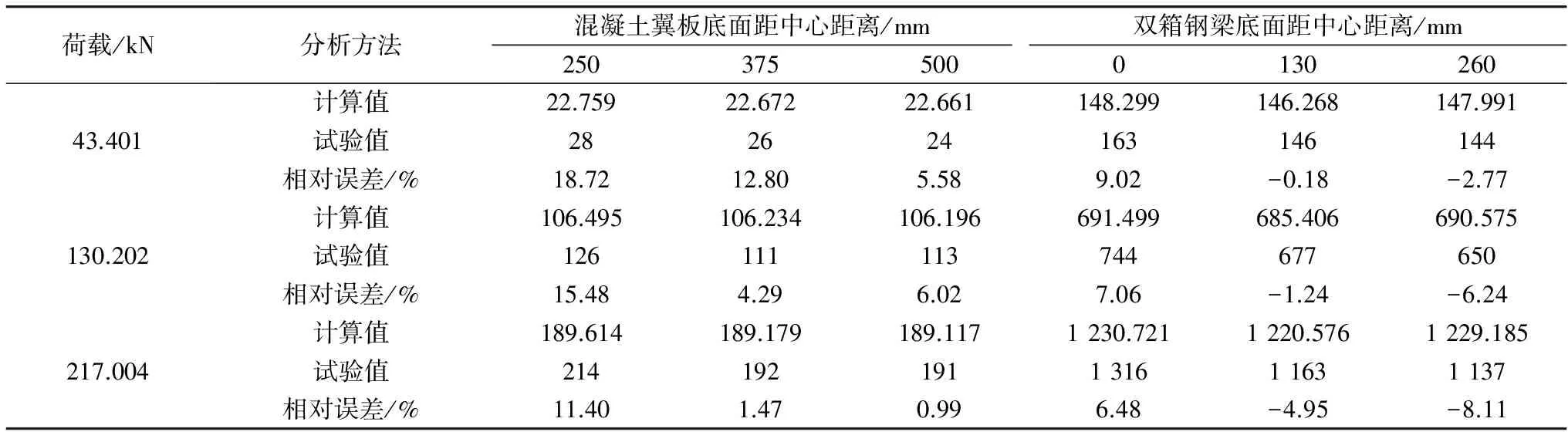
表5 混凝土、双箱钢梁跨中截面处应变对比分析

将表3～表5中相对误差汇总，如图10。分析可知，超过96.5%的数据落在15%以内，主要集中在4%左右，表明基于最小势能原理推导出的计算方法用于分析该类结构剪力滞问题具有很好的精度。

图10 相对误差分析

4 结 论

1)提出了一种新型的宽翼缘双箱型钢-混凝土组合梁结构，并对其在考虑体外预应力增量的作用下进行了试验研究，主要探讨了在跨中集中荷载作用下组合梁的应力、应变，以及挠度随荷载变化的情况。

2)通过找出混凝土翼板、双箱钢梁的位移形函数，基于最小势能原理，建立控制微分方程，求解出组合梁的形函数表达式。又根据能量守恒原理，解得预应力增量表达式，代入形函数表达式，最终求得考虑剪滞效应、预应力增量作用下的应变函数表达式，以及挠度函数表达式。

3)通过算例，在弹性范围内，对宽翼缘双箱钢-混凝土这种新型组合梁结构进行了剪滞效应对比分析，分析表明，其误差在15%以内，为分析组合梁结构关于剪滞效应问题、预应力增量问题提供了理论基础。

[1] 胡少伟.钢-混凝土组合结构 [M].郑州:黄河水利出版社,2005:5-20. Hu Shaowei.Steel-Concrete Composite Structure [M].Zhengzhou:Yellow River Conservancy Press,2005:5-20.

[2] 聂建国.钢-混凝土组合梁结构:试验、理论与应用 [M].北京:科学出版社,2005:2-16. Nie Jianguo.Steel-Concrete Composite Beam Structure:Theory and Application of the Test [M].Beijing:Science Press,2005:2-16.

[3] Fabrizio Gara,Graziano Leoni,Luigino Dezi.A beam finite element including shear lag effect for the time-dependent analysis of steel-concrete composite decks [J].Engineering Structures,2009,31 (8):1888-1902.

[4] 向中富,蒋俊秋,黄海东.连续箱梁剪力滞系数的固定端法求解[J]. 重庆交通大学学报:自然科学版,2014,33(5):1-6. Xiang Zhongfu,Jiang Junqiu,Huang Haidong.Fixed end method to solve shear lag coefficient of continuous box beam[J].Journal of Chongqing Jiaotong University:Natural Science,2014,33(5):1-6.

[5] 张元海,张清华,李乔.宽翼缘薄壁梁剪滞效应分析的变分解法 [J].工程力学,2006(1):52-56. Zhang Yuanhai,Zhang Qinghua,Li Qiao.A variational approach to the analysis of shear lag effect of thin-walled beams with wide flange [J].Engineering Mechanics,2006(1):52-56.

[6] Guo Jian,Sun Bingnan.Analysis of shear lag effect of steel-concrete composite box tower in cable-stayed bridge [J].Journal of Harbin Institute of Technology,2003,35(Sup1):269-271.

[7] Zhou Wangbao,Jiang Lizhong,Liu Zhijie,et al.Closed-form solution for shear lag effects of steel-concrete composite box beams considering shear deformation and slip [J].Journal of Central South University,2012,19 (10):2976-2982.

[8] 孙飞飞,李国强.考虑滑移、剪力滞后和剪切变形的钢-混凝土组合梁解析解[J].工程力学,2005(2):96-103. Sun Feifei,Li Guoqiang.A closed-form solution for steel-concrete composite beams with slip,shear lag and shear deformation [J].Engineering Mechanics,2005(2):96-103.

[9] 张元海,李乔.考虑剪滞变形时箱型梁广义力矩的数值分析 [J].工程力学,2010(4):30-36. Zhang Yuanhai,Li Qiao.Numerical analysis of generalized moment in box girder considering shear lag deformation [J].Engineering Mechanics,2010(4):30-36.

[10] 胡少伟,喻江,谢建锋.宽翼缘组合梁结构剪滞效应计算分析与试验研究 [J].应用数学和力学,2014,35(4):432-443. Hu Shaowei,Yu Jiang,Xie Jianfeng.Analytic solution and experimental study on shear lag effect of steel-concrete composite beams with wide flange [J].Applied Mathematics and Mechanics,2014,35(4):432-443.

Experimental Study and Analysis on Shear Lag Effect of PrestressedComposite Beam Structure

Hu Shaowei1, Yu Jiang1, 2, Xie Jianfeng1, Xu Aiqing3

(1. Nanjing Hydraulic Research Institute, Nanjing 210024, Jiangsu, China;2. College of Civil & Transportation Engineering, Hohai University, Nanjing 210098, Jiangsu, China;3. College of Mechanics & Materials, Hohai University, Nanjing 210098, Jiangsu, China)

In order to make an in-depth analysis on shear lag effect of prestressed steel-concrete composite beam structure, a new type of double-box steel-concrete composite beam with wide flange was proposed and researched through the test, and its load-stress curves, load-strain curves, and load-deflection curves were discussed under mid-span concentrated load. Based on the warping displacement model assumption, governing differential equations were established by the minimum potential energy principle, and expressions of strain and deflection were deduced considering both shear lag effect and prestressed increment. Finally, combining with the example, contrastive analyses on shear lag effect between test and theory were also launched within the elastic stage, analysis solution showed that the error within 15%.

bridge engineering; double-box composite beam; shear lag effect; prestressed increment; analytical solution

10.3969/j.issn.1674-0696.2015.04.02

2014-07-16；

2014-09-16

国家杰出青年基金项目(51325904)；国家自然科学基金项目(51279111)

胡少伟(1969—)，男，河南杞县人，教授，博士生导师，主要从事水工结构工程与材料方面的研究。E-mail: hushaowei@nhri.cn。

TU398;O302

A

1674-0696(2015)04-007-08