一个扩展的r矩阵及其应用
徐英,王素霞
(淮南师范学院金融学院,安徽淮南232038)
一个扩展的r矩阵及其应用
徐英,王素霞
(淮南师范学院金融学院,安徽淮南232038)
发展并应用孤立子方程的谱问题非线性化方法到对称矩阵Kaup-Newell方程上.得到了一个扩展的r矩阵,并应用r矩阵方法证明了对称矩阵kaup-Newell方程的有限维Hamilton系统是Liouville完全可积的.
对称矩阵Kaup-Newell方程;谱问题非线性化;r矩阵;可积Hamilton系统
1 引言
著名的r矩阵理论[1]经常被应用于研究约束孤子流,由孤子方程通过谱问题非线性化[2-12]可以得到这些约束孤子流的有限维可积Hamilton系统.所有这些约束孤子流都有Lax表示Lx=[U,V],其守恒积分可以由trLk,k∈Z表示,又由r矩阵关系
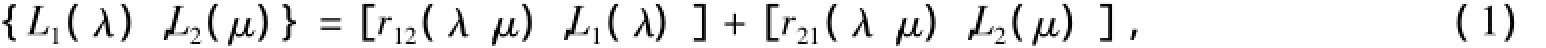
可以得到对合关系
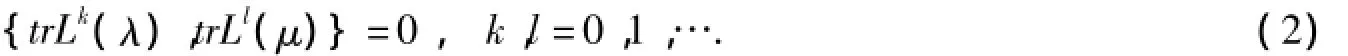
本文研究对称矩阵Kaup-Newell方程的谱问题双非线性化[5,12-15],得到了对称矩阵Kaup-Newell方程的一个有限维Hamilton系统,该有限维Hamilton系统具有Lax表示,让我们惊讶的是发现这个Lax算子所满足的形式不同于以往规范的r矩阵形式(1),而是满足如下扩展的r矩阵形式

其中A,B是任意的矩阵,从而应用r矩阵方法[1]可以得到上述有限维Hamilton系统是对合的,进而可以得到该有限维Hamilton系统是Liouville完全可积的.
2 对称矩阵Kaup-Newell方程
考虑4阶的Kaup-Newell谱问题
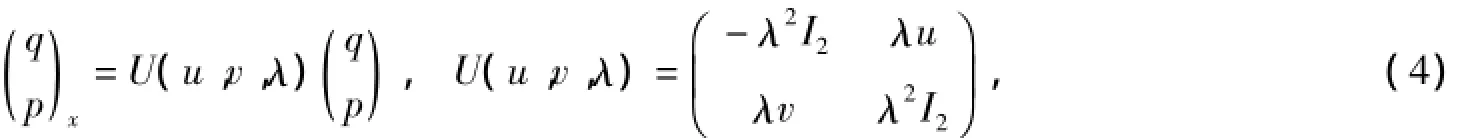
其中λ是谱参数,I2是2×2单位矩阵,u,v是2×2对称矩阵位势函数
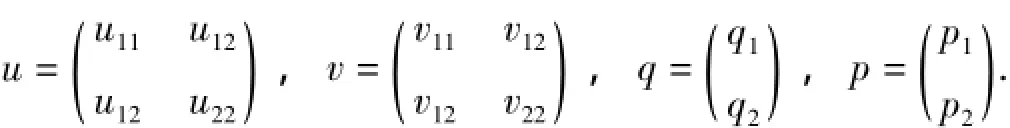
选取(4)的辅助谱问题
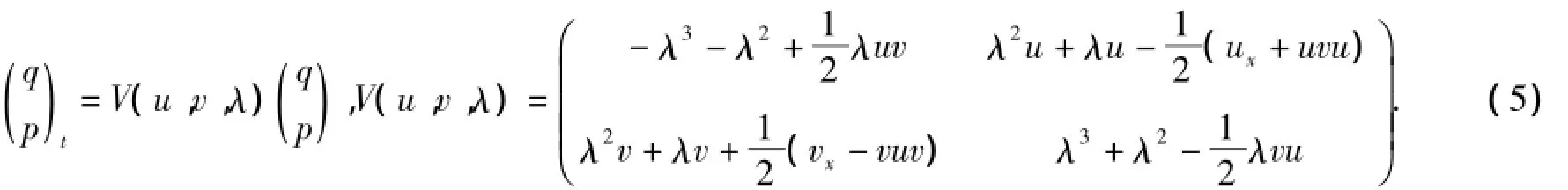
由(4)与(5)的相容条件即零曲率方程

给出矩阵Kaup-Newell方程

3 谱问题双非线性化与有限维Hamilton系统
首先给出一个引理[16].
引理1设Φ=(φ1,φ2,…,φr)T,Ψ=(φ1,φ2,…,φr)T满足谱问题及伴随谱问题Φx=U(u,λ)Φ,Ψx=-UT(u,λ)Ψ,其中U(u,λ)是与u,ux,…和参数λ有关的r阶方阵.设M=ΦΨT=(φkφl)r×r,则
选取N个互不相同的谱参数λ1,λ2,…,λN,考虑矩阵Kaup-Newell谱问题(4)和它的伴随谱问题
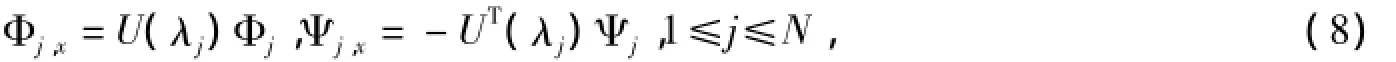
其中
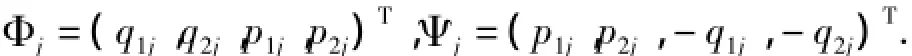
由引理1可得
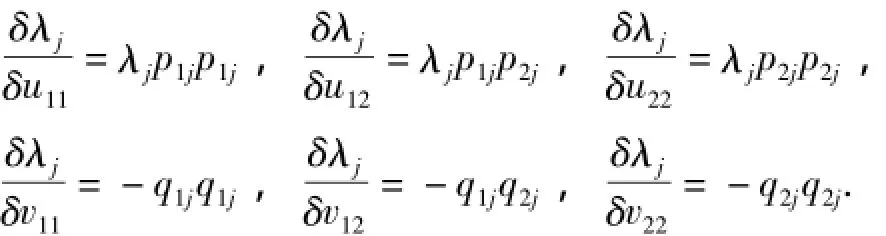
考虑Bargmann约束

其中
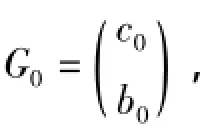
选取初值
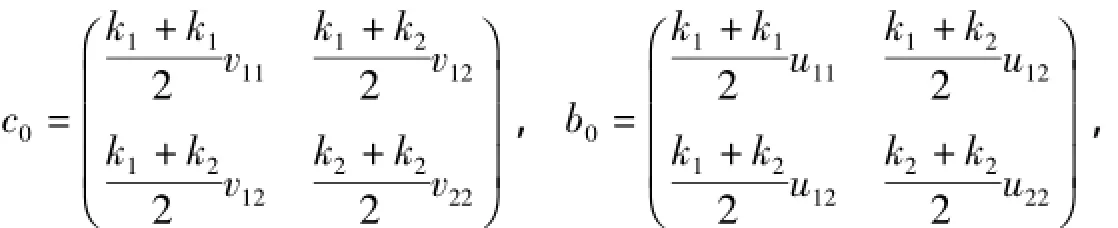
可得约束
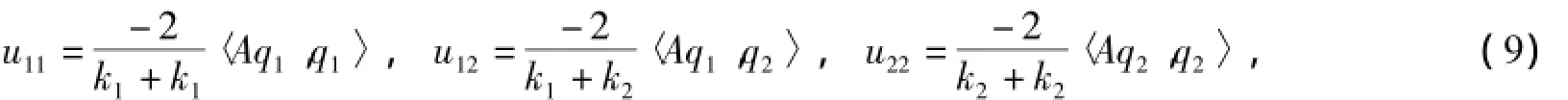

其中〈·,·〉表示RN中的标准内积,A=diag(λ1,λ2,…,λN),qs=(qs1,…,qsN),
Ps=(ps1,…,psN),s=1,2.
将(9)和(10)代入(8),得有限维系统

设q1j,q2j,p1j,p2j(1≤j≤N)是辛空间(R4N,ω2)的正则变量,相应的辛结构为

定义Poisson括号

定理1在辛结构(12)下,约束流(11)是Hamilton系统
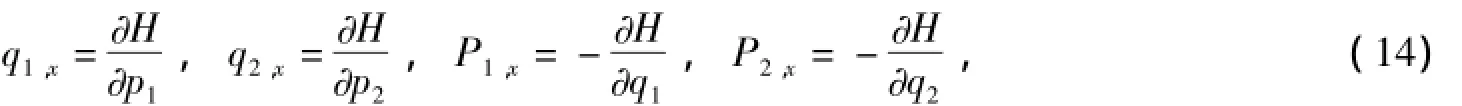
相应的Hamilton函数是
定理2有限维Hamilton系统(14)有如下Lax表示
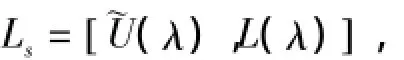
其中
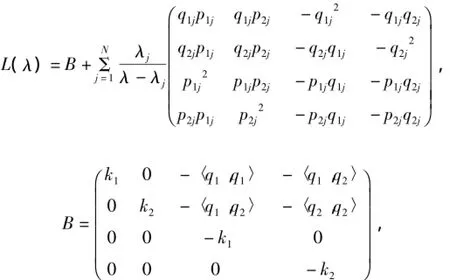
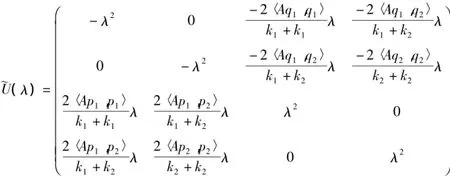
证明:记
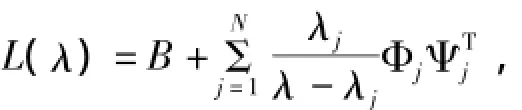
其中
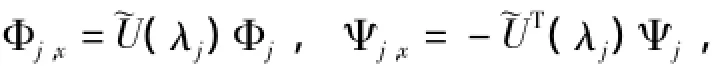
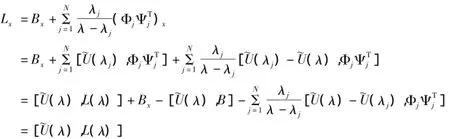
则
4 扩展的r矩阵与有限维Hamilton系统的可积性
引进记号:L1(λ)=L(λ)⊗I4,L2(μ)=I4⊗L(μ),其中定义C=A⊗B为C4(i-1)+k,4(j-1)+l=AijBkl,且A=(Aij),B=(Bkl).
在Poisson括号(13)下,通过直接计算可得到
定理3L(λ)满足如下r矩阵表示
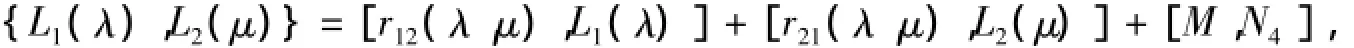
其中

其中ekl为第k行l列的元素为1,其它位置元素全为0的4×4矩阵.
这样,由r矩阵理论[1],可得
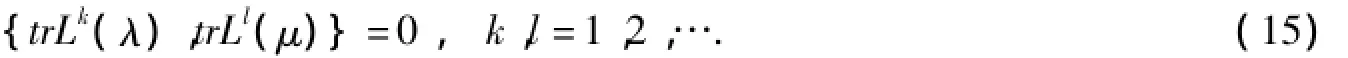
引理2如果矩阵L满足LT=-J-1LJ,则有(L2k+1)T=-J-1L2k+1J,k≥0,其中
由引理2可得trL2k+1(λ)=0,k≥0.
事实上,trL2k+1=tr(L2k+1)T=tr(-J-1L2k+1J)=-trL2k+1.
下面只需考虑trL2k.
定理4对于流变量x的Hamilton函数H与守恒积分是可交换的,即{H,trL2k}=0.
证明:因为trL2k(λ)(k=1,2,…)是守恒的,则有
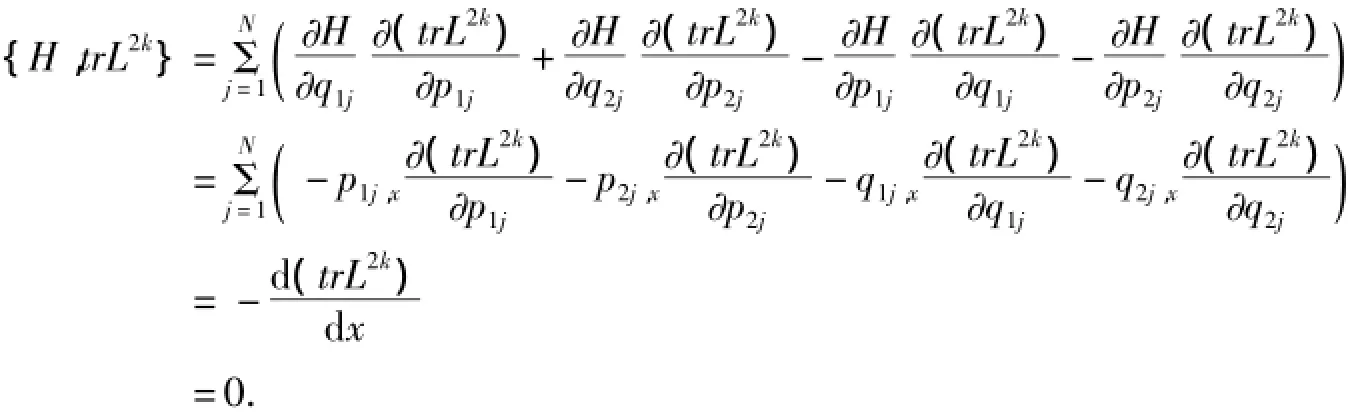
因此,trL2k(λ)(k=1,2)是守恒积分的母函数,而且可被表示成

其中E(k)j是守恒积分,由定理4,得{H,E(k)j}=0,并且由定理3,可得{E(k)i,E(j)l}=0,所以守恒积分的对合性得证.
下面考虑守恒积分的函数建立性.
定理5Hamilton系统(14)的守恒积分E(k)j(k=1,2,j=1,2,…,N)在R4N的稠密开子集上是函数独立的.
证明:由于E(k)j的解析性,只需考虑R4N上的一点P0.设P0是

其中ε是很小的实数.由(16)可以给出守恒积分的低阶质
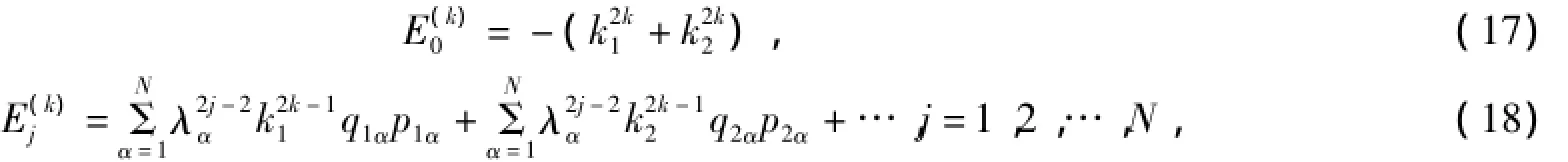
其中…表示其高阶项.
由方程(17),在点P0可得
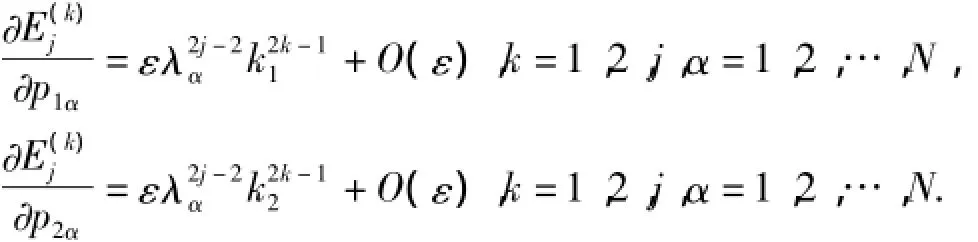
Jacobi行列式为
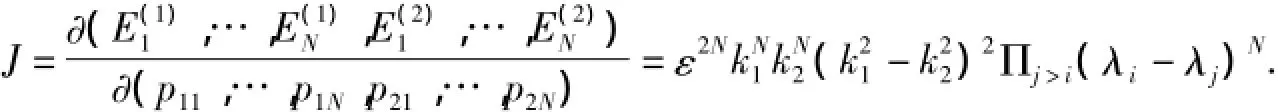
当ε足够小,并且ε≠0,J在P0点附近非零,因为所有的E(k)j都是实值函数,(E(1)1,…,E(1)N,E(2)1,…,E(2)N)关于实坐标的Jacobi矩阵是满秩的,
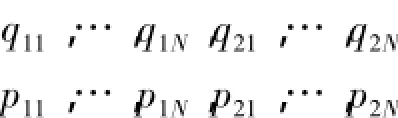
综上所述,可得如下结论
[1]Babelon O,Villet C M.Hamiltonian structures and Lax equations[J].Phys.Lett.B.,1990(237):411-416.
[2]Cao C W,Geng X G.Classical integrable systems generated through nonlinearization of eigenvalue problems[A].Proc Conf on Nonlinear Physics Research Reports in Physics[C].Berlin:Springer,1990.
[3]Cao C W.Nonlinearization of the Lax system for AKNS hierarchy[J].Science in China(A),1990(33):528.
[4]Qiao Z J.A new completely integrable Liouville's system produced by the Kaup-Newell eigenvalue problem[J].J.Math.Phys.,1993 (34):3110-3120.
[5]Ma W X,Strampp W.An explicit symmetry constraint for the Lax pairs and the adjoint Lax pairs of AKNS systems[J].Phys.Lett.A,1994(185):277-286.
[6]Ma W X,Zhou Z X.Binary symmetry constraints of N-wave interaction equations in 1+1 and 2+1 dimensions[J].J.Math.Phys.,2001(42):4345-4382.
[7]Ma W X,Zhou R G.Adjoint Symmetry Constraints of Multicomponent AKNS Equations[J].Chin.Ann.of Math.B,2002(23):373-384.
[8]Qin Z Y.A finite-dimensional integrable system related to a new coupled KdV hierarchy[J].Phys.Lett.A,2006(355):452-459.
[9]Zhou R G.Finite-dimensional integrable Hamiltonian systems related to the nonlinear Schr dingerequation[J].Stud.Appl.Math.,2009 (123):311-335.
[10]徐英,周汝光,王建文.WKIS方程的一个可积分解[J].徐州师范大学学报(自然科学版),2011,29(4):27-32.
[11]徐英,梁凤鸣.矩阵KdV约束流的r矩阵[J].泰山学院学报,2012,34(3):35-39.
[12]Xu Y,Zhou R G.Integrable decompositions of a symmetric matrix Kaup-Newell equation and a symmetric matrix derivative nonlinear Schr dinger equation[J].Applied Mathematics and Computation,2013,219(9):4551-4559.
[13]Ma W X.New finite-dimensional integrable systems by symmetry constraint of the KdV equations[J].J.Phys.Soc.Jpn.,1995(64): 1085.
[14]Ma W X.Symmetry constraint of MKdV equations by binary nonlinearization[J].Physica A,1995(219):467.
[15]Ma W X,Ding Q,Zhang W G.Binary non-linearization of Lax pairs of Kaup-Newell soliton hierarchy[J].Lu,IL Nuovo Cimento,1996(111):1135.
[16]Ma W X,Fuchssteiner B,Oevel W.A matrix spectral problem for AKNS hierarchy and its binary nonlinearization[J].Physica A,1996 (233):331-354.
An Extended r-Matrix Formula and its Applications
XU Ying,WANG Su-xia
(School of Finance,Huainan Normal University,Huainan,232038,China)
The approach of nonlinearization of spectral problem is extended and applied to the symmetric matrix Kaup-Newell equation.An extended r-matrix formula is presented.The complete integrability in the Liouville sense of the finite dimensional Hamiltonian system which results from the symmetric matrix Kaup-Newell equation is established in the framework of r-matrix.
the symmetric matrix Kaup-Newell equation;nonlinearization of spectral problem;r-matrix;integrable Hamiltonian system
O175.29
A
1672-2590(2015)06-0024-06
2015-09-25
淮南师范学院自然科学基金资助项目(2013XJ68)
徐英(1980-),女,山东沂南人,淮南师范学院金融学院教师.

