自适应随机共振形态学在液压泵振动信号特征提取中的应用

经 哲，郭 利

(军械工程学院导弹工程系，河北石家庄 050003)



自适应随机共振形态学在液压泵振动信号特征提取中的应用

经 哲，郭 利

(军械工程学院导弹工程系，河北石家庄 050003)

液压泵振动信号常湮没在强噪声背景中，为准确提取其特征频率，提出自适应随机共振形态学方法。首先采用以广义相关系数为目标函数的量子遗传算法对随机共振系统参数进行优化，再将优化后的参数代入随机共振系统对液压泵振动信号进行降噪预处理，最后利用形态学差值滤波器提取振动信号的特征频率。仿真实验和液压泵故障模拟实验结果表明，该方法能够准确地提取出振动信号的各种频率特征，优于其他特征提取方法。

自适应随机共振；形态学；特征频率；液压泵振动信号

0 引言

液压泵的振动信号采集方便，且包含了丰富的故障信息，是液压泵故障诊断的首选特征信号。这种特征信号通常具有非线性、非平稳性和冲击性等特点，小波变换、Hilbert-Huang变换等方法已被应用于这类信号的故障频率特征提取，但均存在一定的局限性[1]。数学形态学[2]与时域和频域的数学方法不同，该方法通过结构元素探针在信号中的移动来提取有用信号的冲击特征。虽然数学形态学方法可以抑制脉冲干扰[1]，但其滤除白噪声能力不足。随机共振是检测微弱信号的常用方法之一，与其他去噪方法不同，随机共振不仅只是单纯的消除噪声，而是充分利用噪声的部分能量，将其转化为信号的能量，从而达到去噪效果[3]。

为准确提取湮没在强噪声背景下液压泵振动信号的特征频率，提出一种基于自适应随机共振形态学的信号特征提取方法。该方法采用以量子遗传算法为优化算法的自适应随机共振对信号进行降噪预处理，然后利用形态学差值滤波器提取信号的频率特征。该方法克服了数学形态学滤除白噪声能力的不足的问题，与其他特征提取方法相比，能更准确地提取液压泵振动信号的各种频率特征。

1 数学形态学

1.1 数学形态学基本运算

数学形态学的基本运算包含腐蚀和膨胀两种算子[4]。设一维多值信号x(n)的定义域为X={0,1,2,…,N-1}，一维结构元素序列y(n)的定义域为Y={0,1,2,…,M-1}，其中N和M都是整数，且N>M，则x(n)关于y(n)的膨胀和腐蚀分别定义为：

(x⊕y)(n)=max[x(n-m)+y(n)]

(1)

(xΘy)(n)=max[x(n+m)-y(n)]

(2)

数学形态学中的腐蚀运算有抑制正向冲击和平滑负向冲击的作用，而膨胀运算则相反，在平滑正向冲击的同时抑制了负向冲击。

x(n)关于y(n)的开、闭运算分别定义为：

(x∘y)(n)=(xΘy⊕y)(n)

(3)

(x·y)(n)=(x⊕yΘy)(n)

(4)

数学形态学中的开运算常用来去除信号边缘的毛刺，同时可以滤除信号上方的峰值噪声；闭运算常用于平滑或抑制信号下方的波谷噪声，起到填补信号的漏洞和裂纹的作用。

1.2 形态学滤波器

利用形态学的开、闭运算可以构建2种常用的滤波器：平均滤波器(AVG)和差值滤波器(DIF)。二者分别表示如下：

AVG(x)=(x·y+x∘y)/2

(5)

DIF(x)=x·y+x∘y

(6)

AVG可以在消除信号正、负冲击的同时平滑信号，而DIF可以提取信号中的正、负冲击。

1.3 形态学结构元素

结构元素是形态学的基本算子，其形状和大小的选择对滤波效果有重要的影响。常用的形状有三角、半圆、菱形等。结构元素越复杂，计算量越大，提取信号的效果也越好。考虑到提取效果和计算量等综合因素，处理信号时常选用扁平的圆盘形作为结构元素[5]。

2 自适应随机共振形态学

2.1 自适应随机共振

随机共振系统由3个要素构成，分别为信号、噪声和用于信号处理的非线性系统，可用朗之万方程(Langevin Equation, LE)将这种双稳系统表示如下：

(7)

式中：V(x)=-ax2/2+bx4/4，为系统的势函数；a和b均为大于零的实数。

〈ζ(t),ζ(0)〉=2Dδ(t)

(8)

当驱动信号和噪声共同作用且与非线性系统达到某种匹配时，质点将从原来的势阱跃迁到另一个势阱，从而发生随机共振现象。

自适应随机共振通过调节输入噪声的强度或调节系统的参数[6]使系统达到随机共振状态。当系统自身的噪声强度较大时，再向系统中加入噪声时不但不会发生随机共振现象，而且会恶化系统的性能，而液压泵振动信号常常湮没在强噪声背景中，并不适合用调节输入噪声的方法使其达到随机共振的状态。调节系统参数的方法不需要信号和噪声的先验知识，只需调整系统的参数a和b，便可以使系统达到最佳共振状态，因此成为众多学者研究的重点。

本文利用量子遗传算法(Genetic Algorithm, GA)作为自适应随机共振优化系统结构参数的优化算法。量子遗传算法是基于量子计算原理的一种遗传算法，通过将量子的态矢量表达引入遗传编码，利用量子逻辑门实现染色体的演化，可在保持较好的种群多样性的同时，具有良好的全局搜索能力。

在自适应随机共振优化系统参数的过程中，目标函数的选取也至关重要。信噪比是最常用的目标函数之一，但信噪比并不适用于多频信号的检测[7]。针对上述不足，本文提出使用广义相关系数(General Correlation Function, GCF)作为QGA的目标函数。广义相关系数建立在互信息和互相关系数的基础上，是判定变量间广义相关程度的一种指标，其表达式如下：

(9)

式中：MS(X,Y)代表随机变量X与Y的互信息熵；S(X)、S(Y)分别表示X、Y的信息熵。

2.2 基于自适应随机共振的形态学

利用随机共振对信号进行预处理。选用量子遗传算法对随机共振的系统参数进行优化，以广义相关系数作为优化算法的目标函数，使系统在当前噪声强度下达到最佳共振状态。再将优化后的参数代入随机共振系统，利用步长为h=1/fs的四阶龙格-库塔方程对随机共振系统进行求解，得到系统的输出信号。传统随机共振因遵守绝热近似理论，只能检测频率远小于1 Hz的信号，在实际工程应用中，频率常常远大于1 Hz，故采用变尺度随机共振方法[8]先对采集到的信号进行线性压缩，再按压缩尺度还原实测数据。最后利用形态学差值滤波器来提取输出信号的特征频率，形态学的结构元素选择圆盘形。自适应随机共振形态学流程图如图1所示

图1 自适应随机共振形态学流程图

3 仿真信号

设仿真信号为

x(t)=x1(t)+x2(t)+x3(t)

式中：x1(t)=1.2×cos(2×π×30×t)+1.6×cos(2×π×50×t)，是频率为30 Hz和50 Hz的谐波信号；x2(t)是噪声强度为1的高斯白噪声；x3(t)=exp(-20t)·sin(20×π×t)，是周期性指数衰减冲击信号。

采样频率为fs=1 kHz，采样时间为1 s。经量子遗传算法优化，自适应随机共振的系统参数选取如下：a=2.666 2，b=0.345 76。本文设置压缩倍数为250倍。

此实验的目的在于提取出谐波信号频率的同时提取信号中频率为20 Hz的冲击信号频率成分。原始信号和经随机共振处理的信号频谱图如图2、图3所示。

图2 原始信号的频谱图

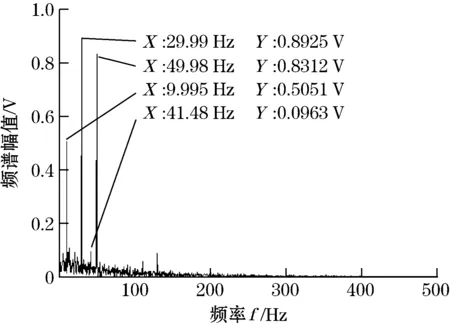
图3 经自适应随机共振处理后的信号频谱图

显然，原始信号和经随机共振处理后的信号频域图中检测到的29.99 Hz和49.98 Hz与谐波信号中30 Hz和50 Hz非常相近。但原始信号的频谱图并不能提取20 Hz的冲击成分，而经自适应随机共振处理后的信号频谱图中，20 Hz的1/2倍频突出，2倍频较明显，但20 Hz本身已经湮没在其他频率中。利用形态学差值滤波器提取经自适应随机共振预处理后的信号特征频率，得到的频谱图如图4所示

图4 经自适应随机共振形态学处理后的信号频谱图

由图4可知，经自适应随机共振形态学处理后的信号频谱图不但可以提取出信号的谐波频率，19.99 Hz与39.98 Hz与冲击信号的基频20 Hz和2倍频40 Hz非常相近，且如表1所示，信号1倍频与2倍频的振幅较文献[9]中的EEMD形态学和LMD形态学略高，所以自适应随机共振形态学提取故障特征频率的效果较好。

表1 频率的振幅对比

4 工程实测信号

在液压泵的常见故障模式中，滑靴松动和斜盘磨损是目前最容易发生的故障。若液压泵在工作过程中出现了滑靴松动的情况，轻则发生振动，降低液压泵的寿命；严重的会导致滑靴脱节或者使塞颈部断裂，发生重大事故。同时，斜盘式轴向柱塞泵包含的多对摩擦副中，滑靴与斜盘之间的摩擦副最为复杂[10],对液压泵的性能影响较大。

本文采用试验器件名称及型号如表2所示：其中，驱动电机的额定转速为1 480 rP/min；液压泵的柱塞数为7，理论排量为10 mL/r，额定转速为1 500 rP/min，液压泵主溢流阀压力为10 MPa，采样频率为20 kHz，采样点数为10 000。由于泵轴的转速为1 500 rP/min,单个柱塞附加冲击的基频为f=n/60(n为电机的转速)，则本试验的液压泵的冲击振动基频为1 480/60×7=172.667 Hz。液压泵故障模式试验台、传感器安装位置以及松靴、斜盘磨损的故障部件分别如图5、图6和图7所示。

表2 试验器件名称及型号

图5 液压泵故障模式试验台图

图6 传感器安装位置

(a)松靴故障件

(b) 斜盘磨损故障件

采集到的松靴和斜盘磨损的信号的时频图分别如图8所示。

通过对图8中各图进行比较分析可知，采集松靴状态下的信号的频谱能量较分散，主要集中在260 Hz、516 Hz和738 Hz等频率上，而斜盘磨损状态下的信号的频谱能量较集中，主要集中在516 Hz处。采集到的信号均不能提取信号的基频172.667 Hz。利用随机共振和自适应随机共振形态学分别对故障信号进行处理，得到的对比图分别如图9、图10所示。

通过对图9进行比较分析可知，对松靴信号频谱而言，自适应随机共振与自适应随机共振形态学提取出的频率172 Hz、344 Hz、516 Hz与信号的基频172.667 Hz、2倍频345.334 Hz、3倍频518.001 Hz较为相近，但经自适应随机共振处理后的松靴信号中，50 Hz等频率对信号的故障特征提取存在一定的干扰，而自适应随机共振形态学提取的频率特征较为明显，且提取出的690 Hz和862 Hz与4倍频690.668 Hz、5倍频863.335 Hz也十分相近。

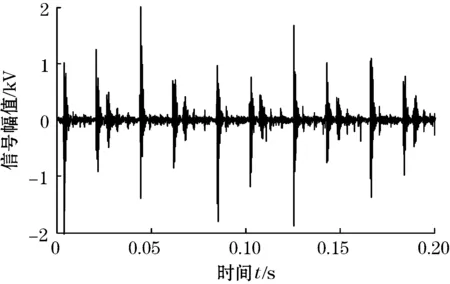
(a)松靴状态下的时域图

(b)松靴状态下的频谱图

(c)斜盘磨损状态下的时域图

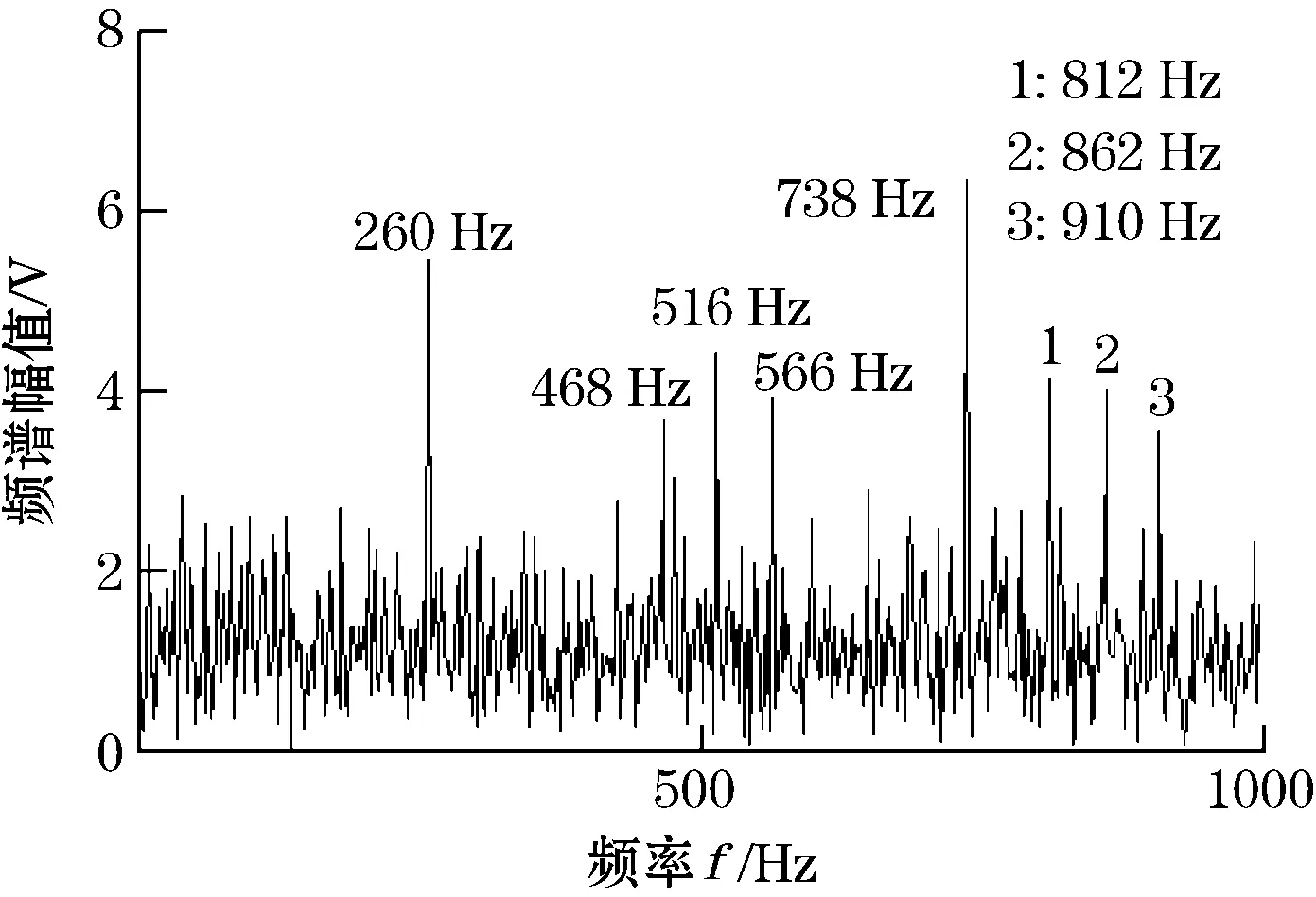
(d)斜盘磨损状态下的频谱图图8 不同故障状态下信号的时频图

(a)自适应随机共振处理后的信号包络谱图

(b)自适应随机共振形态学处理后的信号包络谱图图9 松靴状态下信号的包络谱图

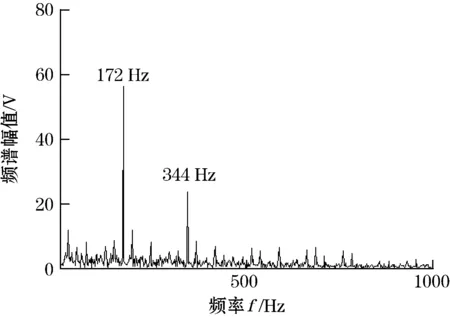
(a)自适应随机共振处理后的信号包络谱图

(b)自适应随机共振形态学处理后的信号包络谱图图10 斜盘磨损状态下信号的包络谱图

而对于斜盘磨损信号而言，经自适应随机共振处理后的信号频谱中只有172 Hz与344 Hz清晰可见，但自适应随机共振形态学处理后的信号频谱图中，516 Hz、688 Hz和860 Hz是信号基频的3、4、5倍频的体现，可见自适应随机共振形态学可以更好的显示信号的频谱特征。

5 结论

针对液压泵振动信号常湮没在强噪声背景中问题，提出自适应随机共振形态学的特征提取方法，在进行降噪预处理的同时能够准确地提取信号的频率特征。仿真实验结果表明，自适应随机共振形态学在提取信号特征频率方面优于其他特征提取方法；液压泵模拟故障实验表明，该方法能够应用于工程实际，为液压泵故障预测和诊断打下良好基础。

[1] 侯高雁,吕勇,肖涵,等. 基于EEMD自适应形态学在齿轮故障诊断中的应用. 振动与冲击, 2014,33(18):145-148.

[2] SERRA J. Morphological filtering: an overview. Signal Process. 1994,38(4):3-11.

[3] 李忠虎,蔡志全. 基于调制随机共振的微弱信号频率检测方法. 仪表技术与传感器, 2014(8):104-106.

[4] 罗洁思,于德介,彭富强,等. 基于EMD的多尺度形态学解调方法及其在机械故障诊断中的应用.振动与冲击, 2009,28(11):84-86.

[5] 赵昭,刘利林,张承学,等. 形态学滤波器结构元素选取原则研究与分析. 电力系统保护与控制, 2009,37(14):21-25.

[6] 李相臣.自适应随机共振信号检测系统的设计与实现. 仪表技术与传感器, 2013(12)：105-108.

[7] 王曦. 基于随机共振的弱信号检测研究：[学位论文]. 北京：北京邮电大学, 2010.

[8] 范胜波，王太勇，冷永刚，等.基于变尺度随机共振的弱周期性冲击信号的检测.中国机械工程, 2006,17(4)：387-390.

[9] 侯高雁,吕勇,李友荣,等. LMD形态学与EEMD形态学在故障诊断中的对比研究. 仪表技术与传感器, 2014(8)：107-110.

[10] 张长英，龚晓群，李萍萍，等.斜盘式轴向柱塞泵的减摩降噪措施.液压与气动, 2013(12):118-120.

欢迎订阅 邮发代号：8-69

月刊 10元/期

《仪表技术与传感器》杂志

主要刊载内容：

传感器技术 仪器仪表

系统与应用 研究与开发

订阅：沈阳市大东区北海街242号(110043)tel：024-88718630

网址：www.17sensor.com E-mail:info@17sensor.com

Application of Adaptive Stochastic Resonance Morphologyin Hydraulic Pump Vibration Signal Feature Extraction

JING Zhe, GUO Li

(Department of Missile Engineering, Ordnance Engineering College, Shijiazhuang 050003, China)

In order to extract the frequency characteristic of hydraulic pump vibration signal which is in high noise background, adaptive stochastic resonance(ASR) was proposed. Firstly, quantum genetic algorithm(QGA) was used to optimize the stochastic resonance system’s parameters, meanwhile the genetic correlation function(GCF) was used as the object function of QGA. Then，make the optimization parameters into the stochastic resonance system for hydraulic pump vibration signal pretreatment. At last, the morphologic filter was used to extract the characteristic frequencies from vibration signal. Through numerical simulations and hydraulic pump fault simulation tests, the proposed method can be used to clearly extract various characteristic frequencies of vibration signals and it is superior to the others.

adaptive stochastic resonance; morphology; characteristic frequency; hydraulic pump vibration signal

国家自然科学基金项目(51275524)

2015-05-15

TN911;TH16

A

1002-1841(2015)08-0092-04

经哲(1989—)，硕士研究生，主要从事装备状态监测和故障预测方面研究。E-mail：jingzhe_happy@163.com