自锚式悬索桥主缆架设监控

包大海， 袁堂超， 陆久飞

(长安大学公路学院， 西安710064)



自锚式悬索桥主缆架设监控

包大海， 袁堂超， 陆久飞

(长安大学公路学院， 西安710064)

自锚式悬索桥在缆索体系施工过程中，主缆线形控制贯穿整个施工过程。主缆架设作为主缆线形控制的首要环节直接影响着主缆线形能否达到设计要求。以浙江中湖大桥主缆架设为例，论述了主缆空缆线形各控制点的确定方法及处理措施；对比标准状态下解析法与有限元法计算主缆空缆线形结果；研究了无应力索长、跨度、温度对索股垂度的影响，以便快速、精准地确定基准索股线形。

桥梁工程；自锚式悬索桥；施工控制；主缆架设

引言

自锚式悬索桥是一个自平衡体系，主缆作为主要的传力部件，主缆线形直接影响着全桥整体受力[1]。主缆线形控制作为自锚式悬索桥施工控制重要组成部分，贯穿整个施工过程。主缆锚固点、散索套IP点和主索鞍IP点作为主缆线形主要控制点，在主缆架设前必须确定其初始状态。主缆架设作为主缆线形控制第一个环节，其空缆线形直接影响着全桥最终受力能否达到设计要求。对于由预制平行钢丝索股(PPWS)[2]组成的主缆而言，其空缆线形主要由基准索股线形控制。基准索股线形主要受索股无应力长度、跨度和温度影响。研究基准索股线形与各影响因素之间关系，对基准索股线形快速调整具有重要的指导意义。

1 工程概况

中湖大桥[3]是一座主跨120 m的三跨混凝土自锚式悬索桥，跨径组合为45 m+120 m+45 m，桥梁全长214 m，横断面宽30 m。主梁为现浇混凝土格子梁体系，主塔为门式钢筋混凝土框架，全桥共两根主缆，采用预制平行钢丝索股(PPWS)，每根主缆由37束平行钢丝组成，每一束由91根φ5.0 mm的镀锌高强丝组成，吊杆纵向间距5 m，横向间距17 m，全桥吊杆共74根，采用GJ15-22环氧涂层钢绞线成品索，共869.78 m。大桥整体布置如图1所示。

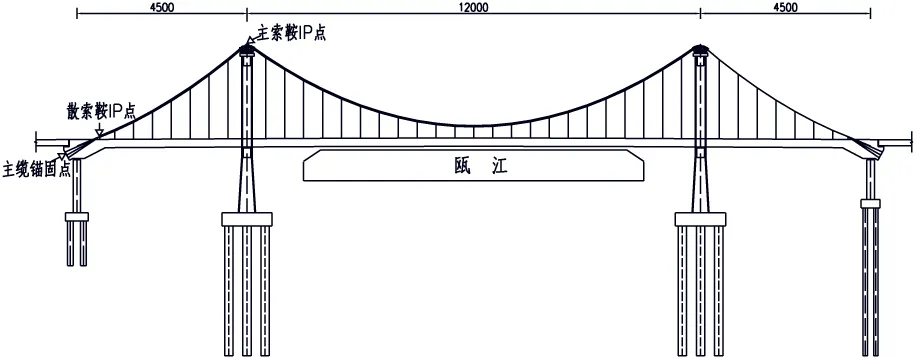
图1 全桥整体布置图2空缆线形各控制点的确定及部分处理措施

自锚式悬索桥索股架设是在主塔、主梁施工完成，猫道架设完毕后进行的[4]。主缆锚固点、散索套IP点和主索鞍IP点作为空缆线形的主要控制点，在索股架设前必须确定。由于施工过程中不可避免地会存在误差，设计中的一些材料特性并不能真实地反应现场实际，伴随着施工的进行必须对结构状态进行调整，确保达到设计状态。

主索鞍IP点：主索鞍设置在主塔上，主塔塔顶偏位及标高直接影响着主索鞍IP点的确定。主塔修筑完成其偏量主要受温度影响，在索股架设前必须对桥塔进行周日位移持续性观测。

主梁锚固点、散索套IP点：这两个控制点设置在主梁上，由多次稳定温度情况下的测量结果确定。主梁容重、弹性模量在主梁浇筑完成后，根据实际情况进行修正。

主缆参数：主缆各索股在加工完成后，会对部分索股进行张拉试验，根据实验结果修正主缆弹性模量等各方面材料参数。

经过现场多次测量及采用数值分析法(悬链线理论)[5-7]和有限元分析法计算，得到中湖大桥在稳定温度、自由状态下各控制点的偏位及标高见表1。

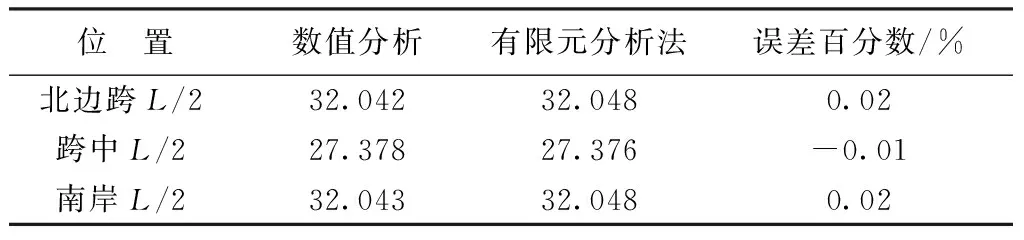
表1 不同计算方法求得空缆各控制点标高(单位：m)

在结构控制点确定以后，必须根据现有实际情况对全桥整体进行受力分析。对个别由于控制点差异较大而引起结构局部受力较大、施工不便的进行适当调整，确保全桥结构在施工中安全、简便地达到目标状态。

本桥主塔下部结构属于高桩承台，主缆架设初期主塔塔顶偏位受不平衡水平力影响较大。而主索鞍设置预偏的主要目的是为了减少空缆状态下边、中跨主缆不平衡水平力对主塔塔顶偏位的影响。预偏量设置最理想状态是塔顶没有不平衡水平力出现。由图2可以看出本工程裸塔具有一定初始偏位，且上下游偏位不一致。为了便于后期结构分析和吊杆对称张拉，需在设置主索鞍预偏时考虑主塔偏位不同步影响，保证主索鞍IP点上下游绝对里程一致。主塔标高较设计值偏高，可以通过在保证中跨失跨比不变的情况下，适当调整主缆线形。

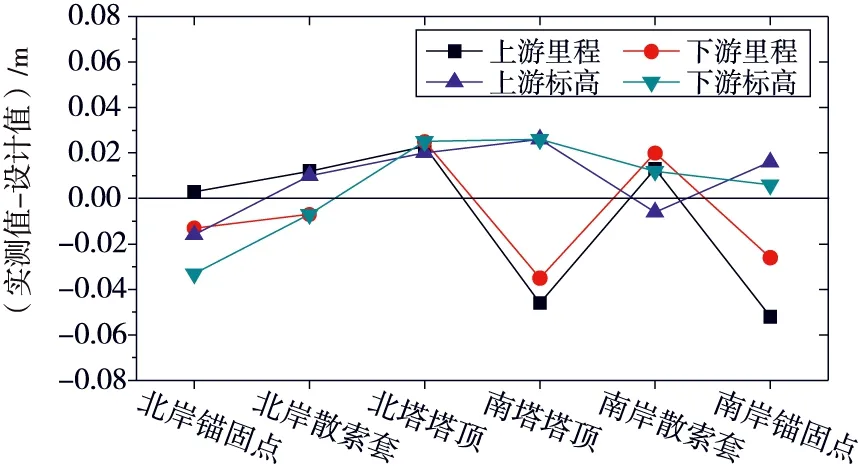
图2 中湖大桥各控制点偏位

由于工程进度需要主缆在主梁修筑期间开始生产，主缆各索股无应力长度已经确定。由图2可以看出，主缆锚固点实测值与设计值最大差5.2 cm。虽然主缆在生产时锚头处有±6 cm的调节量，但是为了减少因主缆锚具锚头脱空需重新调整索股线形的现象，本工程在南岸上游后锚段增设了3 cm与螺母材质相同的垫块。

3 空缆线形计算

空缆线形计算是本桥施工控制的关键环节。通过大型商业软件Midas/Civil建立中湖大桥成桥模型。全桥共建立626个单元、623个节点，其中混凝土格子梁采用鱼骨式梁单元模拟。主缆与吊杆采用索单元考虑，吊杆下锚点与主梁之间采用刚性连接，由于桥下部结构属于高桩承台主塔，必须考虑受不平衡水平力影响较大的桩基偏位。结构空缆状态模型如图3所示。根据悬索桥成桥状态与空缆状态主缆无应力长度不变的原则[8]，通过倒拆分模型[9-10]求出本工程在主缆建设前的初始状态、主索鞍和散索套的预偏量。并与现场初始状态实测值进行对比。对差异较大的控制点通过适当修正主缆无应力长度、主索鞍和散索鞍预偏量，通过正装模型[9-10]按照实际施工顺序达到合理成桥状态。

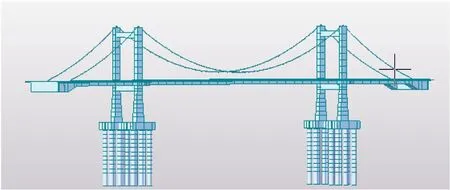
图3 大桥空缆模型

主缆在空缆状态下只受自重作用，其空缆线形为悬链线。由表1可以看出，采用Midas/Civil有限元软件计算主缆空缆线形与数值分析法计算结果较为接近，对于中小跨径自锚式悬索桥而言，数值分析法的计算精度满足工程要求。

4 索股架设

在主索鞍、散索套预偏量设置完毕后，主缆的空缆线形也随之确定。由于索股线形受温度荷载影响较大，基准索股线形精确调整必须在环境温度稳定的条件下进行。如何快速、精准的使基准索股空缆线形达到设计要求是自锚式悬索桥施工过程中制约工程进度和质量的重要环节。

理论上讲，主缆索股在生产过程中会对各跨控制点进行精确标记。但是由于主缆弹性模量、主梁自重、索股架设温度、各控制点间距及高差都与理论值存在差异，主缆索股架设期间各标记点无法用于精确控制主缆线形。由于索股仅在自重作用下是一条悬链线，而悬链线的线形主要用垂度表征(垂度指悬链线两端点连线中心到悬链线中心的距离)。因此研究索股无应力索长、跨度和温度对垂度的影响，对后期基准索股线形调整及观测具有重要指导意义。

4.1 索股无应力索长与垂度之间的关系

在跨度与索股温度不变的情况下，通过调整各跨索股无应力长度计算出各跨相应垂度。根据模型计算结果以及调索的实测数据发现，主缆垂度和索长之间的关系可近似拟合为线性关系，如图4所示。

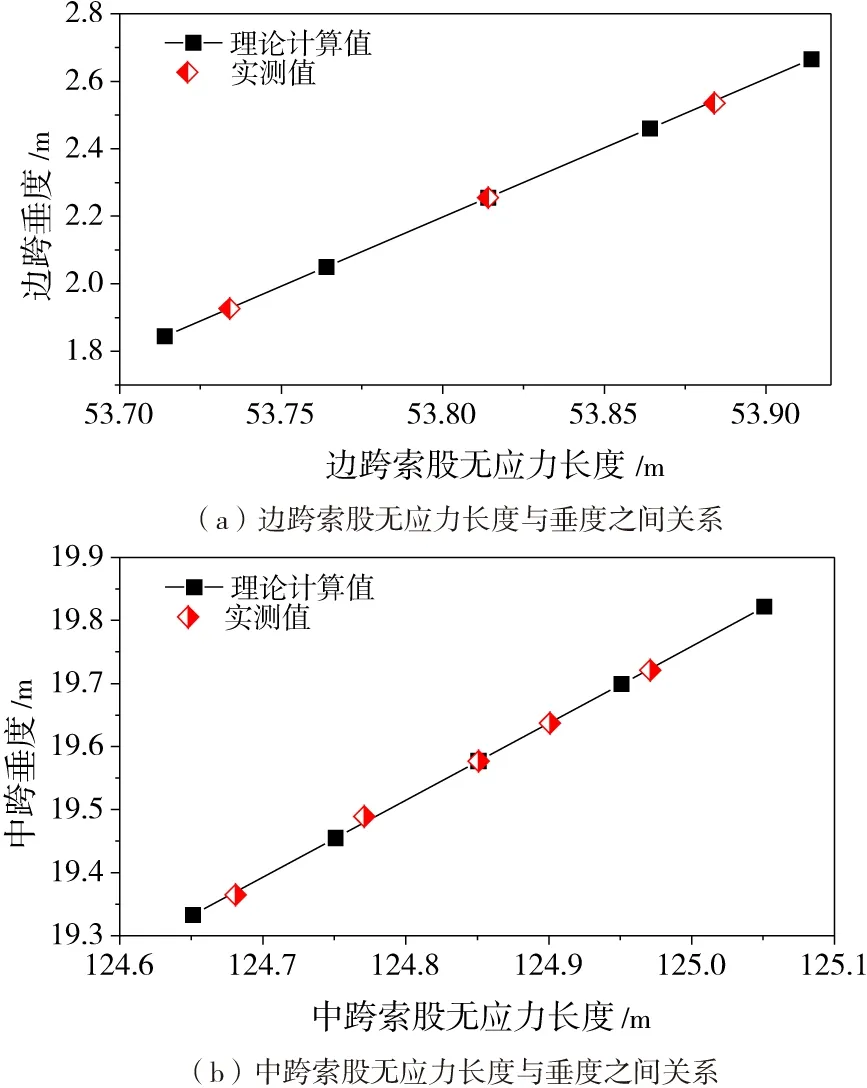
图4 边跨、中跨索长与垂度之间的关系

由图4可以看出在索股线形实际调整过程中，索股索长与垂度之间的线形关系与模型计算结果是相符的。将计算结果与现场实测数据进行拟合可以得到：

边跨：Δf边=4.10ΔL边

中跨：Δf中=1.2225ΔL中

其中，Δf边、Δf中为边、中跨垂度改变量，ΔL边、ΔL中为边、中跨无应力索长改变量。

4.2 索股跨度与垂度之间的关系

在索股长度与温度不变的情况下，通过调整索股跨度计算出各跨相应垂度。根据模型计算结果以及实测数据发现，主缆垂度和索长之间的关系可近似拟合为线性关系，如图5所示。

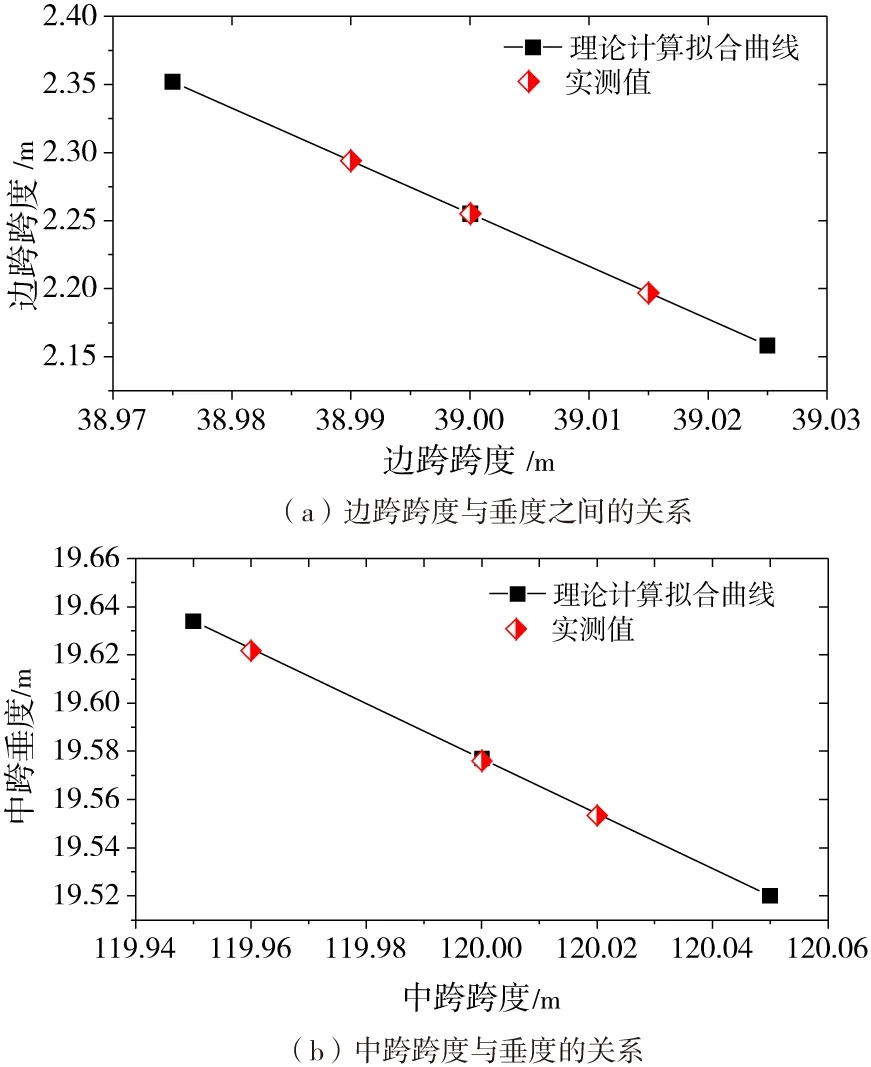
图5 边跨、中跨跨度与垂度之间的关系

由图5可以看出索股跨度与垂度之间符合线形关系，通过模型计算与实测结果相结合拟合出索股跨度与垂度之间的关系：

Δf边=-3.88ΔL边

Δf中=-1.14ΔL中

其中，ΔL边、ΔL中为边、中跨跨径改变量。

4.3 索股温度与垂度之间的关系

主缆在下料时的无应力长度是以20 ℃为基准，但在索股实际架设期间环境温度是随着季节与时刻而改变的。为了确保主缆索股线形能够达到设计状态，在索股线形调整期间温度修正是非常重要的。在跨度不变的情况下，温度变化其实可以简化为索股索长的改变。因而可以直接推导出温度与垂度之间的关系。

Δf边=4.10ΔL边= 4.10×53.8144×1.2×10-5×Δt= 2.648×10-3×Δt

Δf中=1.2225ΔL中= 1.2225×124.8509×1.2×10-5×Δt= 1.832×10-3×Δt

基准索股线形调整需要在稳定温度((长度方向Δt≤2 ℃，横截面Δt≤1 ℃)下进行，一般设在夜间(22∶00～02∶00)。由于天气、施工等因素影响，现场调索可用时间较短。基准索股线形调整时，首先要根据现场测量结果通过索股跨径、温度与垂度之间的关系确定各跨基准索股线形；在索股线形调整过程中根据索长与垂度之间的关系，可以很快使索股线形达到设计要求；在基准索股线形持续性观测(2～3天)过程中，由于受温度作用主塔偏位、主缆温度都会改变，根据换算后的结果判断索股线形是否稳定。基准索股垂度调整时允许误差：索股中跨跨中±L/20 000(L为跨径)=6mm，边跨跨中为中跨跨中的2倍，上下游基准索股高差为10mm。一般索股参考基准索股±5mm。

5 结束语

本文以中湖大桥为例，详细介绍了混凝土自锚式悬索桥在索股架设初期主缆线形各控制点的确定方法以及个别影响较大控制点的处理方法；对比有限元法与解析法(悬链线理论)计算空缆线形结果，对于中、小跨径自锚式悬索桥解析法计算结果能够满足工程精度的要求；在基准索股架设前能够将索股无应力长度、跨度和温度与垂度之间关系确定，对后期基准索线形快速调整及持续性观测具有重要意义。

[1] 龙飞,许福友,张哲.自锚式悬索桥的特点及工程应用[J].中外公路,2010(5):131-136.

[2] 罗喜恒,肖汝诚,项海帆.悬索桥主缆架设过程分析[J].中外公路,2004(2):8-11.

[3] 韩旭辉,袁阳光,陈安洋,等.自锚式悬索桥主缆下料长度精细化计算[J].重庆交通大学学报:自然科学版,2014(5):13-16.

[4] 孙全胜,高红帅.自空间主缆自锚式悬索桥体系转换施工控制[J].重庆交通大学学报:自然科学版,2013(2):112-116.

[5] 张哲.混凝土自锚式悬索桥[M].北京:人民交通出版社,2005.

[6] 严伟飞.江山北关大桥的施工监控[D].大连:大连理工大学,2005.

[7] 高荣堂,李传习,李庭波.平胜大桥自锚式悬索桥基准索股架设的施工控制[J].世界桥梁,2007(1):43-46.

[8] 钟继卫,高建学,王戒躁.大跨度悬索桥基准索股施工控制[J].世界桥梁,2006(2):41-43.

[9] 王锦.混凝土自锚式悬索桥施工仿真分析及吊索张拉优化[D].西安:长安大学,2012.

[10] 牛登辉,周志祥,吴海军,等.自空间自锚式悬索桥体系转换过程的无应力状态控制法[J].重庆交通大学学报:自然科学版,2014(1):21-24.

Main Cable Erection Monitoring of Self-anchored Suspension Bridge

BAODahai,YUANTangchao,LUJiufei

(School of Highway, Chang’an University, Xi’an 710064, China)

The main cable shape control is throughout the entire process of cable systems construction of self-anchored suspension bridge. As the primary part of main cable shape control, the erection of main cable has a direct influence on whether the main cable shape can meet the design requirements. This paper discussed the methods and treatment measures to determine the main cable shape of the key points based on the main cable erection of Zhonghu bridge in Zhejiang province. The calculated results of empty cable shape obtained by standard state analytic method and finite element method had been compared with each other. Finally, for the purpose of ascertain the datum strand shape rapidly and accurately, the influence of unstressed cable length, span, temperature on cable strand sag had been discussed.

bridge engineering；self-anchored suspension bridge；construction control；main cable erection

2015-03-21

包大海(1990-)，男，陕西汉中人，硕士生，主要从事桥梁结构分析方面的研究，(E-mail)1207671163@qq.com

1673-1549(2015)03-0076-04

10.11863/j.suse.2015.03.16

U446

A