变压器电磁耦合模型中动态电感的计算方法

史海涛，王建元，蔡国伟，潘超

(东北电力大学电气工程学院，吉林省吉林市132012)

变压器电磁耦合模型中动态电感的计算方法

史海涛，王建元，蔡国伟，潘超

(东北电力大学电气工程学院，吉林省吉林市132012)

变压器瞬时电感参数计算是备受关注的研究内容。本文结合变压器直流偏磁问题，基于能量平衡原理计算动态电感。建立变压器电磁耦合模型，求解时变非线性磁场，利用局部线性化方法获取系统能量，从而计算动态电感;通过电路求解时域电流，并回馈磁场实现耦合。在此基础上模拟变压器直流偏磁电磁特性，分析在不同直流扰动下动态电感与非线性励磁的对应关系，并总结其规律。搭建实验平台，对比实测数据与计算结果，验证本文所采用方法的准确性。

电磁耦合;动态电感;能量平衡;直流偏磁

1 引言

高压直流输电和电网磁暴灾害中电力变压器发生直流偏磁，励磁饱和导致其电流畸变、谐波含量增加、涡流损耗升高、保护误动作等一系列问题，这些问题都与变压器等电磁设备的电流和电感畸变密切相关［1-3］。因此，结合电流和电感的时变性对变压器直流偏磁进行安全稳定评价和相关保护的设计整定具有十分重要的研究价值［4］。

国内外已有文献对变压器直流偏磁时的电流畸变进行相关研究［5-7］，但对电感的变化并未做深入分析。变压器正常运行时工作在励磁的“拐点”状态，其电感参数可近似为一常数或者变化很小［8，9］。但当变压器直流偏磁时，励磁饱和程度随直流水平升高而加剧，这种情况下电感已发生明显变化，但目前罕有文献关于此问题做出深入研究。

另一方面，变压器电磁耦合的能量过程可以通过外端电路能量和内部磁场能量的相互转化来进行描述和分析［10］，从能量的角度来实现场与路的间接耦合可以在很大程度上降低传统方法建模的复杂程度，进而提高计算效率［11］。文献［12］提出了基于能量原理计算变压器电感参数的方法，能够利用电感映射变压器内部磁场，并通过实验验证了该方法的准确性。文献［13］从能量角度研究利用变压器电感参数设计保护判据的方法，但并未考虑到励磁遭受直流扰动的影响。因此构建物理意义清晰且考虑变压器外端电路和内部磁场的用于电感计算的能量函数，能够考虑在直流扰动下的电路、磁场变化，进而揭示励磁特性与电感参数的内在联系［14-20］。

本文建立变压器电磁耦合模型，将变压器直流偏磁计算分解为非线性磁场模型求解与电路模型计算，以动态电感表征励磁特性，用时域电流描述电路响应，电流和电感作为耦合参数，通过迭代实现电磁耦合。基于能量原理根据电路系统和磁场系统的能量增量计算变压器在不同工作条件下的电感参数，分析变压器直流偏磁时的励磁情况与电感变化的对应关系，并总结其规律。

2 电磁耦合模型

利用电路-磁场耦合模型计算变压器直流偏磁时，动态电感和时域电流为关键耦合参数，分别由三维磁场模型和等效电路模型计算。

单相双绕组变压器的基本电磁关系如图1所示，其中u1为交流激励源，Φ1，2分别为铁心柱体磁通和铁轭旁路磁通，ΔΦ为铁心漏磁通，L、M表示自感与互感，R为电阻。

根据基本电磁关系建立电磁耦合模型。不考虑磁滞效应，棱边有限元法采用矢量磁位A，根据Maxwell得到非线性磁场方程:

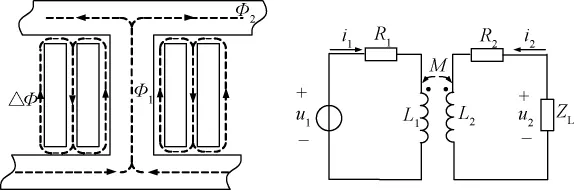
图1 变压器电磁关系Fig．1Electromagnetic relation of transformer

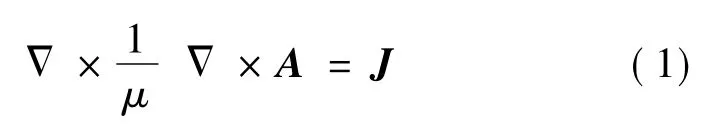
式中，μ为磁导率;J为电流密度。

变压器磁链方程为:

式中，ψ为磁链向量;LS为静态电感矩阵，表示磁链与电流的关系;i为绕组电流向量。

由u=dψ/dt，变压器时域电路微分方程为:

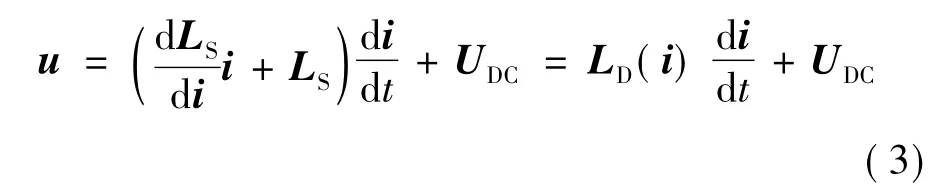
式中，u为交流电压向量;UDC为直流电压向量;LD为动态电感矩阵，表示磁链随激励电流变化的关系，即内部非线性励磁与端口激励的时变特性，需根据磁场模型计算。

电路模型中采用四阶龙格库塔法对式(3)求解，由tk时刻的线圈电流ik计算tk+1时刻ik+1:

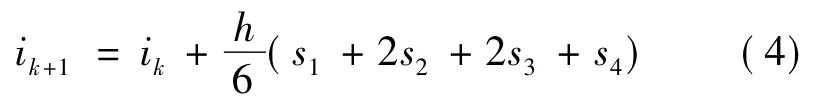
式中，h为步长;s1～s4为步长内的分段计算斜率。

电磁耦合模型的计算步骤如下:

(1)已知变压器磁场模型在某时刻的线圈电流为ik，基于棱边有限元法计算磁场，并通过能量扰动原理计算动态电感LD。

(2)将LD代入电路模型的微分方程，采用四阶龙格库塔法，结合电感参数、直流扰动和交流电源uk+1，计算下一时刻的电流ik+1。

(3)将ik+1回馈磁场模型，进行下一时刻求解。

3 能量平衡原理

根据能量扰动的思想，由系统能量计算动态电感。磁场模型中若已知电流i，代入式(1)求解可得所有棱边上的A，进而计算其他场量，如B和H等。在时域计算的每个时刻，非线性磁场按稳态场求解，磁场能量增量计算采用局部线性化方法。

若单位体积由电流增量δi引起的场量变化为δH、δB，变压器内部系统的磁场能量增量δW2为:

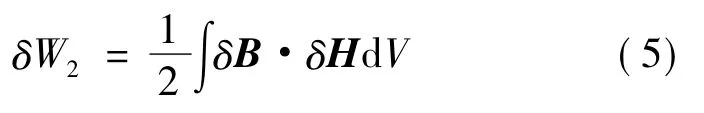
电路模型中当线圈电流增加δi(0≤δ≤1)时，产生磁链δψ，端口电压δu=d(δψ)/dt。外部电源提供的能量增量为dW=δuδidt=δid(δψ)。将电源总能量与动态电感和电流关联，得到变压器电路能量增量δW1为:

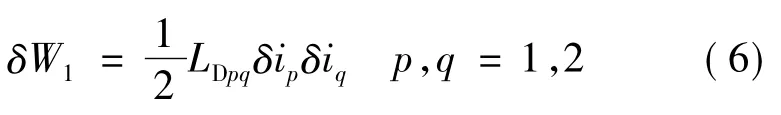
式中，LDpq为动态电感矩阵中各绕组对应电感元素，p、q为一、二次侧绕组编号。

由能量平衡原理，式(5)和式(6)的能量相等，则可计算动态电感LD。

4 算例分析

采用电磁耦合模型计算变压器直流偏磁耦合参数，编译四阶龙格库塔法程序求解时域电路模型，利用ANSYS软件建立变压器的八分之一磁场模型，模型尺寸与实际比例为1∶1，具体参数见表1，磁化曲线见图2。

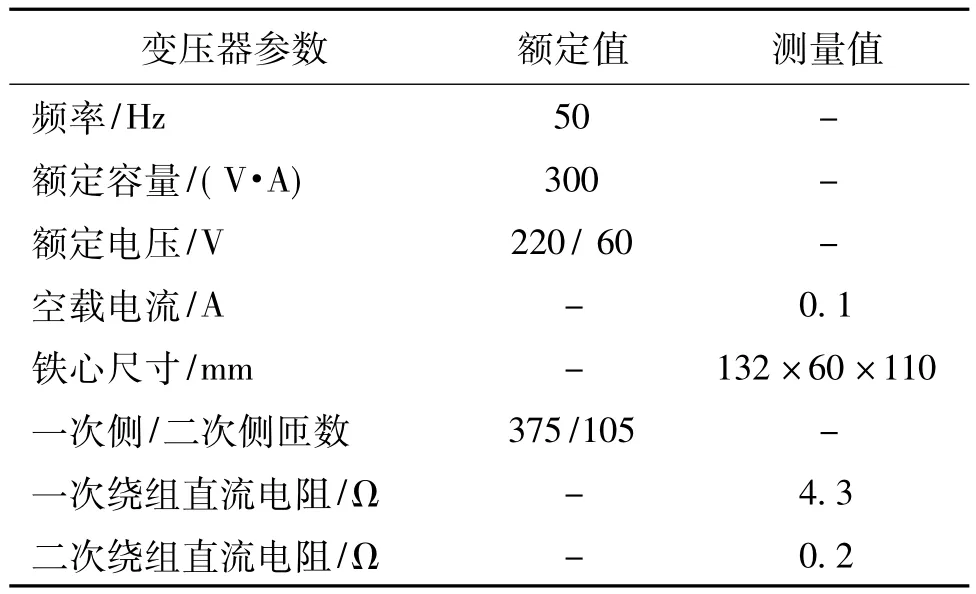
表1 变压器参数Tab．1Parameters of transformer

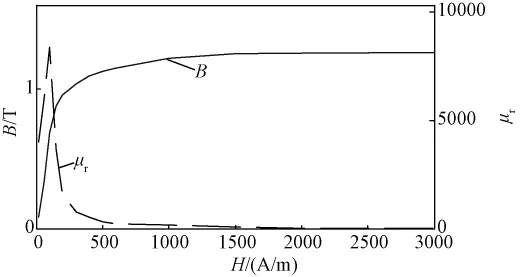
图2 铁心磁化曲线Fig．2Magnetization curves of iron core

4.1 空载运行

计算变压器空载运行时的耦合参数，交流电压有效值U1RMS=50V和220V时的结果如图3所示。

图3 变压器空载运行时耦合参数波形Fig．3Parameters of transformer in no-load operation

图3(a)中i1为一次侧电流，空载时励磁电流ie可近似为i1。i1与励磁非线性有关，其波形的峰谷位置表示变压器励磁处于饱和状态，过零点附近表示励磁不饱和。迭代计算结果受初值影响存在振荡过程，如图3(a)中的区域I;分析时选取计算稳定后的结果，如图3(a)中的区域II。当交流电压有效值U1RMS为50V时，变压器励磁变化范围处于不饱和区(线性区)，i1波形近似呈正弦波;提高变压器两端电压，励磁逐渐趋于饱和，当U1RMS=220V时，励磁状态在饱和与不饱和间变化，i1呈尖顶波形。图3 (b)中L1为一次侧动态电感，L1的波峰与波谷位置分别表示励磁处于不饱和状态与饱和状态。当电压较低时，由于励磁不饱和，L1波动范围较小;当电压较高时，励磁状态变化明显，L1波动范围较大。由图3可以确定电流、电感变化与励磁非线性的对应关系。无直流时，i1与L1的波形在正、负半周对称。i1接近零值时，铁心励磁处于不饱和区，L1数值趋于最大;当ie趋于各半周内的极值时，铁心励磁饱和程度逐渐加深，L1数值趋于最小。

4.2 直流偏磁

计算变压器空载直流偏磁时的耦合参数，U1RMS=220V，空载电流I0=0.1A，IDC=0、50%I0、100%I0时的结果如图4所示。

图4 变压器直流偏磁时耦合参数波形Fig．4Parameters of transformer in DC bias

当存在直流时，L1受直流水平影响，波形在正负半周不对称，随着直流电流增大，变压器励磁饱和程度加深，i1畸变严重，L1波形在正负半周的不对称程度加剧。

5 实验验证

实验变压器型号为BK300，如图5所示，参数见表1。

图5 实验变压器Fig．5Transformer for experiment

设计低通滤波和时域差分模块对变压器进行测量，无直流时的电流和电感波形如图6所示。

从图6中不难看出，实验数据中主要的谐波来源于电流i1，为了提高计算准确性，采用低通滤波方法减少高频分量的影响，如图6(a)所示。根据式(3)对电流进行时域差分变化，并结合电压同步数据，可以得到电感参数的瞬时波形，如图6(b)所示。无直流时，i1、L1的变化情况及对应关系与仿真计算基本一致。

图6 变压器空载运行220V时参数波形Fig．6Parameters of no-load transformer under 220V

当直流分量IDC=50%I0时的电流和电感波形如图7所示。

由图7可知，变压器直流偏磁时i1、L1的波形畸变，这与图4结果基本相同。对计算和实验结果进行深入分析，由于模型未考虑磁滞，根据u→dψ/dt→dΦ/dt→B～H→i1的电磁耦合关系，仿真电流i1为对称波，而实测电流为非对称波，两者主要在ie过零时存在误差，如图8所示。分析误差原因，可能是由于磁滞效应所导致，说明不考虑磁滞对变压器不饱和励磁时的计算精确性产生一定影响。随着直流升高，变压器励磁饱和程度加深，i1畸变加剧，磁滞引起的误差变小。从实验电流i1中滤除高次谐波分量，并与仿真计算的电流有效值IRMS比较，结果见表2，其中变压器运行方式为空载。

另外，由于低通滤波和时域差分模块存在一定的积累误差，导致实际测量得到的瞬时电感波形并不是理想的平滑波，因此与计算对比存在误差，但其变化规律与仿真结果基本一致。

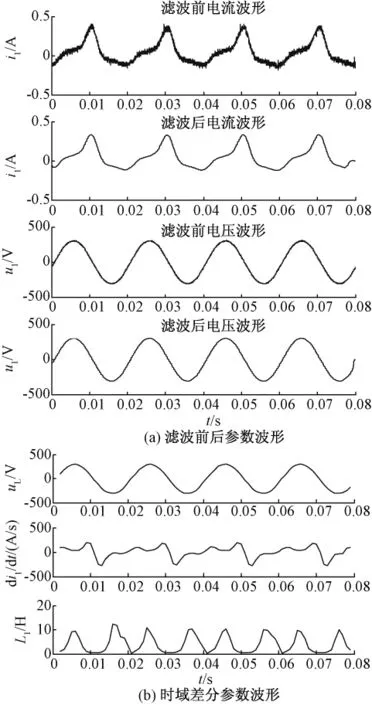
图7 变压器空载运行220V时参数波形(IDC=50%I0)Fig．7Parameters of no-load transformer under 220V(IDC=50%I0)

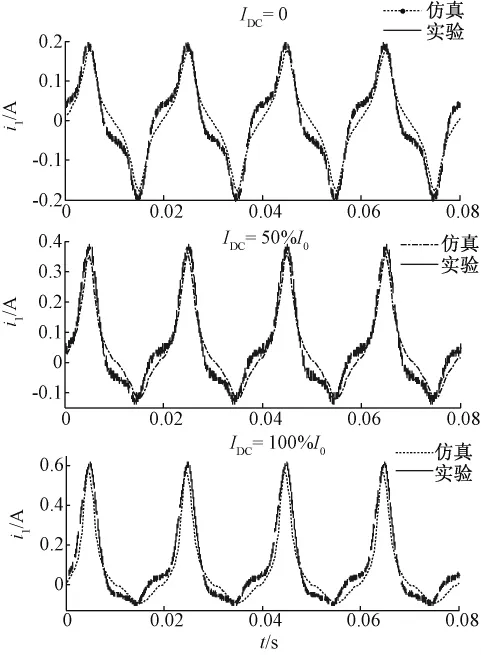
图8 变压器空载直流偏磁实验与计算电流Fig．8Currents of DC-biased transformer with no load

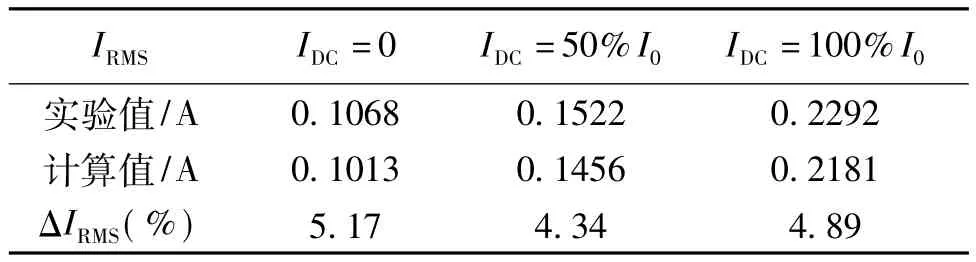
表2 计算电流与实验测量的相对误差Tab．2Errors of current between compute and test

仿真结果与实验数据表明，变压器未发生直流偏磁时电感、电流波形在每周期规则波动，且变化规律与变压器励磁特性对应;在直流扰动下，变压器励磁饱和程度加深，电感、电流波形出现畸变，随着直流偏置水平升高，畸变程度加剧。

变压器电感参数在直流偏磁时波形畸变，这与传统系统电感参数变化存在明显区别，其主要原因是由于变压器励磁非线性所导致。通过理论推导、仿真计算及实验测量对电流、电感参数受直流扰动的变化规律进行分析和归纳，在此基础上可以进一步开展变压器直流偏磁时涡流损耗等问题的研究。

6 结论

利用变压器电磁耦合模型计算其电磁特性，研究直流偏磁时的动态电感，得出以下结论:

(1)变压器电磁耦合模型将非线性磁场有限元法计算与时域电路龙哥库塔法求解迭代耦合，能够利用时域电流和动态电感参数有效模拟变压器的励磁变化情况。

(2)变压器在无直流扰动时，时域电流和动态电感波形在每周期正、负半周对称，并与励磁饱和状态对应;发生直流偏磁时励磁饱和程度加深，电流、电感畸变，并随着直流水平升高，畸变程度加剧，该规律对于大型变压器同样适用，从而可为大型变压器直流偏磁运行特性分析和保护设计提供可行途径。

［1］C M Liu，L G Liu，R Pirjola．Geomagnetically induced currents in the high-voltage power grid in China［J］．IEEE Transactions on Power Delivery，2010，24(4): 2368-2374．

［2］郑涛，陈佩璐，刘连光，等(Zheng Tao，Chen Peilu，Liu Lianguang，et al．)．计及直流偏磁的电流互感器传变特性对差动保护的影响(Transferring characteristics of current transformer affected by DC magnetic bias and its impact on differential protection)［J］．电力系统自动化(Automation of Electric Power Systems)，2012，36(20):89-93．

［3］赵小军，李琳，程志光，等(Zhao Xiaojun，Li Lin，Cheng Zhiguang，et al．)．应用谐波平衡有限元法的变压器直流偏磁现象分析(Analysis of the DC bias phenomenon in transformers based on harmonic-balanced finite element method)［J］．中国电机工程学报(Proceedings of the CSEE)，2010，30(21):103-108．

［4］索南加乐，张健康，张军民，等(Suonan Jiale，Zhang Jiankang，Zhang Junmin，et al．)．交直流混联系统对变压器保护性能的影响及解决措施(The adverse impacts on transformer protection performance by hybrid ACDC transmission grid system and counter-measures)［J］．电力系统自动化(Automation of Electric Power Systems)，2010，34(3):101-106．

［5］李晓萍，文习山(Li Xiaoping，Wen Xishan)．三相五柱变压器直流偏磁计算研究(DC bias computation study on three-phase five limbs transformer)［J］．中国电机工程学报(Proceedings of the CSEE)，2010，30 (1):127-131．

［6］李泓志，崔翔，卢铁兵，等(Li Hongzhi，Cui Xiang，Lu Tiebing，et al．)．变压器直流偏磁的电路-磁路模型(Electric circuit and magnetic circuit combined model of DC biased power transformer)［J］．中国电机工程学报(Proceedings of the CSEE)，2009，29(27):119-125．

［7］Shu Lu，Yilu Liu．FEM analysis of DC saturation to assess transformer susceptibility to geomagnetically induced currents［J］．IEEE Transactions on Power Delivery，1993，8(3):1367-1376．

［8］马静，王增平，王雪(Ma Jing，Wang Zengping，Wang Xue)．基于等效瞬时漏电感的变压器保护原理(Novel principle of power transformer protection based on equivalent instantaneous leakage inductance)［J］．电力系统自动化(Automation of Electric Power Systems)，2006，30(23):64-68．

［9］焦在滨(Jiao Zaibin)．基于励磁支路参数的变压器保护新原理(New transformer protection principle based on the parameters of the excitation branch)［D］．西安:西安交通大学(Xi’an:Xi’an Jiaotong University)，2008．

［10］S L Ho，S X Niu，W N Fu，et al．A power-balanced time-stepping finite element method for transient magnetic field computation［J］．IEEE Transactions on Magnetics，2012，48(2):291-294．

［11］X J Zhao，L Li，J W Lu，et al．Characteristic analysis of the square laminated core under dc-biased magnetization by the fixed-point harmonic-balanced FEM［J］．IEEETransactions on Magnetics，2012，48(2):747-750．

［12］N A Demerdash，R Wang．Theoretical and numerical difficulties in 3-D vector potential methods in finite element magnetostatic computations［J］．IEEE Transactions on Magnetics，1990，26(5):1656-1658．

［13］王雪，王增平(Wang Xue，Wang Zengping)．基于有限元法的变压器电感参数计算方法研究(An investigation on transformer inductance calculation based on finite element method)［J］．电力系统保护与控制(Power System ProtectionandControl)，2009，37 (24):11-14．

［14］M V F da Luz，J V Leite，A Benabou，et al．Three-phase transformer modeling using a vector hysteresis model and including the eddy current and the anomalous losses［J］．IEEE Transactions on Magnetics，2010，46(8):3201-3204．

［15］Zhigang Zhao，Fugui Liu，Zhiguang Cheng，et al．Measurements and calculation of core-based B-H curve and magnetizing current in DC-biased transformers［J］．IEEE Transactions on Applied Superconductivity，2010，20 (3):1131-1134．

［16］林湘宁，刘沛，高艳(Lin Xiangning，Liu Pei，Gao Yan)．基于数学形态的电流互感器饱和识别判据(A novel method to identify the saturation of the current transformer using mathematical morphology)［J］．中国电机工程学报(Proceedings of the CSEE)，2005，25(5): 44-48．

［17］梁振光，唐任远(Liang Zhenguang，Tang Renyuan)．采用场路耦合的三维有限元法分析变压器突发短路过程(Fault simulation power transformers using 3D finite element model coupled to electric circuit equations)［J］．中国电机工程学报(Proceedings of the CSEE)，2003，23(3):137-140．

［18］谢若冰，陈桥夫，康崇皓，等(Xie Ruobing，Chen Qiaofu，Kang Chonghao，et al．)．基于组合式场路耦合法的多绕组变压器建模与阻抗参数设计(Modeling and impedance parameter design for multi-winding transformer based on combined field-circuit coupled method)［J］．中国电机工程学报(Proceedings of the CSEE)，2009，29(9):104-111．

［19］Chishan Yu．Detection and correction of saturated current transformer measurement using decaying DC components［J］．IEEE Transactions on Power Delivery，2010，25 (3):1340-1347．

［20］Jawad Faiz，Saeed Saffari．Inrush current modeling in a single-phase transformer［J］．IEEE Transactions on Magnetics，2010，46(2):578-581．

Dynamic inductance computation in electromagnetic coupled model of transformer

SHI Hai-tao，WANG Jian-yuan，CAI Guo-wei，PAN Chao
(School of Electrical Engineering，Northeast Dianli University，Jilin 132012，China)

Computation of the instant inductance in transformer is concerned as a hot topic．Considering the DC-biasing problem，the dynamic inductance of transformer is computed based on the energy-balanced principle．The electromagnetic coupled model is built．And the time-varying electromagnetic computation of transformer is decomposed into nonlinear magnetic and time-domain circuit．The dynamic inductance can be calculated from the system energy by magnetic solving，while the time-domain current is computed by iteration of electrical circuit．By this method，the electromagnetic characteristics of DC-biased transformer are simulated．The relationship between dynamic inductance and nonlinear excitation is analyzed under different DC disturbances．Experiment is carried out to measure the parameters．Comparing the computed results with the experimental data shows consistency．And the proposed method is valid for the related analysis for electromagnetic devices such as transformer．

electromagnetic coupling;dynamic inductance;energy balance;DC bias

TM74;TM41

A

1003-3076(2015)08-0069-06

2014-05-13

长江学者和创新团队发展计划资助项目(IRT114)

史海涛(1971-)，男，吉林籍，实验师，硕士，研究方向为电力系统稳定;王建元(1971-)，男，陕西籍，教授，硕导，长期从事电力系统稳定分析的研究。