基于Simulink的风力机变桨距机构的设计与仿真

杨 江 王雅萍 朱目成 赵冬梅 姜 翔

(西南科技大学制造过程测试技术教育部重点实验室 四川绵阳 621010)



基于Simulink的风力机变桨距机构的设计与仿真

杨 江 王雅萍 朱目成 赵冬梅 姜 翔

(西南科技大学制造过程测试技术教育部重点实验室 四川绵阳 621010)

采用叶素动量理论确定工作条件的改变对应桨距角的变化，从理论上提高桨距角的控制精度，进行了风力机变浆距机构设计。通过仿真验证了设计的正确性，同时得到了桨距角匀速转动时液压缸驱动活塞的位移、速度、加速度的变化规律。

变桨距机构 叶素动量理论 Simulink 驱动特性

随着风力发电技术的不断成熟，变桨距控制型风力发电机组以其优越的性能得到重视，变桨距控制不仅可以使机组在低风速下最大程度地捕获风能，而且可以使机组在高风速时输出功率在额定功率附近，不至于损坏机组[1]。对于大型风力机，考虑到驱动力较大，而且控制精度和灵敏度要求较高，通常采用电机驱动的齿轮来控制，其控制计算复杂[2]，而对于小型风力机，从经济性和结构角度来考虑齿轮传动不再适合，结构简单的曲柄滑块机构更加适合，而且通过设计优化完全可以满足控制精度的要求。

本设计以叶素动量理论为控制依据而非传统的经验公式[3]提高控制精度，采用滑块驱动的曲柄滑块机构作为变桨距的执行机构，采用液压驱动控制系统。

1 变桨距调节原理

1.1 叶素最佳运转原理

已知叶轮旋转的角速度为ω，叶片半径方向[r,r+dr]处叶素的圆周速度u=rω，通过风轮时气流的绝对速度v、该叶素的圆周速度u及相对于翼型的气流速度ω之间的关系为v=ω+u。

θ为叶素倾角，β为叶素安装角(桨叶角)，α为攻角。

根据叶素动量理论，得出理想情况下气流与叶片角之间的关系：

θ=α+β

(1)

令升阻比e=C1/Cd，得到叶素的理论空气动力效率为[4]：

(2)

由上式可以看出，翼型的升阻比e越高，叶素的空气动力学效率越高，因此叶素冲角α为最佳冲角时，叶素的效率最高。

对于风力机叶片，叶素是其工作单元，因此只有在叶素获得最大的效率前提下，叶片才能获得最大的效率，对于风速的改变，气流角发生变化，这时叶素安装角需同步变化以使攻角保持不变。

根据Glauert漩涡理论得到叶素在最佳工作条件下，叶素倾角θ与叶尖速比λ之间的关系如图1所示。对于给定的调速范围，便可以得到叶素倾角的变化，从而得到桨距角的变化范围。

图1 叶尖速比对应叶素倾角的关系Fig.1 Relationship between lift drag ratio and angle of flow

1.2 风力机开关机

在风力机开机之前，桨叶的桨距角为90°，风轮为静止状态，这时气流对桨叶不产生转矩。需要开机时，控制桨叶向β=0°方向(即顺桨位置)变化，直到气流对桨叶产生一定的攻角，风力开始转动起来[5]；当风力机需要停车关机时，桨叶的桨距角向β=90°方向变化，此时，叶片就变成了一块阻尼板，为风力机提供制动转矩。

2 变桨距机构设计

机械执行机构采用对置曲柄滑块机构。采用液压驱动控制系统，拟选择曲柄r2=100 mm，连杆r3=220 mm，变桨距机构设计如图2所示。对于桨叶两个极限位置分别对应的活塞位置如图所示，这与传统设计有点差别，将在后面说明。

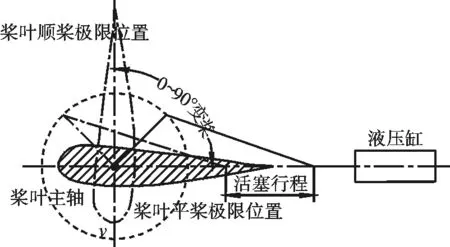
图2 变桨距机构原理图Fig.2 The schematic diagram of pitch-regulated mechanism

3 机构运动学分析

变桨距机构的矢量环如图3所示[6]。

图3 曲柄滑块机构的矢量环Fig.3 The vector ring of slider-crank mechanism

r2+r3=r1

(3)

式中：r1-液压缸推杆平移运动矢量；r2-曲柄运动矢量；r3-连杆运动矢量。

将矢量分解到x和y坐标轴上得到机构位移方程[7]：

(4)

对(4)式求导得机构的速度方程：

(5)

对(5)式求导得机构的加速度方程：

(6)

对于给定的初始条件，通过上式求解，可得到机构任意时刻的运动参数。

4 机构的Simulink仿真

4.1 风力机开桨机构仿真

开桨时，我们以桨叶匀速转动建立Simulink仿真模型[8-10]，如图4所示。

分析可知桨叶角度行程为90°，由式(4)计算得到r1与θ2的对应关系，分析可知在θ2=45°～135°时r1与θ2近似成线性关系，为了方便控制选用其为桨距角变化范围。

在开桨状态曲柄处于左极限位置，因此初始条件为：ω2=-5°/s，θ2=135°，θ3和r1由计算得到，当仿真时间为18 s时，仿真结果如图5所示。

由图5可得到液压缸的活塞行程为142 mm。

图4 Simulink仿真建模Fig.4 Simulating and modeling by Simulink

图5 桨叶匀速运动时活塞的运动特性曲线Fig.5 Kinetic characteristic curve of piston under the condition of uniform rotation pitch angle

4.2 紧急关机机构仿真

当风力机出现紧急情况时如零件损坏，此时就需要桨叶角快速从0°切换到90°，为风力机提供最大的制动力矩，使风力机快速停机以保护机组构件。

令桨叶转动角速度为：

(7)

令t0=6.28 s，得到参数A，B后计算桨叶角转动的角加速度作为仿真的输入。仿真初始条件θ2=45°，t=t0。紧急关机下的仿真模型如图6所示，仿真结果如图7所示。

图6 紧急关机下Simulink仿真建模Fig.6 Simulating and modeling by Simulink under the conditon of emergency shutdown

图7 紧急关机活塞运动特性曲线Fig.7 Kinetic characteristic curve of piston under the condition of emergency shutdown

4.3 变风速机构仿真

对于变桨距恒速发电机，设计额定风速为5 m/s，额定叶尖速比为5，当风速在3.5～8 m/s内变化时，可得到叶尖速比的变化，由图1得到叶素倾角θ，这里选取NACA4412翼型，最佳攻角为α=4.5°[11]。通过计算得到对应角度关系如表1所示。

表1 风速对应各参数值Table 1 The parameters of wind speed

通过Simulink仿真可得到风速变化对应液压缸活塞位移的关系如图8所示。

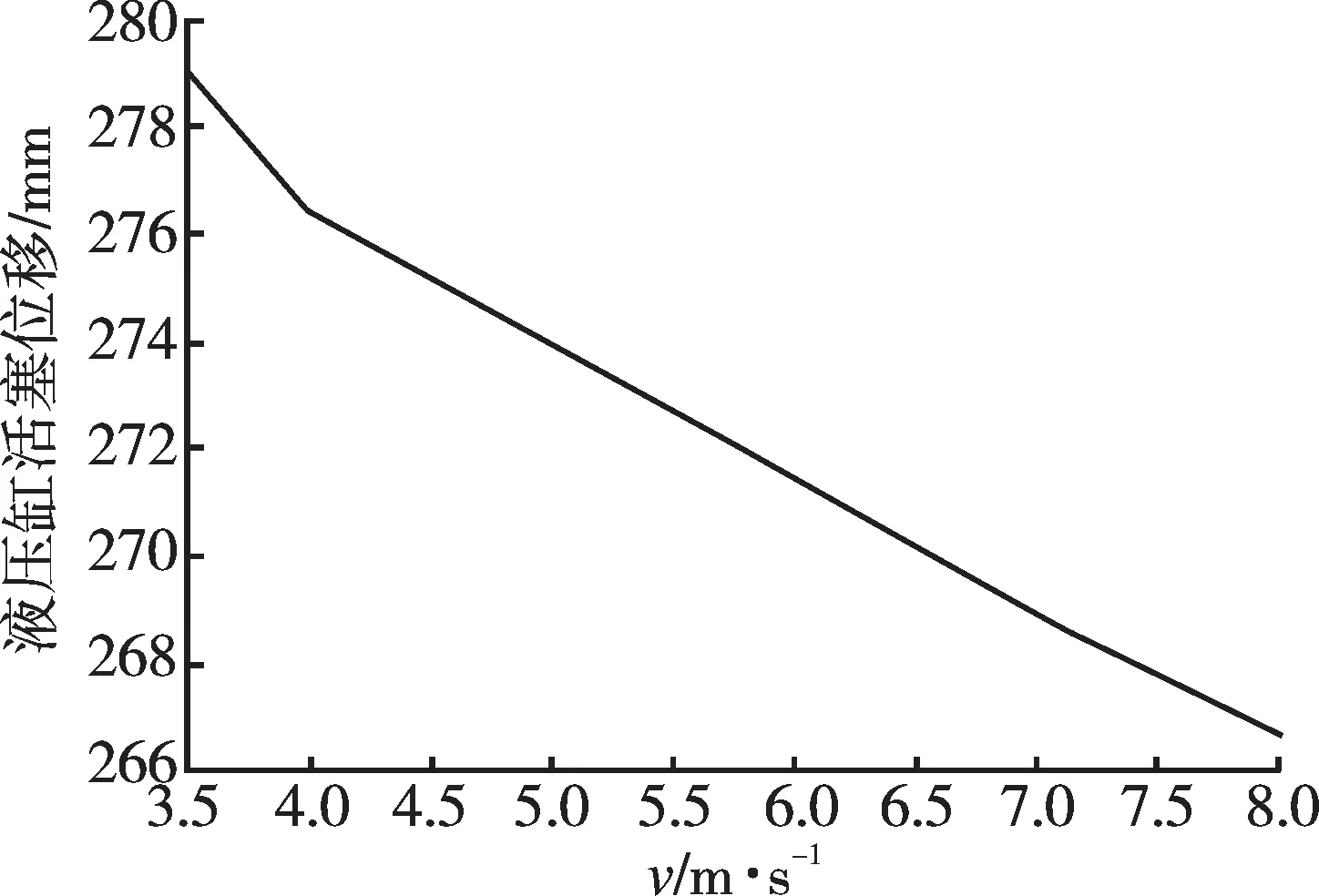
图8 活塞位移随风速的变化Fig.8 The piston displacement along with the change of wind speed

在获得各风速桨叶的工作情况下，通过Matlab仿真可得到叶素不同工况下的效率，采用变桨距和定桨距控制的叶素效率如图9所示。

图9 叶素效率比较Fig.9 Airfoil efficiency comparison

4.4 桨距控制精度分析

桨距角对应翼型的最佳冲角，对风力机最大效率影响显著，因此，其定位精度要求较高。

定位精度的计算：

(7)

通过Matlab编程[12]计算得到桨叶角的定位精度随桨距角的变化如图10所示。

由图10可知，桨叶在桨距角为0～50°之间的定位精度较高。该机构桨叶桨距角工作在0～10°的范围，获得较高的定位精度，因此该机构的设计比较合理。这也是选择桨叶极限位置对应活塞位置的依据。

设计变桨距调节的桨距角定位精度为0.1°，在桨距角为0～10°的工作范围内，定位精度最小为1.67 mm/°，液压缸活塞的定位精度为：1.67×0.1=0.167 mm。因此，在选取驱动液压缸时，液压缸的行程大于142 mm，定位精度在高于0.167 mm的情况下便能满足桨距角调节要求。

图10 定位精度随桨距角的变化曲线Fig.10 Positioning accuracy along with the change of angle of pitch

5 结论

采用叶素动量理论得到桨叶来流风速的改变对应桨距角的变化，为机构控制提供了精确的数据，从理论上提高了桨距角的控制精度，为风力机变桨距机构的设计提供了一种新的方法。对机构通过Matlab/Simulink进行仿真，可知采用该变桨距机构对叶素效率有明显的提高，从而验证了设计的正确性，同时通过仿真得到满足机构运行条件的输入数据。

[1] 赵玉清.风力机最大能量捕获及功率稳定性研究[J].机械管理开发，2011,121(3):52-53.

[2] DOLAN B, ASCHEMANN H.Nonlinear Control for Load Reduction on a Variable Speed Pitch Regulated Wind Turbine[C].IEEE Transactions on Energy Conversion,2013.

[3] 韦徵，陈冉，陈家伟.基于功率变化和模糊控制的风力发电机组变速变桨距控制[J].中国电机工程学报，2011,31(17):121-126.

[4] 郭新生.风能利用技术[M].北京：化学工业出版社，2007.

[5] 孙涛.兆瓦级风力机变桨距控制及其执行机构优化设计[D].兰州：兰州理工大学机电工程学院硕士论文，2010.10-14.

[6] YAO Xing-jia,SHAN Guang-kun,SU Dong-hai.Study on Variable Pitch System Charcteristics of Big Wind Turbine[C].International Technology and Innovation Conference,2006.

[7] 李志梅，魏本建，赵东标.风力发电机组电动变桨距机构设计与仿真[J].机械设计与制造，2008,(4):57-59.

[8] [美]约翰·F·加德纳.机构动态仿真：使用MATLAB和Simulink[M].西安：西安交通大学出版社，2002.

[9] 张德丰.MATLAB/Simulink建模与仿真实例讲解[M].北京：机械工业出版社，2010.

[10] 刑钢，郭威.风力发电机组变桨距控制方法研究[J].农业工程学报，2008,24(5):181-186.

[11] 赖旭，何伟，胡雄.风力机翼型及叶片气动性能数值模拟[J].武汉大学学报，2010,43(3):273-277.

[12] 刘勍，温志贤.MATLAB基础及应用[M].南京：东南大学出版社，2011.

Design and Simulation of Pitch-regulated Mechanism of Wind Turbine Based on Simulink

YANG Jiang, WANG Ya-ping, ZHU Mu-cheng ZHAO Dong-mei, JIANG Xiang

(KeyLaboratoryofTestingTechnologyforManufacturingProcess,MinistryofEducation,SouthwestUniversityofScienceandTechnology,Mianyang621010,Sichuan,China)

The theory of blade element momentum is used to determine the pitch angle change under working conditions, rather than empirical formula. The control accuracy was improved in theory, and based on this,pitch-regulated mechanism of wind turbine was designed. Through simulation, the correctness of the design was veryfied and the drive displacement, velocity and acceleration are achieved under the condition of uniform rotation pitch angle.

Pitch-regulated mechanism; Blade element momentum; Simulink; Drive performance

2014-09-27

四川省科技支撑计划项目(2014GZX0009)。

杨江(1989—)，男，硕士研究生，研究方向为机械设计与制造。E-mail:beseman@sina.com

TK83；TM614

A

1671-8755(2015)01-0090-05