隧洞检修车转向机构优化及动力学分析

胡友安，周军，宋戈

（河海大学机电工程学院，江苏常州 213022）

隧洞检修车转向机构优化及动力学分析

胡友安，周军，宋戈

（河海大学机电工程学院，江苏常州 213022）

对隧洞检修车转向机构的工作原理作了具体分析，并以转向力矩为研究对象，基于遗传算法，使用Matlab软件对设计的转向梯形机构进行了参数优化，同时使用大型多体系统动力学仿真分析软件（ADAMS）对转向机构进行了动力学仿真分析，得出转向机构工作过程中各参数变量（转向角、转向力矩）随时间的变化曲线，并对曲线进行了分析，进而提出合理的改进方案，通过仿真结果可以知道各参数对机构工作性能的影响，有利于选择优化参数，从而设计出合理的转向机构。

转向机构；遗传算法；Matlab；ADAMS；仿真

0 引言

隧洞检修车是隧洞检修中使用的大型机械设备，主要用于水利水电隧洞内的清理与检修作业，其主体是板梁结构。采用隧洞检修车可极大地提高隧洞检修施工的工作效率，降低检修人员的劳动强度。本文以水利水电隧洞检修车作为研究对象，根据遗传算法的理论，利用Matlab软件，对检修车转向机构各项参数进行优化，并利用大型多体系统动力学仿真分析软件（ADAMS）对优化后的转向机构进行了动力学仿真分析，观察仿真曲线可知各参数对机构工作性能的影响，有利于优化参数，有利于设计出更合理的机构，实现智能设计。

1 隧洞检修车的整体结构

隧洞检修车主销中心距为4.000 m，轴距为4.500m，车架高为2.722 m。工作隧洞的直径为8.000m，最大坡度角为50°。由于检修车工作环境复杂、恶劣，工作强度大［1］，因此选用整体式梯形机构作为车辆的转向机构。门架底部设置有4个车轮，可在隧洞内行走。隧洞检修车车体由车身（含行走驱动机构、行走转向机构）、检修平台（含电动翻转装置）、电气系统（含照明系统、操纵装置、通信装置）等组成，车体结构如图1所示。

检修车在隧洞中沿隧洞轨迹运行，车辆沿斜坡上行时，由卷扬机拖动，下行时在自重作用下移动，并由卷扬机控制其下行速度；在水平隧洞内由行走驱动机构驱动检修车行走。卷扬机拖动时驱动机构离合器为常开，驱动机构驱动行走时卷扬机同时进行钢丝绳的收放。

图1 隧洞检修车车体结构

2 隧洞检修车转向机构系统分析

梯形转向机构由车架、转向横拉杆、转向梯形臂、转向传动等装置组成。整体式梯形转向机构的设计遵循阿克曼原理，这种设计方式简单有效，多应用于工作环境恶劣、工作强度大的工程车辆。阿克曼原理的基本观点是汽车无论是在直线还是转弯行驶过程中，每个车轮的运动轨迹都必须完全符合它的自然运动轨迹，从而保证轮胎与地面间为纯滚动而无滑动。阿克曼原理如图2所示。

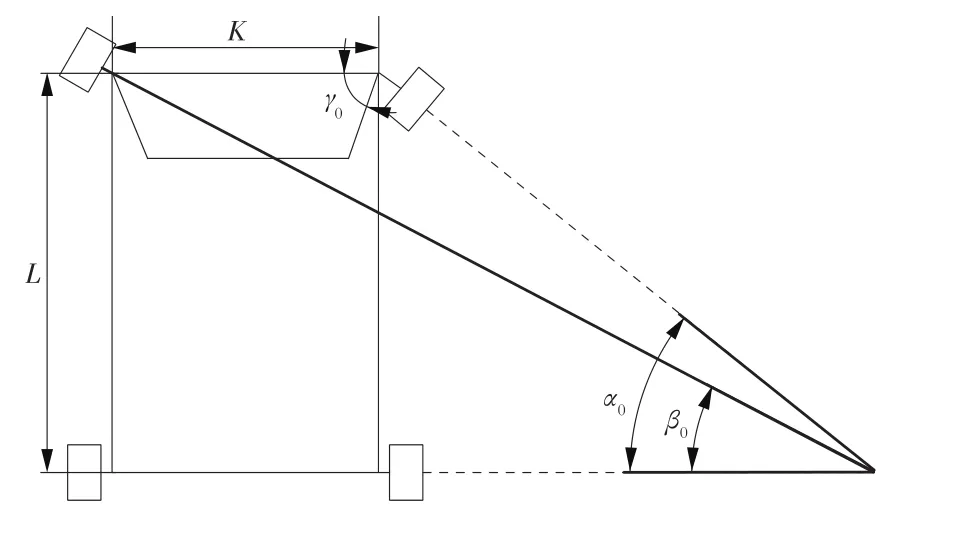
图2 阿克曼原理示意

由图2可以看出，满足阿克曼原理即满足公式［2-3］：

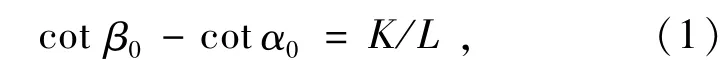
式中：K为主销中心距，mm；L为轴距，mm；β0为外侧车轮理想转角，（°）；α0为内侧车轮理想转角，（°）。则内轮转角与外轮转角的函数关系为

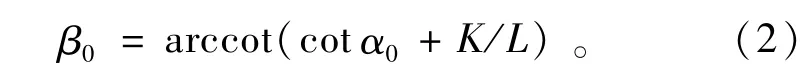
由检修车设计参数可知，车辆前轮主销中心距K＝4000mm，轴距L＝4 500mm。利用Matlab中的线性绘图命令和函数文件编程，可以对上述模型求解，得到隧洞检修车理想内、外轮转角关系的理论特性曲线如图3所示。

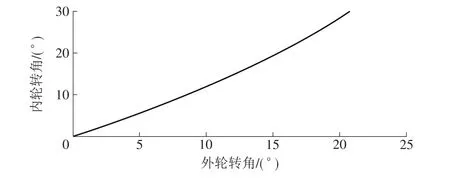
图3 检修车转向机构理想内、外轮转角关系

然而实际的转向机构是由转向梯形机构近似地实现图3的理论特性，而不是精确满足理想内、外轮转向角关系，只能以足够的精度接近转向理论特性。因此，需要对转向机构的参数进行优化，得到转向特性曲线尽可能接近理想转向特性曲线的设计参数，从而减小车轮与地面的滑动摩擦。

3 转向机构参数优化设计

3.1 目标函数建立［4-5］

目前已知参数为车辆前轮主销中心距K＝4000 mm，轴距L＝4 500mm，最小传动角δmin＞40°，主销内倾角0°～3°，主销后倾角0°～1.5°，前轮外倾角0°～1°，内侧车轮极限转角40°。

根据实际情况，该问题的目标函数、约束条件、变量数目过于复杂，为节省时间和资源，在满足设计要求的前提下作如下2点基本假设：（1）忽略轮胎弹性侧偏等影响，将车轮视为刚性体；（2）转向梯形为平面四连杆机构，忽略前轮定位参数的影响。

基于以上2点基本假设，梯形转向机构的主要参数包括转向梯形臂m，梯形底角γ0，外转向轮极限转角αmax，最小传动角δmin，车辆主销中心距K，轴距L，即

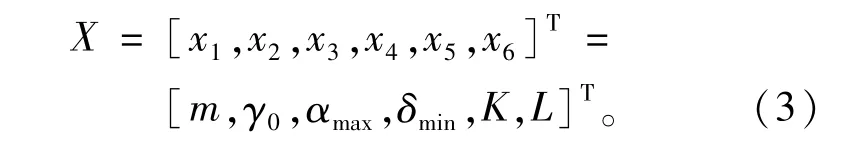
图4为转向梯形机构示意图，由图4可知，当内侧车轮实际转角为α时，通过转向梯形所能获得的外侧转向车轮的实际转角为β′。根据前面所做的2个基本假设，可推导出β′与α的关系为

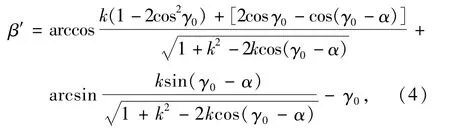
式中：γ0为转向梯形设计底角，（°）；m为转向梯形臂长，mm；K为车辆主销中心距，mm；k＝m／K为梯形臂长与车辆主销中心距之比。

图4 梯形转向机构示意

转向梯形四连杆机构的设计应使外侧车轮实际角度与理论角度相差最小，一般取内侧车轮转角αi对应的实际外侧车轮转角β′（αi）与理想外侧车轮转角β（αi）之间相对误差的加权求和作为评判参数优劣的目标函数，即

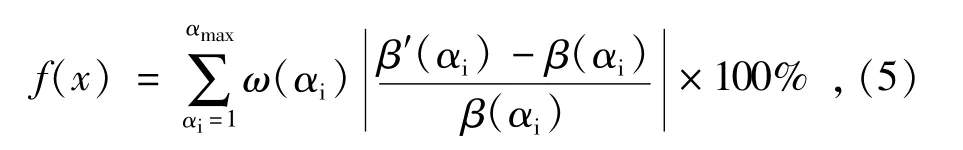
式中：x为设计变量；αmax为车辆内侧车轮最大转角，（°）；ω（αi）为加权系数，取值范围为

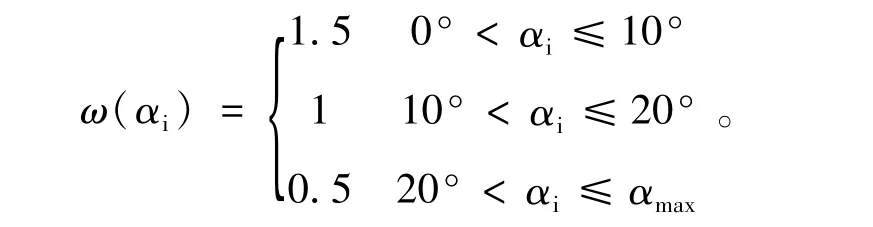
ω（αi）是内轮转角的函数，考虑到车辆常用转角αi≤20°，且在20°以内使用更频繁，因此其权应大，使实际关系与阿克曼关系的偏差小，以减小高速行驶时轮胎的磨损。

将式（4）代入式（5）得到目标函数解析式

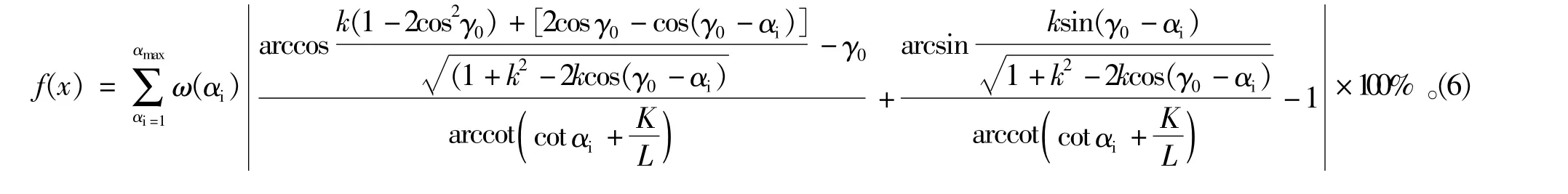
对式（6）进行分析可知，影响目标函数结果的参变量有车辆主销中心距K，转向梯形摇臂长度m，以及转向梯形设计底角γ0。由于实际情况中，车辆主销中心距受车体宽度严格限制，故用梯形臂比k＝m／K来代替m，K这2个参数。由此得到实际优化中的设计变量x为梯形臂比k与转向梯形设计底角γ0，表示为x＝［k，γ0］。

3.2 约束条件建立

由四连杆基本原理可知，四连杆机构的最小传动角的大小关系到机构的运行稳定性和受力特性，且传动角过小会产生自锁现象，因此，设计时最小传动角的理论值应大于40°，而最小传动角亦成为优化设计时的最主要约束。

如图4所示，在△abd1中和△ac1d1中，由余弦定理得

将式（7）、式（8）联立得

因此

式中：β′为α为αmax时β′max的取值。

根据转向梯形的设计经验，梯形臂比k和转向梯形底角γ0取值范围为

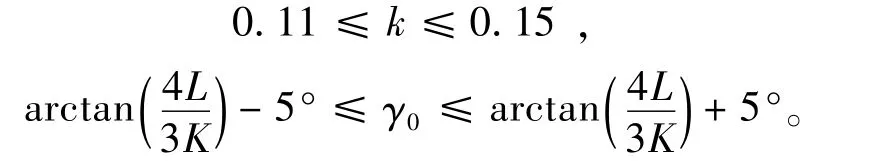
3.3 优化模型建立

由上文各个优化模型整理可以得到同一目标函数的转向机构总体优化模型。

目标函数方程为

约束条件方程g（x）＝

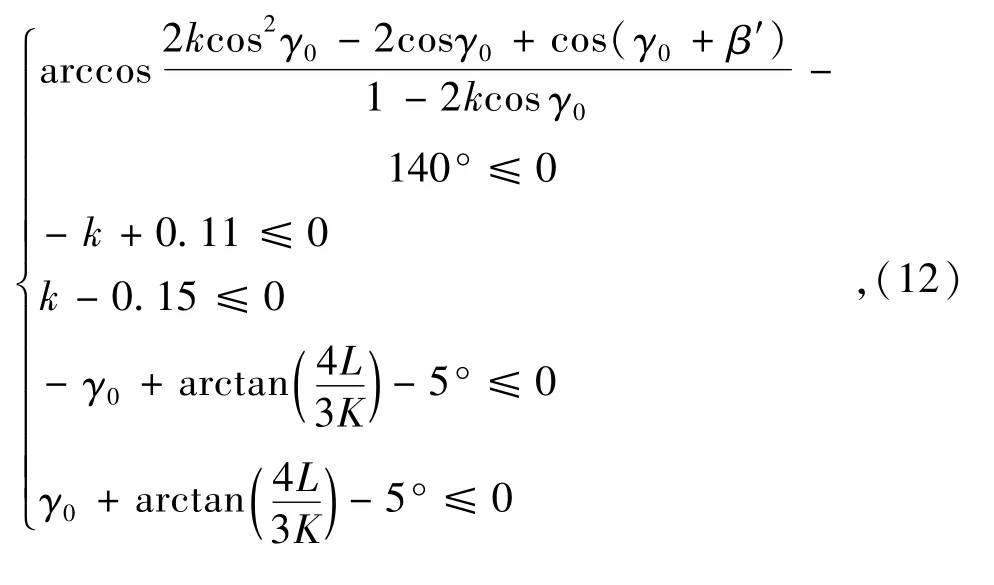
3.4 优化模型求解与结果分析

遗传算法是优化设计中的一种常用算法，对求解简单四连杆模型问题有速度快、精度高的优点。遗传算法在给定初始值、目标函数与约束条件的限制下，通过产生初始种群、个体适应度计算、选择与交叉以及子代个体的产生等步骤，得出初始值附近的目标函数局部最优解［6］。Matlab软件中集成了遗传算法工具箱，本文选择常用的遗传算法（GA）函数工具进行优化求解，首先根据给定初始转向梯形臂长568mm，转向梯形底角55°，将3.3中的转向机构总体优化模型输入软件中，在进行迭代计算后得到一个局部最优解为m＝587.2mm，γ0＝53.714 8°。优化前转向梯形臂长为568.0mm，优化后为587.2 mm，优化率为3.380%；优化前转向梯形底角为55.0000°，优化后为53.7148°，优化率为2.337%。

圆整参数后得到转向梯形臂长度为590mm，转向梯形底角54°。

优化后检修车内、外轮转角关系与阿克曼理论曲线对比如图5所示。

图5 转角关系实际与理论关系曲线对比

由图5可知，本文中所设计的梯形转向机构与阿克曼梯形机构的转向特性基本一致，误差很小，因此优化结果可以满足设计要求。

4 转向机构动力学仿真

4.1 三维模型建立

本文中的转向机构动力学仿真属于多体系统动力学问题，建立多体系统动力学方程时经常用到拉格朗日（Lagrange）乘子方法。根据本文所述的整体式梯形转向机构的特点，选择每个刚体质心的笛卡尔坐标和描述刚体方位的欧拉角作为系统的广义坐标，q＝［x，y，z，Ψ，β，φ］T。根据拉格朗日待定乘子可得系统动力学方程为［7］：

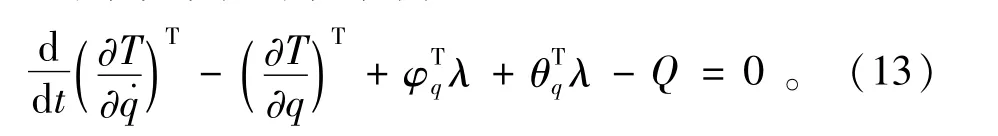
本文采用基于多体系统动力学理论的ADAMS作为动力学仿真分析软件。需要建立的零部件模型包括轮胎、轮架、转向梯形臂、转向横拉杆、转向传动装置、转向盘等，同时在ADAMS中完成复杂约束和力的添加，主要用到的元件包括连杆、圆柱、圆环、锥台等，用到的运动副包括旋转副、平动副、球副、等速副、齿轮副、刚性［8］。模型的创建步骤如下。

（1）建立转向机构三维模型。

（2）在车架与地面间创建固定副约束，使车架始终保持固定不动。

（3）分别在车轮与轮架、轮架与车架、转向横拉杆与轮架、转向传动轴与地面、转向盘与地面间创建转动副约束。

（4）在转向拉杆与轮架间创建球副。

（5）在转向传动杆间创建齿轮副以及等速副。

（6）在转向盘上添加电机，完成驱动副的创建。

按照以上步骤可以完成隧洞检修车转向机构的仿真模型：转向盘运动带动转向传动杆，传动杆通过齿轮副将运动传递给转向拉杆，拉杆拉动轮架，完成转向运动。

整体式梯形转向机构仿真模型如图6所示。ADAMS软件中模型的坐标方向为：沿转向机构横架方向为x方向，沿小车前进方向为y方向，垂直于地面的方向为z方向。

图6 检修车转向机构仿真模型

4.2 模型零件的相关参数

ADAMS模型中各个零件需给定其质量属性，才能执行静、动力学分析。质量属性用于确定在力的作用下引起模型的位置或速度发生变化时，机构的承受能力。机构的质量属性包括密度、体积、质量、重心和转动惯量。本文转向机构材料为Q235钢，密度按ρ＝1.2×7 850＝9 420（kg／m3）进行折算处理。在模型零件创建完毕后，其他质量属性参数将可以通过ADAMS软件自动计算得到。

动力学仿真过程中需要添加构件间的静态阻力系数以及动态阻力系数，分别添加0.3与0.1。另外检修车车轮属于金属材料，车轮与地面的动摩擦因数取0.5。

4.3 载荷计算

本文所做研究为对检修车转向机构的仿真分析，因此转向阻力矩是仿真的主要载荷，阻力矩以主动力的方式添加至轮胎。普通汽车加在轮胎上的转向阻力矩通过下式计算

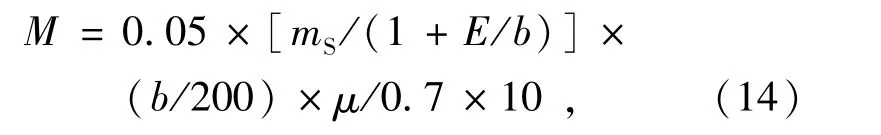
式中：M为转向轮所需总力矩，N·m；mS为前桥质量，kg；E为主销偏移量，mm；b为轮胎宽度，mm；μ为摩擦因数，重力加速度取10m／s2。

隧洞检修车共有水平与斜坡2种工况，各工况下相关参数取值如下。

（1）检修车水平运行工况相关参数：mS1＝3 000 kg，μ＝0.5，E＝0mm，b＝113mm。经计算，M1＝605 N·m。

（2）检修车斜坡运行工况相关参数：由于在斜坡工况下，检修车车身倾斜，重心前移，因此前桥载荷增大，mS2＝4 000 kg，其他参数与水平工况相同，经计算，M2＝807N·m。

但实际情况下，检修车车轮与地面接触线不水平，因此转向力矩的实际值应乘以修正参数，这个修正参数应为车轮母线与水平线夹角的余弦值，即2种工况下的实际转向阻力矩分别为

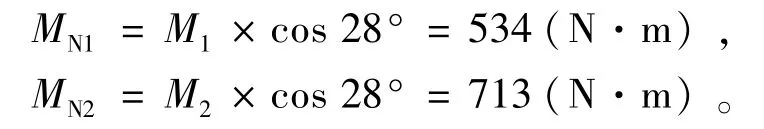
4.4 运动学及动力学仿真

完成模型建立与约束添加之后，就可以进入仿真阶段，而仿真阶段共分为以下4个步骤。

（1）添加接触力。由于隧洞内壁为弧形面，为使车轮与内壁贴合，车轮设计为锥台形状，啮合线近似为直线。由于车轮与路面接触部位始终为定长直线，即锥台母线，且车轮与路面摩擦系数为定值，因此车轮与路面的摩擦力大小为恒定值。但随着车轮转向，地面对车轮的摩擦力方向始终与车辆前进方向一致，因此可以得知地面对车轮的摩擦力大小不变，方向随时间变化。由于摩擦力大小不变，因此选择车辆转向时的2种典型工况进行分析，2种工况分别为水平行驶转向与坡道行驶转向。车辆简明受力分析如图7所示。

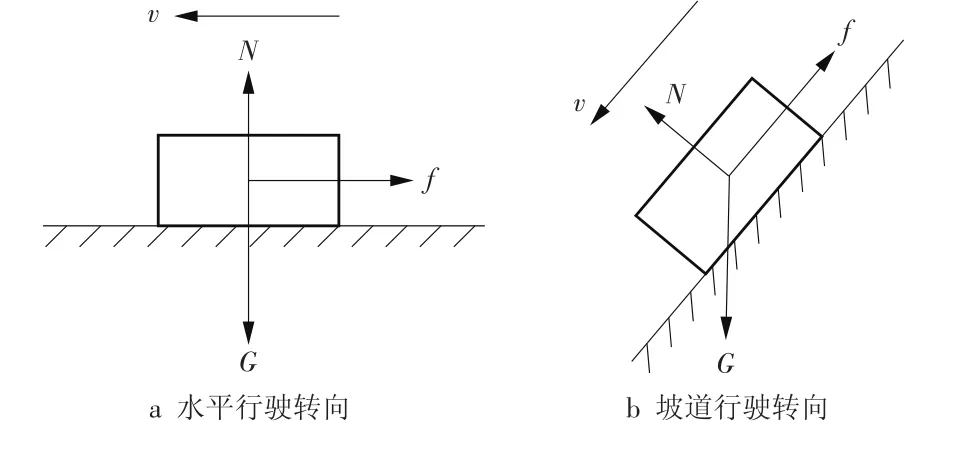
图7 车辆2种工况下受力情况

启动ADAMS／View，打开模型，选择Construction Geometry：Marker，在2个前轮底部分别创建Marker点；选择Applied Force：Torque（Single-Component）并设置Run-Time Direction选项为Body Fixed，将转向力矩添加到Marker点。分别在其余运动副处添加碰撞接触力，并在设置栏输入static coefficient为0.3，dynamic coefficient为0.1，stiction transition vel为10，fraction transition为10。

（2）添加驱动。选择Rotational JointMotion，在方向盘处的转动副上添加驱动，并设置step运动函数。

（3）验证模型。进行仿真前须进行模型的验证，只有验证了模型的构件数目、机构自由度、所加的各种约束的数目以及详细信息，模型才能进行正确仿真。

（4）进行仿真。选取仿真按钮Simulation，设置仿真时间为16 s，仿真步数为200步，点击Start后软件开始对转向机构进行动力学仿真。

4.5 仿真后处理

为保证转向机构仿真进行顺利，需首先对模型正确性进行检测。在ADAMS中进行模型检测非常简单，只需添加运动函数，双击Simulation，如能顺利完成，则模型无误。计算结果表明模型正确，参数选择合理。

完成检测之后，便可以在ADAMS／View模块中对其进行运动学及动力学仿真分析，然后通过ADAMS／PostProcessor模块进行后处理分析，在这一过程中可以分析整个仿真过程的数据变化，得到数据曲线，同时也可以将结果转化为动画形式，仿真结果清晰直观［9］。

根据车轮运动规律，仿真过程可分为4个阶段，分别为左转（0～5 s）、回正（5～10 s）、右转（10～13 s）、回正（13～16 s）。

4.5.1 内、外轮转角测量与分析

由于内、外轮转角关系直接影响到转向过程中车轮所受到的滑动摩擦大小，因此在运行工况中必须关注车轮转角的动态性能。车轮转向角度随时间变化规律如图8所示。从图8可以看出，所建模型的内转向轮最大转角为12°，外轮最大转角为10°。

图8 内、外轮转角随时间变化规律

在内、外轮转角关系之间建立测量，可以得到内、外轮转角关系仿真图，如图9所示。对比Matlab绘制的实际转角关系图可以看出，仿真结果与实际情况相符。

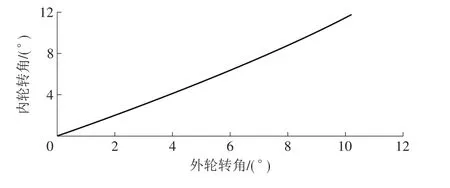
图9 内、外轮转角相互关系

4.5.2 转向盘力矩测量与计算

（1）水平工况。转向盘是驾驶员输入转向力矩的元件，转向盘上受到的力矩与驾驶员需要输入的力矩值相等。转向过程分为左转与右转2步，对应仿真时间段为1～10 s与10～16 s两部分。仿真结果如图10所示，由图10可以看出，在水平工况左转弯过程中方向盘绝大多数时间的力矩小于5000N·mm，已知方向盘半径为200mm，则双手的平均转向力小于25N，在第5 s时出现力矩突变，力矩剧增至186 kN·mm，所需转向力为930N；在水平工况右转弯过程中，方向盘绝大多数时间的力矩小于172 kN·mm，双手平均转向力低于860 N，在第13 s时出现力矩突变，力矩最大增至566 kN·mm，所需转向力为2830N。

（2）斜坡工况。同水平工况相同，转向过程分为左转与右转2步，对应仿真时间段分别为1～10 s与10～16 s。仿真结果如图11所示。由图11可以看出，斜坡左转弯过程中方向盘绝大多数时间的力矩小于8 kN·mm，则双手平均转向力小于40N，在第5 s时力矩剧增至391 kN·mm，所需转向力为1955N；在斜坡工况右转弯过程中，方向盘绝大多数力矩小于204 kN·mm，双手平均转向力小于1020N，在第13 s时出现了力矩突变，力矩最大增至611 kN·mm，所需转向力为3055N。

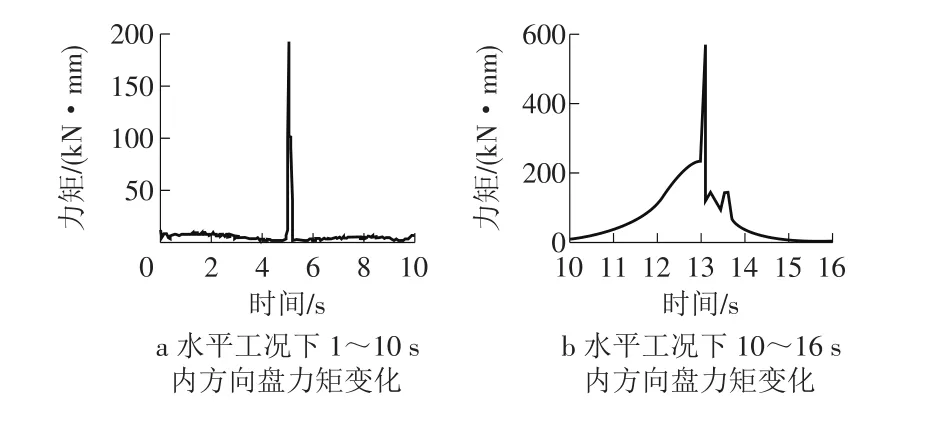
图10 水平工况方向盘力矩随时间变化规律

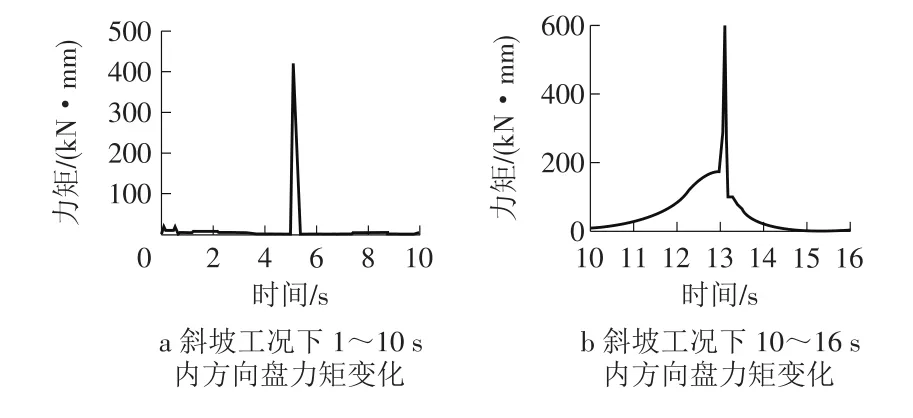
图11 斜坡工况方向盘力矩随时间变化规律

4.5.3 转向盘力矩分析［10］

由上文计算分析可知，在2种工况的转向过程中均出现了力矩突变，这些突变点称为奇异点，除奇异点及其附近点外，均称为非奇异点。针对奇异点与非奇异点分别分析，方向盘力矩随车轮转角变化情况如图12所示。

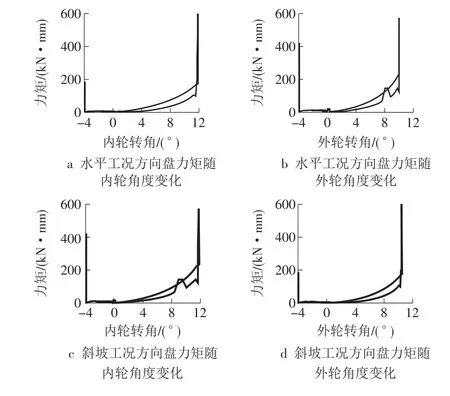
图12 方向盘力矩随车轮转角变化情况

（1）非奇异点。参照GB 17675—1999《汽车转向系基本要求》：“以10 km／h车速、24m转弯直径前行转弯时，不带助力时转向力应小于245 N”［11-14］，因为在2种工况右转向时，非奇异点转向盘转向力超过国家标准规定，转向时会产生转向沉重现象，甚至驾驶者无法提供足够的转向力，因此提出添加助力转向设备的建议。助力转向就是通过增加外力来抵抗转向阻力，让驾驶者只需更少的力就能够完成转向，最初是为了让一些自重较重的大型车辆能够更轻松的操作，但是现在已经非常普及，它让驾驶变得更加简单和轻松，并且让车辆反应更加敏捷，一定程度上提高了驾驶的安全性。目前转向助力设备的种类非常多，常用的助力设备有机械液压助力、电子液压助力及电动助力3种。

（2）奇异点。在奇异点及附近力矩突变处，转向力矩短时间内剧增。根据图12可知，在水平与斜坡2种工况下转向力矩值的奇异点均出现在两次车轮回正处。分析可知产生转向力矩突变的原因是变向时构件间产生刚性冲击，它会直接导致转向力不足，转向不成功。为解决这一问题，在实际应用中需要在传动件之间安装弹性阻尼器，一方面缓解刚性冲击，另一方面在弹性阻尼器的帮助下，转向系可自动回正，保持车辆稳定、直线行驶。

5 结束语

本文首先通过阿克曼原理，对该隧洞检修车梯形转向机构进行了初步设计，得到转向梯形底角、转向臂的初始参数，绘制检修车转向机构的理论转向特性曲线。然后利用Matlab中遗传算法的GA程序，对梯形转向机构的初始参数进行优化，优化结果与检修车理论转向特性曲线做分析比较，分析得到优化结果基本接近理论转向特性曲线，误差较小，可以作为设计参数。最后在ADAMS／View中对隧洞检修车梯形转向机构的三维模型进行动力学仿真分析，并得到数据图，最终得到以下结论。

（1）该转向机构所需提供的转向力过大，需添加转向助力设备。

（2）变向时各部件间容易产生刚性冲击，为缓解刚性冲击，并且使得转向机构带有一定的自动回正功能，因此建议在传动件之间增加弹性阻尼器。

［1］尚新民，王泰典，李佳翰，等.从检修案例探讨水工隧道全生命周期观点的设计考量［J］.隧道建设，2010，30（1）：211-210.

［2］陈集丰，段德高，杨荣.汽车转向梯形机构最佳参数确定［J］.西北工业大学学报，1995，13（4）：500-504.

［3］周全申，乔永钦，朱琳.车辆转向机构设计与分析［J］.河南工业大学学报，2006，27（2）：60-62，66.

［4］FELZIEN M L，CRONIN D L.Steering error optimization of the Macpherson strutautomotive front suspension［J］.Mechanism and Machine Theory，1985，20（1）：17-26.

［5］MLIIER G，REED R，WHEELER F.Optimum Ackerman for improved steering axle tire wear on trucks［J］.SAE，1991，103（3）：572-578.

［6］张德丰.MATLAB数值分析与应用［M］.北京：国防工业出版社，2009.

［7］洪嘉振.计算多体系统动力学［M］.北京：高等教育出版社，1999.

［8］李仲奎.基于虚拟样机技术的双前桥重型汽车转向系统仿真研究［D］.合肥：合肥工业大学，2006.

［9］熊光楞，郭斌，陈晓斌，等.协同仿真与虚拟样机技术［M］.北京：清华大学出版社，2004.

［10］GB 17675—1999汽车转向系基本要求［S］.

［11］王润琪，周永军，尹鹏.汽车前轮定位及回正力矩和转向力计算［J］.湖南科技大学学报，2010，25（1）：42-46.

［12］薄瑞峰，李瑞琴，刘昕明.轮式车辆转向机构的遗传算法优化设计［J］.中北大学学报：自然科学版，2009，30（2）：132-136.

［13］刘从华，赵斌，高秀华，等.多轴转向车辆转向机构优化设计［J］.农业工程学报，2007，2（9）：81-85.

（本文责编：弋洋）

U 463.4

B

1674-1951（2015）07-0018-06

胡友安（1963—），男，湖北黄陂人，教授，工学博士，从事工程力学、机械设计、水工金属结构等专业的教学和科研工作（E-mail：hya85191995＠qq.com）。

2014-06-03；

2015-06-15

周军（1978—），男，江苏盐城人，工程师，从事水工金属结构、液压启闭机设计方面的工作（E-mail：hizjun＠163.com）。

宋戈（1988—），男，陕西富县人，助理工程师，工学硕士，从事机械结构强度分析及优化设计方面的研究工作（E-mail：sglion851＠163.com）。