耦合超声振动系统的辐射特性

胡 静，王成会，李 锦

（陕西师范大学物理学与信息技术学院，陕西西安710119）

耦合超声振动系统的辐射特性

胡 静，王成会，李 锦

（陕西师范大学物理学与信息技术学院，陕西西安710119）

研究了一种用于液体中的由纵向夹心式换能器和纵径尺寸接近的金属圆柱辐射器构成的新型大功率超声振动系统。通过表观弹性法获得金属圆柱纵径耦合振动的机电等效电路及共振频率方程。对耦合振动系统的辐射特性进行了理论和数值分析，并通过实验进行验证。研究表明：该振动系统的圆柱辐射器的耦合振动可等效为一维径向振动和一维纵向振动的复合，其通过耦合系数相互作用；适当选择辐射圆柱的几何尺寸，振动系统产生强烈的纵径耦合振动，从而有效地辐射大功率超声波。

耦合；机电等效电路；共振频率

PACS：43.35.+d；43.38.+n

在功率超声和水声应用领域，常需要使用大功率的辐射器。纵向夹心换能器由于具有机械强度高，输出功率大，电声转换系数大以及结构简单等优点被广泛应用［1－5］。然而，随着如声化学、超声清洗以及超声液体处理等大功率超声技术的发展，对大功率超声换能器及具有大辐射表面的大功率辐射器的需求在增加。同时超声处理的液体容器的容积也在增大，需要具有多维辐射能力的超声波辐射器。在这种情况下采用传统的纵向夹心超声换能器存在两个方面的不足：纵向夹心式换能器的设计是基于一维设计理论，即换能器的横向尺寸要小于辐射声波波长的1／4，因此换能器的声波辐射面积受到限制，很大程度上限制了此类换能器辐射功率；另外，纵向夹心式超声换能器辐射能量基本上是沿着换能器的纵轴方向辐射，不能实现超声能量的空间辐射，使得在大容器超声液体处理中超声波作用范围受到了限制。

为了克服以上困难，本文将研究由传统的纵向夹心压电换能器和大尺寸金属圆柱复合而成的超声振动系统。其中大尺寸金属圆柱与传统的一维纵向辐射器（径向尺寸小于1／4波长）不同，该圆柱具有较大的径向尺寸，由于泊松效应将在径向和纵向产生复杂的耦合振动，从而提高辐射功率及超声作用范围。

本文对金属圆柱的耦合振动模态、位移分布和机电等效电路以及产生强烈耦合振动的条件进行分析，同时用数值方法研究辐射器的耦合振动。通过优化金属圆柱尺寸使其产生大功率和多维超声辐射，最后通过实验验证理论与数值分析的正确性。

1 大尺寸金属圆柱耦合振动分析

图1为大功率耦合超声振动系统的结构示意图，由传统的纵向夹心式换能器和纵径尺寸相当的金属圆柱构成，由于纵向夹心式换能器的横向尺寸远小于1／4波长，换能器的纵向振动是主要的，而当大尺寸金属圆柱被纵向夹心式换能器激励时，由于泊松效应金属圆柱将会产生复杂的耦合振动。图中H和R分别表示大尺寸金属圆柱的高和半径。

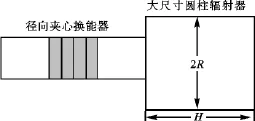
图1 大功率耦合超声振动系统结构示意图Fig.1 Geometrical diagram of a high power coupled ultrasonic vibrating system

1.1 金属圆柱耦合振动的机电等效电路

许多学者采用二阶近似理论、数值方法以及等效弹性等方法来研究各向同性的金属圆柱的耦合振动［610］。本文拟采用表观弹性法来研究大尺寸金属圆柱辐射体的耦合振动。根据表观弹性法，金属圆柱的耦合振动可简化为两个等价的一维振动：一维径向振动和一维纵振动，它们各自的等效弹性系数为

Er和Ez分别为径向等效弹性系数和纵向等效弹性系数，E和v分别是金属圆柱的杨氏模量和泊松比。定义弹性圆柱径向与纵向振动的机械耦合系数n＝－Tz／Tr，基于表观弹性法与一维振动理论，可得到耦合振动的纵向及径向机电等效电路，如图2及图3所示。

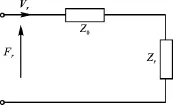
图2 耦合振动圆柱的径向振动等效电路Fig.2 Equivalent circuit of the radial vibration of the cylinder in coupled vibration

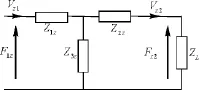
图3 耦合振动圆柱的纵向振动等效电路Fig.3 Equivalent circuit of the longitudinal vibration of the cylinder in coupled vibration

在图2中zr是圆柱的径向等效负载阻抗，Vr、Fr分别表示辐射金属圆柱外表面的径向振动速度和径向力，，其中Kr、Sr、Vr分别为等效径向波数、圆柱侧面积、以及径向振动速度，J0（KrR）和J1（krR）是贝塞尔函数。

图3中，ZL是圆柱输出端的等效纵向负载阻抗，Vz1、Fz1和Vz2、Fz2分别表示圆柱输入端与输出端的纵向振动速度和纵向力，Z1z＝Z2z＝jZz0tan（kzH／2），Z3z＝jZz0／sin（kzH／2），Zz0＝ρVzSz，Sz＝πR2，kz＝ω／Vz，Vz＝，其中Sz、kz、Vz分别为圆柱的截面积、波数和纵向振动速度。

根据机械耦合系数的定义，可得到如下关系

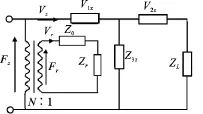
图4 圆柱耦合振动的机电等效电路Fig.4 Electro－mechanical equivalent circuit of the cylinder in coupled vibration

1.2 耦合振动的共振频率方程

从图4中可得到圆柱耦合振动的输入阻抗

其中纵向等效输入阻抗ZiL＝Z1z+，径向等效输入阻抗ZiR＝Zr+Z0，当输入阻抗等于零得耦合振动的共振频率方程：

在式（5）、（6）中等效负载阻抗ZiL和ZiR由几何参数、振动位移分布以及处理的负载媒介决定，在实际应用中很难确定。因此在设计振动系统中，通常忽略负载阻抗的作用，因此耦合振动的共振频率方程可简化为

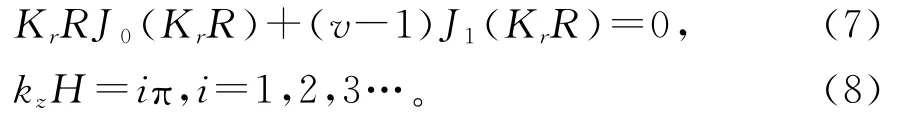
方程（7）和（8）中，共振频率和纵径耦合系数是未知的。因此，当材料参数和几何尺寸给定，圆柱的共振频率就能求出来，设方程（7）的根为M，也就是说kra＝M，结合方程（8）可得到以下方程：

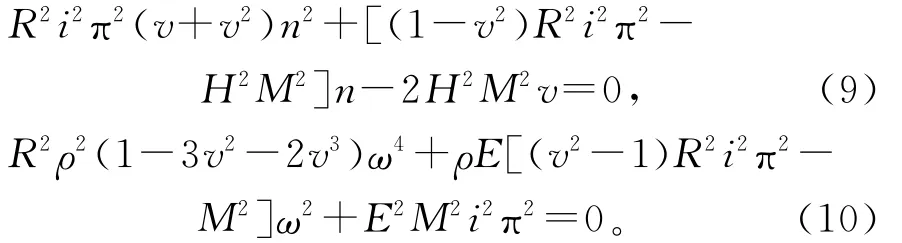
方程（9）和（10）是二次方程，存在两个解，基于表观弹性法，从方程（10）得到的两个共振频率分别为圆柱耦合振动的径向与纵向共振频率。

1.3 纵径尺寸对耦合振动的影响

当耦合振动的共振频率f＝20kHz时，由耦合振动频率方程（9）和方程（10），可得到几何尺寸间的相互关系以及几何尺寸对耦合程度的影响，如图5、图6所示。从图中可看出，当共振频率不变时，随着纵向尺寸的增大，径向尺寸逐渐减小而耦合系数n逐渐增大，说明当纵向尺寸逐渐增大时，圆柱逐渐趋于圆棒的振动，纵向应力逐渐增大，纵向振动增强。

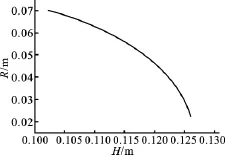
图5 圆柱纵径尺寸关系Fig.5 Analytical relationship between length－radius geometrical dimension

图6 圆柱尺寸与纵径耦合系数关系Fig.6 Analytical relationship between the coupling coefficient and the geometrical dimension of the cylinder

径向和纵向辐射阻抗在高频下可近似表示为

ρ和c为负载介质的密度和声速，将（12）、（13）式代入（11）式得

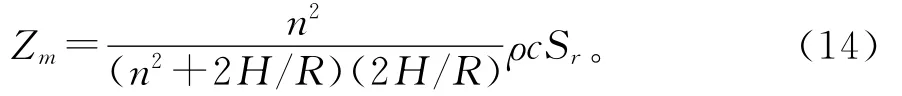
1.4 耦合振动的输入机械阻抗

在实际应用中，弹性圆柱体常作为超声辐射器，超声波辐射到周围的介质中，在这种情况下，负载阻抗不能被忽视。为简单起见，假设负载阻抗是电阻性的，即：ZL＝RL和Zr＝Rr，由图4可知，共振时圆柱的输入阻抗为

根据式（9）、式（14），可得圆柱的归一化输入阻抗与纵径尺寸比之间的关系，如图7所示，其中χ的归一化方式为χ＝Zm／（ρcSr）。

从图7中可看出，辐射圆柱的等效输入机械阻抗与几何尺寸有关，当纵向与径向尺寸比值接近临界值（H／R约为2）时，输入阻抗最大，此时，圆柱辐射器辐射出的声能也是最大。主要原因是：当圆柱几何尺寸接近临界值时，其纵向与径向的耦合最强，在径向和纵向都产生振动而辐射出声能。当几何尺寸远离临界值时，圆柱变为薄圆盘或细棒，在这种情况下，它主要在径向或纵向辐射超声能量。

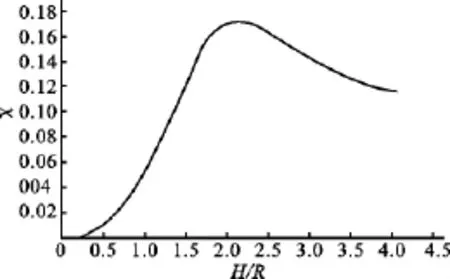
图7 归一化输入阻抗与圆柱纵径比关系Fig.7 Relationships between the normalized input mechanical impedance and the length－radius ratio of the cylinder

2 超声振动系统的数值仿真

有限元是分析耦合振动常用的分析方法，它能够分析复杂耦合振动系统的振动模态和共振频率。本文用有限元软件ANSYS来模拟仿真圆柱辐射体的耦合振动。图8是金属圆柱的振动模态变形图，图9和图10分别为圆柱辐射体在侧面和底面的振动位移分布，从仿真结果可看出，当纵径尺寸可比拟时，振动位移分布比较复杂，既有径向振动，也有纵向振动。

图8 金属圆柱的振动模态振型Fig.8 Coupled vibrational modal shape of the cylinder

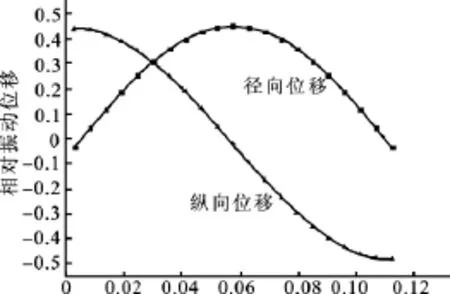
图9 圆柱侧面沿高度方向位移分布曲线Fig.9 Displacement distribution curve on the outer side surface of the cylinder

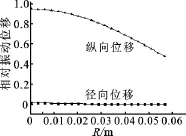
图10 圆柱底面沿半径方向位移分布Fig.10 Displacement distribution curve on the end surface of the cylinder

用ATILA仿真软件模拟仿真了振动系统圆柱辐射端在水中的声场分布，由于换能器振动系统是轴对称图形，为了计算简化，在“Problem Data”选项中，“CLASS”和“GEOMETRY”分别被设置成“2D”和“AXISYMMETRIC”，即在分析建模时，采用一半模型来建立二维模型。对换能器振动系统进行了谐响应分析，提取换能器振动系统在水中谐振时（共振频率为19 758Hz）的辐射声场分布。图11是振动系统圆柱辐射端在水中的辐射声场声压幅值，从图中可看出圆柱辐射端在径向和纵向都能辐射声波。

图11 超声振动系统辐射声压的幅值Fig.11 Magnitude of the radiated sound pressure for the ultrasonic vibrating system

3 复合振动系统的实验研究

实际应用中，大尺寸辐射圆柱往往通过夹心式纵振换能器激励，复合振动系统的大功率辐射性能由以下几个方面决定：首先，纵向夹心式换能器的共振频率应与辐射圆柱相同；其次，辐射圆柱应与纵向夹心式换能器牢牢地贴合在一起；第三，辐射圆柱应能产生强烈的纵向与径向振动。根据以上分析，设计了一个共振频率f＝20kHz的大功率硬铝圆柱，材料参数为：ρ＝2 700kg／m3，v＝0.34，C＝5 100 m／s；几何尺寸为：R＝56.3mm，H＝115mm。根据图12的实验装置测试了它的共振频率。ET和RT分别为共振频率高于圆柱辐射器共振频率的收发换能器，且几何尺寸很小，因此收发换能器对辐射体的影响可以忽略，改变正弦信号发生器的频率，当毫伏表的值达到最大时，信号频率就是圆柱的共振频率。测量值fm＝20 014Hz，ANSYS模拟值fn＝20 047Hz，理论值f＝20 000Hz，三者的结果一致。

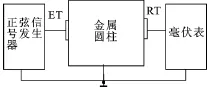
图12 圆柱共振频率测试实验装置原理图Fig.12 The experiment device diagram for the resonant frequency measurement of the cylinder

用螺栓将铝圆柱与大功率夹心换能器紧紧连在一起，如图13所示，对其振动性能进行测试。用激光测振仪测量了圆柱辐射体的振动位移分布，分别测量了圆柱侧面及底面的位移分布，如图14和图15所示，与图9和图10相比较，实验测量与数值仿真的位移分布一致。

图13 耦合振动系统的实物照片Fig.13 The photograph of the coupled vibrational system

图14 圆柱侧面径向位移的测量图Fig.14 Measured radial displacement on the outer side surface of the cylinder

图15 圆柱端面纵向位移的测量图Fig.15 Measured longitudinal displacement on the end surface of the cylinder

进一步观察了复合振动系统在大功率激励下的辐射性能。实验中，纵向夹心式换能器的输入电功率为300W，工作频率为换能器的共振频率，约为20kHz。图16是辐射体在水下辐射声波的照片。从照片中可看出，圆柱在水中产生剧烈的超声波辐射，在圆柱周围及底面形成大量气泡群，由此可看出圆柱在径向与纵向都能辐射超声波，与模拟仿真结果图11结果一致。

图16 耦合功率超声振动系统水中辐射声波的照片Fig.16 Photograph of power ultrasonic vibrational system radiate acoustic wave in water

4 结论

本文对应用于液体中的大功率超声波振动系统进行了研究。由表观弹性法得到了大尺寸辐射圆柱耦合振动的机电等效电路和频率方程，获得纵向与径向产生强烈耦合振动的条件，利用有限元数值模拟仿真了圆柱的耦合振动特性，并通过实验测量进行验证。综合分析，可得出以下结论：（1）金属圆柱的耦合振动可等效为两个一维振动，它们通过机械耦合系数相互作用；（2）圆柱耦合振动的机电等效电路由两条支路构成，一条支路等效为细棒纵向振动，另一条支路等效为薄圆盘的径向振动，两支路由决定耦合程度的机械转力换系数N来耦合；（3）圆柱耦合振动的等效输入机械阻抗的大小由几何尺寸决定，当圆柱纵向与横向尺寸比接近于1时，输入阻抗具有最大值，此时，圆柱在径向与纵向都能辐射出强烈的超声波；（4）通过适当选择圆柱的几何尺寸，大尺寸辐射圆柱能够有效地辐射大功率超声波。

此种振动系统可应用于功率超声，如超声液体处理、声化学、超声萃取等领域。

［1］林书玉.夹心式压电陶瓷功率超声换能器的优化设计［J］.压电与声光，2003，25（3）：199－202.

［2］Parrini L.New technology for the design of advanced ultrasonic transducers for high－power applications［J］.Ultrasonics，2003，41（4）：261－269.

［3］林书玉.鲜小军.功率超声换能振动系统的优化设计及其研究进展［J］.陕西师范大学学报：自然科学版，2014，42（6）：31－39.

［4］Dewulf J，Langenhove H V，Visscher A D，et al.Ultrasonic degradation of trichloroethylene and chlorobenzene at micromolar concentrations：Kinetics and modelling［J］.Ultrasonics Sonochemistry，2001，8（2）：143－150.

［5］Heikkola E，Miettinen K，Nieminen P.Multiobjective optimization of an ultrasonic transducer using NIMBUS［J］.Ultrasonics，2006，44（4）：368－380.

［6］Gazis D C，Mindlin R D.Extensional vibrations and waves in a circular disk and a semi－infinite plate［J］. Journal of Applied Mechanics，1960，27（3）：541－547.

［7］Gladwell G M L，Tahbildar U C.Finite element analysis of the axisymmetric vibrations of cylinders［J］.Journal of Sound and Vibration，1972，22（2）：143－157.

［8］Lin Shuyu.Analysis of the sandwich piezoelectric ultrasonic transducer in coupled vibration［J］.Journal of the Acoustical Society of America，2005，117（2）：653－661.

［9］周光平，梁召峰.纵径耦合振动管形振子的特性研究［J］.声学技术，2007，26（2）：320－325.

［10］Lin Shuyu.Coupled vibration of isotropic metal hollow cylinders with large geometrical dimensions［J］.Journal of Sound and Vibration，2007，305（1／2）：308－316.

〔责任编辑 李 博〕

The radiant properties of the coupled ultrasonic vibration system

HU Jing，WANG Chenghui，LI Jin
（School of Physics and Information Technology，Shaanxi Normal University，Xi'an 710119，Shaanxi，China）

A new kind of high power ultrasonic vibration system used in liquid is investigated. The vibration system is composed of a longitudinal sandwich transducer and a large metallic cylinder which has the equivalent size.Using the apparent elastic theory，the electro－mechanical equivalent circuit and frequency equations of the cylinder in radial－axial coupled vibration are obtained. The radiation characteristics of the coupling vibration system are analyzed and simulated，then they are verified in experiment.The results show that the coupled vibration of the cylinder can be equivalent to one－dimension radial and longitudinal vibrations which interact each other with coupling coefficient.As choosing the appropriate geometry size of the cylinder，the vibration system has a strong radial－axial coupled vibration，and the vibration system can effectively radiates high power ultrasound.

coupling；electro－mechanical equivalent circuit；resonant frequency

O426.2

：A

1672－4291（2015）06－0030－06

10.15983／j.cnki.jsnu.2015.06.262

2014－11－08

国家自然科学基金（11474192，11474191）；陕西省自然科学基金（2013JQ1017）

胡静，女，讲师，博士，研究方向为超声工程。E－mail：hjwlx＠snnu.edu.cn