Midas/Civil在大跨斜拉桥几何非线性分析中的应用
赵 晓 婷
(东北林业大学,黑龙江 哈尔滨 150040)
Midas/Civil在大跨斜拉桥几何非线性分析中的应用
赵 晓 婷
(东北林业大学,黑龙江 哈尔滨 150040)
结合某大跨径混合梁斜拉桥工程,运用Midas/Civil软件建立了其完整有限元模型,阐述了斜拉桥各部件具体简化方法以及斜拉桥合理成桥状态计算方法,对各种典型工况实现方法进行了说明,通过比较线性计算结果与非线性计算结果,论述了该软件在大跨度桥梁几何非线性分析时的应用方法。
Midas/Civil,大跨径斜拉桥,几何非线性分析
0 引言
计算机仿真分析技术能及时、科学地指导施工,现已逐步应用于大跨度斜拉桥的施工中。大跨度斜拉桥是一种轻柔的结构形式,作用力与变形量之间不是线性关系,荷载增减效应不能简单叠加,误差逐渐累积从而影响桥梁稳定性。因此,几何非线性分析尤为重要。斜拉桥几何非线性效应主要包括三个方面:拉索垂度效应、主梁与桥塔的梁柱效应及大位移效应。本文结合一座大跨径混合梁斜拉桥,对Midas/Civil软件在该类桥梁的几何非线性分析的应用进行介绍,并对一些需要注意的问题进行探讨。
1 工程实例概况
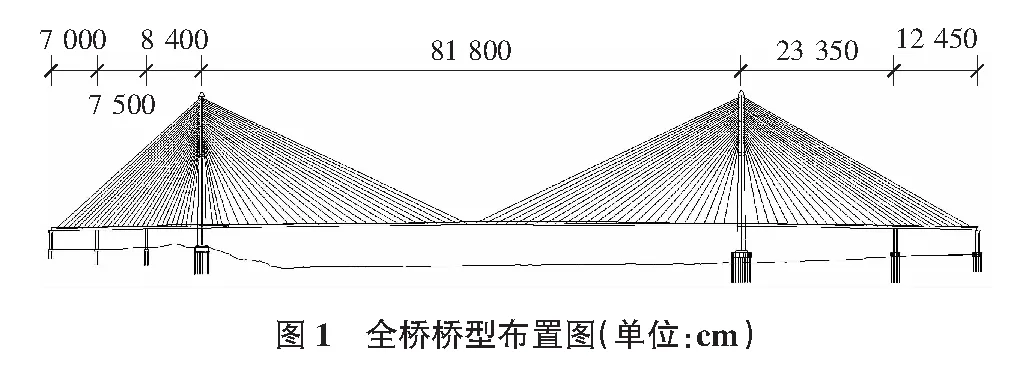
该算例上部结构是双塔不对称混合梁斜拉桥,跨径组成为(70+75+84)m+818 m+(233.5+124.5)m。左边跨设有一个交界墩和两个辅助墩,边中跨比为0.280;右边跨设有一个交界墩和一个辅助墩,边中跨比为0.438(见图1)。主桥桥面布置为双向六车道,桥面去除风嘴和布索区其宽度为33.5 m,索面间距为35.5 m;左边跨全跨至中跨距索塔32.5 m处主梁采用预应力混凝土箱梁,索距为7.5 m;其余部分采用钢箱梁,索距为15 m,右边跨尾索区索距为10.5 m;拉索在左塔内壁上间距为2.6 m~4.4 m,由28对斜拉索组成;右塔内壁上间距为2.5 m~4.2 m,由26对斜拉索组成,全桥共54对斜拉索。
2 计算模型与分析
2.1 各部件简化情况
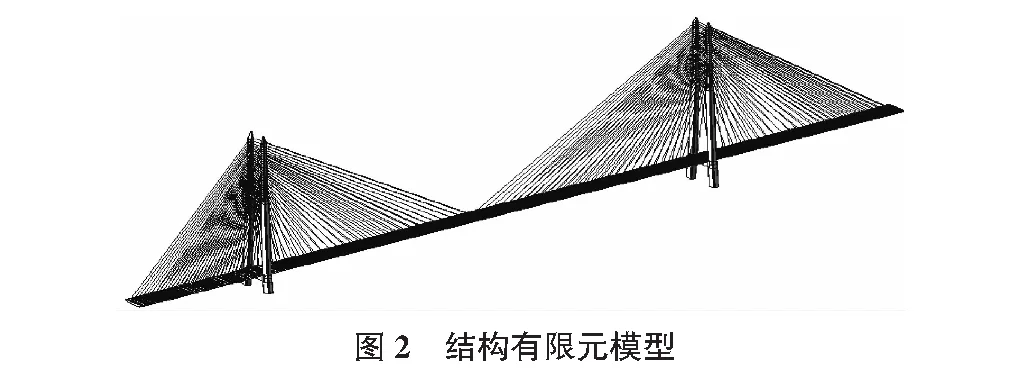
模型采用空间杆系有限元,划分单元应结合施工阶段且遵循一般的有限元划分单元规则。全桥共有679个单元,主梁单元是1~301,斜拉索单元是1 000~1 215,左塔单元是2 000~2 081,右塔单元为3 000~3 079。渲染后的桥梁模型如图2所示。
1)索塔。
索塔高度很大而横断面相对较小,承受荷载很大,因此建模时采用实际的横断面尺寸来模拟桥塔。索塔塔柱采用的是普通混凝土或预应力混凝土结构,若分别将混凝土和钢筋实际模拟,会使得模型极度复杂且模型分析时耗费大量的时间,因此本文采用将混凝土和钢筋当作一种材料模拟的方法,适当改变其自重系数和弹性模量。
2)主梁。
本文采用单主梁模型中的“鱼骨刺”来模拟,并将横隔梁简化为刚度极大、质量为零的刚性连接模拟。鱼骨刺形模型的特点是将主梁的刚度、质量都集中在主梁节点上,且主梁节点和斜拉索的主梁锚点通过钢臂连接。因为本工程中的主梁是扭转刚度比较大的闭口截面主梁,故鱼骨刺模型较为适用。
3)桥塔与斜拉索连接处。
该算例的斜拉索固定在钢锚箱外边缘上,故应采用钢臂将索塔中心线与索端连接起来。本文用刚度极大、质量为零的刚性连接模拟,不仅实现了斜拉索的实际锚固位置,还实现了模型的简化。
4)边界条件。
该算例采用半漂浮结构体系,分别在索塔下横梁上和辅助墩处布置双向活动支座,在过渡墩处布置纵向滑动支座并限制其横向运动,梁侧布置横向抗风支座。建模采用的具体约束形式如表1所示。
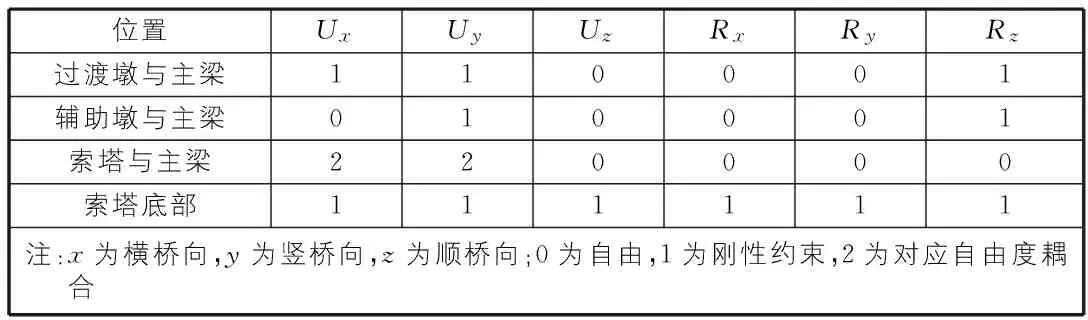
表1 有限元模型的边界条件
2.2 Midas/Civil分析斜拉桥几何非线性方法
1)合理成桥状态。该算例采用零位移法对斜拉索进行索力优化,配合Midas/Civil的未知荷载系数功能,求得一个合理成桥状态。具体步骤如下:
完成成桥阶段模型→给各索赋予单位初张力→建立荷载组合(包括恒荷载和单位荷载)→进行结构分析→求未知荷载系数(设置控制条件,必要时利用影响矩阵调整未知荷载系数,并且将其反映到荷载组合中)→确认荷载组合结果。
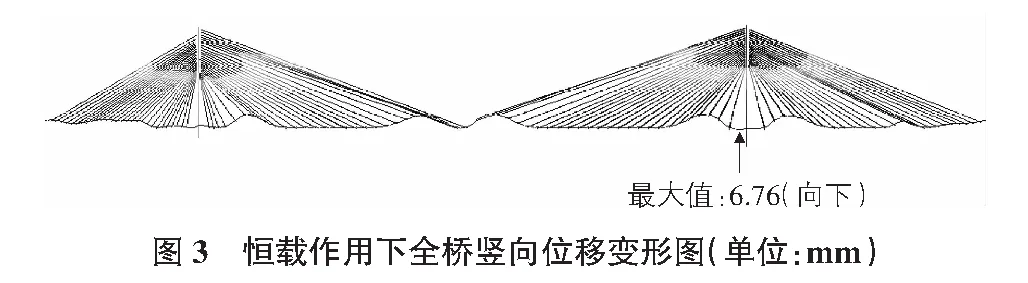
该算例在计算时,对混凝土单元施加重力加速度10 N/kg;设置钢箱梁单元容重为0,并且施加等效于自重的梁单元荷载;依照图纸施加相应的二期荷载和二期压重;依照图纸施加预应力荷载;施加相关约束,此后进行静力求解。进入后处理查看成桥阶段竖向位移如图3所示。
2)几何非线性计算工况及实现方法。采用Midas/Civil软件分析各个几何非线性因素对结构产生的定量影响,本文建议以下计算工况:
工况1:线性计算。即不考虑任何一种非线性因素。在软件中,采用桁架单元模拟斜拉索,对模型进行线性分析即可实现。
工况2:斜拉索垂度效应分析。将斜拉索的弹性模量用Ernst公式修正,不考虑大位移效应及梁柱效应。在软件中,采用索单元模拟斜拉索,对模型进行线性分析即可实现。
工况3:结构大位移效应分析。未考虑斜拉索垂度效应和梁柱效应。在软件中,采用桁架单元模拟斜拉索,然后设置几何非线性分析控制,就可以实现。
工况4:桥塔梁柱效应分析。在成桥模型中,只设置“P—Δ控制”就可以实现。
工况5:综合考虑斜拉索垂度效应和大位移效应。把斜拉索设置成索单元,然后设置几何非线性分析控制就能实现。
需要注意的是,主梁与梁塔的梁柱效应影响分析即P—Δ,只适用于小变形情况,对于大变形情况,单考虑P—Δ分析,误差很大。对于大位移情况,梁柱效应是通过引用几何刚度矩阵或者稳定函数来体现。所以进行大位移分析,则不需要考虑P—Δ分析。Midas中,这两者不能进行同时分析。
本文选取中跨合龙的施工阶段,对比工况5的几何非线性结果与线性计算结果,以主梁位置为横坐标,左侧混凝土梁端为x坐标原点,竖向位移为纵坐标。因左边跨与右边跨结果不明显,故选取跨中的竖向位移结果,如图4所示。
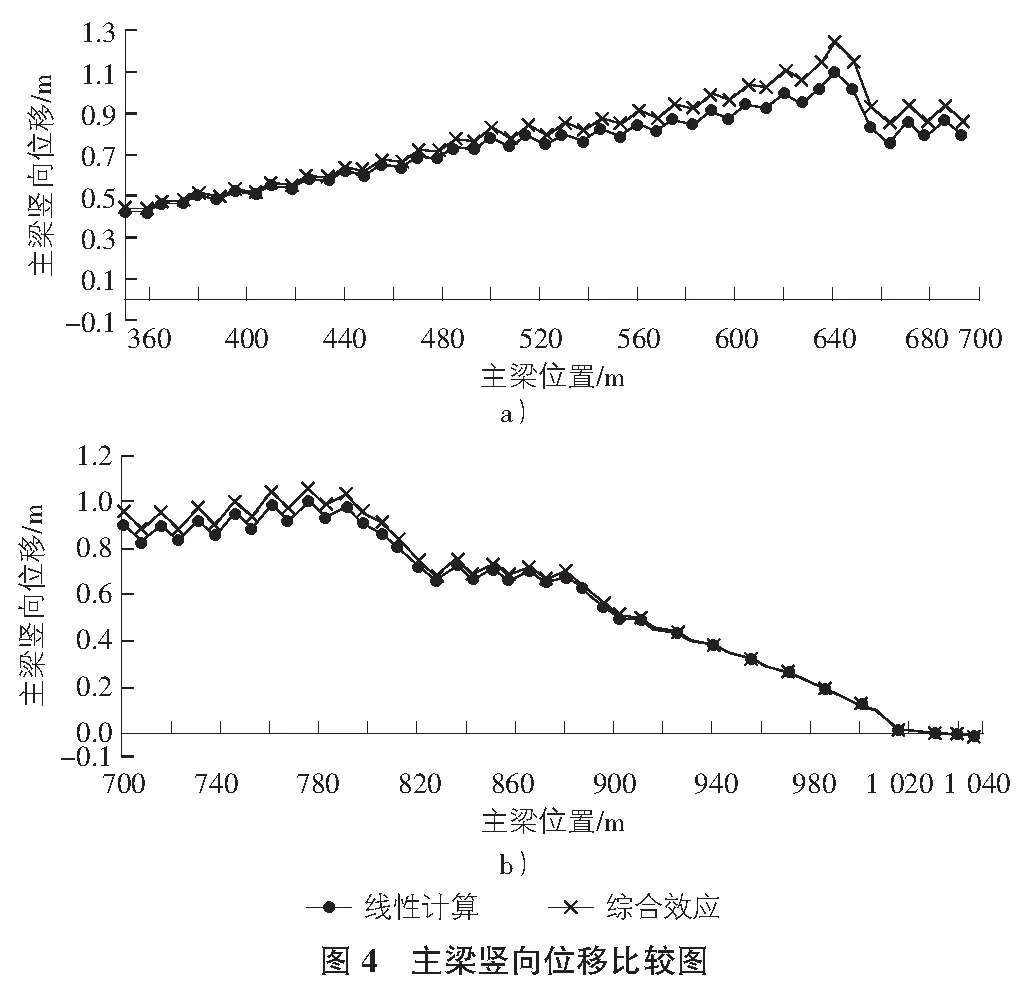
由图4可知,在中跨合龙的施工阶段里,斜拉索垂度效应和大位移效应的综合作用使得竖向位移最大由1.099 m变化到1.251 m,增大了13.9%。由此可见,大跨径斜拉桥几何非线性影响不可忽视。
3 结语
有限元分析软件Midas/Civil能够实现大跨度斜拉桥各种几何非线性因素的定量分析。本文结合一座大跨度混合梁斜拉桥工程示例,介绍斜拉桥合理成桥状态计算方法、斜拉桥各部件简化方法,以及各种工况实现方法,可以供类似工程参考。
[1] 陈铁冰.大跨度斜拉桥几何非线性有限元分析[J].交通科技与经济,2009(4):37-38,41.
[2] 胡 娟.Midas/Civil软件在大跨径桥梁悬臂施工中的应用[J].西部交通科技,2011(10):61-64.
[3] MIDAS.土木结构分析手册[M].北京:北京迈达斯技术有限公司,2005.
The application of Midas/Civil in large span cable stayed bridge geometric nonlinear analysis
Zhao Xiaoting
(LargeNortheastForestryUniversity,Harbin150040,China)
Combining with a large span hybrid girder cable stayed bridge engineering, this paper established its complete finite element model using Midas/Civil, elaborated the specific simplified method of cable stayed bridge each component and reasonable bridge situation calculation method of cable stayed bridge, illustrated the implementation method of various typical working conditions, through comparing the linear calculation results and nonlinear calculation results, discussed the application method of this software in large span bridge geometric nonlinear analysis.
Midas/Civil, large span cable stayed bridge, geometric nonlinear analysis
2015-06-05
赵晓婷(1991- ),女,在读硕士
1009-6825(2015)23-0153-02
U448.27
A

