考虑磁致伸缩效应永磁电机的振动噪声研究
韩雪岩,张哲,吴胜男,陈健
(沈阳工业大学国家稀土永磁电机工程技术研究中心,辽宁沈阳110870)
考虑磁致伸缩效应永磁电机的振动噪声研究
韩雪岩,张哲,吴胜男,陈健
(沈阳工业大学国家稀土永磁电机工程技术研究中心,辽宁沈阳110870)
硅钢片的磁致伸缩是永磁电机产生振动噪声的原因之一。本文基于压磁方程,建立了考虑磁致伸缩效应的磁-机械耦合模型,给出求解区域内的基本假设及相应的边界条件,以一台11kW永磁同步电机为例,应用有限元计算了在理想电流和实验电流供电下由电磁力和磁致伸缩效应两种振动源单独和共同作用时引起的振动;在此基础上分析了电机周围的声场分布。为了验证模型,对该永磁电机的振动和噪声分别进行了实验研究。理论计算与测量结果的比较验证了该耦合模型的正确性,为在设计阶段计算永磁电机振动噪声大小、分布和寻求新的降噪措施,提供了理论依据和计算方法。
永磁电机;磁致伸缩;磁-机械耦合;有限元分析;振动噪声
1 引言
通常对电机振动噪声的数值计算只考虑电磁力对电机的影响,不考虑磁致伸缩效应。但是电机中,定子铁心由硅钢片叠压而成,铁心由于硅钢片的磁致伸缩会引起内部发生变形和应力,使定子铁心随励磁频率的变化作周期性振动,当磁致伸缩频率与铁心固有频率发生共振时,会对电机的振动噪声有一定的影响。因此考虑磁致伸缩效应的电机振动噪声研究是必要的。
目前,国内外对磁致伸缩效应的研究成果主要应用在超磁致伸缩换能器和传感器上[1,2]。河北工业大学王博文教授根据压磁效应(磁致伸缩逆效应),建立了超磁致伸缩换能器的磁弹性动态模型,在不同工作情况下,对换能器系统进行模型的仿真计算并与实验结果对比。磁致伸缩效应对电机振动噪声影响的研究正处于起步阶段[3-6]。2000年,比利时Koen Delaere等对磁致伸缩导致电气装置的振动噪声进行了研究,利用磁力耦合有限元方法获得磁致伸缩材料特性。研究表明,电磁力和磁致伸缩力通常共同作用改变磁性材料的形状,磁致伸缩力导致材料变形或振动[7]。2006年英国帝国理工大学博士Anouar Belahcen基于虚功原理结合有限元方法建立磁弹性耦合方程,推导了磁致伸缩力与磁场的关系[8]。2008年波兰Jerzy Podhajecki等学者通过基于有限元算法的二维数值程序的编写,对无刷直流电机空载时由麦克斯韦力和磁致伸缩引起的振动进行了计算。通过以上计算分析,最后得到以下结论:定子铁心中的磁致伸缩会使电机振动的量级增加;磁致伸缩引起的电机振动约等于麦克斯韦力产生的振动的20%[9]。2011年韩国首尔国立大学Pan Seok Shin和韩国国民大学Hee Jun Cheung,基于虚功原理结合磁弹性有限元方法推导了关于形变和磁场的关系,对3kW的无刷直流电机的磁致伸缩力和振动模态进行了模拟计算[10]。综上所述,由磁致伸缩效应引起的电机振动特性国外已有少量研究,而国内在这方面的研究还鲜有报道。
为此,本文建立了考虑铁心磁致伸缩特性的电磁-机械耦合数值模型和声场计算数学模型。以11kW的永磁电机为例,运用有限元法对该电机磁场分布、电机的定子系统形变、电机周围声场分布进行了计算,分析了在理想电流和实验电流供电下由电磁力和磁致伸缩效应两种振动源单独和共同作用时引起的电机振动和噪声。通过样机试验与计算结果的对比,验证了模型和计算方法的正确性。该分析方法可在设计阶段给出铁心磁场、振动的大小分布的数值,并为永磁电机振动噪声控制提供参考依据。
2 永磁电机振动的磁-机械耦合数学模型
本文选用多物理场耦合分析软件COMSOL Multiphysics,建立了磁-机械耦合模型,对永磁电机的振动进行仿真研究。
电磁分析时选用AC/DC模块中的旋转机械-磁模块,求解域中的方程为:
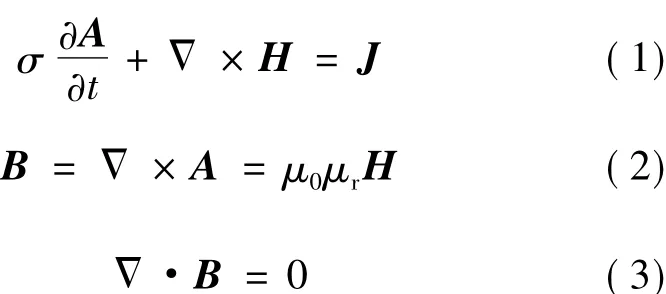
式中,σ为电导率;A为磁矢位;μ0为真空磁导率;μr为相对磁导率;J为外部电流密度;B为磁通密度;H为磁场强度。
结构场分析选用结构力学模块中的固体力学模块,求解域中的方程为:

式中,ρ为密度;u为位移矢量;F为载荷;v为泊松比;T为应力;Ti为初始应力;C为刚度矩阵;S为应变;Si为初始应变。
磁致伸缩数学模型通常用线性压磁方程来描述,它包括两个公式:其一,应变的方程,即外加应力引起的材料弹性应变和外加磁场引起的磁应变之和;其二,磁感应强度的方程,即外加应力引起的磁感应强度和外加磁场引起的磁感应强度之和。当只考虑材料在单一轴向的伸缩时,线性压磁方程表示为:

式中,ε为应变;ηH为杨氏模量的倒数;d为压磁应变系数;H为磁场强度;uT为在恒定压力下的磁导率。
本文讨论的磁致伸缩效应不包含外加应力的作用,因此式(6)和式(7)可简化为:

在计算电机的机械振动时,选用COMSOL Multiphysics中的固体力学模块,定子与机壳接触处的边界设为连续,将电机与地面的接触部分设为固定约束。将定子受到的电磁力根据式(10)添加到定子齿部表面。
单位面积径向电磁力的瞬时值可以表示为:

式中,B(t)为电机气隙磁密;μ0为真空磁导率。
整个耦合过程建立的磁机械耦合方程为:

式中,S为电磁刚度矩阵;K为机械刚度矩阵;A和u表示要求解的磁场矢量和振动位移矩阵;J为外部电流密度;F为作用力。
通过间接耦合的方式,使用旋转机械-磁模块计算得到定子磁密分布,然后调用磁致伸缩单值曲线,得到定子铁心的形变,其与电磁力产生的形变进行叠加,即可在计算电机振动时考虑磁致伸缩效应。
3 电工硅钢片磁致伸缩特性的测量
研究磁致伸缩效应对电机振动噪声的影响离不开磁致伸缩特性的测量实验。为此,本文按照2010年国际电工委员会公布的硅钢片的磁致伸缩特性测量IEC标准[11]对电机铁心使用的无取向硅钢片进行了测量。
本文将DW270的无取向硅钢片裁制成100mm ×500mm大小,应用辽宁省现代电工装备理论实验室的一维磁致伸缩测量系统对该样片进行了测试。得到不同磁通密度幅值(0.1~1.7T,间隔0.1T)下的磁致伸缩回环,也称为蝴蝶曲线,其中1.2T和1.7T测得的蝴蝶曲线如图1(a)所示。为了将测量的磁致伸缩数据应用于电机铁心的形变仿真计算,本文利用磁通密度幅值与磁致伸缩峰峰值的关系数据,将磁致伸缩回环处理为磁致伸缩单值曲线,进一步通过三次样条插值得到平滑的磁致伸缩单值曲线,如图1(b)所示。
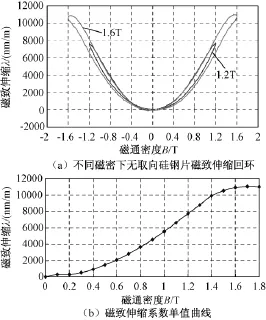
图1 永磁同步电机铁心硅钢磁性测量Fig.1 Magnetic propertiesmeasurement of silicon steel of PMSM core
4 数值计算与实验对比分析
本文以一台11kW的永磁电机为例,基于以上的数学模型和测量数据,进行了数值计算和实验比较,电机主要参数如表1所示。

表1 电机主要参数Tab.1 Main parameters ofmotor
4.1 正弦波供电永磁电机振动的数值计算与实验
4.1.1 理想正弦波供电下永磁电机振动计算
由于在实际情况下硅钢片并非处于自由状态,为了使建立的模型更接近实际,本文建立了机壳上有散热筋的二维电机模型。
建立模型后,通过多物理场耦合分析软件COMSOL Multiphysics的前处理功能将模型分为旋转部分、定子和机壳三部分,产生两个边界。
在计算电磁场时选用COMSOL Multiphysics中AC/DC模块中的旋转机械-磁模块,旋转部分和定子接触处的边界设为连续,选用电路模块对绕组添加正弦波空载电流。
在计算电机的机械振动时,选用COMSOL Multiphysics中的固体力学模块,定子与机壳接触处的边界设为连续,即两者紧密连接。通过间接耦合的方式,使用旋转机械-磁模块计算得到定子磁密分布,调用磁致伸缩单值曲线得到形变,将这个形变设为初始应变,即可在固体力学模块计算时考虑磁致伸缩效应。本文电机振动计算时只考虑定子,未考虑转子影响。
为了研究磁致伸缩效应对电机振动的影响,本文计算了电磁力单独作用、磁致伸缩效应单独作用、两种振动源共同作用时电机定子系统的形变。
当电机工作在空载状态下额定频率时,为了便于比较,选择不同时刻(0.04s、0.08s、0.12s、0.16s)进行计算,电磁力和磁致伸缩共同作用引起的定子铁心和机壳变形如图2所示。

图2 不同时刻电磁力和磁致伸缩共同作用引起的瞬态形变(理想正弦波)Fig.2 Transient deformations with MSand electromagnetic force at different time(ideal sine wave)
通过计算发现铁心磁致伸缩效应对定子振动变形有一定的影响,电磁力引起的铁心形变比磁致伸缩引起的铁心形变约大一个数量级。
本文还计算了电机工作在额定频率时,定子上点1(如图2所示)在两个方向上的振动加速度(4周期),如图3所示。其中,图3(a)是在横向上三种情况下的计算结果,图3(b)是纵向的加速度,图3 (c)是合成加速度曲线。从图3中的这些数据可以很容易地看到,磁致伸缩对电机的振动有很大的影响,使电机的振动加速度明显变大。

图3 点1的振动加速度(理想正弦波)Fig.3 Accelerations of particle on stator(ideal sine wave)
4.1.2 实验正弦波供电下永磁电机振动计算
为了使仿真更接近实际,本文使用11kW永磁电机实测得到的空载电流波形进行数值计算,电流波形如图4所示。计算时以内插的形式调用电流波形,其他计算过程与理想正弦波计算基本相同,得到不同时刻下三种状态引起的瞬态定子铁心和机壳形变,其中电磁力和磁致伸缩共同作用引起的定子铁心和机壳变形如图5所示。
通过计算结果发现电磁力引起的铁心形变比磁致伸缩引起的铁心形变约大一个数量级,变化规律和理想正弦波供电下基本一致。

图4 实验测得的空载电流波形Fig.4 Measured no-load current curves

图5 不同时刻电磁力和磁致伸缩共同作用引起的瞬态形变(实验正弦波)Fig.5 Transient deformations with MSand electromagnetic force at different time(experimental sine wave)
通过计算得到电机工作在额定频率时,机壳上点1在三种状态下求得的振动加速度(4周期),如图6所示。可以看出,磁致伸缩对电机振动有明显的影响,使电机的振动加速度明显变大。
为了研究磁致伸缩与电磁力对电机振动的贡献,对以上两种情况下电磁力单独作用、磁致伸缩单独作用、两者共同作用的计算结果进行对比分析,结果见表2,表中比值为共同作用时计算结果与单独作用时的比值。
由表2可以看出,在两种电流源下引起的振动位移、振动速度的变化规律基本一致。由于实验正弦波的畸变率较大,引起的电机振动比理想正弦波引起的振动明显增大。虽然磁致伸缩在不同时刻会增强或削弱电机的振动,但是从整体上看磁致伸缩使电机的振动位移、振动速度和振动加速度增大。

表2 两种电流源引起的电机振动对比Tab.2 Vibration in motor caused by two kinds of current source

图6 点1的振动加速度(实验正弦波)Fig.6 Accelerations of particle on stator (experimental sine wave)
4.1.3 正弦波供电下永磁电机振动的测量
永磁同步电机振动测量系统由加速度传感器、数据采集系统和样机组成,如图7所示。通过此系统测量空载运行时11kW永磁同步电机产生的振动加速度。

图7 永磁同步电机振动测量系统Fig.7 Testing system for PMSM vibrationmeasurement
由于之前计算的振动点在散热筋上,而实际电机散热筋较窄无法用传感器测量,因而实验测量点选择在与铭牌对称的位置上。实验和计算结果汇总见表3。

表3 正弦波电流供电下计算结果与实验测量结果Tab.3 Calculated results using sine wave current and results of experimentalmeasurements
通过表3计算和测量值的比较说明,实验电流下计算值与理想电流下计算值相比更接近实验值,且实验值比计算值略大。由于实验时已将电机风扇拆除,因此造成这种情况主要原因是:模型是二维的,并未考虑整机的装配;电机振动计算只考虑定子,未考虑转子动平衡的影响。
4.2 正弦波供电永磁电机噪声的数值计算与实验
在计算永磁电机的噪声时,选用COMSOL Multiphysics压力声学模块,对电机的声场进行了分析。
其中,选择声场辐射方式为平面波辐射。将电机机壳与空气接触边界作为振动的源,添加到法向加速度项中,通过调用固体力学模块中求得的加速度结果即可求出电机周围声压级分布。
为了对比分析计算和实验结果,本文计算了某时刻(t=0.03s)理想正弦波供电和实验正弦波供电下电机的周围声压级分布,其中实验正弦波供电下两种振动源共同作用时的计算结果如图8所示。
永磁电机的噪声实验在沈阳工业大学国家稀土永磁电机工程技术研究中心消声室内进行。永磁同步电机噪声测量系统由噪声分析仪、数据采集系统和样机组成,如图9所示。通过此系统测量空载运行时11kW永磁同步电机产生的噪声。
测量点的位置如图8所示。各点噪声分析和测量结果记录见表4。
通过表4中各点的计算值和测量值的比较说明,考虑磁致伸缩效应的计算结果误差更小,实验电流计算值更接近测量值。由此可见,考虑磁致伸缩效应对永磁电机振动噪声的分析值与实际噪声的大小基本相等,误差范围能够满足工程设计的要求,对设计阶段分析电机噪声大小和分布具有重要的指导意义。
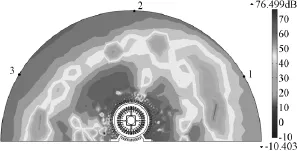
图8 实验电流供电下电机的周围声压级分布Fig.8 Sound pressure level around motor under experimental current

图9 永磁同步电机噪声测量Fig.9 Testing system for PMSM noisemeasurement

表4 噪声分析和测量结果Tab.4 Results of analysis and measurement of noise
5 结论
本文对永磁同步电机进行了电磁-机械振动的二维有限元数值计算,分析了电机周围振动噪声的分布,并进行了相关实验研究,得出以下结论:
(1)考虑硅钢片磁致伸缩效应,建立了永磁电机二维电磁-机械耦合数值模型。
(2)采用该耦合模型对永磁电机进行了磁场和振动的数值分析,计算结果与实验结果比较吻合,验证了该数值模型的正确性。计算结果表明,磁致伸缩对电机的振动产生重要贡献,在设计电机铁心时应考虑铁心的磁致伸缩效应。
(3)在基于耦合模型振动计算的基础上对电机周围振动声场进行了分析,分析值与测量值相符,证实了该分析方法的可靠性。该方法对设计阶段分析电机噪声大小和分布具有重要的指导意义,并为降低电机噪声提供理论分析方法和依据。
[1]Yasukazu Sato,Keita Shinohara.Power-saving drive in 2-position control of giant-magnetostrictive actuator[J].IEEE Transactions on Magnetics,2009,45(10):4554-4557.
[2]F T Calkins,R C Smith,A B Flatau.Energy-based hysteresismodel for magnetostrictive transducers[J].IEEE Transactions on Magnetics,2000,36(2):429-439.
[3]Rongge Yan,Bowen Wang,Qingxin Yang,et al.A numerical model of displacement for giant magnetostrictive actuator[J].IEEE Transactions on Applied Super-couductivity,2004,14(2):1914-1917.
[4]翁玲,王博文,李淑英,等(Weng Ling,Wang Bowen,Li Shuying,et al.).磁场和应力作用下的超磁致伸缩换能器的动态模型(Dynamic model of giantmagnetostrictive transducer under magnetic field and stress)[J].电工技术学报(Transactions of China Electrotechnical Society),2008,23(12):17-22.
[5]张纳,王博文,李淑英,等(Zhang Na,Wang Bowen,Li Shuying,et al.).磁致伸缩、压电层状复合磁电传感器非线性动态有限元模型(Nonlinear dynamic finite elementmodel formagnetostrictive/piezoelectric laminated compositemagnetoelectric sensors)[J].电工技术学报(Transactions of China Electrotechnical Society),2012,27(7):146-152.
[6]孙英,王博文,翁玲,等(Sun Ying,Wang Bowen,Weng Ling,et al.).磁致伸缩致动器的输出位移与输入电流频率关系实验研究(Study of the relationship between output displacement and input current frequency for magnetostrictive actuator)[J].电工技术学报(Transactions of China Electrotechnical Society),2008,23 (3):8-13.
[7]Koen Delaere,Ward Heylen,Ronnie Belmans,etal.Finite element analysis of electrical machine vibrations caused by Lorentz,Maxwell and magnetostriction forces[A].IEE Seminar on Current Trends in the Use of Finite Elements(FE)in Electromechanical Design and Analysis[C].London,UK,2000.9/1-9/4.
[8]Anouar Belahcen.Vibrations of rotating electrical machines due to magnetomechanical coupling and magnetostriction[J].IEEE Transactions on Magnetics,2006,42 (4):971-974.
[9]Jerzy Podhajecki,Adrian Mot,Mariusz Korkosz.Comparison vibration due to Maxwell forces and magnetostriction in BLDC motor-dynamic analysis[J].Prace Naukowe Instytutu Maszyn,Napedów i Pomiarów Elektrycznych Politechniki Wrocawskiej,2008,62(28): 325-330.
[10]Pan Seok Shin,Hee Jun Cheung.A magnetostrictive force and vibration mode analysis of 3 kW BLDC motor by a magneto-mechanical coupling formulation[J].Journal of Electrical Engineering&Technology,2011,6(1):76-80.
[11]IEC/TR 62581,Electrical steel-Methods of measurement of the magnetostriction characteristics by means of single sheet and epstein test specimens[S].
Research on vibration and noise of permanentmagnet synchronousmotor w ith magnetostriction effects
HAN Xue-yan,ZHANG Zhe,WU Sheng-nan,CHEN Jian
(National Engineering Research Center for REPM Electrical Machines,Shenyang University of Technology,Shenyang 110870,China)
An important source of PMSM noise ismagnetostrictive vibration of themagnetic core.Based on the piezomagnetic laws,amagentic-mechanical coupling model was proposed which can take themagnetostrictive effect into account.Hypothetical and boundary conditions of the solving region were also provided.Using finite elementanalysis software,the vibration of a 11kW PMSM was calculated with ideal current supply andmeasured current supply,and whatneed to pointout is the calculation was done considering only electromagnetic force ormagnetostricive effect and both of them.And then,the acoustic field distribution around themotorwas analyzed.In order to verify themodel,the vibration and noisewere studied experimentally.The validity of the proposedmethod was confirmed by numerical calculation results and experimental results.Furthermore,thismethod which could help prediction the noise level in PMSM design step and seek new denoisemethods has great potential in the future application.
permanentmagnet synchronousmotor(PMSM);magnetostriction;magnetic-mechanical coupling;finite element analysis;vibration and noise
TM351
A
1003-3076(2015)01-0028-07
2014-08-05
国家科技支撑计划(2013BAE08B00)、国家自然科学基金(51307111)、辽宁省教育厅科学技术研究项目(L2013049)资助项目
韩雪岩(1979-),女,辽宁籍,副教授,博士,研究方向为特种电机及其控制技术;张哲(1988-),男,辽宁籍,硕士研究生,研究方向为永磁电机振动噪声。

