5阶CKF在捷联惯导非线性对准中的应用研究
黄湘远,汤霞清,武 萌
(装甲兵工程学院控制工程系,北京100072)
5阶CKF在捷联惯导非线性对准中的应用研究
黄湘远,汤霞清,武 萌
(装甲兵工程学院控制工程系,北京100072)
为了提高动基座下车载捷联惯导系统(strapdown inertial navigation system,SINS)的初始对准精度和缩短对准时间,在不进行粗对准的前提下,利用5阶容积卡尔曼滤波(cubature Kalman filter,CKF)完成非线性对准。针对3阶CKF滤波精度不高、5阶高斯厄密特滤波器计算量过大的问题,基于多项式逼近的思想详细推导了5阶球面径向容积规则,继而提出了5阶CKF并分析了该算法的滤波精度、采样量和数值稳定性,利用奇异值分解代替Cholesky分解来增强滤波稳定性。实验结果表明,该方法能够有效完成大失准角下的非线性对准,精度高于3阶CKF。
容积卡尔曼滤波;球面径向容积规则;初始对准;动基座
0 引 言
随着惯性导航技术的进步及应用环境的拓展,具备复杂环境下快速高精度的初始对准能力是捷联惯导系统(strapdown inertial navigation system,SINS)的基本需求之一。此时,线性初始对准方案受到了非常大的限制,基于大失准角模型的非线性对准方案受到越来越多的关注。
高斯非线性滤波器是非线性滤波的重要组成部分,其最优滤波框架需利用状态后验分布的一、二阶矩来获得当前时刻的最优状态估计。由于无法获得状态后验理论分布,只能通过状态的先验信息和近似算法来估计,从而构成了一些次优滤波器,如扩展卡尔曼滤波(extended Kalman filter,EKF)、高斯厄密特滤波(Gauss-Hermite quadrature filter,GHQF)、无迹卡尔曼滤波(unscented Kalman filter, UKF)、中心差分卡尔曼滤波(central difference Kalman filter, CDKF)、容积卡尔曼滤波(cubature Kalman filter,CKF)等[1-6]。
EKF使用Taylor展开对非线性函数进行线性截断,精度较低,容易发散;GHQF通过GH变换来逼近非线性积分,精度高,稳定性强,不过采样点多,计算量大,难以应用于高维滤波问题;UKF和CDKF采用Sigma点来计算均值与协方差,精度至少可达二阶[6];CKF基于球面径向容积规则(spherical radial cubature rule,SRCR)将非线性积分进行分解和逼近,能够达到3阶精度[4];CKF一经提出,就获得了大量应用[78]。为了提高CKF的滤波性能,从数值稳定性[4,9]、计算复杂度[1011]、滤波精度[5,12-13]等角度出发,出现了多种改进算法。
为了提高动基座下SINS的对准精度,从精度和计算量上综合考虑,基于3阶CKF推导了5阶SRCR和CKF,进行了性能分析和改进。对准结果表明,该方法能够完成任意失准角下的非线性对准,滤波精度高、稳定性强、计算量相对较小,具有重要的工程应用价值。
1 SINS非线性对准误差模型
导航坐标系n系为东北天(O-ENU)坐标系;载体坐标系b系为右前上(O-x yz)坐标系。系统航向角、俯仰角θ和横滚角γ,姿态矩阵为Cbn。水平失准角ΦE和ΦN及方位失准角ΦU,记为为速度误差,L,λ为纬度和经度。陀螺Δ误差为常值零漂εb加白噪声ωbg,加速度计误差为常值零偏b加白噪声ωba。
准静基座下或者依赖GPS/BD提供速度位置信息的阻尼SINS导航模式下,大失准角下非线性系统模型[14]为

式中

状态向量取

噪声向量取
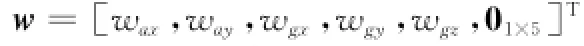

式中,H=[02×3,I2×2,02×5];v为测量噪声。
2 一些典型非线性高斯滤波器
设离散非线性系统为

式中,xk和zk分别为k时刻系统的状态量和观测量;f(·)和h(·)为已知任意函数;wk和vk分别为系统噪声和观测噪声,wk~N(wk;0,Qk)和vk~N(vk;0,Rk),且互相独立。
文献[1]基于高斯噪声假设和Bayes滤波估计原理推导了上述非线性系统的最优滤波框架,为

式中,^xk|k-1,^zk|k-1,Pxx,Pzz和Pxz参考文献[1,4]。
这些值均为如下形式的多维积分:
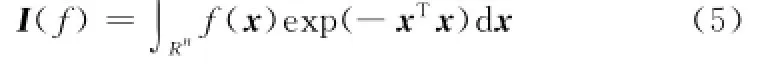
式中,f(·)为非线性函数;Rn为积分区域。
该框架将非线性滤波问题转化成非线性函数与高斯概率密度乘积的多维积分求解问题,求解积分式是非线性滤波的关键问题。一般情况下无法得到上述积分的解析值,需要求取数值近似解。不同的滤波算法对该积分值的求取思路和方法各不相同,典型算法有EKF、UKF、CDKF、CKF、GHQF等,各算法基本区别如下:
(1)基本原理:EKF基于Taylor展开和线性截断, UKF使用UT变换,CDKF采用中心差分和多项式插值来避免导数计算,CKF使用3阶SRCR逼近,GHQF利用GH变换逐层逼近。
(2)计算难点:EKF需计算繁琐的雅可比阵,其他算法需进行误差协方差阵Cholesky分解。
(3)采样点数:设系统维数为n,一次滤波过程中UKF需采样2n+1次,CDKF为2n+1次,CKF为2n次,GHQF的采样次数根据滤波精度而变,实现2m-1阶精度需进行mn次采样,计算量大,极易陷入维数灾难。
(4)滤波精度:EKF为一阶精度,UKF和CDKF达到二阶精度,CKF达到3阶精度,GHQF的精度根据需要设置。
(5)数值稳定性:GHQF和CKF积分公式绝对数值稳定,UKF和CDKF积分公式非绝对稳定,表明前两者的滤波稳定性强于后两者。
综上,CKF为数值稳定性强,滤波精度较高,计算量小的非线性滤波算法。为了进一步提高滤波精度,可将3阶SRCR提升到5阶,构建计算量远小于5阶GHQF的5阶CKF。
3 5阶CKF算法

式中,Un为n维单位超球面;σ(·)为Un上的元素。积分式I(f)可分离为spherical积分S(r)和radial积分R两部分,其中

3.1 5阶球面径向容积规则
令变量x=r y,其中yTy=1,r∈[0,∞),则全局范围内非线性函数积分I(f)在spherical-radial坐标系可写成
讨论积分式I(f)的数值解逼近精度时,一般使用简单多项式函数来逼近和分析。考虑多项式f(y)=yd11yd22…均为非负整数,次数为此时S(r)和
R转化为

理论证明,当S(r)和R的逼近精度达到m阶时,I(f)的逼近达到m阶精度。3阶CKF使用3阶球面径向容积规则,I(f)的逼近精度达到3阶,为了提高CKF的滤波精度,在此基础上推导5阶逼近算法。
3.1.1 spherical规则
S(r)的m阶逼近算法要求式(7)对所有|d|≤m的多项式应严格成立。
S(r)的计算可利用如下公式:
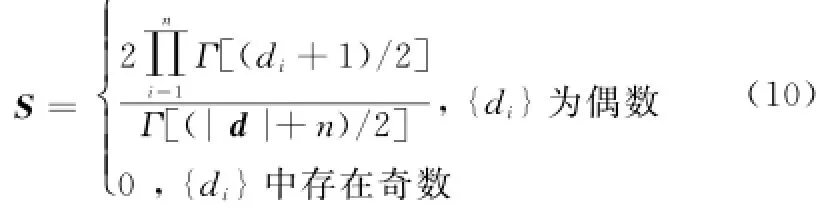
式(10)表明,当|d|为奇数时,{di}中必然存在奇数,此时S=0。当|d|为偶数时,S才可能不为零,此时需计算S。并不是所有的偶数阶多项式都需计算S;对于某多项式f(y)而言,对阶数{di}的排列顺序进行简单的置换形成的多项式,积分值S保持不变。当m=5时,需计算S值的典型形式有4种,分别为



两种采样方式均能使S(r)的逼近精度达到5阶,本质上没有太大区别。本文采取文献[5]中的采样方式,此时可用如下逼近方式求解spherical积分:

式中,[e]i、[s]i分别为[e]n、[s]n的第i列。
将|d|≤5时各典型形式代入式(11),得:


3.1.2 radial规则
radial积分R=∫∞
0S(r)rn-1e-r2d r的m阶逼近算法要求式(8)对所有不超过m阶的单项式S(r)=ri应严格成立。
当i为奇数时,由于I(f)的对称性可知,ωr,i的任意取值不会影响算法的逼近效果,因此只需考虑i为偶数时ωr,i的选取问题。此时,积分R的真实值可利用广义Gauss-Laguerre积分来计算,也意味着R的Nr采样逼近规则能够达到2(2Nr-1)+1阶精度[45]。
解此方程组,得
该方程组拥有无穷多个可能解,理论上方程组的任意解不会影响算法的逼近精度,但会影响算法的数值稳定性。为了获取最优解,可利用广义Gauss-Laguerre积分规则来求解该方程组。此时,r21和r22的最优值为多项式方程Ln2/2-1(x)=0的解[8],其中
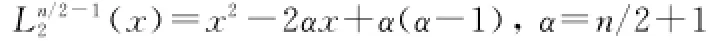
求解多项式方程Ln2/2-1(x)=0,有

为了获得R的5阶逼近,要求式(8)满足如下方程组:
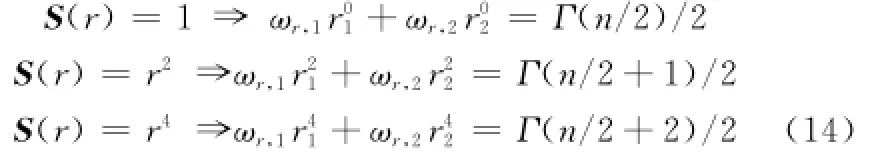
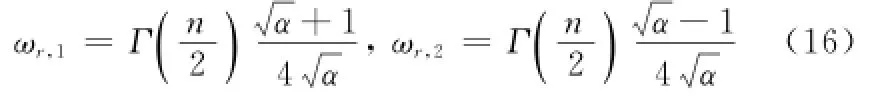
3.1.3 非线性函数积分
假设随机变量x~N(x;^x,Px),则任意函数f(x)的统计特性E f为

将其代入式(14),可以得到
式中,Sx为Px的Cholesky分解阵。
将5阶spherical规则和radial规则代入式(16),可得Ef的5阶精度的逼近方式:

图1表示R2空间中标准正态分布下3阶和5阶SRCR的采样点和计算权值。3阶SRCR采集某圆与坐标轴的交点,各采样点计算权值相同;5阶SRCR采集两圆与坐标轴的交点及其中点,计算权值不尽相同,对非线性函数的逼近更精确。由于采样点的计算权值相对较小,减小了采样个体对积分逼近的重要性,对奇异点具有抑制作用。5阶SRCR采样点较多,需16次,计算量较大,而3阶SRCR仅采样4次。

图1 SRCR采样点及权重
3.2 5阶CKF算法
将5阶SRCR和Guass-Bayes滤波框架结合起来,得到5阶CKF,具体如下。
3.2.1 时间更新

(2)计算容积点

3.3 CKF算法性能分析
滤波精度:5阶CKF能够达到5阶滤波精度,高于3阶CKF,与5阶GHQF精度相当。
采样点数:3阶CKF的采样点数2n个,5阶CKF相对较多,为4n2个,系统维数较大时,算法计算量较大。相对于5阶GHQF所需的3n个采样点,计算量依然可以接受。
数值稳定性:任何滤波方法都由积分公式导出,为了衡量积分公式的数值稳定性,定义稳定因子I[16]为I=∑|ωi|(19)式中,ωi为各采样点的权值。
当I>1时,积分公式是数值不稳定的,会引入大量的截断误差,可能导致误差协方差阵失去正定性,对非线性滤波器来说是致命的。CKF中I=1,说明其积分计算是绝对数值稳定的,意味着CKF的滤波稳定性强;UKF中,当n>3时,I=(2n-3)/3,说明UKF在处理高维问题时精度较差甚至滤波失败;5阶CKF中,当n>5时,I=3(n-2)/ (n+2),在处理高维问题时可能导致滤波失败。非线性对准模型中,n=10,此时5阶CKF不是绝对稳定的,当初始协方差阵设置不当时,Pk失去正定性的可能性大于CKF,表明5阶CKF的稳定性弱于CKF。
3.4 5阶CKF算法的改进措施
CKF算法进行多次滤波之后,由于计算舍入、模型失准等原因,可能导致Pk失去正定性,使得滤波发散。文献[4]为了解决3阶CKF的滤波稳定问题,推导了Square-root CKF算法。由于需对采样点的权值进行平方根运算,而高维问题中5阶CKF的采样权值出现了较多的负数,Squareroot思想难以直接迁移过来。为了增强5阶CKF的稳定性,可利用协方差矩阵Pk的奇异值分解代替Cholesky分解[17]。由于奇异值分解的数值计算鲁棒性较强,有利于提高算法的数值稳定性。由于奇异值分解的计算量大于Cholesky分解,因此算法优先选择Cholesky分解,当分解失败时使用奇异值分解。
4 实验仿真与验证
4.1 摇摆基座下初始对准仿真
假设陀螺的常值漂移为0.02(°)/h,随机漂移0.01(°)/h,加速度计的常值零偏0.1 m g,随机零偏0.05 m g。纬度L= 39.84°,经度λ=116.12°。战车在某颠簸路面行驶,其姿态[18]为

对于车载捷联惯导来说,水平姿态一般不超过10°,从而能够获得相对较小的初始水平失准角。设初始失准角为Φ=(10°,10°,40°)T,分别使用3阶和5阶CKF算法进行非线性对准仿真,仿真时间700 s。由于对准过程中水平姿态估计与速度误差直接相关,可观测性强,对准速度快,精度高,故不做重点分析。
图2给出了200 s后两种算法的方位失准角误差估计曲线。滤波速度上,图2表明两种算法的估计速度相当,均需300 s以上的时间,说明高阶逼近算法不能增加系统的可观测性,对加快滤波速度无能为力。

图2 摇摆基座下方位失准角误差估计曲线
滤波精度上,图2说明5阶CKF略高于3阶CKF。为了定量分析滤波精度,表1给出了对准结束前10 s对准结果平均值,结果表明:水平对准误差ΦE和ΦN相对于方位对准误差ΦU是小量,这与初始对准极限精度公式是一致的;5阶CKF的方位对准精度提高了略0.03°,表明了算法的有效性。

表1 对准误差比较
计算量上,3阶CKF每次滤波过程中采样20次,5阶CKF需采样400次,5阶GHQF需采样59 049次。表明5阶CKF相对3阶CKF采样计算量较大,相对5阶GHQF较小。在某些需要高精度的场合中5阶CKF具有重要意义。为此,需结合具体应用,在计算量和对准精度之间权衡利弊,选择合适的方案。
4.2 战车行进过程中的初始对准实验
现代战争的突然性和快速机动性要求战车惯导系统能够在行进过程中快速完成高精度对准。此时,粗对准需较长时间或者难以实现,可考虑大失准角下的非线性对准问题。
实验室采用高精度光纤陀螺SINS,安装在某步兵战车上,战车行进过程中使用高精度GPS/BD导航芯片提供速度、位置参考信号。实验过程中,战车的行进路线如图3所示,时间为2 h,行进中有上下坡、颠簸路面、转弯、停车等多种环境。任意选取4段900 s的数据进行对比分析,实验过程中由于粗对准需要较长时间,系统不进行粗对准,直接进行非线性精对准。由于无法提供惯导的真实姿态作为参考,使用SINS/GPS组合导航结果作为参考姿态。行进过程中,GPS/BD信号良好。

图3 战车行进中的位置曲线
图4反应了4次动基座方位对准的均方根误差曲线,可以看出动基座下两种滤波的方位失准角收敛速度相当,约400 s左右均能达到0.2°左右,约600 s后误差曲线趋于稳定,且5阶CKF的精度高于3阶CKF。表2给出了对准结束前10 s对准结果平均值,发现方位对准精度由上3阶CKF的0.141 9°提高到了0.110 7°。说明,将5阶CKF应用到车辆行进时惯导系统的初始对准过程中,短时间内能够获得和CKF相当的精度,一段时间后能够取得更好的结果。
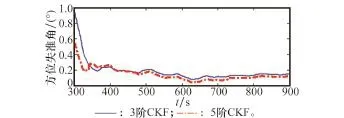
图4 动基座方位对准均方根误差曲线

表2 动基座对准均方根误差
为了减少非线性滤波的计算量,最有效的方法是降低系统维数。其中3阶CKF算法计算量为O(n),5阶CKF算法的计算量为O(n2),表明随着系统维数的减小,5阶算法的计算量减小量更为显著,对缩短滤波计算时间更有意义。静基座下非线性对准中,可将状态向量x分为线性部分xl和非线性部分xn,利用CKF-Kalman混合滤波进行处理,有效降低计算量[19]。5阶CKF也可类似处理,形成5阶CKF-Kalman混合滤波器,计算量降低效果更为明显,不过动基座下非线性对准还得进行进一步的研究。
5 结 论
基于非线性滤波的非线性对准问题是当前研究的热点。CKF利用球面容积径向规则对多维非线性积分进行逼近,摆脱了对非线性模型的依赖,数值稳定性强,计算量较小,在非线性对准中具有自身的优点。然而,其3阶滤波精度导致初始失准角偏大时对准精度不够高。高阶滤波算法意味着大的计算量,基于5阶球面容积径向规则的高阶CKF能够兼顾滤波精度和计算复杂度,在非线性对准中具有重要的应用价值。
[1]Ito K F,Xiong K Q.Gaussian filter for nonlinear filtering problem[J].IEEE Trans.on Automatic Control,2000,45(5):910-927.
[2]Julier S J,Uhlmann J K,Durrant-Whyte H F.Unscented filtering and nonlinear estimation[J].Proc.of the IEEE Aerospace and Electronic Systems,2004,92(3):401-422.
[3]Arasaratnam I,Haykin S,Hurd T R.Cubature Kalman filtering for continuous-discrete systems:theory and simulations[J]. IEEE Trans.on Signal Processing,2010,58(10):4977-4993. [4]Arasaratnam I,Haykin S.Cubature Kalman filters[J].IEEE Trans.on Automatic Control,2009,54(6):1254-1269.
[5]Jia B,Xin M,Cheng Y.High-degree cubature Kalman filter[J]. Automatica,2013,49:510-518.
[6]Zhang Z Y,Hao Y L,Zhang X.Performance evaluation of sigma point Kalman filter for SINSinitial alignment[J].Journal of Chinese Inertial Technology,2010,18(6):639-644.(张召友,郝燕玲,张鑫.Sigma点Kalman滤波在惯性导航初始对准中的性能评估[J].中国惯性技术学报,2010,18(6):639-644.)
[7]Sun F,Tang L J.Initial alignment of large azimuth misalignment angle in SINS based on CKF[J].Chinese Journal of Scientific Instrument,2012,33(2):327-333.(孙枫,唐李军.基于CKF的SINS大方位失准角初始对准[J].仪器仪表学报,2012, 33(2):327-333.)
[8]Pesonen H,Piche R.Cubature-based Kalman filters for positioning[C]∥Proc.of the 7th Workshop on Positioning,Navigation and Communication,2010:45-49.
[9]Tang X J,Wei J L,Chen K.Square-root adaptive cubature Kalman filter with application to spacecraft attitude estimation[C]∥Proc.of the 15th International Conference on Information Fusion, 2012:1406-1412.
[10]Dahmani M,Meche A,Keche M,et al.Reduced cubature Kalman filtering applied to target tracking[C]∥Proc.of the 2nd International Conference on Control,Instrumentation and Automation,2011:1097- 1101.
[11]Qian H M,Ge L,Huang W,et al.Reduced dimension CKF algorithm and its application in SINS initial alignment[J].Systems Engineering and Electronics,2013,35(7):1492-1497. (钱华明,葛磊,黄蔚,等.降维CKF算法及其在SINS初始对准中的应用[J].系统工程与电子技术,2013,35(7):1492-1497.)
[12]Lin X G,Xu S S,Xie Y H.Multi-sensor hybrid fusion algorithm based on adaptive square-root cubature Kalman filter[J]. Journal of Marine Science and Application,2013,12:106-111.
[13]Pei H L,Sanjeev A,Tharaka A,et al.A Gaussian-sum based cubature Kalman filter for bearings-only tracking[J].IEEE Trans.on Aerospace and Electronic Systems,2013,49(2): 1161-1176.
[14]Yan G M,Yan W S,Xu D M.Application of simplified UKF in SINS initial alignment for large misalignment angles[J]. Journal of Chinese Inertial Technology,2008,16(3):253 265. (严恭敏,严卫生,徐德民.简化UKF滤波在SINS大失准角初始对准中的应用[J].中国惯性技术学报,2008,16(3):253-265.)
[15]Wang S Y,Feng J C,Tse C K.Spherical simplex-radial cubature Kalman filter[J].IEEE Signal Processing Letters,2014, 21(1):43 46.
[16]Wu Y X,Hu D W,Wu M P,et al.A numerical-integration perspective on Gaussian filters[J].IEEE Trans.on Signal Processing,2006,54(8):2910-2921.
[17]Zhang Q Z,Zhang S B,Liu Z P,et al.Robust cubature Kalman filter based on SVDand its application to integrated navigation[J]. Control and Decision,2014,29(2):341-346.(张秋昭,张书毕,刘志平,等.基于奇异值分解的鲁棒容积卡尔曼滤波及其在组合导航中的应用[J].控制与决策,2014,29(2):341-346.)
[18]Wang Y G,Yang J S,Yu Y,et al.On the move alignment for SINS based on odometer aiding[J].Systems Engineering and Electronics,2013,35(5):1060-1063.(王跃钢,杨家胜,蔚跃,等.基于里程计辅助的SINS动基座初始对准方法[J].系统工程与电子技术,2013,35(5):1060-1063.)
[19]Zhao X J,Liu G B,Wang L X,et al.Augmented cubature Kalman filter/Kalman filter integrated algorithm[J].Infrared and Laser Engineering,2014,43(2):647-653.(赵曦晶,刘光斌,汪立新,等.扩展容积卡尔曼滤波-卡尔曼滤波组合算法[J].红外与激光工程,2014,43(2):647-653.)
Application of 5th-degree CKF in SINS nonlinear initial alignment
HUANG Xiang-yuan,TANG Xia-qing,WU Meng
(Department of Control Engineering,Academy of Armored Force Engineering,Beijing 100072,China)
In order to improve alignment precision and reduce time for the initial alignment of strapdown inertial navigation system(SINS)under the moving base,a new method that nonlinear alignment with 5th-degree cubature Kalman filter(CKF)without coarse alignment is proposed.Because of lower accuracy of 3rd-degree CKF and too much calculation work of the 5th-degree Gauss-Hermite quadrature filter,a new sampling rule named 5th-degree spherical radial cubature rule based on polynomials approximation and a new CKF with 5thdegree accuracy from this rule are deduced.The filter accuracy,sampling points,numerical stability are analyzed.The singular value decomposition algorithm is used to replace Cholesky decomposition for stronger stability.The experiment results demonstrate that the method is able to complete nonlinear alignment on big misalignment angles and has higher estimation accuracy than 3rd-degree CKF.
cubature Kalman filter(CKF);spherical radial cubature rule;initial alignment;moving base
U 666.1
A
10.3969/j.issn.1001-506X.2015.03.25
黄湘远(1988-),男,博士研究生,主要研究方向为非线性滤波、惯性导航。
E-mail:huangxiangyuan.623@163.com
汤霞清(1965),男,教授,博士,主要研究方向为惯性导航、战车火控。
E-mail:tangxiaqing_001@163.com
武 萌(1981-),女,讲师,博士研究生,主要研究方向为导航、制导与控制。
E-mail:wumeng0326@126.com
网址:www.sys-ele.com
1001-506X(2015)03-0633-06
2014 05 14;
2014 10 16;网络优先出版日期:2014 11 05。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20141105.1500.001.html
军队计划项目资助课题

