基于偏差分离原理的卫星执行机构故障诊断
李冬柏,陈雪芹,李诚良
(1.哈尔滨工业大学卫星技术研究所,黑龙江哈尔滨150080; 2.小卫星技术国家地方联合工程研究中心,吉林长春130033; 3.中国科学院长春光学精密机械与物理研究所,吉林长春130033)
基于偏差分离原理的卫星执行机构故障诊断
李冬柏1,2,陈雪芹1,2,李诚良3
(1.哈尔滨工业大学卫星技术研究所,黑龙江哈尔滨150080; 2.小卫星技术国家地方联合工程研究中心,吉林长春130033; 3.中国科学院长春光学精密机械与物理研究所,吉林长春130033)
提出一种同时估计输入时滞和控制输入故障的方法。首先,基于偏差分离的思想,分别建立含有输入时滞和控制输入故障的一般控制系统与卫星姿态控制系统的数学模型。其次,基于二阶Kalman滤波对控制输入故障以及输入时滞进行估计。最后,对所提出的方法进行了数学仿真验证,特别地,基于“快舟一号”卫星控制系统半物理仿真平台进行了半物理仿真验证,证明了方法的可行性和有效性。
故障诊断;时滞;卫星;姿态控制
0 引 言
基于Friedland提出的偏差分离估计[13]进行偏差估计的方法一直广受关注并在多个领域进行了应用。Friedland所提出的偏差分离估计算法,其基本思想就是将线性系统的状态与参数(偏差)分别独立估计,然后将估计结果进行合成,得到系统状态的最优估计,偏差分离估计算法也称为二阶Kalman滤波算法。基于该方法描述故障时,物理意义明确,可以利用二阶Kalman滤波算法直接得到故障大小的估计结果,而无需通过其他参数间接描述故障程度。
文献[4 8]利用该方法建立系统故障模型进行系统故障检测与诊断以及容错控制研究,并取得了大量研究成果。还有其他一些学者对基于该方法的故障诊断及容错控制进行了相关研究,例如文献[9-15]。文献[16-20]也将这一描述方法多次应用于卫星姿控系统故障诊断与容错控制研究。
近年来,编队卫星飞行控制备受关注,其中编队卫星的姿态协同控制在合成孔径雷达成像和空基干涉测量等任务中起着重要的作用。然而编队飞行时卫星之间通信存在时间延迟导致卫星的协同控制不能满足任务的要求。因此,本文在进行系统建模时也考虑到输入时滞的影响。
K-Chabir等在文献[15]中提出了一种同时估计网络控制系统中的时滞与故障大小的方法。受K-Chabir的启发,本文建立了含有输入时滞和控制输入故障的一般控制系统数学模型,这一系统模型可应用于常规的控制系统描述。并针对性地建立了含有输入时滞和执行机构故障的卫星姿态控制系统数学模型。针对该模型,基于偏差分离原理能够有效估计出执行机构故障大小和输入时滞大小。
基于“快舟一号”卫星控制系统半物理仿真平台,对本文设计的系统模型以及故障诊断方法进行半物理仿真验证,证明了本文采用的基于偏差分离原理的故障诊断方法用于线性系统输入时滞估计和控制输入故障估计的有效性。与作者之前基于有效性因子的卫星姿态控制系统故障诊断的相关研究成果相比,其原理更加简单,除了估计出系统状态,还可直接估计出控制输入故障,且能同时估计出输入时滞,半物理仿真验证也说明其具有实际应用价值。
1 带有输入时滞与控制输入故障的系统建模
基于偏差分离的思想,考虑带有未知常数偏差的线性系统状态方程为
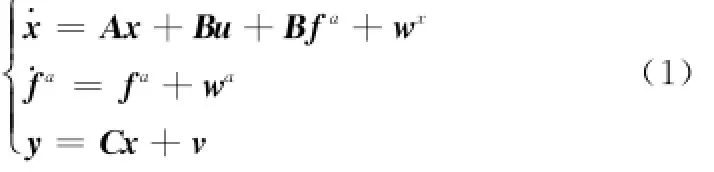
式中,fa是由fai(i=1,…,l)组成的向量,fa表示未知常数偏差;B表示偏差分布矩阵;Bfa表示控制输入故障;A表示系统矩阵;C表示测量矩阵;wx、wa和v是彼此不相关的零均白噪声,对应的协方差矩阵分别为Qax>0,Qa>0,R>0。
假设控制输入时滞为τ,而且满足
τ<T式中,T为离散控制系统的采样时间。考虑时间延迟之后一个采样周期内控制信号记为在这种控制输入条件下,离散的控制系统状态方程可记为
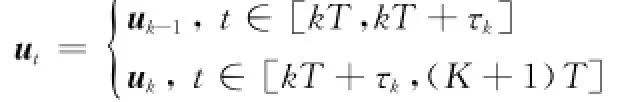
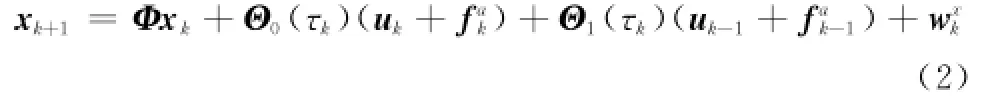
其中

对于形如式(1)的系统模型,可以直接利用上式进行离散化。
令

则状态方程可以重新写为
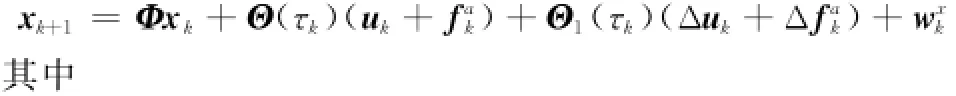
采用反作用飞轮作为系统的执行机构,采用星敏感器测量卫星的姿态角信息,陀螺测量姿态角速度信息。令状


状态方程可以写为

又由于
状态方程中的ΦBΔukτk类似一个未知的输入,从而令

则最终状态方程为
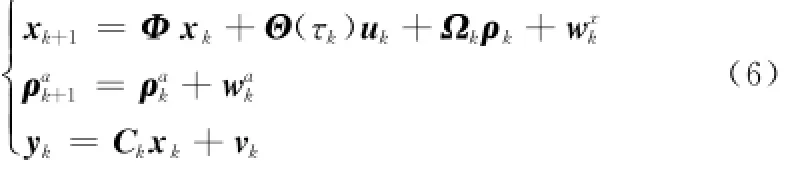
2 含执行机构故障的卫星姿态控制系统的建模

设卫星本体相对惯性系的角速度为

定义卫星转动角动量为H,卫星姿态动力学方程表示为

式中,u和Td分别为星体所受控制力矩和外部干扰力矩,分别记为

定义轨道角速度为

忽略转动惯量矩阵中的惯量积,动力学方程式(9)展开为态变量为


根据卫星姿态动力学方程式(13),不考虑外部干扰力矩,仅考虑高斯白噪声影响,建立系统状态方程为
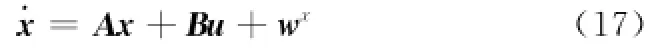
式中
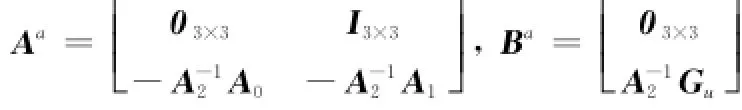
在上述状态方程中考虑执行机构故障时,卫星姿态控制系统的状态方程能够写为式(1)的形式

式中,fa为3×1的矩阵。
由于系统的状态均可观测,因此系统的观测方程为

式中,C是6×6的单位矩阵;v是白噪声。将状态方程观测方程离散化后得到形如式(6)的形式。
3 执行机构故障估计
通常采用扩展状态观测器/滤波器进行线性/非线性系统的状态/参数估计。然而,由于大多数动态系统都可以描述成偏差分离的形式,在过去的40年里,Friedland的偏差分离原理也广泛地应用于各类线性/非线性系统状态/参数估计。本文也将采用这一方法进行执行机构故障估计,在线性系统状态和参数估计方法的基础上,根据确定性等价原理,将非线性项Ak(xk)中的状态值xk利用状态估计值^xk
代替,~Φ=eAk(~xk)T,详细迭代过程为
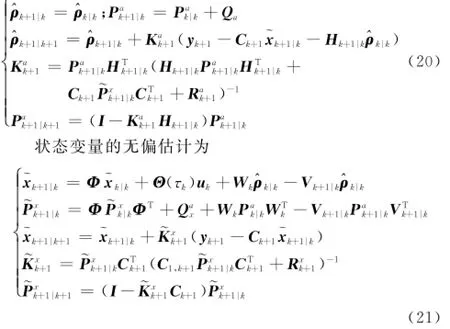
建立未知常数偏差、输入时滞与状态变量之间的耦合关系

此时,利用式(20)~式(22)可以得到经过补偿的状态估计值以及协方差矩阵

以上迭代过程可以得到状态变量估计值,即姿态角和姿态角速度、控制输入时滞τk以及执行机构故障Θ(τk)fak。
4 数学仿真验证
在Matlab/Simulink下建立卫星姿态动力学方程、执行机构模型(含故障)、敏感器模型以及一个PD控制器模型,将前文所述的执行机构故障估计器与之组成闭环控制系统,将执行机构故障估计器的状态估计结果作为PD控制器的输入,通过闭环仿真验证执行机构故障估计器在卫星姿态控制系统执行机构故障诊断中应用的有效性。
卫星姿态控制系统的仿真参数如下:
(1)PD控制器的参数分别为

(2)仿真步长为:0.25 s;
(3)星体主惯量矩阵取为

(4)飞轮最大角动量为:±1.25 N·m·s(飞轮转速±6 000 rpm时);
(5)飞轮最大输出力矩为:0.1 N·m;
(6)初始姿态角速度
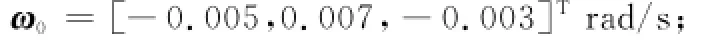
(7)初始姿态角:α0=[-0.05,0.1,0.1]T;
(8)卫星轨道角速度:ωo=0.001 rad/s;
(9)状态变量初始值:x0=06×1,f0=06×1;
(10)传播矩阵初始值:Px0=I6×6,Pa0=I6×6;
(11)协方差矩阵

卫星的执行机构的故障具体表现为执行机构输入命令与实际输出之间的差别。飞轮的加性故障体现为摩擦力矩的突然增大、电子元器件失效等导致的飞轮输出力矩的增大或者减小,仿真中共设置了两个加性故障,第一次的故障出现在x轴,-0.05N·m,时间是从60 s到250 s;第二次的故障出现在y轴,0.03N·m,时间是300 s到450 s。故障估计结果如图1所示,执行机构输出力矩仿真结果如图2所示。
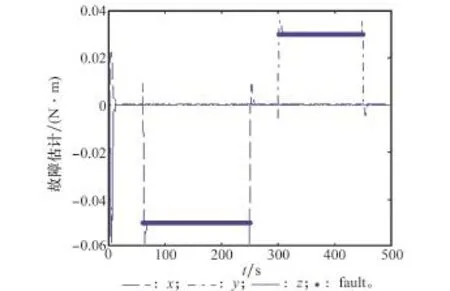
图1 执行机构故障估计结果

图2 执行机构输出力矩
实际的卫星姿态控制系统的控制周期比较长,如果能够估计出来控制时滞的大小,然后对其进行补偿,将能够显著改善控制系统的性能。在仿真验证中加入的控制时滞大小为0.04 s,利用二阶Kalman滤波算法估计出来的时滞大小如图3所示。由图3可知,时滞的估计结果还是比较满意的,但需要较长时间才能趋于真实值。卫星姿态角、姿态角速度仿真结果分别如图4和图5所示。

图3 输入时滞估计结果
5 半物理仿真验证
“快舟一号”卫星控制系统半物理仿真平台如图6所示,该平台验证了“快舟一号”卫星姿态控制精度能满足飞行任务的高精度控制要求。该仿真平台采用的飞轮、陀螺均为型号卫星正样备份产品,该平台能提供一个真实的卫星实验验证系统。仿真平台总体结构如图7所示,是基于MATLAB/Simulink在xPC目标实时环境下开发的实时仿真平台,可以很方便地完成执行机构故障诊断、姿态控制系统测试。

图4 姿态角

图5 姿态角速度

图6 半物理仿真平台
半物理仿真的试验方案为:利用气浮转台模拟卫星绕俯仰轴的转动,另外两个轴为数学模型。俯仰轴的角度由转台测角仪测量,角速度由光纤陀螺测量,在气浮转台上配置两个反作用飞轮,一个作为执行机构,另一个用于模拟执行机构故障(也可采用地面控制台模拟飞轮故障)。仿真采用的两个飞轮是试验三号卫星反作用飞轮正样备份件。真实的敏感器、执行机构、气浮转台、“快舟一号”卫星姿态控制算法以及本文设计的执行机构故障估计器组成了俯仰通道闭环半物理仿真系统。俯仰通道初始角度和角速度均为零,目标姿态角为10°,目标姿态角速度为0。控制周期500 ms,数据采样周期50 ms。
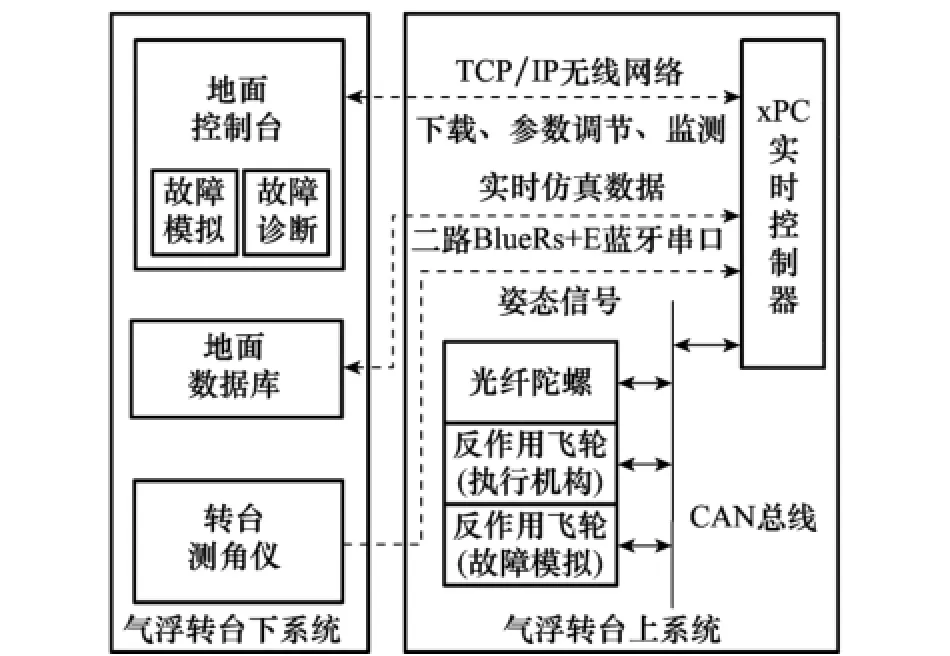
图7 半物理仿真系统总体结构图
飞轮模拟执行机构故障的实际输出结果如图8所示,模拟两段加性故障,一段为32.25 s至82.10 s,+0.01N·m,第二段为82.15 s至仿真结束,-0.01N·m。基于本文偏差分离原理的执行机构故障估计结果如图9所示,同时估计出的时滞如图10所示。图11为俯仰轴姿态角信息,为了保持数据的真实性,未处理图中的野值点。图12为俯仰轴姿态角速度信息。

图8 飞轮模拟执行机构故障输出

图9 执行机构故障估计结果
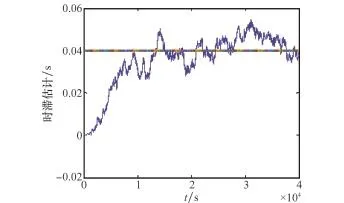
图10 时滞估计结果

图11 姿态角
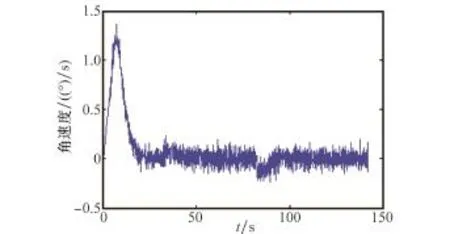
图12 姿态角速度
6 仿真结果分析
在数学仿真中,如图1和图2所示,故障估计算法能准确估计出执行机构故障,如图3所示,故障估计算法能准确估计出时滞的大小,但估计结果达到稳态值的时间较长,如图4和图5所示,由执行机构估计器、PD控制算法以及卫星姿态动力学组成的闭环数学仿真系统,能够准确估计出执行机构故障、时滞外,还能保持卫星的姿态稳定,卫星的姿态稳定度长时间内不受执行机构加性故障影响,但姿态指向精度持续受到执行机构加性故障影响。
在半物理仿真中,如图8和图9所示,故障估计算法能准确估计飞轮模拟的故障,虽然仿真曲线不如数学仿真曲线理想,但其趋于稳态值的时间短,具有实际应用价值,如图10所示,故障估计算法能准确估计出时滞,且与数学仿真结果图3一样,其趋于稳态值的时间较长,而且通过仿真发现,当时滞参数小于一个控制周期时,其对姿态控制系统的影响很小,其原因为单个卫星姿态控制时受时滞影响的因素较少,而该方法应用于编队卫星飞行控制时效果应更明显。
如图11和图12所示,与数学仿真结果一致,本俯仰轴半物理仿真系统能够准确估计飞轮模拟的执行机构故障、输入时滞,且俯仰轴姿态控制稳定,姿态指向精度持续受到执行机构加性故障影响,姿态稳定度长时间内不受执行机构加性故障影响。
以文献[18]为例,本文研究结果与作者前期同类文献相比,本文设计的方法可直接得到故障的大小,而此前作者的同类研究是利用偏差分离原理建立基于有效性因子的故障模型,然后利用有效性因子的变化作为控制器设计的依据,其研究重点为故障诊断与容错控制的集成性以及控制系统的鲁棒性,但无法准确得到故障的大小。本文结合前期理论研究和实际工程需要,设计基于偏差分离原理的故障诊断方法,克服了前期研究方法无法准确得到故障大小这一缺陷,除了估计出系统状态,还可直接估计出控制输入故障,可便于直接对故障器件进行隔离,此外本文方法还能同时估计出输入时滞,经过实际型号的半物理仿真系统验证说明其具有实际应用价值。
文中采用姿态角表示卫星姿态,采用姿态四元数建立系统模型时,文中所述方法同样适用。
7 结 论
基于偏差分离原理进行控制输入故障和输入时滞估计,原理简单,易于应用。本文建立了含有控制输入故障和输入时滞的线性系统模型,针对该模型利用偏差分离原理设计了故障估计算法,并针对性地将这一算法应用到了卫星姿态控制系统中,数学仿真和半物理仿真验证了将其应用于卫星姿态控制系统时的可行性和有效性,未来有望实现实际工程应用,提高卫星姿态控制系统的可靠性和时效性。根据故障的表示方法,故障能够分为乘性故障与加性故障,本文考虑的是加性故障,但同样适用于乘性故障,仅需修改系统模型中的故障模型表示方法。
[1]Friedland B.Treatment of bias in recursive filtering[J].IEEE Trans.on Automatic Control,1969,14(4):359-367.
[2]Ignagni M B.An alternate derivation and extension of Friedland.s two-stage Kalman estimator[J].IEEE Trans.on Automatic Control,1981,26:746-750.
[3]Ignagni M B.Optimal and suboptimal separate-bias Kalman estimators for a stochastic bias[J].IEEE Trans.on Automatic Control,2000,45:547-551.
[4]Wu N E,Zhang Y M,Zhou K M.Control effectiveness estimation using an adaptive Kalman estimator[C]∥Proc.of the IEEE International Symposium on Intelligent Control,1998:181-186.
[5]Wu N E,Zhang Y M,Zhou K M.Detection,estimation,and accommodation of loss of control effectiveness[J].International Journal of Adaptive Control and Signal Processing,2000,14: 775-795.
[6]Yu X,Jiang J.Hybrid fault-tolerant flight control system design against partial actuator failures[J].IEEE Trans.on Control Systems Technology,2012,20(4):871-886.
[7]Zhang Y M,Jiang J.Integrated design of reconfiguration faulttolerant control systems[J].Journal of Guidance,Control and Dynamics,2000,1(24):133-136.
[8]Fan J H,Zhang Y M,Zheng Z Q.Robust fault-tolerant control against time-varying actuator faults and saturation[J].IET Control Theory and Applications,2012,6(14):2198 2208.
[9]Wang D J.Study on schemes of fault detection and diagnosis& fault tolerant control[D].Changchun:Jilin University,2004. (王德军.故障诊断与容错控制方法研究[D].长春:吉林大学,2004.)
[10]Xiao B,Hu Q L,Shi P.Attitude stabilization of spacecrafts under
actuator saturation and partial loss of control effectiveness[J].IEEE
Trans.on Control Systems Technology,2013,21(6):2251-2263. [11]Xiao B,Hu Q L,Zhang Y M,et al.Fault-tolerant tracking control of spacecraft with attitude-only measurement under actuator failures[J].Journal of Guidance,Control and Dynamics,2014,37(3):838-849.
[12]Xiao B,Hu Q L,Singhose W,et al.Reaction wheel fault compensation and disturbance rejection for spacecraft attitude tracking[J].Journal of Guidance,Control and Dynamics, 2013,36(6):1565 1575.
[13]Benosman M,Lum K Y.Application of absolute stability theory to robust control against loss of actuator effectiveness[J]. IET Control Theory and Applications,2009,3(6):772-788.
[14]Jamouli H,Sauter D.Adaptive estimation of loss control effectiveness based on fault detection filter[C]∥Proc.of the 18th Mediterranean Conference on Control&Automation Congress, 2010.
[15]Chabir K,Sauter D,Al-salami I M,et al.Two-stage Kalman filter for simultaneous fault and delay estimation in networked control systems[C]∥Proc.of the 18th Mediterranean Conference on Control&Automation Congress,2010.
[16]Chen X Q,Zhang Y C,Geng Y H,et al.Satellite attitude control system on-orbit reconfigurable fault-tolerant control based on the control effectiveness factor[J].Journal of Astronautics, 2007,28(1):94-98.(陈雪芹,张迎春,耿云海,等.基于控制有效性因子的卫星姿态控制系统在轨重构容错控制[J].宇航学报,2007,28(1):94-98.)
[17]Chen X Q,Wang F,Zhang Y C,et al.Application of effective
ness factors to integrated FDD and FTC of satellite attitudecontrol systems[J].Acta Aeronautica et Astronautica Sinica, 2009,30(3):476-483.(陈雪芹,王峰,张迎春,等.有效性因子在卫星姿控系统集成故障诊断与容错控制中的应用研究[J].航空学报,2009,30(3):476-483.)
[18]Chen X Q,Ma Y H,Wang F,et al.Research on improved integrated FDD/FTC with effectiveness factors[J].Journal of Systems Engineering and Electronics,2012,23(5):768 774.
[19]Li C L,Chen X Q,Jia Q X,et al.FDD of the attitude control system of satellite with actuator fault and time delay via Two-Stage Kalman Filter[C]∥Proc.of the 5th International Conference on Mechanical and Electronics Engineering,2013.
[20]Chen X Q,Li C L,Wang F,et al.Satellite attitude control system actuators additive fault estimation with two-stage Kalman filter[P].China:CN201310268646.3,2013-06-28.(陈雪芹,李诚良,王峰,等.一种利用二阶卡尔曼滤波算法估计卫星姿态控制系统执行机构加性故障大小的方法[P].中国:CN20131026-8646.3,2013- 06-28.)
陈雪芹(1982-),通信作者,女,副研究员,博士,主要研究方向为故障诊断与容错控制。
E-mail:cxqhit@163.com
李诚良(1989-),男,工程师,硕士,主要研究方向为控制系统故障诊断、卫星姿态估计。
E-mail:budhit@qq.com
Fault diagnosis of satellite actuator based on bias-separated theory
LI Dong-bai1,2,CHEN Xue-qin1,2,LI Cheng-liang3
(1.Research Center of Satellite Technology,Harbin Institute of Technology,Harbin,150080,China; 2.National&Local United Engineering Research Center of Small Satellite Technology, Changchun,130033,China;3.Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun 130033,China)
An estimation method of input delay and control input fault is proposed.At first,based on the bias-separated theory,a normal control system model and a satellite attitude control system model with input delay and control input fault are set up respectively.Then,the input delay and control input fault can be estimated by the two-stage Kaman filter.Finally,the simulation of the method in a satellite attitude control system with actuator fault and input time delay illustrates the effectiveness of the proposed approach.Mathematical simulation and a real-time simulation based on the“KUAIZHOU-1”satellite control system hardware-in-theloop simulation platform are performed to validate that the method is suitable and effective respectively.
fault diagnosis;delay;satellite;attitude control
V 448.22
A
10.3969/j.issn.1001-506X.2015.03.21
李冬柏(1980-),男,副研究员,主要研究方向为卫星姿态轨道控制系统设计。
E-mail:lidongbai@hit.edu.cn
网址:www.sys-ele.com
1001-506X(2015)03-0606-07
2014 05 09;
2014 10 28;网络优先出版日期:2014 11 05。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20141105.1510.006.html
国家自然科学基金(61104026)资助课题

