贮存可用度约束下的可修系统寿命评估与优化
马小兵,杨 力
(1.北京航空航天大学可靠性与系统工程学院,北京100191;2.北京航空航天大学可靠性与环境工程技术国防科技重点实验室,北京100191)
贮存可用度约束下的可修系统寿命评估与优化
马小兵1,2,杨 力1
(1.北京航空航天大学可靠性与系统工程学院,北京100191;
2.北京航空航天大学可靠性与环境工程技术国防科技重点实验室,北京100191)
针对长期贮存复杂可修系统的特点,提出一种以可用度为约束的系统贮存寿命评估方法。该贮存系统由三类部件串联构成:第一类部件为高可靠产品,具有给定故障时间分布且不进行检测;第二类部件为等时定检维修产品,且修复如新;第三类部件为定期预防性更换产品,更换周期与检测周期相同。在分析上述三类部件瞬态贮存可用度变化规律基础上,推导了此类系统的平均贮存可用度,并以其作为约束条件,建立了该类系统贮存寿命的评估与优化模型,给出了满足系统寿命最大化的检测与更换策略。
可修系统;寿命评估;贮存可用度;定期检测;定期更换
0 引 言
根据国军标451A-2005定义,使用寿命是指产品使用到从技术上或者经济上考虑不宜继续使用,而必须报废或者大修时的寿命单位数。而贮存作为一种特殊的使用形式,其寿命的技术衡量指标可采用贮存可用度。对于可修贮存系统,贮存可用度影响因素主要包括贮存系统的故障规律、检测维修策略和保障资源等。
____现阶段,国内外关于可用度开展了较多研究。在单部件可用度方面,文献[1-3]建立了定检产品的可用度模型,其中检测维修时间忽略。文献[4-8]研究了检测维修时间不可忽略时可用度的变化规律。而在多部件可用度方面,文献[9]基于多类相互独立的部件的可用度研究了费用优化问题。文献[10-11]分析了失效相互影响下的两部件和多部件可修系统的平均可用度。文献[12-14]建立了包含不同寿命分布组件的系统混合检测和替换模型,并推导了系统的平均可用度。
然而,上述文献均进行的是工作状态的可用度研究,对于贮存环境下的复杂系统可用度变化规律缺少研究。为此,本文基于实际的贮存情况,对由三类故障分布与维护策略均不相同的典型部件所构成串联系统的贮存可用度开展了具体研究。三类部件的维护方式分别为:无检测、定期检测并维修、定期更换。根据更新理论,分别推导了各类部件的瞬态可用度,并在考虑维修和更换时间差异性的基础上,给出了该系统的瞬态可用度和平均可用度。
本文在相关研究基础上提出一种以系统平均贮存可用度为约束的贮存寿命评估和优化方法。若经过一段贮存期,系统平均贮存可用度降低到某一规定的阈值,则系统必须进行整体大修或报废处理,而到达该阈值的时间即为系统贮存寿命。可通过对系统检测周期进行优化,实现系统贮存寿命最大化的目标,并通过算例给出了模型的优化计算结果。
1 基本假设
假设1 系统由三类不同部件串联组成,为简化模型,假定每一类均为单个部件。各类部件失效时间服从不同的分布,且相互独立,互不影响。
假设2 三类部件于同一时刻开始贮存,设为零时刻。
假设3 第二类部件每隔固定周期进行检测,检测时间忽略不计。
假设4 第三类部件的更换周期与第二类部件的定期检测周期相同。
假设5 维修和更换期间贮存系统均处于非正常贮存状态,即瞬态可用度为零。
假设6 维修和更换时间均为不可忽略的固定值。
2 系统贮存寿命定义
记XS(t)为贮存系统在t时刻的状态随机变量,即

则系统的瞬态贮存可用度是指系统在规定的贮存条件下,在规定的时刻具备规定功能的概率,则系统在t时刻的瞬态贮存可用度定义为

系统的平均贮存可用度是指在贮存时间[0,t]内能工作的时间所占的比例,可根据瞬态可用度进行推导

对于由三类典型部件串联构成的可修贮存系统,贮存寿命可定义为

即若经过一段时间的贮存,系统平均贮存可用度首次下降到某一规定的可用度阈值Aα,则认为该贮存系统不能满足规定的技术要求,必须进行报废或者大修等操作。而这一段的贮存时间TS即为系统的贮存寿命。
需要指出的是,选取平均贮存可用度作为贮存寿命的约束条件是由于其递减的平滑性,波动幅度较小,而系统瞬态贮存可用度由于存在零点,且波动幅度较大,不适宜作为寿命约束。
3 贮存可用度模型
对于该串联贮存系统,无法直接根据更新理论得到系统在[0,t]内的平均可用度,需要通过系统的瞬态可用度来进行转换。下面首先研究各类部件的瞬态贮存可用度。
3.1 第一类部件瞬态贮存可用度模型
此类部件可靠性较高,无需进行检测和维修更换。在不考虑维修更换等因素的情况下,该类部件在任意时刻的瞬态可用度即为其可靠度,即
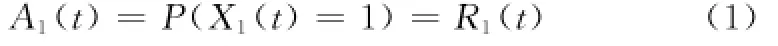
3.2 第二类部件瞬态贮存可用度模型
假定该类部件从零时刻开始贮存,初始可靠度为1。每隔固定时间T对部件进行定期检测。一旦检测到故障,则立即进行维修。经过Tc(0<Tc<T)的时间修复如新,继续贮存。检测更换策略如图1所示。

图1 第二类部件的检测维修策略
设该类部件的故障时间分布函数为F2(t),可靠度函数为R2(t)。推导可知,该类部件在任意时刻t的瞬时贮存可用度A2(t)可表示为

式中,k=1,2,…;ci=i T+Tc。
推导过程如下。设Tf为该类部件第一次故障发生时间,Tf*为第一次维修完成时间,Tl为最后一次故障发生时间,Tl*为第二类部件最后一次维修完成时间。
(1)当0<t≤T时,无维修发生,可用度即为其可靠度,故有

(2)当T<t≤c1时,部件可能处在未故障或故障维修两种状态下,注意到部件从发生故障到维修结束前均不可用,故其瞬态可用度可表示为


(3)当ck<t≤ck+1时,对于该类部件在t之前发生过故障且在t时刻处于完好的概率为

3.3 第三类部件瞬态贮存可用度模型
由于该类部件容易故障,故采用定期预防性更换策略,其更换周期和第二类部件的检测周期相同,均为T。更换需要固定时间TR(0<TR<T)。更换策略如图2所示。

图2 第三类部件的更换策略
第三类部件的瞬态贮存可用度为

式中,k=1,2,…;dk=k T+TR。
推导过程如下。
(1)当0<t≤T时,部件更换还未开始,故A3(t)= P(X3(t)=1)=R3(t)。
(2)当k T<t≤dk(k=1,2,…)时,该类部件正在进行更换,此时部件处于不可用状态,故A3(t)=P(X3(t)=1)=0。
(3)当dk<t≤(k+1)T时,该类部件最近的更新时刻,即上一次更换完成时刻为dk,而0<t-dk≤T,故t时刻的可用度为

3.4 系统瞬态贮存可用度模型
可修贮存系统由第3.1~3.3节中的三类部件串联构成,且三类部件之间相互独立、互不影响。因此,当任意一类部件处于不可用状态时,整个系统也将处于不可用度状态。因此,系统整体在任意时刻t的瞬态贮存可用度为AS(t)=A1(t)×A2(t)×A3(t)(4)
由于第二类部件为检测后的修复性维修,其所需时间一般大于第三类部件的预防性更换时间,故假定Tc>TR,此时系统的瞬态贮存可用度可表示为

式中,k=1,2,…。
4 系统贮存寿命优化方法研究
注意到若系统平均贮存可用度无法降至临界值Aα,或者收敛于某一大于Aα的值,则对贮存寿命的约束条件不存在。因此,首先需要证明该系统贮存可用度收敛于某一小于Aα的值,证明过程如下。
对于第一类部件,其在无限时间区间内的稳态贮存可用度为

而系统由三类部件串联构成,因此系统平均贮存可用度必然低于第一类部件的平均贮存可用度,故在无限时间区间上系统的稳态贮存可用度必然也收敛于0,即
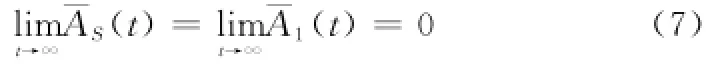
故系统平均贮存可用度收敛于0,因而其必然在某一时刻下降到Aα。
从便于工程实施的角度考虑,贮存寿命一般定为检测/更换周期的整数倍。若m T<TS≤(m+1)T,即若贮存寿命处于(m T,(m+1)T)之间,则可将贮存寿命近似为最后一次检测时刻T'S=(m+1)T。
则贮存寿命最大值的数学形式为

即通过对检测/更换周期T进行优化,可使系统平均贮存可用度降低到阈值的时间所需最长,从而实现系统贮存寿命最大化的优化目标。下面通过数值算例来对优化结果进行分析,并通过仿真进行验证。
5 算例与结果分析
5.1 贮存可用度算例
系统贮存时间以月为单位。假设第一类部件故障时间服从指数分布,失效率λ1=1/2 500/月;第二类部件故障时间服从威布尔分布,参数为η2=100月,m2=1.8,失效率λ2(t)=1.8×t0.8/1001.8/月,故障维修所需时间Tc为0.2个月;第三类部件故障时间服从指数分布,失效率为λ3= 1/600/月,更换所需时间TR为0.1个月。通过式(1)~式(3),得到三类部件在不同周期下的瞬态贮存可用度。
当检测周期为12个月时,第二类部件瞬态贮存可用度变化规律如图3所示。可以看到,其震荡幅度较大,且最小瞬态贮存可用度逐渐收敛于某一定值。此外,由于维修期间部件不可用,故在首个检测周期之后,最大瞬态贮存可用度无法达到1。
当更换周期为12个月时,第三类部件瞬态贮存可用度变化规律见图4。可以看到,在更换期间瞬态贮存可用度为0,并且除了首个更换周期外,其余周期内的可用度变化规律相同。
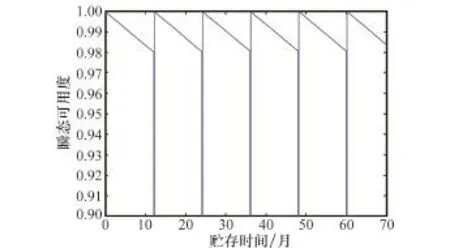
图4 第三类部件瞬态贮存可用度(更换周期12个月)
采用式(5)计算系统瞬态贮存可用度,并通过数值积分,得到系统在不同检测周期下的平均贮存可用度,误差为10-4。检测和更换周期均为12个月时系统的平均贮存可用度变化规律见图5。可以看到,随着贮存时间增加,整体上平均贮存可用度呈递减的趋势。而在局部,除首个周期外,其余检测/更换周期内平均贮存可用度在呈先增后减的变化趋势,但是变化幅度逐渐减小。
分析可知,由于系统第二类部件故障时间服从威布尔分布,失效率随时间逐渐增大,导致系统失效率也逐渐增大,使维修带来的可用度提升逐渐减小。此外,在第4节中已证明系统平均贮存可用度随时间增大收敛于0,故在图中呈递减态势。

图5 系统平均贮存可用度(检测周期和更换周期均为12个月)
5.2 系统贮存寿命优化算例
给定平均贮存可用度阈值Aα=0.9作为贮存寿命TS的约束条件。则可根据第5.1节中得到的不同检测/更换周期下的平均可用度值,对T进行优化运算,得到系统最长贮存寿命T*S。
假设检测周期最小为1个月,最大为24个月,步长为0.1个月。计算可知,当检测周期为6.1个月时,贮存寿命达到最长,为183个月。贮存寿命和检测周期之间的关系如图6所示。可以看到,随着检测周期的增大,局部范围内系统贮存寿命呈现周期性的先增后减锯齿形变化规律,而从整体上看,贮存寿命先迅速增大,随后缓慢的减小,存在最大值。
对寿命变化规律分析可知,当检测周期很短时,由于存在维修时间和更换时间等固定的不可用时间,使正常贮存时间在总时间中的比重降低,平均贮存可用度迅速下降,因而贮存寿命较短。而当检测周期过大时,由于第二类部件的检测维修以及第三类部件的更换均不够及时,故障导致的不可用时间过长,贮存可用度不符合要求,贮存寿命同样较短。因此,合理的检测/更换周期大小是延长贮存寿命的关键。

图6 不同检测周期下的贮存寿命
5.3 仿真验证
仿真根据系统总贮存时间和总不可用时间来计算系统的平均可用度,并根据设置的平均可用度阈值计算贮存寿命。
各项基本参数值参见第5.1节。需要生成的随机变量包括服从指数分布的第一、第三类部件故障时间f1、f3和服从威布尔分布的第二类部件故障时间f2。仿真运行次数K=10 000。仿真流程如图7所示。
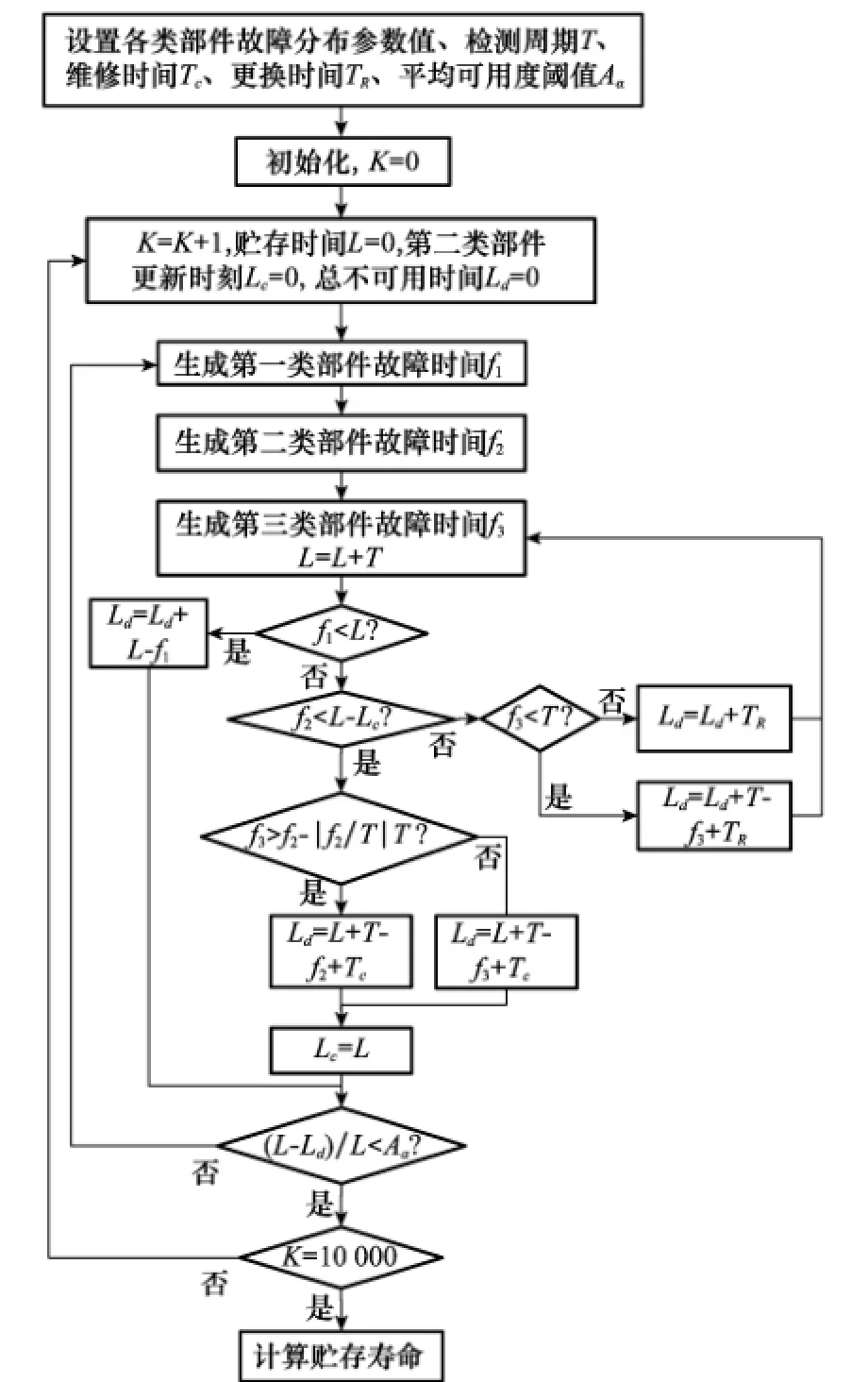
图7 仿真流程图
部分仿真和运算结果的对比如表1所示,其中检测周期、维修时间和更换时间分别取不同的值,Aα=0.9。通过对比可以看到,贮存寿命的解析模型和仿真模型结果基本吻合,从而验证了其准确性。

表1 贮存寿命模型计算值和仿真值
6 结 论
本文提出了一种以平均贮存可用度为约束的贮存寿命评估与优化方法。给出了贮存寿命等定义的数学表达式。通过更新理论,分别推导了定期检修、定期更换和无维护产品的瞬态贮存可用度。基于维修和更换时间的差异性,研究了系统贮存可用度的变化规律。以此为基础,证明了贮存可用度对贮存寿命约束的合理性,并确定了以检测周期为优化变量的贮存寿命最大化方法。算例结果表明,系统平均贮存可用度局部呈周期性变化,整体上递减,且收敛于零。系统寿命随检测周期增加呈先递增后递减的变化规律,因而存在最优检测(同时也为更换)周期,使系统到达贮存可用度阈值的时间最长,即实现贮存寿命最大化。
[1]Cui L R,Zhao X,Shen J,et al.An availability model for storage products under periodical inspections[J].International Journal of Reliability,Quality and Safety Engineering,2010,17(2):89-103. [2]Cui L R,Du S,Hawkes A G.A study on a single-unit repairable system with state aggregations[J].Trans.on IIE,2012,44 (11):1022-1032.
[3]Taghipour S,Banjevic D.Periodic inspection optimization models for a repairable system subject to hidden failures[J].IEEE Trans.on Reliability,2011,60(1):275 284.
[4]Sarkar J,Sarkar S.Availability of a periodically inspected system under perfect repair[J].Journal of Statistical Planning and Inference,2000,91(1):77-90.
[5]Biswas A,Sarkar J,Sarkar S.Availability of a periodically inspected system,maintained under an imperfect-repair policy[J]. IEEE Trans.on Reliability,2003,52(3):311-318.
[6]Cui L R,Xie M.Availability of a periodically inspected system with random repair or replacement times[J].Journal of Statistical Planning and Inference,2005,131(1):89-100.
[7]Tang T.Failure finding interval optimization for periodically inspected repairable systems[D].Toronto:University of Toronto,2012.
[8]Tang T,Lin D,Banjevic D,et al.Availability of a system subject to hidden failure inspected at constant intervals with nonnegligible downtime due to inspection and downtime due to repair/replacement[J].Journal of Statistical Planning and Inference,2013,143(1):176-185.
[9]Taghipour S,Banjevic D,Jardine A K S.Periodic inspection optimization model for a complex repairable system[J].Reliability Engineering and System Safety,2010,95(9):946-952.
[10]Golmakani H R,Moakedi H.Periodic inspection optimization model for a two-component repairable system with failure interaction[J].Computers&Industrial Engineering,2012,63 (3):540 545.
[11]Golmakani H R,Moakedi H.Periodic inspection optimization model for a multi-component repairable system with failure interaction[J].The International Journal of Advanced Manufacturing Technology,2012,61(1/4):295-302.
[12]Scarf P A,Cavalcante C A V.Hybrid block replacement and inspection policies for a multi-component system with heterogeneous component lives[J].European Journal of Operational Research,2010,206(2):384-394.
[13]Wang W,Banjevic D,Pecht M.A multi-component and multi-failure modeinspection model based on the delay time concept[J].Reliability Engineering and System Safety,2010,95(8):912-920.
[14]Fei S M.Research on storage availability modeling and optimization methods of materiel[D].Beijing:Beihang University, 2013.(费思邈.装备可用度建模与优化方法研究[D].北京:北京航空航天大学,2013.)
Life evaluation and optimization for a repairable system under the constraints of storage availability
MA Xiao-bing1,2,YANG Li1
(1.School of Reliability and Systems Engineering,Beihang University,Beijing 100191,China; 2.National Defense Key Laboratory of Science&Technology on Reliability&Environmental Engineering,Beihang University,Beijing 100191,China)
According to the character of complex long-term repairable storage systems,a method for evaluating their storage lives under the restriction of availability is presented.Such systems are composed of three kinds of serial components.The first kind of component has a high reliability with a given fault time distribution,and there are no inspections scheduled for it.The second kind of component undergoes periodic inspections,and once found failed,it is repaired to a condition as a new one.The third kind of component is preventively replaced periodically with the same cycle as the second kind.By analyzing the transient availability of each component respectively,the average availability of the whole repairable storage system is derived.Using it as a restriction,the evaluation and optimization model for the storage life of the system is established and the optimal maintenance strategy which maximizes the storage life is given.
repairable system;life evaluation;storage availability;periodic inspection;periodic replacement
TB 114.3
A
10.3969/j.issn.1001-506X.2015.03.15
马小兵(1978-),男,副教授,博士,主要研究方向为可靠性工程。
E-mail:maxiaobing@buaa.edu.cn
杨 力(1990-),男,硕士研究生,主要研究方向为可靠性建模分析。E-mail:yl19900709@126.com
网址:www.sys-ele.com
1001-506X(2015)03-0572-05
2014 02 11;
2014 07 31;网络优先出版日期:2014 10 19。
网络优先出版地址:http:∥w ww.cnki.net/kcms/detail/11.2422.TN.20141019.2343.002.html
国家自然科学基金(61104133)资助课题

