高超声速目标雷达回波脉内运动模型
徐雪菲,廖桂生
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071)
高超声速目标雷达回波脉内运动模型
徐雪菲,廖桂生
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071)
针对线性调频脉冲压缩雷达体制下高超声速目标回波信号建模问题,采用目前常用的停走模型,由于忽略了目标在一个脉冲持续时间内(简称脉内)的运动,不能真实反映目标回波特点,高超声速目标回波信号的脉冲压缩输出存在较严重的主瓣偏移并展宽的问题,严重影响目标信号的积累与检测。对此,提出了高超声速目标回波信号的脉内运动模型,理论分析和数值仿真均表明了高超声速目标的回波信号采用脉内运动模型的必要性。在典型参数下,采用脉内运动模型比采用停走模型的脉冲压缩增益提高3 d B以上。
回波模型;高超声速;脉内运动;脉冲压缩雷达
0 引 言
高超声速飞行器是一类新式作战武器,其最大的特点是飞行速度极高,是美国实现“全球一小时打击”计划的重要武器,对我国国土安全造成了严重威胁。目前,全世界对高超声速临近空间飞行器加紧研制,飞行器马赫数越来越高,现已有对马赫数为20甚至更高的飞行器的试飞实验。如果要求从远距离探测这类高超声速隐身目标,对雷达而言,将面临极大的挑战。其中,对目标回波信号进行相干积累以提高雷达接收机的信噪比是一个难题。
通常,在建模与分析脉冲压缩雷达接收的运动目标回波信号时,广泛采用停走(stop and go,SAG)模型,即认为目标在一个脉冲持续时间内(简称脉内)的运动可以忽略不计,而只考虑了脉冲之间的时延及多普勒效应,这样的简化处理尤其给合成孔径雷达(synthetic aperture radar,SAR)成像处理带来了很大的方便[1-3]。后来,人们发现这种SAG模型的近似,给一些应用场合带来误差。文献[4]针对星载双站合成孔径雷达,研究了SAG模型假设带来的斜距误差及其对成像和干涉处理的影响,并提出了该斜距误差可以近似等效为合成孔径慢时间的一次函数形式,因而给出以卫星位置、速度和加速度表示的等效斜距误差计算公式。文献[5]分析了调频连续波SAR由于大的重复周期和100%的信号占空比,目标运动导致SAG模型产生较大误差。文献[6]分析了SAG模型下星载SAR几何校正误差问题,提出了持续运动模型星载SAR几何校正方法。
雷达为提高分辨力和回波信号信噪比,通常发射脉冲信号的时宽带宽积较大,在脉冲持续时间内,目标高速运动可能导致回波产生较大的影响。然而,由于SAG模型一直被雷达界广泛采用,很少涉及到脉内运动可能对这种SAG模型带来误差,或者都认为这种误差可以接受,因而目前还没有文献仔细研究脉内运动究竟带来多大的误差,对通常的脉冲压缩雷达和合成孔径成像雷达的距离像等造成何等程度的影响。文献[7-8]针对多项式相位表示的高速机动目标回波信号的运动补偿,直接把多普勒频移以及变速运动等项加入信号的载波线性项上进行分析(同时忽略了运动对线性调频信号中二次项的影响),得出了多普勒运动引起脉冲压缩谱偏移,机动目标运动引起谱展宽。其实,文献[7-8]把运动目标的回波延时在一个脉冲持续时间内按常数来处理,相当于目标运动在一个脉冲持续时间内忽略不计,这本质上就是“SAG模型”。
通过理论公式推导和数值仿真分析,发现采用目前常用的SAG模型,高超声速目标回波信号的脉冲压缩输出存在较严重的主瓣偏移并展宽的问题,严重影响目标信号的积累与检测。对此,本文建立了目标脉内运动的回波模型,为区别于以前的SAG模型,这里给出的模型称为脉内运动(inner pulse motion,IPM)模型。理论分析和数值仿真均表明高超声速临近空间飞行器目标的回波信号采用脉内运动模型的必要性。在典型参数下,采用脉内运动模型比采用SAG模型的脉冲压缩增益提高3 dB以上。
本文余下内容安排如下:第1节给出传统目标回波信号的SAG模型;第2节给出高速目标回波信号IPM模型;第3节给出两种模型下对回波信号进行脉冲压缩处理结果,给出了详细的数学公式;第4节给出了高超声速点目标脉冲压缩和扩展目标高分辨一维距离像的数值仿真实验结果;最后给出本文的结论。
1 目标回波信号SAG模型
设脉冲压缩(pulse compression,PC)雷达发射信号为线性调频脉冲,脉冲持续时间为Tp,单位为s,调频斜率为K,单位为Hz/s。其基带信号复数形式为
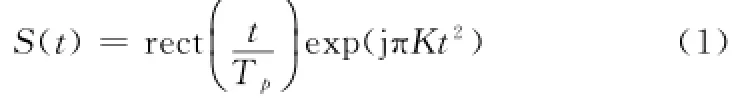
射的时间变量。
假定雷达波束照射到一个高超声速目标,其相对于雷达的斜距离历程随时间变化用函数R(t)表示。通常R(t)可以用一个多项式表达[4]:
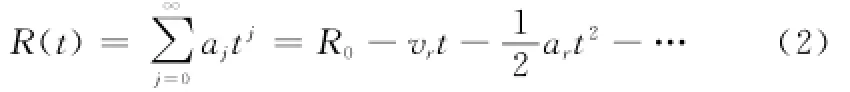
式中,R0为目标相对雷达的初始斜距;vr为目标的径向速度,沿着径向靠近雷达为正,远离为负;ar为目标的径向加速度,沿着径向朝着雷达方向为正,远离为负。
雷达界普遍认为线性调频脉冲对目标运动的多普勒容限比较大,通常采用SAG模型,即认为目标相对于雷达的运动在一个脉冲时间宽度内所产生的位置变化很小,可以忽略不计,而只考虑相邻脉冲间目标相对雷达运动产生的位置变化。换言之,雷达发射脉冲波形从其上升沿照射到目标,到其下降沿离开目标的期间内认为目标一直处于“停”的状态,不考虑目标在脉冲时间宽度内的运动,直到下一个脉冲再次照射到目标时,目标才跳跃到另一个位置。在这样的假设下,第m个脉冲的照射的目标时,目标相对于雷达的斜距历程为

式中,m=0,1,2,…。在传统SAG模型中,对于同一个脉冲,目标的延时τm是一个不变的定值,由慢时间tm=m Tr确定,可以表示为

暂时假定目标为理想点目标,依据现有的SAG模型,则接收回波基带信号解析表达式[1]为
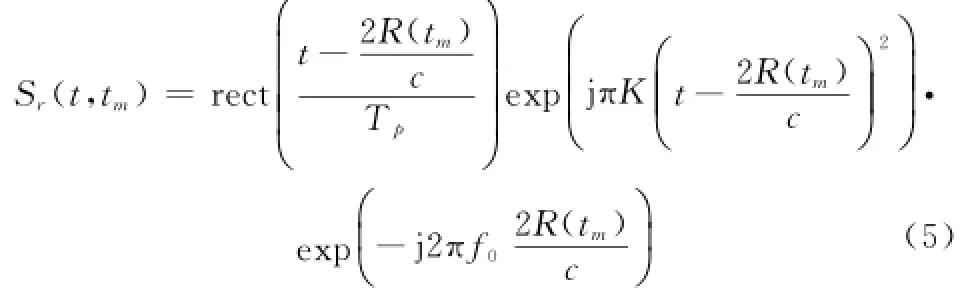
式中,c为光速;f0为发射载波频率;Tr为脉冲重复周期;tm为慢时间的时刻;t为全时间变量。将式(4)代入式(5),得到

2 高速目标回波信号IPM模型
对于高超声速目标的检测,一方面,目标相对于雷达运动的速度马赫数高达数十甚至20~30;另一方面,为了提高雷达作用距离和提高距离分辨率及探测精度,采用大时宽带宽积的线性调频信号是需要的。在这种情况下,高速目标的运动在一个脉冲时间宽度内所产生的位置变化将不可忽视,但是目前文献上给出信号回波模型,基本上还是上述SAG模型,虽然提到了目标在一个脉冲时间宽度_内的运动情况,然而并没有真正在其信号模型中反映出来[78]。
IPM模型则认为运动目标在一个脉冲时间宽度内,其与雷达之间的斜距历程R(t)是时变的,不再同式(3)那样为常数。R(t)仍可用式(2)表示,相应的IPM模型下的回波信号表示如下

式中,t为全时间变量,其在第m个发射脉冲的脉冲时间宽度Tp内连续变化的范围为t∈[tm,tm+Tp]。
IPM模型下,虽然目标与雷达之间的斜距R(t)仍可用式(2)表示,其回波信号模型式(7)与式(5)似乎形式相同。但是,其内涵发生了根本性的变化。
在IPM模型中,目标回波在脉冲时间宽度内的延时可表示为

区别于τm,式(8)中τIPM为高速运动目标在脉冲宽度内的延时,是一个由目标瞬时位置确定的变量。即在同一个脉冲内,延时是一个关于目标相对雷达斜距的连续函数,和脉冲时间宽度这段时间有着连续的对应关系,这样就可以表示出目标运动对脉冲时间宽度内回波脉冲的影响。容易看出,SAG模型是IPM模型中的特例,即当τIPM=τm(常数),也就是在脉冲时间宽度内各个时刻相对于发射脉冲时间的延时为同一个常数τm。换言之,在这段时间内,目标静止不动。将式(8)代入式(7),得

为了便于理解,可用一个特例来说明,假若高速目标做匀速运动,其相对于雷达的斜距历程可以表示为

将式(10)代入式(9),得

在时域,可以得到τIPM的变化范围为
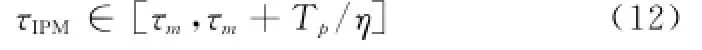
脉冲时间关系用下面示意图1表示。

图1 SAG模型与IPM模型对比示意图
图1表示径向速度vr>0(目标靠近雷达)和vr<0(目标远离雷达)两种情况下脉冲回波时间宽度的变化。即回波脉冲在同一时刻接收,但脉冲持续时间有变化。按照从上到下的顺序依次是:发射脉冲时间宽度、SAG模型下脉冲回波时间宽度和IPM模型下脉冲回波时间宽度。可以发现,在SAG模型中,认为脉冲时间宽度和发射脉冲一致,均为Tp;而真实的IPM模型表明,脉冲回波时间宽度受到目标运动产生的多普勒效应的影响而发生改变。对比SAG模型与IPM模型的回波信号脉冲持续时间发现,描述同一个脉冲从发射到照射到目标返回被雷达接收,IPM模型存在脉冲时间宽度的压缩/展宽,压缩/展宽系数为η。
3 脉冲压缩性能分析
下面分析目标高速运动对脉冲压缩性能的影响。为便于理解,下面仅针对目标做高速匀速直线运动情况下,推导上述两种模型回波信号频谱,来考察脉冲压缩匹配滤波器响应与压缩性能。这些结果推广到非匀速运动情况是容易的。
3.1 两种模型回波信号频谱
利用驻定相位原理(principle of stationary phase, POSP)[13],容易推导两个模型下回波信号的频谱。首先给出SAG模型的频谱如下:

分析对比SAG模型与IPM模型的回波信号频谱发现,用真实的IPM模型描述时,脉冲回波的频谱(即带宽)由KTp变为KTpη,频率中心由f0变为,可以由下面的示意图2表示。
图2给出了发射脉冲频谱变化范围(即带宽),在径向速度vr>0(目标靠近雷达)和vr<0(目标远离雷达)两种情况下带宽的变化。按照从上到下的顺序依次是:发射脉冲带宽、SAG模型回波脉冲带宽和IPM模型回波脉冲带宽。在SAG模型中,认为脉冲带宽和发射脉冲一致,均为K Tp。而真实的IPM模型表明,接收回波脉冲的脉冲时间宽度受到目标运动产生的多普勒效应的影响而发生改变。带宽展宽/压缩系数η倍,而且信号的中心频率有偏移,偏移的大小为顺便指出,时域压缩η倍,则频域展宽η倍。

图2 SAG模型与IPM模型下回波信号频谱对比示意图
3.2 两种模型下脉冲压缩处理对比
脉冲压缩就是雷达系统中通过对发射的宽脉冲调制信号进行匹配滤波压缩处理成为窄脉冲的过程,以解决提高雷达作用距离和距离分辨率间的矛盾。
通常,雷达用发射波形对回波信号进行匹配处理,式(14)给出了发射线性调频信号的频谱公式。如果目标回波信号满足理想的SAG模型,即频域表示为式(13)或时域表示为式(5),则匹配滤波器的频域响应为发射脉冲信号频谱的共轭,即

因此,SAG模型下的脉冲压缩的频域实现如下
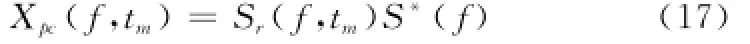
容易看到,由于消去了相位中的二次项,改写得到

对式(18)进行逆傅里叶变换,即

得到SAG模型下脉冲压缩之后的结果为

然而,对于高超声速运动目标不再满足SAG模型,服从IPM模型。如果仍用发射脉冲信号频谱的共轭作为脉冲压缩的频域响应,将无法实现对回波信号的“匹配”处理。

进一步整理可以得到


对比式(18)可以看到,这里除矩形窗函数的宽度有压缩/展宽、矩形窗中心有偏移之外,匹配之后的频谱一次相位存在平移,即频偏,为2在此基础上同样存在压缩/展宽,系数为η。更重要的是,式(22)中,这个“匹配”滤波并没有把IPM模型回波脉冲的二次相位消除,其二次相位变为与1的大小关系,越接近1,则二次相位产生的影响越小。对式(22)进行逆傅里叶变换,得到脉压处理后的时域信号为
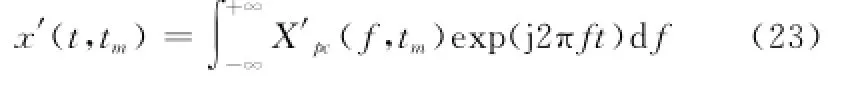
由于式(22)存在二次相位,这时脉压处理输出的时域式(23)不再得到与SAG模型一样的sinc函数。


对¯X'pc(f,tm)进行逆傅里叶变换到时域,可以得到x'(t,tm)=

实际上,我们应该用与IPM模型相匹配的脉压滤波器。由上面分析可知,如果目标为匀速直线运动而且其速度已知,则通过式(15),可以由发射的LFM信号,求得与IPM模型回波相匹配的脉压滤波器频域响应,即用^H(f)与IPM模型频谱进行匹配,并做逆傅里叶变换到时域

则匹配滤波输出为一sinc函数:

式(28)表明,通过式(26)表示的匹配滤波器,同样可以消除IPM模型下频谱相位中的二次项,再进行逆傅里叶变换,同样得到类似理想的SAG模型下脉冲压缩结果。
顺便指出:脉冲压缩匹配滤波器要求对目标回波信号完全匹配,可以获得理想的脉压结果,即标准的sinc函数。上述针对IPM模型提出的脉压滤波器要求已知目标运动速度,实际上是难以实现的。在目标运动参数未知情况下,脉压匹配滤波仍是一个有待研究的问题。这里提出一个原理性的方法,假定高超声速目标的运动速度范围大致可知,则可按速度分段设计一组滤波器,用该组滤波器对回波信号进行滤波处理和对比选优,并可进一步缩小速度范围和分段精度,找到满足条件的匹配滤波器。
另外,还可以设计一种自适应可调参数滤波器,有关工作后续介绍。
4 数值仿真实验
本节按实际物理过程,生成高超声速目标回波信号,然后按SAG模型和IPM模型分别给出点目标和扩展目标脉压处理的数值仿真实验结果。之所以给出扩展目标高分辨一维距离像脉压处理结果,目的是分析高超声速运动对合成孔径雷达(包括高超声速目标ISAR或星载SAR)的一维距离像处理的影响。
4.1 点目标情况
参数设置:以高速目标相对于雷达做径向的匀速直线运动为例,信号中心频率f0=3 GHz(S波段),信号带宽300 MHz,其他参数随图给出。
图3给出了按SAG模型和IPM模型下处理点目标回波信号的脉压结果,目标沿径向远离雷达,速度大小分别取10马赫、25马赫和40马赫,脉宽分别取0.1 ms和1 ms。由图3可见,随着目标速度的提高或者脉冲宽度增大,SAG模型与目标实际运动存在较大的失配,导致脉压输出不仅增益严重下降,而且峰值位置发生严重的偏移。图3中IPM模型只给出了目标速度为25马赫的情况,其他情况类似。

图3 速度为10、25和40马赫的点目标在两种模型脉压结果(脉宽分别取0.1 ms和1 ms)
通过表1可以看到,对于实际高速运动的目标回波,速度为25马赫,脉宽0.1 ms,经典模型脉压损失约3.6 d B;速度为25马赫,脉宽1 ms,经典模型脉压损失约16.4 dB。这对检测时信噪比积累影响是很大的。而且,脉压的峰值位置发生偏移,这将会对测距造成误差。

表1_脉压峰值_
4.2 扩展目标情况
参数设置:信号中心频率为f0=3 GHz(S波段),带宽300 MHz,LFM信号的脉宽分别取0.1 ms和1 ms,扩展目标为10 m的直线,1 m间隔设置一个点目标,共计10个点目标,目标速度大小为25马赫。
图4和图5分别给出了脉宽为0.1 ms和1 ms情况下脉压处理仿真结果,由图4、图5可以看出,对于真实的高速运动目标回波情况,如果仍用SAG模型进行脉冲压缩,高分辨一维距离像效果较差。
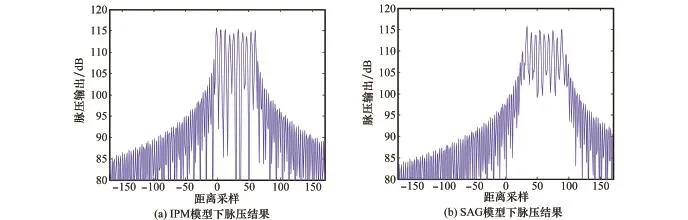
图4 扩展目标在脉宽为0.1 ms、速度为25马赫下两种模型回波脉压处理结果

图5 扩展目标在脉宽为1 ms、速度为25马赫下两种模型回波脉压处理结果
5 结 论
本文通过对传统的SAG模型和IPM模型下脉冲压缩的分析与比较表明,对于高速目标,即使不考虑机动性(高阶项影响)的情况下,直接对雷达接收回波信号按传统的SAG模型进行脉冲压缩,也会导致脉冲压缩增益降低和峰值位置偏移,文中给出了定量结果。本文研究表明,在高速运动情况下,SAG模型不再适用,而应该采用本文所给出的IPM模型,尤其对于星载SAR成像处理,按照IPM模型进行一维距离像处理,可得到更清晰的像。
[1]John C C,Robert N M.Synthetic aperture radar system and signal processing[M].New York:Wiley,1991.
[2]Ian G C,Frank H W.Digital signal processing of synthetic aperture radar data:algorithms and Implementation[M].Norwood:Artech House Incorporated,2005.
[3]Xing M D,Wang T.Radar imaging technology[M].Beijing: Publishing House of Electronics Industry,2005.(保铮,邢孟道,王彤.雷达成像技术[M].北京:电子工业出版社,2005.)
[4]Huang H F,Dong Z,Liang D N.Error analysis of“stop and go”hypothesis of spaceborne bistatic SAR[J].Chinese Journal of Radio Science,2006,21(6):863-878.(黄海风,董臻,梁甸农.星载双站SAR“停走停”假设误差分析[J].电波科学学报,2006, 21(6):863-878.)
[5]Geng S M.Research on key technologies of FM_CW synthetic aperture radar signal processing[D].Changsha:National Uni-versity of Defense Technology,2008.(耿淑敏.FM_CWSAR信号处理关键技术研究[D].长沙:国防科学技术大学,2008.)
[6]Qiu X L,Han C Z,Liu J Y.A method for spaceborne SAR geolocation based on continuously moving geometry[J].Journal of Radars,2013,2(1):54-59.(仇晓兰,韩传钊,刘佳音.一种基于持续运动模型的星载SAR几何校正方法[J].雷达学报, 2013,2(1):54-59.)
[7]Chen JJ,Wang S L.Echo model of ultra-high speed moving target and it influence on radar detection[J].Modern Radar,2007,29 (8):60-63.(陈建军,王盛利.超高速运动目标回波及其对雷达检测的影响[J].现代雷达,2007,29(8):60-63.)
[8]Tao R,Zhang N,Wang Y.Analysing and compensating the effects of range and Doppler frequency migrations in linear frequency modulation pulse compression radar[J].IET Radar, Sonar and Navigation,2011,5(1):12 22.
[9]Yang L M,Su W M,Gu H,et al.Application of state-space method to velocity and range profile estimation of moving target for ultra-wide band radar[J].Journal of Electronics&Information Technology,2012,34(5):1051-1056.(杨利民,苏卫民,顾红,等.状态空间法在超宽带雷达动目标速度及距离像估计中的应用[J].电子与信息学报,2012,34(05):1051-1056.)
[10]Yang L M,Su W M,Gu H,et al.Velocity estimation of moving target based on tow-dimensional projection of LFM UWB radar[J].Journal of Radars,2012,1(3):232-237.(杨利民,苏卫民,顾红,等.基于二维映射的LFM UWB雷达动目标速度估计[J].雷达学报,2012,1(3):232- 237.)
廖桂生(1963
徐雪菲(1990-),通信作者,男,教授,博士研究生导师,主要研究方向为雷达信号处理。
E-mail:liaogs@xidian.edu.cn
IPM model for radar echo signal of hypersonic targets
XU Xue-fei,LIAO Gui-sheng
(National Lab of Radar Signal Processing,Xidian University,Xi’an 710071,China)
That stop and go(SAG)model of echo signal currently used in linear frequency modulation (LFM)pulse compression radar is inaccurate to hypersonic targets for overlooking the range variation within single pulse duration,which will cause the offset and broadening of mainlobe and increase sidelobe.A more realistic echo model-inner pulse motion(IPM)is presented.A comparison of pulse compression performance under the two models is made by theoretical analysis and experiment results.We found that the pulse compression gain has an increase of 3dB by using the IPM model compared to the SAG model.
echo model;hypersonic target;inner pulse motion(IPM);pulse compression radar
TN 957
A
10.3969/j.issn.1001-506X.2015.03.10
),女,博士研究生,主要研究方向为高超声速目标探测。
E-mail:iexuxuefei@hotmail.com
网址:www.sys-ele.com
1001-506X(2015)03-0537-07
2014 01 20;
2014 06 12;网络优先出版日期:2014 09 26。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20140926.1558.018.html
国家自然科学基金(61231017)资助课题

