基于混沌随机滤波器的CS-MIMO雷达测量矩阵优化设计
彭珍妮,贲 德,张 弓
(1.南京航空航天大学无人机研究院,江苏南京210016; 2.南京航空航天大学雷达成像与微波光子技术教育部重点实验室,江苏南京210016)
基于混沌随机滤波器的CS-MIMO雷达测量矩阵优化设计
彭珍妮1,2,贲 德2,张 弓2
(1.南京航空航天大学无人机研究院,江苏南京210016; 2.南京航空航天大学雷达成像与微波光子技术教育部重点实验室,江苏南京210016)
提出了一种在压缩感知多输入多输出(compressive sensing-multiple input multiple output,CS-MIMO)雷达中利用混沌非线性系统设计随机滤波器进而实现测量矩阵优化的方法。目前,大部分研究采用高斯随机矩阵作为测量矩阵,这类测量矩阵的局限性是,每次仿真实验产生的矩阵互不相同,雷达系统无法实现在线优化,且其对硬件要求高,实现困难。在CS-MIMO雷达信号模型基础上构造稀疏基,提出了基于随机滤波器结构的测量矩阵设计方法,利用混沌序列构造随机滤波器系数,完成对雷达回波的压缩观测。同时以Gram矩阵逼近对角矩阵为准则对随机滤波等效测量矩阵进行优化,进一步提高雷达系统性能。仿真结果表明所提出的基于混沌随机滤波器的CS-MIMO雷达测量矩阵设计与优化算法能够有效提高波达角(direction of arrival,DOA)估计精度。
压缩感知;多输入多输出雷达;测量矩阵;混沌;随机滤波器
0 引 言
近些年,基于压缩感知理论的多输入多输出(multiple input multiple output,MIMO)雷达系统成为雷达领域的一个研究热点[12]。由文献[3-4]提出的压缩感知(compressive sensing,CS)理论指出,只要信号在某个域是稀疏的,就可以仅利用“压缩观测”后的少量数据将原始信号完整地重构出来,突破了传统的奈奎斯特采样定理对采样频率的限制。在大多数场景中,雷达系统感兴趣的目标相对于整个探测空间是稀疏的,这使得基于CS技术的雷达信号处理获得了广泛研究[5]。CS-MIMO雷达的主要优势是接收端不需要匹配滤波,降低了系统复杂度;接收端的采样率低,参数估计所需数据量少,降低了系统对A/D等硬件的性能要求。
设计一个优秀的测量矩阵实现信号的压缩观测是CS的重要思想[6]。现有的CS研究文献给出了测量矩阵的设计准则:由测量矩阵和稀疏基构成的感知矩阵须满足有限等间距(restricted isometry property,RIP)条件[7]。当感知矩阵满足RIP条件时,任意抽取少于K列组成的子矩阵都满足近似正交性,从而保证两个不同的K稀疏信号不会映射成两个相同的压缩域信号。在MIMO雷达系统中,在给定的场景信息和系统参数下,稀疏基主要由MIMO雷达信号模型决定,因此设计一个易于实现又可控的测量矩阵以降低雷达回波信号在压缩域的互相关性,能够提升CS-MIMO雷达性能。
目前大多数研究文献均采用高斯或伯努利随机矩阵作为测量矩阵[8]。这类矩阵的优点是随机性强,能保证感知矩阵各列间低的互相关性。但也有其自身的不足。如文献[9]所述,对于一个由雷达信号模型决定的特定的稀疏基,高斯随机测量矩阵未必是保证感知矩阵各列相关性充分小的最佳选择。事实上,随机测量矩阵在实际雷达系统中很难实现,且每次产生的矩阵都不相同,难以实时控制满足仿真需要。鉴于高斯随机测量矩阵的这些特点,有学者提出将混沌非线性系统用于CS测量矩阵设计。混沌是非线性系统所独有且广泛存在的一种非周期运动形式,它产生的混沌序列对初始值高度敏感并且具有良好的伪随机性质。文献[10]利用logistic映射产生混沌序列构造测量矩阵,并从数学上证明了该矩阵满足RIP性质。文献[11]研究了利用不同混沌系统设计测量矩阵时的重构精度问题。但CS-MIMO雷达的稀疏基和测量矩阵与普通信号不同,上述方法无法直接用于CS-MIMO雷达。文献[12]开展了一些开拓性研究,提出了利用二维时空混沌产生随机测量矩阵,并在CSMIMO雷达信号模型的基础上提出了基于奇异值分解的测量矩阵优化算法,进一步降低了感知矩阵的各列间的互相关性,提高了雷达系统的重构性能。
根据上述研究现状,本文提出了一种新的测量矩阵的设计方法,利用混沌非线性系统构造随机滤波器实现对雷达回波信号的压缩观测,并在此基础上根据CS-MIMO雷达感知矩阵优化思想,进一步优化其混沌随机滤波等效测量矩阵,使回波信号在压缩域的互相关性进一步降低,提升CS-MIMO雷达恢复场景的精度。
1 CS-MIMO雷达信号模型
假定雷达发射窄带信号,远场目标为点目标,其RCS在一个脉冲周期是不变的,不考虑多普勒效应和杂波[13]。
MIMO雷达系统由Nt个发射天线和Nr个接收天线组成。发射信号和接收信号可分别表示为
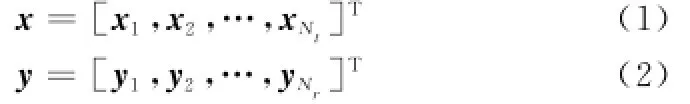
式中,(·)T表示矩阵转置;xi表示通过第i个天线发射的信号;yj表示第j个接受阵元处的信号。
用θ表示某远场点目标的波达角,发射和接收导向矢量可分别表示为

其中,

式中,d表示相邻阵元间距;λ表示载波波长。
那么第j个接受阵元处的接收信号可表示为

式中,βk表示第k个点目标雷达RCS比例系数;ej表示引入的噪声。
将目标角度空间离散化为α=[α1,α2,…,αN],其中N表示离散单元格子的数目,式(5)可以写为

式(6)可进一步写为

式中,Ψj=bjATx,称为稀疏基;s=[s1,s2,…,sN]T。根据CS理论,当远场点目标数远小于N时,目标在角度空间是稀疏的,则s是一个稀疏向量,s中的非零元素表示在这个角度上有目标存在。
通过设计一个q×NrL(q≪NrL,L为一个周期内的快拍数)的测量矩阵Φ,可以得到压缩测量后q×1维的回波数据z:

通过对s的重构估计,即可以获得目标角度信息[14]。
可以看到在具体的CS-MIMO雷达系统中,稀疏基Ψ主要由信号模型确定,因此测量矩阵的设计对重构精度起关键作用。
2 基于Logistic映射的混沌随机滤波器设计
目前大多数研究CS的文献选择高斯矩阵或伯努利随机矩阵为测量矩阵,理论可以证明这类测量矩阵Φ与任意的固定的稀疏基Ψ能够在很大概率上使感知矩阵Θ=ΨΦ满足RIP条件。但是随机测量矩阵对硬件要求极高,在实际雷达系统中很难实现。因此,为了方便对雷达回波信号进行实时测量,本文研究用FIR滤波器结构完成压缩测量[15],如图1所示。CS-MIMO雷达回波信号y(t)首先通过一个低速的A/D转换器,然后通过一个长度为D的随机FIR滤波器,接着对输出信号进行降采样得到测量值z。这种滤波器结构的测量方法具有时不变性,滤波器系数h可预先设计并存储,能够提高应用效率,而且在硬件上比传统的随机测量矩阵容易实现[16]。

图1 基于混沌随机滤波器的信号压缩
如图1所示,随机FIR滤波器的系数采用混沌系统产生而不是用高斯随机变量。这里选用的是研究的比较成熟的Logistic映射,一维Logistic映射数学表达式如下:

式中,xn∈(0,1),表示第n个迭代值;μ是Logistic参数。当3.569 945 6…≤μ≤4时,系统进入混沌状态,迭代产生的值处于一种伪随机分布状态,且μ越接近4,混沌性越强。混沌状态主要表现为两个特点:一是良好的随机性;二是对初始条件的敏感性,即初始条件的微小变化将导致混沌最终状态出现很大差别。本文利用的正是混沌非线性系统的这两个特点:利用其随机性构造随机FIR滤波器系数实现压缩测量,而且只需输入混沌初始条件即可;利用其对初始条件敏感性实现雷达系统的实时在线优化,可以获得与稀疏基较好匹配的测量矩阵,使相应的感知矩阵具有尽可能小的列间互相关性。
在选取滤波器系数时,先让Logistic系统迭代一定的次数后,再靠后选取一段迭代值,以便更好地保证随机性。由压缩测量过程可知混沌随机滤波器对应的等效矩阵是h经逐行移位所得,具有类Toeplitz矩阵的形式。可以从数学上证明该等效测量矩阵与稀疏基构成的感知矩阵能够满足RIP性质[10]。
3 随机滤波等效测量矩阵优化
利用第2节提出的方法产生的等效测量矩阵并未考虑CS-MIMO雷达稀疏基的特点,有必要对其做进一步的优化处理。文献[6]从重构算法性能角度研究了感知矩阵的归一化互相关系数ccΘ,即矩阵各列间归一化互相关系数的绝对值的最大值:

式中,Θi和Θj分别表示Θ的第i列和第j列。感知矩阵互相关系数越小,CS-MIMO雷达系统性能越好。但作为优化准则,依据式(10)难以实施。一个可行的优化方案是研究感知矩阵的Gram矩阵G,G=ΘHΘ,G的对角元素是感知矩阵各列的自相关系数,非对角元素是各列间的互相关系数,因此优化准则可转化为使感知矩阵Θ(Θ=Φ×Ψ)的Gram矩阵G尽可能地逼近对角矩阵,即
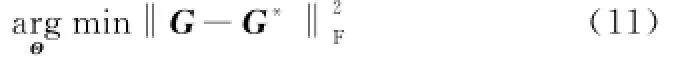
式中,G*=diag(g1,1,g2,2,…,gN,N),是一个对角矩阵,它的对角元素是感知矩阵各列的自相关系数,即gi,i=ΘHiΘi。对角矩阵G*是在理想情况下,感知矩阵具有尽量小的归一化互相关系数时的Gram矩阵。因此,当Gram矩阵G不断逼近对角矩阵G*时,感知矩阵Θ的归一化互相关系数会变小,从而提高信号的恢复精度。
将式(11)作进一步的推导,可以写为

式中,g*=diag(g1,1,g2,2,…,gN,N);Γ是一个半酉矩阵,即ΓHΓ=Ι;c是一个常数。利用奇异值分解对式(12)进行寻优求解,具体步骤如下:
步骤1 根据给定的CS-MIMO雷达发射信号和场景参数构造出稀疏基Ψ;给定Logistic映射的初始值产生混沌序列,得到混沌随机滤波等效测量矩阵Φ,设置迭代终止门限σ。
步骤2 由已知的测量矩阵Φ,计算出半酉矩阵Γ,具体方法是对ΦΨ(g*)-1进行奇异值分解:

其中,Σ是对角矩阵,其对角线上的元素是分解得到的奇异值。可以得到:

步骤3 利用步骤2中计算得到的半酉矩阵Γ,通过下式反解出Φ:

其中,Q=Ψ(g*)-1。注意到Q中存在零元素,最小二乘估计算子无法直接应用。这一问题可以通过奇异值分解后去除为零的奇异值来解决,方法如下:
对Q进行奇异值分解:
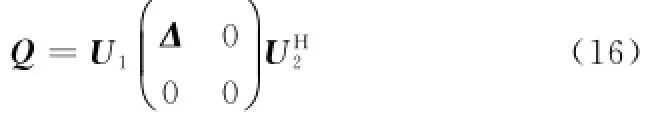
式中,U1和U2为酉矩阵,Δ是由非零的奇异值构成的对角矩阵;Δ=diag(Δ1,Δ2,…,Δq);而q即为Q的奇异值中的非零元素的个数。
步骤4 利用最小二乘估计算子计算出优化的测量矩阵:

需要说明的是,这种寻优算法的本质是基于循环算法的局部优化方法,具有收敛速度快的特点[8]。但由于优化过程中用到了两次奇异值分解,对运算平台的计算能力要求较高。
4 仿真结果与分析
考虑一个CS-MIMO雷达系统,发射阵元数Nt=16,接收阵元数Nr=25,阵元均匀间隔。发射信号为正交Hadamard码,一个周期内的快拍数L=16。假设雷达观测的角度范围为[-25°,25°],压缩后的观测矢量维数M=25。将Logistic映射的初始值设为0.243 2,μ取4,在产生的混沌序列中截取一段构造混沌随机FIR滤波器系数。
4.1 感知矩阵的归一化互相关系数
图2给出的是当CS-MIMO雷达发射波形一定时,分别采用高斯随机测量矩阵、混沌随机滤波器及其优化得到的滤波器所对应的感知矩阵的归一化互相关系数的统计直方图,均以0.025为间隔进行统计。表1给出的是对应图2中的感知矩阵归一化互相关系数的平均值和最大值。由结果可见,高斯随机矩阵与混沌随机滤波器所对应的感知矩阵归一化互相关系数的平均值比较接近,但后者的最大值低于前者,相差0.196 7,由前面理论分析可知,在重构性能方面,混沌随机滤波器要略优于高斯随机矩阵。混沌随机滤波器经优化算法后,感知矩阵归一化互相关系数有明显变化,集中于小于0.4的范围内,其平均值和最大值分别减小了0.035 3和0.135 5,验证了优化算法的有效性。
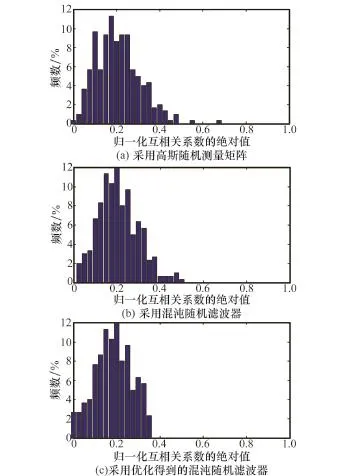
图2 感知矩阵的归一化互相关系数统计直方图
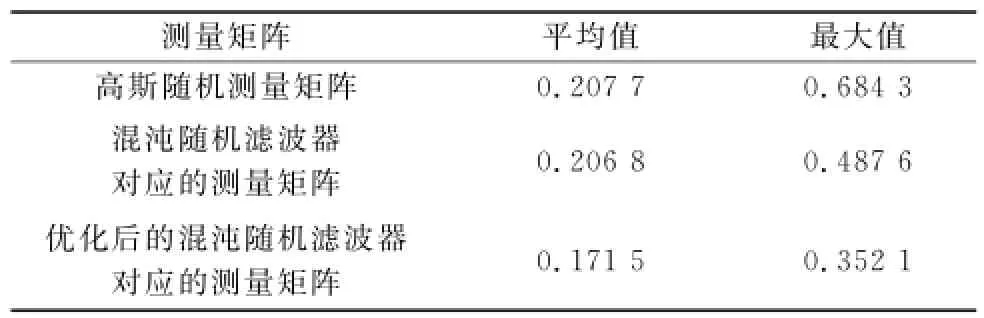
表1 感知矩阵的归一化互相关系数统计表
4.2 滤波器优化前后的DOA估计性能比较
假设远场目标位于[-25°,25°],雷达回波中混有均值为零的高斯白噪声。利用OMP重构算法实现DOA估计:
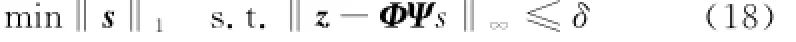
图3给出的是当目标波达角分别为-20°,-12°,-4°, 4°,10°和18°时,采用混沌随机滤波器及其优化后的滤波器的DOA估计结果。可见,利用优化后的混沌随机滤波器能够将6个目标准确地估计出来,而优化前的滤波器最多只能获得4个目标的DOA估计,优化后的滤波器能进一步提升CS-MIMO雷达系统的性能。

图3 DOA估计结果
4.3 蒙特卡罗仿真
利用蒙特卡罗实验来分析不同稀疏度下,即远场目标个数K取不同值时,采用高斯随机测量矩阵、混沌随机滤波器及其优化得到的随机滤波器所对应的系统DOA估计精度。采用均方根误差(root mean square error,RMSE)来描述其估计精度,DOA估计的均方根误差定义为

图4给出的是当其他参数固定时,分别进行1 000次蒙特卡罗仿真实验得到的DOA估计误差随稀疏度(目标个数)的变化曲线。可见,随着目标个数的增大,DOA估计误差逐渐增大。但优化后的滤波器对应的估计误差度始终低于高斯随机矩阵和优化前的混沌随机滤波器;混沌随机滤波器与高斯随机矩阵对应的估计误差比较接近,这与第4.1节中的分析相吻合。
图5给出的是当系统稀疏度K=5,采用优化后的混沌随机滤波器时,进行1 000次蒙特卡罗实验得到的DOA估计误差随Logistic映射初始值x0的变化曲线。可以看出,当x0在(0,1)之间取值时,估计误差出现小幅度浮动,但误差均在可接受的范围之内。出现浮动的原因是,logistic映射对初始值的变化十分敏感,初始值微小的差别,得到的混沌序列差别很大,从而影响随机滤波器的系数,进而影响到估计误差。混沌系统的这一特点可以用于在线优化,只需调整混沌初始值,可获得与雷达稀疏基构成的感知矩阵重构性能较优的随机滤波器系数,这是利用混沌序列设计滤波器系数的一个优势。

图4 不同稀疏度下的DOA估计精度
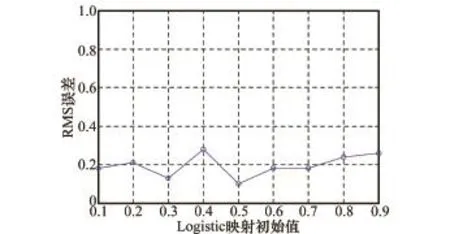
图5 不同混沌初始值下的DOA估计精度
5 结 论
本文提出了一种基于混沌随机滤波器的CS-MIMO雷达测量矩阵优化设计方法。利用随机滤波器设计等效测量矩阵,随机滤波器系数由混沌非线性系统产生,使感知矩阵能够满足RIP特性,避免了采用高斯随机测量矩阵的硬件实现困难问题,利用混沌系统对初始值的敏感性还可以实现系统的在线优化。同时,提出了基于奇异值分解的感知矩阵优化算法,能够有效降低感知矩阵列间相关性,从而降低了雷达目标DOA估计误差,显著提高了CS-MIMO雷达系统性能。仿真实验证明本文提出的测量矩阵优化设计方法是有效可行的。
[1]Ender J H G.A brief review of compressive sensing applied to radar[C]∥Proc.of the 14th International Radar Symposium, 2013:3-16.
[2]Wang H Q,Zhu X H,Li Y S.Parameter estimation for transmit diversity MIMO radar based on distributed compressive sensing[J]. Systems Engineering and Electronics,2012,34(12):2463-2467.(王海青,朱晓华,李彧晟.基于DCS的发射分集MIMO雷达参数估计[J].系统工程与电子技术,2012,34(12):2463 2467.)
[3]Candes E J,Wakin M B.An introduction to compressive sampling[a sensing/sampling paradigm that goes against the common knowledge in data acquisition][J].IEEE Signal Processing Magazine,2008,25(2):21-30.
[4]Candes E J.The restricted isometry property and its implications for compressed sensing[J].Comptes Rendus Methematique, 2008,346(9):589-592.
[5]Ender J H G.On compressive sensing applied to radar[J].Signal Processing,2010,90(5):1402-1414.
[6]Elad M.Optimized projections for compressed sensing[J]. IEEE Trans.on Signal Processing,2007,55(12):5695-5702.
[7]Donoho D.Compressed sensing[J].IEEE Trans.on Information Theory,2006,52(4):1289-1306.
[8]Zhang J D,Zhu D Y,Zhang G.Adaptive compressed sensing radar oriented toward cognitive detection in dynamic sparse target scene[J]. IEEE Trans.on Signal Processing,2012,60(4):1718 1729.
[9]Yu Y,Petropulu A P,Poor H V.Measurement matrix design for compressive sensing-based MIMO radar[J].IEEE Trans. on Signal Processing,2011,59(11):5338-5352.
[10]Yu L,Pierre B J,Zheng G,et al.Compressive sensing with chaotic sequence[J].IEEE Signal Processing Letters,2010, 17(8):731-734.
[11]Kafedziski V,Stojanovski T.Compressive sampling with chaotic dynamical systems[C]∥Proc.of 19th Telecommunications Forum,2011:695-698.
[12]Peng Z N,Zhang G,Zhang J D,et al.Optimized measurement matrix design using spatiotemporal chaos for CS-MIMO radar[J]. Mathematical Problems in Engineering,2014:1-8.
[13]Yang M,Zhang G.Parameter identifiability of monostatic MIMO chaotic radar using compressed sensing[J].Progress in Electromagnetics Research B,2012,44:367-382.
[14]Liu Y,Wu M Y,Wu S J.Fast OMP algorithm for 2Dangle estimation in MIMO radar[J].Electronics Letters,2010,46 (6):444-445.
[15]Tropp J A,Wakin M B,Duarte M F,et al.Random filters for compressive sampling and reconstruction[C]∥Proc.of the IEEE International Conference on Acoustics,Speech and Signal Processing,2006,872-875.
[16]Song L,Cao J H.Radar signal sampling and target reconstruction via random filtering[J].Science&Technology Review, 2008,26(13):64-67.(宋琳,曹吉海.基于随机滤波的雷达信号采样和目标重建方法[J].科技导报,2008,26(13):64- 67.)
Measurement matrix optimization for CS-MIMO radar based on chaotic random filter
PENG Zhen-ni1,2,BEN De2,ZHANG Gong2
(1.Research Institute of UAV,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China; 2.Key Laboratory of Radar Imaging and Microwave Photonics,Ministry of Education, Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
An optimized measurement matrix design method for compressive sensing-multiple input multiple output(CS-MIMO)radar is proposed by applying the chaotic dynamical system to random filter design.Most of the previous research takes the Gaussian random matrix as the measurement matrix.However,it cannot realize on-line optimization and is hard to be implemented in physical electric circuit.Considering that the basis matrix is obtained from the CS-MIMO radar signal model,we propose a new measurement matrix design method applying the random filter.By constructing the filter coefficients with the chaotic sequence,the CSis achieved for the received signal.Moreover,an optimization method is performed on the equivalent measurement matrix of the random filter,by making the Gram matrix approach the diagonal matrix.The simulation results show that the proposed measurement matrix design and optimization method based on the chaotic random filter can effectively improve the direction of arrival(DOA)estimation accuracy of the CS-MIMO radar.
compressive sensing(CS);MIMO radar;measurement matrix;chaos;random filer
TN 958.4
A
10.3969/j.issn.1001-506X.2015.03.09
彭珍妮(1982-),女,助理研究员,博士研究生,主要研究方向为压缩感知雷达、雷达信号处理。
E-mail:pengzhenni@nuaa.edu.cn
贲 德(1938-),男,研究员,博士研究生导师,院士,主要研究方向为雷达系统、雷达信号处理。
E-mail:bende01@sohu.com
张 弓(1964-),男,教授,博士研究生导师,主要研究方向为目标探测与识别、雷达信号处理、压缩感知、图像分析与处理。
E-mail:gzhang@nuaa.edu.cn
网址:www.sys-ele.com
1001-506X(2015)03-0532-05
2014 08 27;
2014 11 14;网络优先出版日期:2015 01 28。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20150128.1006.001.html
国家自然科学基金(61071163,61071164,61201367,61271327,61471191);江苏高校优势学科建设工程资助课题

