弹载双基前视SAR建模及运动/同步误差分析
孟自强,李亚超,胡 奇,武春风,邢孟道,保 铮
(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071; 2.中国三江航天集团,湖北武汉430040)
弹载双基前视SAR建模及运动/同步误差分析
孟自强1,李亚超1,胡 奇2,武春风2,邢孟道1,保 铮1
(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071; 2.中国三江航天集团,湖北武汉430040)
弹载双基前视合成孔径雷达(missile-borne bistatic forward-looking synthetic aperture radar,MBFLSAR)是一种将双基前视SAR成像体制应用于弹载平台的新型SAR成像模式,可实现弹载雷达末端俯冲阶段全程二维成像、自主寻的精确制导。结合MBFL-SAR的运动特点,建立了高动态条件下的回波距离模型,并就多普勒频率和多普勒调频率等参数与常规低速双基平台模式进行了对比分析。在此基础上建立了高动态条件下存在运动误差情形的斜距历程、多普勒频率及多普勒调频率误差模型和同步误差模型,并基于误差对MBFL-SAR成像的影响给出了运动参量的约束条件和同步误差的精度要求。仿真结果验证了误差模型的正确性。
合成孔径雷达;弹载双基前视;特性分析;运动误差;同步误差
0 引 言
导弹处于末端俯冲下降段时,实时获取雷达正前方目标的特征信息对于导弹尤为重要,当导弹打击如舰母战斗群及舰船关重部位、近岸舰船编队等复杂背景目标时,现有单基平台末制导手段中,单脉冲雷达测角、斜前视合成孔径雷达成像等制导方式难以对正前方目标区域进行全程二维高分辨成像探测,因而很难实现对目标的有效分离[12]。弹载双基前视合成孔径雷达(missile-borne bistatic forwardlooking synthetic aperture radar,MBFL-SAR)是将双基前视SAR成像体制应用于弹载平台,发射平台斜视、接收平台前视工作的双基地成像模式。收发平台分置,可为接收机前视成像提供足够的多普勒带宽,从而可实现前视二维较高分辨率成像,弥补了单脉冲雷达测角以及单基地SAR无法对正前方目标二维成像的缺陷[3-4];相对于单基弹载平台,双基前视模式低截获特点和隐身能力可使MBFL-SAR实现弹载末端俯冲下降阶段全程二维成像、自主寻的精确制导,在对地质探测、无人机协同作战、导弹主动寻的等方面具有潜在的体制优势。
在SAR成像研究中,成像机理、成像性能以及信号特性,可从理论上反映场景目标的成像可能性和分辨能力,且与后期成像算法的研究和系统参数的设计密切相关。MBFL-SAR较高速度和加速度的存在会导致该模式下的运动误差相对低速平台更加剧烈;另外,为得到质量良好的聚焦图像,收发平台时间、频率相位同步[5]相对与低速平台应满足不同的精度要求。因此,需要在此研究基础上进行该模式下算法的设计。文献[6-7]针对机载双基地平行等速模式的运动误差及同步问题进行了研究;双基SAR时间和频率同步误差对成像的影响在文献[8-10]中进行了分析;星机双基地SAR系统运动误差分析和同步问题的研究在文献[11-13]中得到了体现。但这些文献均不是专门针对弹载平台的空间几何特点及同步机制进行的研究,因此有必要在这些研究成果的基础上,专门分析研究MBFL-SAR中运动误差和时/频同步误差的特点,以明确该构型下系统误差和同步机制的必要性。
本文针对MBFL-SAR这种特殊的双基前视成像体制,首先从MBFL-SAR几何构型入手,推导了双基距离模型和回波信号模型,并与常规低速双基平台对比,针对高速机动平台下变化剧烈的双基距离历程及多普勒历程进行了讨论;之后就MBFL-SAR中运动误差及时/频同步问题对成像性能的影响进行了详细的论证分析,给出了MBFL-SAR成像构型下的距离历程、多普勒历程、多普勒调频率及同步误差模型,以及完成良好聚焦成像满足的速度及加速度约束条件和同步精度要求,为工程应用和实现提供理论指导。
1 弹载双基前视SAR模型建立及运动参数分析
1.1 空间几何模型
图1为MBFL-SAR俯冲下降段成像几何构型。在该阶段,发射机在与平面yOz成夹角的平面内沿曲线做下降运动,斜视照射成像区域(图中阴影部分),瞬时速度为vt,vt在y'方向和z方向的分量分别记为vty'与vtz;接收机在yOz平面内沿曲线做下降运动,前视接收目标区域回波,其瞬时速度为vr,vr在y方向和z方向的分量分别记为vry与vrz。P(xp,yp,0)为测绘带内的一个点目标,这里假设场景平坦,不存在高度起伏。

图1 弹载双基前视SAR俯冲下降段几何构型
1.2 距离模型及回波信号模型
令tm为慢时间,设tm=0时HR和HT分别为接收机和发射机的高度,此时收、发平台在坐标系x Oy和x'Oy'中的位置分别为R0(0,0,HR)和T0(x't,0,HT)。(0,vry0,vrz0)和(0,vty'0,0,vtz0)为此时速度向量,(0,ary,arz)和(0,aty',atz)为加速度向量。假设在任意tm时刻的接收机在坐标系x Oy中的位置坐标为(0,yr,zr),发射机在坐标系x'Oy'中的位置坐标为(x't,y't,zt),则有

根据坐标系间旋转关系,发射机(x't,y't,zt)在坐标系x Oy中的坐标可表示为

则雷达与目标P(xp,yp,0)之间的瞬时双基斜距表示如下:


其中,式中,(x'p,y'p,0)为点目标(xp,yp,0)在发射机坐标系中的位置;Rrcen和Rtcen分别表示收发机在合成孔径中心时刻的目标斜距。
根据SAR的性质可知,当双基斜距的等效斜距近似误差小于发射信号波长的1/4时,可以认为对成像质量没有影响。对于弹载双基前视SAR,需要采用3次近似才能满足成像质量的要求[14]。因此将双基斜距和按泰勒级数展开为tm的幂级数,保留到三次项:
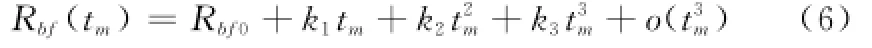
其中

式中,Rbf0表示在合成孔径中心时刻的双基距离和;泰勒级数展开系数k1、k2、k3的值与距离位置Rrcen和Rtcen、运动平台初速度和加速度以及目标的位置有关。
假设弹载SAR发射调频率为γ的线性调频信号,则目标P(xp,yp,0)的基带回波信号可以表示为

式中,wr(^t),wa(tm)分别为雷达线性调频信号的窗函数和方位窗函数;^t为快时间;tm为慢时间;c为光速;λ为波长。
1.3 多普勒参数性能分析
(1)多普勒中心频率
多普勒中心频率表示波束中心线指向点目标时的回波多普勒频率:
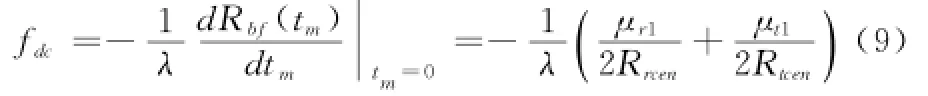
对于常规单基模式下雷达匀速直线运动和双基平行等速模式下收发平台平行且速度相等的情形,多普勒中心频率表现为只与运动参数相关而与目标位置参数无关的参量,位于同一距离单元内所有目标的多普勒中心频率均相同;而对于收发平台不再平行等速的MBFL-SAR,由式(9)可以看出,fdc中与目标位置相关的Rrcen、Rtcen、μr1及μt1会导致不同位置的点目标具有不同的多普勒中心频率,表现为位置的空变性。
(2)多普勒调频率(tm=0时刻)
多普勒调频率为多普勒频率的变化率,可通过对斜距的二次求导得到:

由式(10)可知,相对于常规低速双基SAR,MBFLSAR的多普勒调频率不仅与目标的位置有关,且与收发平台各自运动方向的初速度和加速度密切相关。若不考虑MBFL-SAR的加速度和收发平台高度的变化,则上式退化为常规双基交叉轨道前视SAR多普勒调频率表达式时刻收发平台相对目标的瞬时下视角和斜视角,满足:sinθ1降低为0,收发平台速度相等且均为v,将接收机改为斜视接收,则MBFL-SAR完全转化为双基平行等速斜视模式,此时yp=y'p。因此从某种角度来说,常规双基交叉轨道前视模式和双基平行等速斜视模式可以看成是弹载双基前视模式的一个特殊情况。
,其中θ1和θ2分别表示tm=0
(3)距离走动率
距离走动率(range walk ratio,RWR)表示单位时间点回波的距离走动增量,可以通过双基斜距和展开式的一次项求导得到,即

由式(11)可知,对于不同的点目标具有不同的距离走动率,即弹载双基前视SAR的距离走动具有空变性。利用表1中的仿真参数,对于分别位于(0,8 400,0)和(0,8 600,0)的两个点目标,可计算出在每个方位时刻的距离走动率差异,其中在合成孔径中心时刻其距离走动率相差16.08。距离走动率的空变性导致常规SAR的方位向平移不变特性在弹载双基前视SAR中不再满足,如果在方位时域校正走动量,需要考虑其空变性。

表1 MBFL-SAR仿真实验参数
2 高动态条件下运动误差影响分析
在MBFL-SAR构型下,由于收发平台分置,弹体飞行速度高,运动自由度大,受大气气流扰动和导航飞行控制系统误差的影响,收发机航迹总是与理想轨迹存在一定偏差,运动误差的产生会对该构型下的距离历程、多普勒频率以及多普勒调频率等参数造成影响,且相对于低速机载SAR平台下运动误差的影响更复杂。这里针对高动态条件下运动误差对成像的影响进行分析,并给出满足成像要求的速度和加速度约束条件。
以测绘带内的点目标P(xp,yp,0)为例,在方位tm时刻,理想情况下,发射机和接收机应位于A(x't,y't,zt)和 B(0,yr,zr)处,由于运动误差的影响,设发射机和接收机在各个方向偏离理想航线的位置误差分别为(ΔxT(tm), ΔyT(tm),ΔzT(tm))和(ΔxR(tm),ΔyR(tm),ΔzR(tm)),则发射机和接收机的实际位置分别位于C(x't+ΔxT(tm),y't+ ΔyT(tm),zt+ΔzT(tm))和D(ΔxR(tm),yr+ΔyR(tm),zr+ ΔzR(tm)),故此时发收机到目标之间的距离可分别表示为

以及双基斜距和

对式(14)作如下形式[15]的近似:

其中

由于运动平台运动误差的存在,导致双基距离历程与理想发生偏差,进而导致回波信号相位在方位向引入误差,影响方位向成像性能,下面具体分析运动误差对方位向参数的影响。
根据式(8)所示的信号模型,可以得到存在运动误差情况下的瞬时多普勒频率表示如下:

式中,Δfd(tm)表示由于运动误差产生的多普勒偏移误差,可表示为

式中,ΔvxR(tm)、ΔvyR(tm)及ΔvzR(tm)分别表示接收机在3个方向产生的速度误差;ΔvxT(tm)、ΔvyT(tm)及ΔvzT(tm)分别表示发射机在3个方向产生的速度误差。
瞬时多普勒频率包括两部分:式(17)中等号右边前三项表示弹体理想运动产生的瞬时多普勒频率,等号右边第四项表示弹体的速度误差对双基瞬时多普勒频率的影响,该项由收发平台两部分影响共同组成,如式(18)所示。
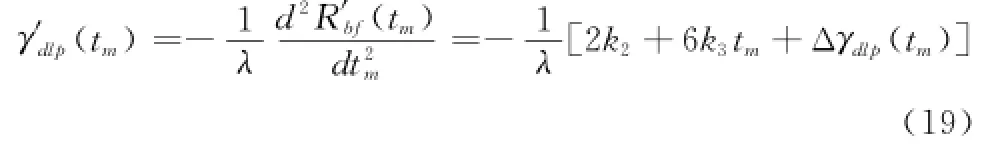
类似可得到存在运动误差情况下的瞬时多普勒调频率,表示如下:式中,Δγdlp(tm)表示由于运动误差产生的多普勒调频率误差,可表示为

式中,ΔaxR(tm)、ΔayR(tm)及ΔazR(tm)分别表示接收机在3个方向产生的加速度误差;ΔaxT(tm)、ΔayT(tm)及ΔazT(tm)分别为发射机在3个方向产生的加速度误差。
回波信号的瞬时多普勒调频率由两部分构成,式(19)中等号右边前两项表现为弹体理想运动产生的方位向信号调制,等号右边第三项表现为弹体的运动加速度误差对多普勒调频率的影响,该项由收发平台两部分影响共同组成,如式(20)所示。
基于以上对运动误差的分析,这里建立弹载双基前视平台下的运动误差模型:

式中,ΔRbf0表示固定误差;Δvbf表示线性误差系数;Δabf表示二次误差系数;h(tm)表示三次及以上误差。
如果受到运动误差ΔRbf(tm)的影响时回波信号(忽略幅度项)变为

对回波信号去载频得到基频信号,并进行距离向傅里叶变换得到:

由式(23)可知,运动误差引入误差相位项exp[-j2π·其中相位项会导致距离向聚焦位置发生偏移,同时在方位向出现误差相位项exp[-j2πfc]。固定误差ΔRbf0会引起距离向产生线性误差相位项e,导致距离向聚焦位置偏移,方位向误差相位项为常数,对成像无影响;线性误差Δvbftm造成方位向线性误差相位项,该项会引起方位向驻相点偏离理想位置,最终导致聚焦位置发生偏移;二次误差0.5Δabf·引入方位向二次误差相位项该项会导致图像在方位向的主瓣展宽和副瓣升高;三次及高次项误差h(tm)会导致方位向图像非对称旁瓣升高。
以上完成了运动误差对成像的影响分析,由于弹载双基前视SAR运动平台的复杂性,在完成良好的图像聚焦之前需要完成高精度的运动补偿。为定量分析运动补偿的要求,导出运动误差参量的补偿精度,下面针对弹载双基前视SAR构型下速度和加速度等运动参量给出具体的约束条件。
由式(16)可知,对于平行等速双基SAR,平台高度zr和zt在运动过程中保持不变,根据yr和y't均是方位时间递增函数的特性可知,在合成孔径边缘时刻的运动误差最大,即ΔRbf(tm)取得最大值;然而,弹载双基前视SAR平台工作在弹体下降段,收发平台的高度时刻变化,导致运动误差不仅与收发平台的水平向位置参数yr、x't及y't有关,而且与运动平台高度向位置参数zr和zt密切相关,故从上式不能直接得知运动误差对应的最大时刻。现根据表1中参数进行仿真,分析运动误差的变化规律。这里针对运动误差分固定误差、线性误差、二次误差和三次及以上误差等不同情形分别进行分析仿真。仿真中采用固定误差为10 m,线性误差系数为5 m/s,二次误差系数为0.5 m/s2,三次及以上误差系数均为0.1,结果如图2所示。
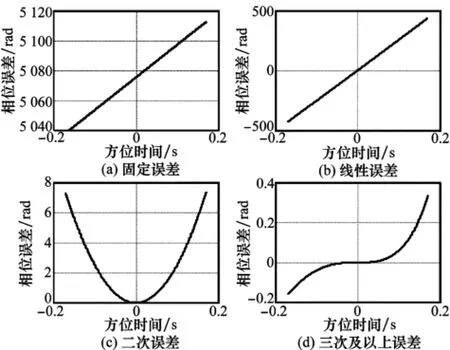
图2 不同情形下运动误差引入的相位误差
由图2可知,在MBFL-SAR构型下,不同运动误差情形导致的运动误差各不相同,但不同情形下运动误差均是在合成孔径边缘时刻达到最大,下面以线性误差不大于π、二次误差不大于π/4为限制条件[16],给出具体速度和加速度的约束条件。
(1)速度误差约束
当收发平台存在固定速度误差时,收发平台运动误差可表示为
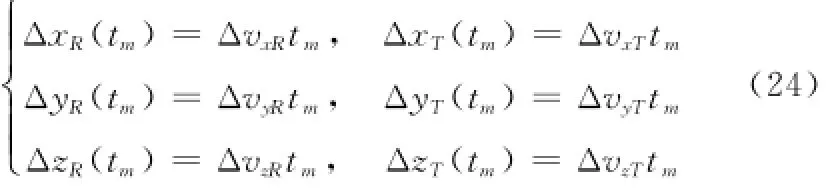
假设收发机各个方向误差量级相同(ΔvxR=ΔvyR= ΔvzR=ΔvR,ΔvxT=ΔvyT=ΔvzT=ΔvT),考虑最不利的误差方向相反的情况(ΔvR=-ΔvT=Δv),且以合成孔径时间内最大相位误差不大于π为限制条件,根据式(16)可得速度的约束条件:

即
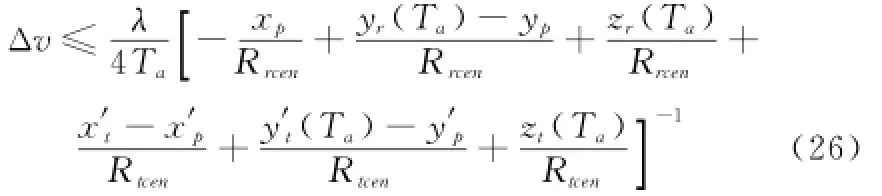
式中,y't(Ta)、zt(Ta)分别表示发射机在合成孔径边缘时刻的位置和高度;yr(Ta)、zr(Ta)分别表示接收机在合成孔径边缘时刻的位置和高度。
(2)加速度误差约束
当收发平台存在固定加速度误差时,收发平台运动误差可表示为

假设收发机各个方向误差量级相同(ΔaxR=ΔayR= ΔazR=ΔaR,ΔaxT=ΔayT=ΔazT=ΔaT),考虑最不利的误差方向相反的情况(ΔaR=-ΔaT=Δa),且以合成孔径时间内最大相位误差不大于π/4,根据式(16)可得加速度的约束条件:

即

对于常规低速机载平台,由于机械惰性较大,沿航向速度变化较慢,即在该方向的加速度误差可以忽略,加之其飞行高度不变,在运动补偿时只需考虑载机侧向运动误差即可,而对于MBFL-SAR,由于其高动态运动特点,机动性较大,运动过程中各个方向变化剧烈,因此运动补偿必须同时考虑3个方向上的运动误差。
3 高动态条件下同步误差影响分析
与运动误差类似,高动态条件下的时间、频率相位同步误差问题也是制约弹载双基前视SAR成像性能的重要问题,由于弹载平台的高机动性,相对于常规低速双基SAR运动平台,同步问题在该成像构型下成像精度要求有所不同,下面分别针对时间、频率相位同步误差问题对MBFLSAR成像性能的影响进行详细的理论分析和仿真研究,并针对该成像模式分别提出了满足成像要求所对应的同步精度要求。
3.1 时间同步误差
时间同步误差是由于发射机和接收机分置,两平台时间基准不同而产生。时间同步误差Δτ(tm)包括3个部分:由两站PRF触发不同步引入的固定时间误差Δτ0、由于两站PRF周期PRI不相等引入的随方位时间变化的线性时间误差以及随机时间误差rand(tm),即

式中,Δτl(tm)=Δ/PRI*tm,表示相邻两个采样窗之间的PRI误差;Δ为相邻回波时间误差;随机时间误差rand(tm)符合均值为0,方差为σ2的正态分布,即
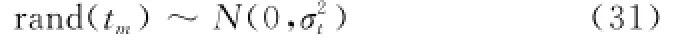
如果受到时间同步误差Δτ(tm)的影响时回波信号(忽略幅度项)变为
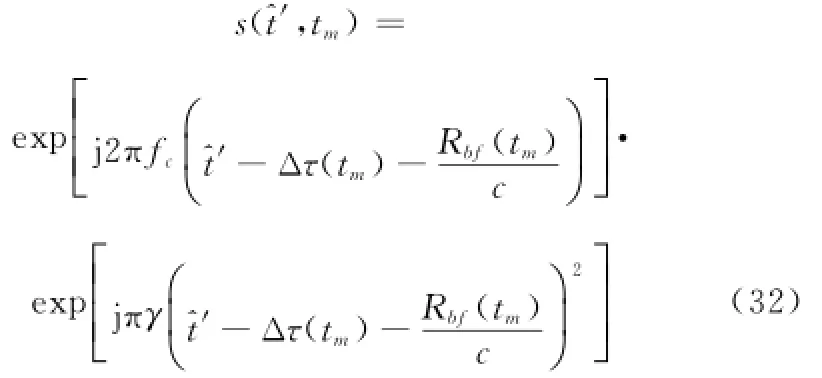
对回波信号去载频得到基频信号,并进行距离向傅里叶变换得到

由式(33)可知,时间同步误差引入线性误差相位项exp[-j2πfrΔτ(tm)],该项会导致距离向聚焦位置发生偏移,同时在方位向出现误差相位项exp[j2πfcΔτ(tm)]。固定时间误差Δτ0引入距离向线性误差相位项exp[-j2πfrΔτ0],引起距离向聚焦位置偏移,导致回波采样窗的偏移,回波采样信号带宽变窄,造成距离分辨率下降,方位向误差相位项exp[j2πfcΔτ0]为常数,对方位向无影响;线性时间误差Δτl(tm)造成距离向线性误差相位项exp[-j2πfrΔτl(tm)],聚焦位置偏移量与方位时间有关,方位向误差相位项为exp[j2πfcΔτl(tm)],该项会导致图像在方位向的主瓣展宽和副瓣升高,相对于机载平台,高速平台下的脉冲重复频率一般较高,意味着在合成孔径时间内方位向所能容忍的相邻回波时间误差更小,即对线性时间误差精度的要求更高;随机时间误差rand(tm)满足正态分布,主要造成图像在方位向副瓣升高,对积分旁瓣比影响较大。
3.2 频率相位同步误差
由于发射机和接收机分别采用独立的频率源,两频率源间任何频率误差及频率不稳定便会导致回波信号的相位误差。频率同步误差Δf(tm)包括3部分:发射载波与接收本振的频率偏差引入的固定频率误差、两频率源不稳定引入的线性频率同步误差以及随机频率误差,即

时间间隔τ内引起的回波相位误差表示如下:
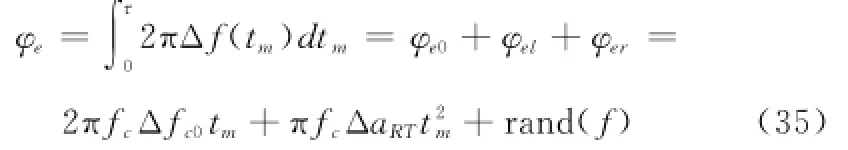
式中,时间间隔τ一般要求至少为一个合成孔径时间,即τ≥Ta,Ta为合成孔径时间。2πfcΔfc0tm为固定频率误差引入的线性误差相位项,该项主要引起聚焦图像在方位向的位置偏移;πfcΔaRTt2m为线性频率误差引入的二次误差相位项,该项主要导致图像在方位向主瓣展宽和副瓣升高; rand(f)表示一个PRI时间内回波信号的相位误差,满足均值为0,方差为σ2f的正态分布。
4 仿真结果及分析
本节通过计算机仿真验证运动误差及同步误差对成像的影响,仿真参数如表1所示,场景中心位于(0,8 500,0),结果如图3~图5所示。
仿真1 高动态条件下运动误差对成像的影响仿真
图3表示各类运动误差对点目标成像影响的仿真结果,图3(a)给出的是固定运动误差ΔRbf0=100 m时的仿真结果,误差的加入引起图像主瓣在距离向偏离理想位置13.56 m,图像质量没有受到误差的影响;图3(b)表示线性运动误差系数Δvbf=5 m/s时的结果,图像聚焦位置在方位向偏移了0.036 2 s,图像质量并无影响;图3(c)给出的是存在二次运动误差系数Δabf=0.6 m/s2时的结果,主瓣宽度由0.531 7 m下降至0.607 6 m,误差的加入同时导致了图像的峰值旁瓣比和积分旁瓣比性能的恶化;三次及以上运动误差引入高次误差相位,导致方位向图像产生主瓣展宽,旁瓣非对称性升高,同时造成图像峰值旁瓣比和积分旁瓣比严重恶化。
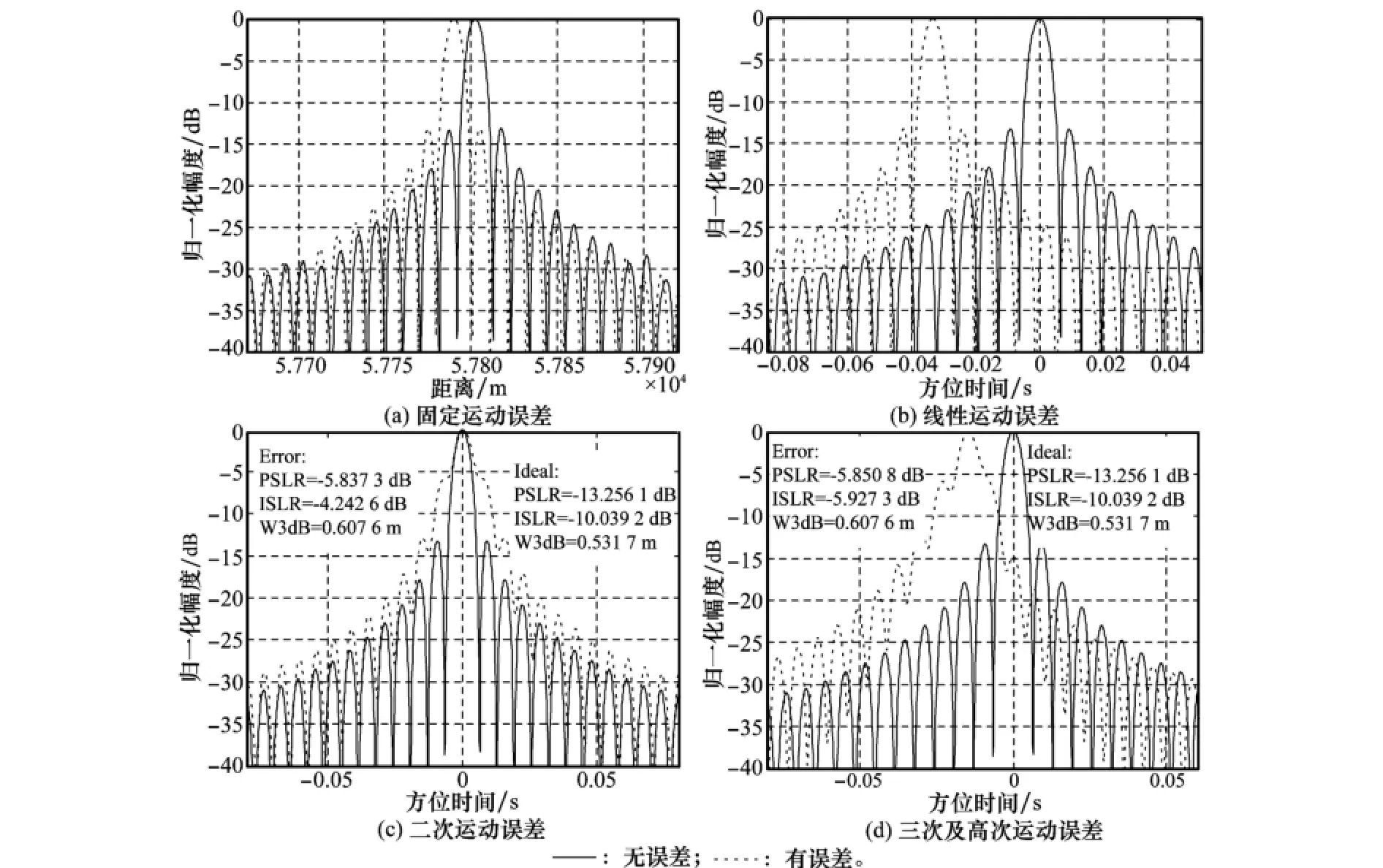
图3 运动误差对成像的影响
仿真2 高动态条件下时间/频率同步误差对成像的影响仿真
利用表1中仿真参数,在高动态条件下分别加入不同类型的时间同步误差和频率同步误差,分别对场景点目标进行成像,分析验证各类同步误差对成像性能的影响,仿真结果如图4所示。图4(a)~图4(c)为时间同步误差对成像影响的仿真结果,其中,图4(a)给出的是固定时间同步误差Δτ0=2×10-6s时的结果,图像主瓣在距离向偏离了60.98 m,同时主瓣宽度由2.625 0 m恶化至5.375 0 m;当相邻回波时间误差Δ=4×10-12s时,线性时间同步误差对成像的影响结果如图4(b)所示,线性时间误差导致图像在方位向偏离理想聚焦点0.049 s,且主瓣宽度、峰值旁瓣比和积分旁瓣比的性能均存在不同程度的下降;图4(c)给出的是正态随机时间同步误差σt=1×10-11时的结果,误差加入前后主瓣位置有所偏移,副瓣升高,导致积分旁瓣比性能下降。图4(d)~图4(f)为频率同步误差对成像影响的仿真结果,其中,图4(d)给出的是当Δfc0=5×10-9时固定频率同步误差对成像影响的结果,图像主瓣在方位向偏离了0.031 s,但图像聚焦质量不受影响;当ΔaRT=1.5×10-9时线性频率同步误差对成像的影响结果如图4(e)所示,线性频率误差导致图像在方位向产生主瓣展宽、旁瓣对称性升高,主瓣宽度由0.531 7 m下降至0.577 3 m,峰值旁瓣比和积分旁瓣比均严重恶化,图像质量严重下降;图4(f)给出的是正态随机频率同步误差σf=5×10-9时的结果,误差加入前后主瓣位置有所偏移,副瓣升高,导致积分旁瓣比性能下降,但主瓣宽度不变,不影响图像分辨率。
由仿真结果可知,对成像性能影响较大的是线性时间同步误差和线性频率同步误差,对于线性时间同步误差,根据多次仿真数据拟合得到图5曲线。由图可知,方位向聚焦误差随着相邻回波时间误差近似成线性增加,为保证成像质量且限制聚焦偏差,要求相邻回波时间误差Δ≤5×10-12s;对于线性频率同步误差,考虑最不利的情况(收发机误差相反且各自误差参数均为Δa),选取相位误差限制条件为:max (φel)=1/2·πfcΔaTa2≤π/4,可求得在合成孔径时间内的频率稳定度为

对于载频fc=15 GHz,合成孔径时间Ta=0.5 s的MBFL-SAR系统,频率稳定度限制要求为ΔaTa≤6.67×10-11。

图4 时间和频率同步误差对成像的影响
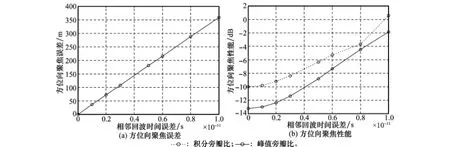
图5 相邻回波时间误差对方位聚焦的影响
5 结 论
作为一种新型的成像模式,弹载双基前视SAR将弹载平台与双基前视成像构型巧妙结合,可弥补单脉冲雷达测角及单基地SAR无法对正前方目标二维成像的缺陷,在对地探测和战场侦察、导弹主动寻的等方面具有潜在的体制优势。与常规低速双基平台不同,高动态条件下MBFL-SAR成像体制中运动平台较高速度和加速度的引入会产生变化剧烈的双基距离历程、多普勒历程,同时运动误差和时/频同步误差问题对高动态条件下的成像带来了困难。本文结合弹体运动特点,建立了高动态条件下MBFL-SAR的运动误差模型和同步误差模型,之后对点目标的仿真验证了模型的正确性,给出的运动参量约束条件和同步精度要求,可为实际工程运动误差补偿和双基时钟同步提供理论依据。
[1]Bi K B,Yang X B,Lu Y H.Missile weapon and guidance technology[M].National Defence Industry Press,2013.(毕开波,杨兴宝,陆永红.导弹武器及其制导技术[M].国防工业出版社,2013.)
[2]Yang L B,Ren X Z,Yang R L.Signal analysis and imaging processing of terminal guidance synthetic aperture radar[J].Systems Engineering and Electronics,2010,32(6):1176 1181. (杨立波,任笑真,杨汝良.末制导合成孔径雷达信号分析及成像处理[J].系统工程与电子技术,2010,32(6):1176 1181.)
[3]Wu J,Huang Y L,Yang J Y,et al.First result of bistatic forward-looking SAR with stationary transmitter[C]∥Proc.of the IEEE International Geoscience and Remote Sensing Symposium,2011:1223-1226.
[4]Espeter T,Walterscheid I,Klare J,et al.Bistatic forward-looking SAR:results of a spaceborne-airborne experiment[J].IEEE Geoscience and Remote Sensing Letters,2011,8(4):765-768.
[5]Tang Z Y,Zhang S R.Bistatic synthetic aperture radar system[M]. Beijing:Science Press,2003.(汤子跃,张守融.双站合成孔径雷达系统原理[M].北京:科学出版社,2003.)
[6]Wang W Q,Liang X D,Ding C B.An Omega-K algorithm with integrated synchronization compensation for bistatic SAR[C]∥Proc.of the International Conference on Radar,2006:1-4.
[7]Tang Z Y,Zhang S R.A study on the system synchronization of a bistatic synthetic aperture radar[J].Modern Radar,2004,26 (1):5-9.(汤子跃,张守融.双站合成孔径雷达系统同步问题研究[J].现代雷达,2004,26(1):5-9.)
[8]Younis M,Metzig R,Krieger G.Performance prediction of a phase synchronization link for bistatic SAR[J].IEEE Geoscience and Remote Sensing Letters,2006,3(3):429-433.
[9]Wang W Q,Ding C B,Liang X D.Time and phase synchronisation via direct-path signal for bistatic synthetic aperture radar systems[J].IET Radar,Sonar and Navigation,2008,2(1):1-11. [10]Zhang X L,Li H B,Wang J G.The analysis of time synchronization error in bistatic SAR system[C]∥Proc.of the IEEE International Geoscience and Remote Sensing Symposium,2005: 4619-4622.
[11]Lei L,Zhou Y Q,Li J W,et al.Synchronization of geo spaceborne-airborne bistatic SAR[C]∥Proc.of the IEEE International Geoscience and Remote Sensing Symposium,2008:1209 -1211.
[12]Saini R,Zuo R,Cherniakov M.Problem of signal synchronisation in space-surface bistatic synthetic aperture radar based on global navigation satellite emissions-experimental results[J]. IET Radar,Sonar and Navigation,2010,4(1):110-125.
[13]Xia M,Yang X N.Motion error analysis of spaceborne-airborne bistatic SAR-GMTI[J].Systems Engineering and Electronics,2012,34(5):925-930.(夏猛,杨小牛.星机双基地SAR-GMTI中的运动误差分析[J].系统工程与电子技术, 2012,34(5):925-930.)
[14]Cumming I G,Wong F H.Digital processing of synthetic aperture radar data:algorithms and implementation[M].Norwood:Artech House,2005.
[15]Xing M D,Jiang X W,Wu R B,et al.Motion compensation for UAV SAR based on raw radar data[J].IEEE Trans.on Geoscience and Remote Sensing,2009,47(8):2870 2883.
[16]Walter G C,Ron S G,Majewski R M.Spotlight-mode synthetic aperture radar[M]:Signal Processing Algorithms,Norwood,MA:Artech House,1995:203- 242.
Modeling and motion/synchronization error analysis of MBFL-SAR
MENG Zi-qiang1,LI Ya-chao1,HU Qi2,WU Chun-feng2,XING Meng-dao1,BAO Zheng1
(1.National Lab of Radar Signal Processing,Xidian University,Xi’an 710071,China; 2.China San Jiang Space Group,Wuhan 430040,China)
Missile-borne bistatic forward-looking synthetic aperture radar(MBFL-SAR)is a new and special imaging mode,which is the application of bistatic forward-looking synthetic aperture radar to the missile platform.It could perform two-dimensional(2D)imaging and passive homing during the whole terminal diving period of the missile.This paper establishes the echo slant range model under high dynamic conditions according to the moving feature of MBFL-SAR.And then motion parameters such as the Doppler frequency and the Doppler chirp rate are analyzed compared with the traditional bistatic platform with low velocities.Furthermore,error models of the slant range history,the Doppler frequency,the Doppler chirp rate and synchronization in the presence of motion errors are built.And restrictions of motion parameters and precision requirements of synchronization errors are developed based on the influence of errors on imaging performance of MBFL-SAR. Simulation results show the validity of the proposed error models.
synthetic aperture radar(SAR);missile-borne bistatic forward-looking;property analysis; motion error;synchronization error
TN 957
A
10.3969/j.issn.1001-506X.2015.03.08
孟自强(1988-),男,博士研究生,主要研究方向为双基前视SAR成像。
E-mail:mengziqiang@hotmail.com
李亚超(1981-),男,副教授,博士,主要研究方向为雷达成像和实时信号处理。
E-mail:ycli@mail.xidian.edu.cn
胡 奇(1986-),男,工程师,硕士,主要研究方向为微波前端设计。E-mail:32698328@qq.com
武春风(1975-),男,研究员,博士,主要研究方向为导弹精确制导。E-mail:252202631@qq.com
邢孟道(1975-),男,教授,博士,主要研究方向为雷达成像和目标识别。
E-mail:xmd@xidian.edu.cn
保 铮(1927-),男,教授,院士,主要研究方向为数字信号处理、阵列信号处理、自适应信号处理和雷达成像。
E-mail:piaofei8@gmail.com
网址:www.sys-ele.com
1001-506X(2015)03-0523-09
2014 26。
网络优先出版地址:http:∥w ww.cnki.net/kcms/detail/11.2422.TN.20140926.1559.019.html
国家自然科学基金(61001211,61303035);中央高校基本科研业务费专项资金(K5051202016)资助课题
05 15;
2014 06 16;网络优先出版日期:2014 09

