考虑反弹行为的单纤维过滤稳态捕集效率的数值模拟

冯 丰，付海明，雷陈磊，张 杰，赵洪亮，朱 辉

（东华大学 环境科学与工程学院，上海 201620）

考虑反弹行为的单纤维过滤稳态捕集效率的数值模拟

冯 丰，付海明，雷陈磊，张 杰，赵洪亮，朱 辉

（东华大学 环境科学与工程学院，上海 201620）

采用稳态单纤维表面粉尘树枝生长随机模拟，并考虑纤维过滤中气溶胶粒子碰撞反弹行为，讨论稳态下斯托克斯数（St）与哈梅克常数（H）对粒子运动轨迹的影响，计算分析了St与H对稳态单纤维捕集效率的影响.研究结果表明：当H值一定时，考虑反弹的捕集效率与不考虑反弹的捕集效率可以按斯托克斯数临界值Stc为分界点写成分段函数，通常1.0≤Stc≤3.5，在St≤Stc的阶段，考虑反弹的捕集效率与不考虑反弹的捕集效率相等，且与文献研究结果基本吻合；在St＞Stc阶段，考虑反弹的捕集效率小于不考虑反弹的捕集效率，需对文献研究结果进行修正，修正结果为文献研究结果乘以反弹系数k，k是St、拦截系数Rp、填充率c及H的函数.

纤维过滤；粒子反弹；捕集效率；数值模拟

随着工业的迅猛发展，空气污染日益严重，大量微粒尤其是气溶胶粒子（指悬浮在空气中的固体或液体粒子物）对人类生存环境和健康产生了严重的威胁.目前，解决空气质量问题最有效的方法之一是空气过滤［1］.国内外已有学者在不考虑粒子碰撞反弹作用条件下，对纤维介质的过滤性能进行了详细的实验及数值研究［2-4］，而实际过滤过程中，通常存在反弹作用，其作用大小与纤维材料相关，文献中单纤维捕集效率的计算结果往往高于实际的捕集效率.目前，考虑粒子碰撞反弹作用的研究报道较少.

本文使用随机模拟方法，考虑粒子碰撞反弹后的运动特性，对纤维表面的反弹行为进行数值模拟，并在考虑反弹作用情况下，研究单纤维捕集效率与斯托克斯数（St）及哈梅克常数（H）的函数关系.

1 数学模型

1.1 Kuwabara模型

Kuwabara单纤维模型［5］用于分析纤维过滤介质表面尘粒捕集问题，其流场示意图如图1所示.由图1可知，圆柱单纤维垂直气流方向置于Kuwabara流场单元的中心，控制面随机产生的粉尘粒子在流动阻力作用下向纤维运动.粒子以速度U进入流场，其径向速度分量为U r，法向速度分量为Uθ.

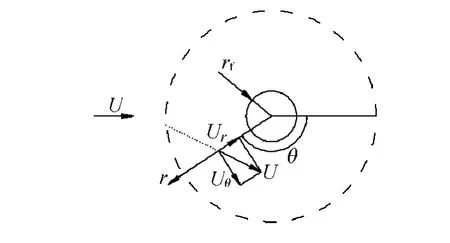
图1 Kuwabara流场单元模型Fig.1 Model of Kuwabara flow cell

Kuwabara流场的边界条件：在纤维表面上速度等于零，在流场边缘处的旋度等于零，径向速度为Ucosθ.引入下列无量纲参量：

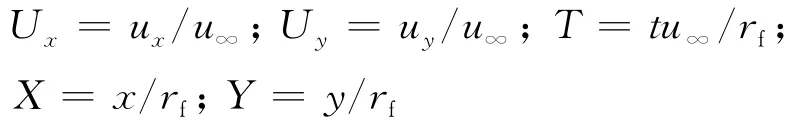
则在图1所示直角坐标系下粒子运动方程为

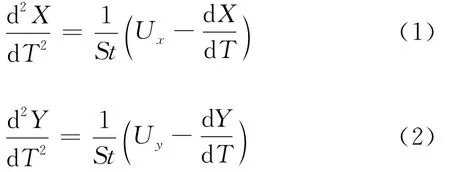
其中：St为表征粒子惯性的斯托克斯数；rf为纤维半径，m；u∞为主流平均速度（即过滤风速），m／s；u x和u y为气流绕纤维流动速度分量，m／s.

在图1所示的直角坐标下，Kuwabara流场速度在x轴和y轴方向分量按式（3）计算

式中：ψ为流函数，m2／s，其解为

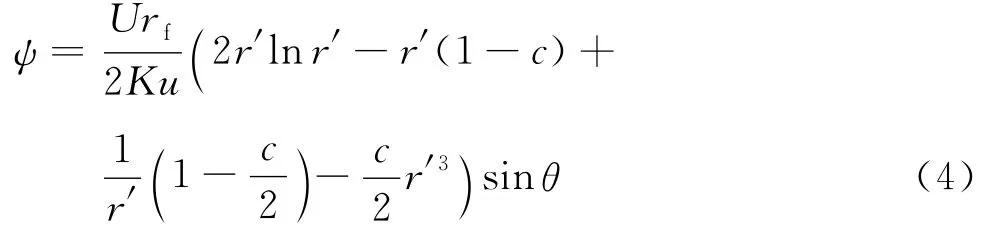
其中：U为气流的参照速度，m／s，U＝U0／（1-c），U0为未受干扰的流体速度，c为填充率；r′＝r／rf，r′为无量纲径向坐标；Ku为Kuwabara动力学因子，由式（5）确定

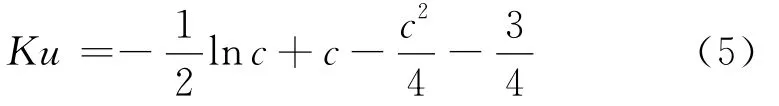
对给定的初始速度和位置，采用四阶Rung-Kutta方法对式（1）和（2）数值积分获得粒子的运动轨迹［6-7］.

1.2 粒子碰撞反弹模型

本文采用 Dahneke［8-10］碰撞反弹理论分析纤维过滤中粒子碰撞反弹行为，其模型如图2所示.

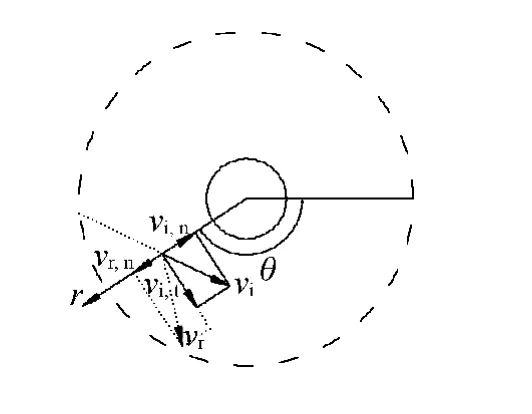
图2 捕集体表面粒子碰撞反弹模型Fig.2 Model of particle impact and rebound on collector surface

输送粒子以速度vi与纤维或已沉积粒子发生碰撞，其法向碰撞速度分量为vi，n，切向碰撞速度分量为vi，t；粒子反弹速度为vr，法向反弹速度分量为vr，n，切向反弹速度分量为vr，t.根据能量守恒原理，粒子碰撞前后的能量守恒方程式为

式中：Ek，in为粒子沿法向的碰撞动能；Ek，rn为粒子沿法向的反弹动能；Ep，i和Ep，r分别为粒子碰撞前后的动力学势能；e为碰撞弹性恢复系数.由式（6）可知，粒子被捕集的条件为反弹动能Ek，rn＝0，假设Ep，i＝Ep，r＝Ew，则粒子反弹临界速度vcr表示为

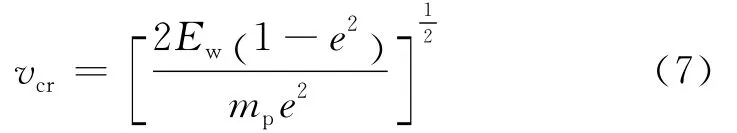
式中：mp为粒子质量，kg.若粒子碰撞法向速度vi，n＞vcr，则粒子发生反弹；反之，粒子被捕集.

1.3 单纤维捕集效率

单纤维捕集效率通常分为稳态捕集效率及非稳态捕集效率.当不考虑已沉积颗粒对捕集效率的影响时，为稳态捕集效率；当考虑随过滤时间的增加，已沉积颗粒成为新的捕集体，使捕集效率随沉积量变化时，为非稳态捕集效率［11-12］.

本文对过滤初期稳态捕集效率进行研究，此时不考虑已沉积粒子对随后来流粒子沉积的影响，仅由纤维体本身对粒子进行捕集，采用基于极限轨迹的单纤维捕集效率计算方法.令t时间内通过控制面的粒子数为N，其中被捕集的粒子数为N0，则稳态单纤维捕集效率η的计算式可表示为

2 结果与分析

本文讨论粒子直径dp＞0.5μm的情形，并忽略其他外力场作用，因此，粒子捕集机制为拦截效应和惯性碰撞.H为表征物质之间范德华吸引能大小的参数.选取不同H作为影响粒子碰撞反弹作用的综合参量，H越小，意味着粒子的黏附能越小，与捕集体碰撞后越容易发生反弹作用.H＝∞表示非反弹碰撞，即粒子一旦与沉积粒子或纤维发生碰撞，粒子就被捕集.纤维长度取Lf＝50μm.

由于气流中粒子分布的随机特征，每次模拟结果为一次随机事件，因此，在相同计算条件下执行多次模拟结果的平均才具有统计意义.稳态单纤维捕集效率随取平均值的数据组数的增加而变化的趋势如图3所示，其中，纵坐标为多次重复模拟计算效率的平均值η，Rp为拦截系数.由图3可知，在模拟次数为25次之后的捕集效率平均值已趋于稳定，因此，在本文的计算中，每种计算条件下执行30次重复模拟，然后对计算结果取平均值.

不同St值下粒子反弹作用对输送粒子运动轨迹的影响如图4所示.模拟计算中所需参数如下：H＝1×10-19J，纤维直径df＝10μm，dp＝1μm，粒子密度ρp＝1 g／cm3，c＝0.05，vi＝0.1 m／s.由图4可知，当St值比较小时，粒子仍按照原有运动轨迹运动，例如St＝0.1时粒子与纤维碰撞后几乎没有反弹；随着St值的增大，粒子运动轨迹发生了明显的变化，与纤维碰撞后的反弹越来越剧烈，导致纤维背风处的“遮蔽区”越来越大，更多的粒子反弹后即逃逸，造成纤维捕集效率降低，例如St值从1.0增大到4.0时，粒子与纤维碰撞后被反弹的部分也随之增加，造成被捕集的粒子越来越少，捕集效率越来越低.

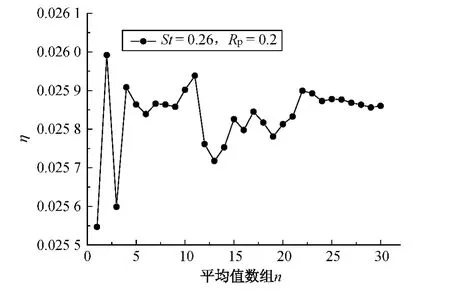
图3 捕集效率平均值随数据组数增大而变化的趋势图Fig.3 The average of collection efficiency with the increase of the number of data sets

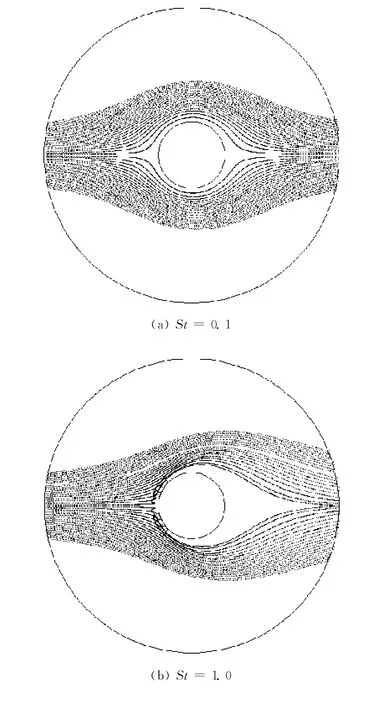
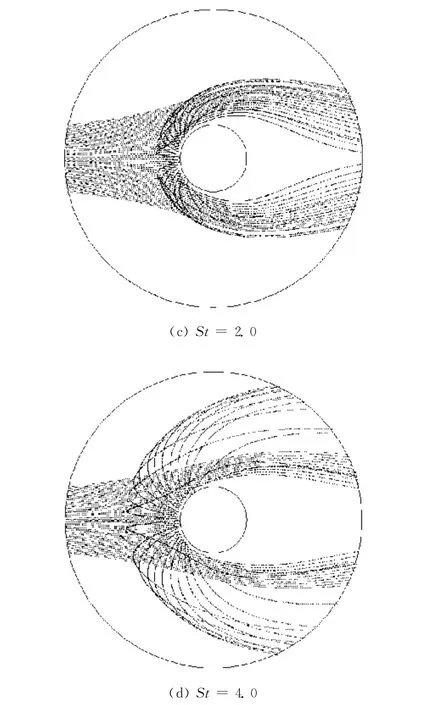
图4 St值对粒子运动轨迹的影响Fig.4 Effect of Stokes number on particle trajectories

不同H值下粒子反弹作用对输送粒子运动轨迹的影响如图5所示.模拟计算中所需参数如下：df＝10μm，dp＝2μm，ρp＝1 g／cm3，c＝0.05，vi＝1 m／s.由图5可知，当H值很小时，粒子与纤维碰撞后几乎都被反弹；随着H值越来越大，粒子与纤维碰撞后反弹的频率越来越小，反弹效果越来越弱；当H值足够大时，粒子与纤维碰撞后几乎不再被反弹.

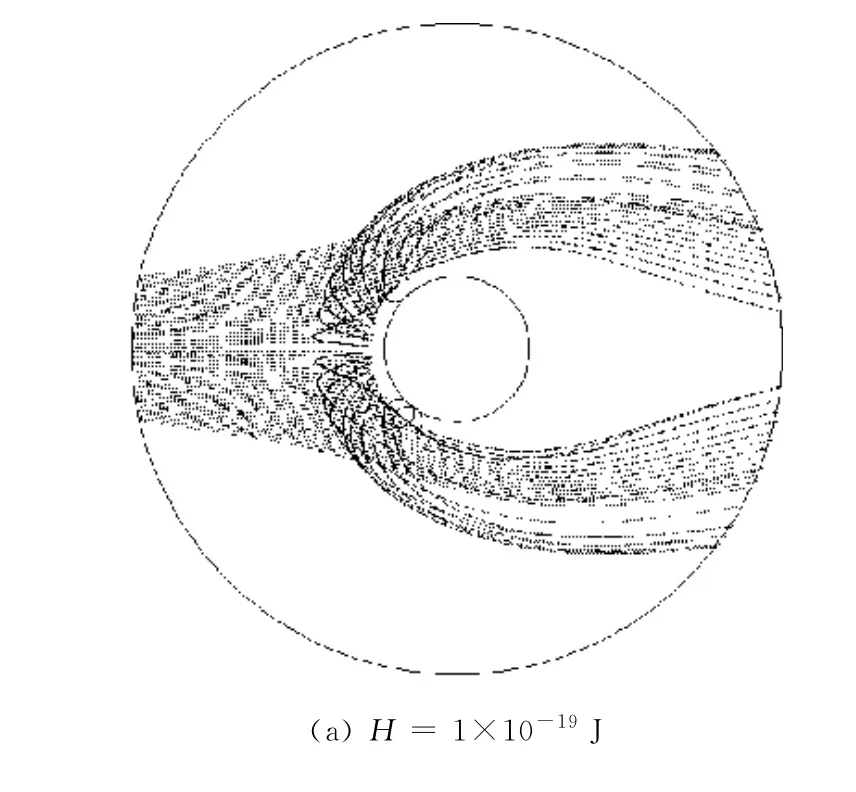
图5 H值对粒子运动轨迹的影响Fig.5 Effect of H on particle trajectories

不考虑反弹时捕集效率模拟数据与经验公式计算结果的对比如图6所示，其中的模拟数据线为误差图表示方式，上下点分别为模拟计算中该组捕集效率值中的最大值与最小值.模拟计算中所需参数如下：df＝10μm，dp＝1μm，ρp＝1 g／cm3，c＝0.05.

图6 无反弹捕集效率的模拟结果与实验研究比较Fig.6 Comparison of collection efficiency between simulated collection efficiency and experimental results without rebounding

由图6可知，捕集效率模拟数据与Davies修正公式及Torgeson公式［13］的计算结果和变化趋势基本一致，两个公式的部分计算结果也在模拟数据的最大值与最小值范围内.随着St值的增大，捕集效率η整体递增，这说明稳态情况或非稳态情况下的颗粒沉积初始阶段，St值对颗粒的捕集起着决定性的作用，这与经典纤维过滤理论的结论吻合［13］.图6中Torgeson公式为

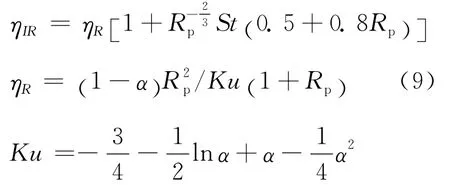
Davies公式为

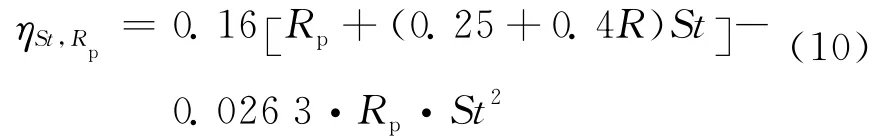
考虑填充率的修正公式为

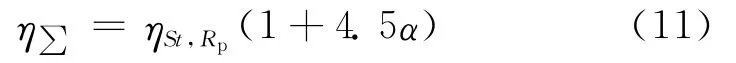
不同H值下St对单纤维捕集效率的影响如图7所示.模拟计算中所需参数如下：df＝10μm，ρp＝1 g／cm3.由图7可知，在St值较小时，St对反弹影响很小，几条反弹曲线基本重合，与不考虑反弹时的效率变化曲线接近一致，捕集效率都随着St值的增大而增大.当St值大于某一个临界值以后，St对于反弹的影响开始变得很显著.不考虑反弹时，捕集效率曲线仍旧随着St的增大而增大；考虑反弹时，在St值大于该临界值的区域捕集效率有一个骤降，之后捕集效率的减小速度开始变慢，最终趋向于一个稳定值.这是因为St值大于反弹临界值的粒子具有较大惯性，与纤维表面发生碰撞频率较高，碰撞后发生反弹的频率也较高，所以造成捕集效率骤降.由于反弹频率有一个上限，不能无限制增长，所以最终捕集效率趋向稳定值，而St值小于反弹临界值的粒子惯性较小，与纤维碰撞的频率较低，捕集效率仍然会提高.此外，当St大于临界值且H比较小时，捕集效率比较低，当H变大时，捕集效率也相应变高，且H越大，该St的临界值越大.当Rp＝0.1，c＝0.05时，临界Stc范围为1.0≤Stc≤1.5；当Rp＝0.5，c＝0.15时，Stc范围为1.0≤Stc≤3.5.

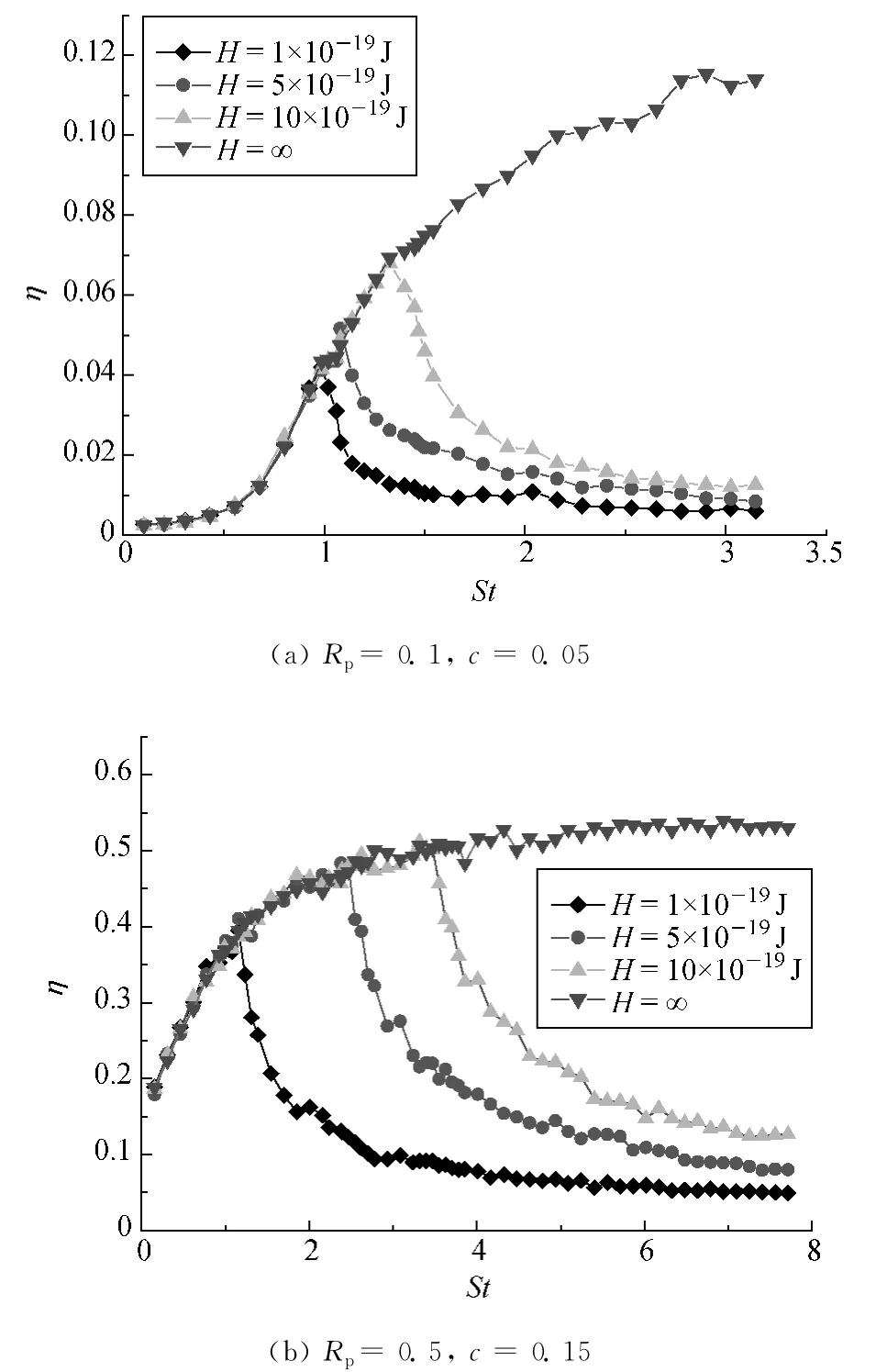
图7 不同H值下St对单纤维捕集效率的影响Fig.7 Effect of Stokes number on collection efficiency in different H

不同H值下反弹捕集效率／无反弹捕集效率与St之间的关系如图8所示.由图8可知，当St≤Stc时，考虑反弹的捕集效率（η反）与不考虑反弹的捕集效率（η0）变化一致；当St＞Stc时，η反／η0随St值变大而减小，关系图像近似为反比例函数图象.将此两种关系写成表达式，有

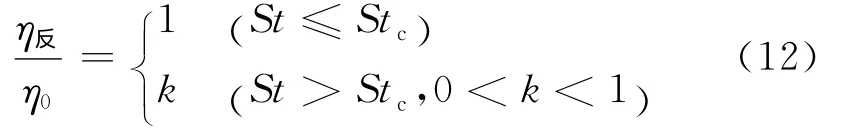
式中：k＝f（St，Rp，c，H），在Rp和c一定的情况下，H值越大时，k值越大，Stc也越大.式（12）说明，在以往的过滤研究中，忽略粒子反弹作用是不准确的，考虑粒子反弹作用与否与该捕集过程的Stc有关，而Stc与Rp，c，H的关系，以及k与Stc，Rp，c，H的关系，需要进一步深入研究.

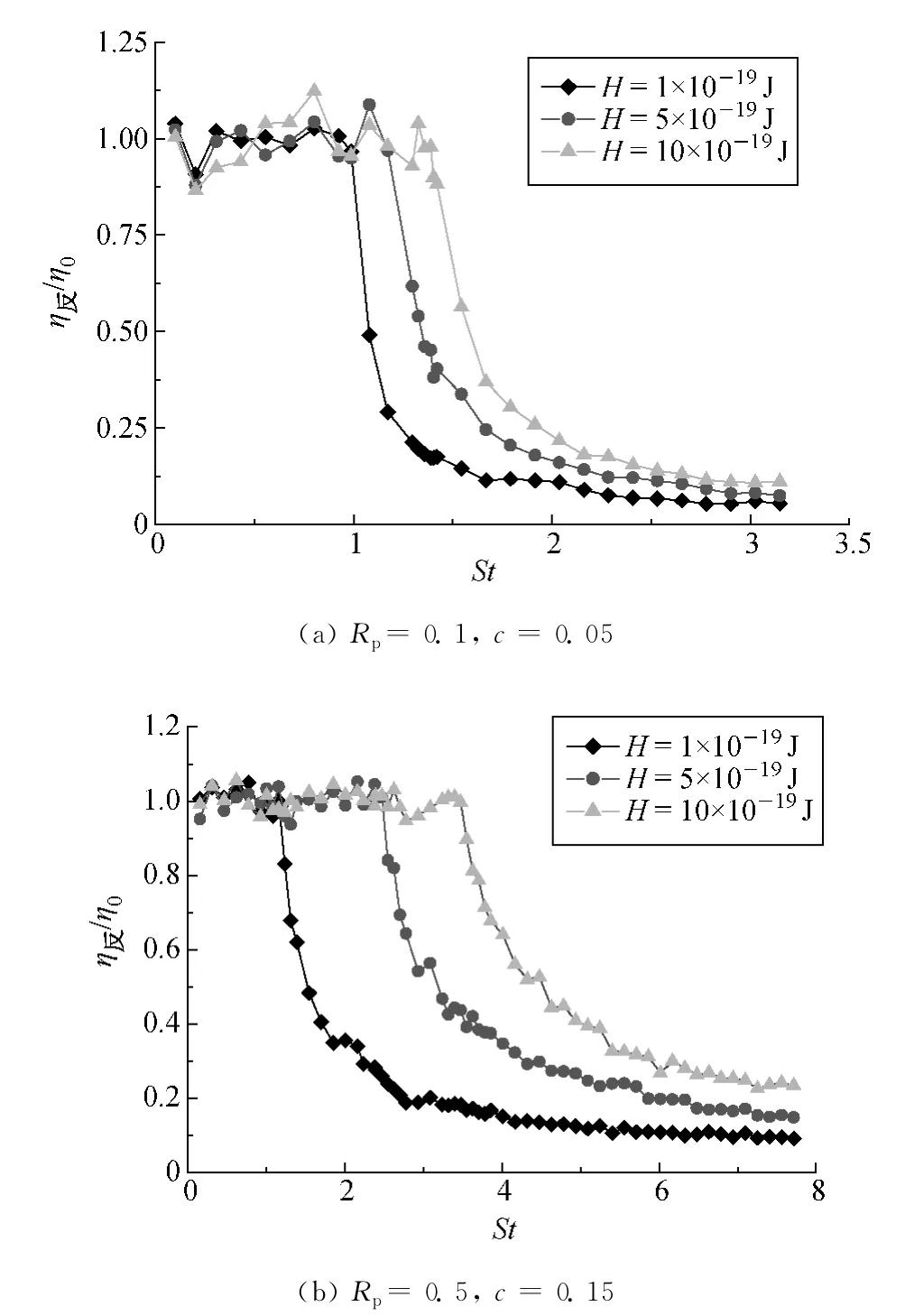
图8 η反／η0与St的关系Fig.8 Relationship betweenη反／η0 and Stokes number

3 结 语

（1）本文采用计算机模拟的方法，对考虑粒子反弹作用下稳态单纤维过滤介质表面粒子的沉积进行了模拟，观察粒子在不同斯托克斯数St时和不同H值时的运动轨迹.由粒子运动轨迹可以看出，在H一定时，St值越大，反弹越剧烈；在St一定时，H值越小，反弹越剧烈.

（2）对数值模拟结果进行分析，随着St值的增大，考虑反弹与不考虑反弹的捕集效率变化在初始基本一致，到某一个St临界值之后（通常1≤Stc≤3.5），考虑反弹的捕集效率均低于不考虑反弹时的捕集效率.这是由于St较大的粒子具有较大惯性，与纤维表面发生碰撞频率较高，碰撞后发生反弹的频率也较高，较小粒径粒子与纤维碰撞的频率较低.

（3）不考虑反弹行为时，模拟结果与文献研究结果基本吻合.在Rp和c一定的情况下，当H值一定时，考虑反弹的捕集效率与不考虑反弹的捕集效率可以按St临界值为分界点写成分段函数，在St≤Stc阶段，两者相等，且等于文献研究结果；在St＞Stc阶段，考虑反弹的捕集效率小于不考虑反弹的捕集效率，需对文献研究结果进行修正，修正结果为文献研究结果乘以反弹系数k，k是斯托克斯数St、拦截系数Rp、填充率c及哈梅克常数H的函数，在Rp和c一定的情况下，H值越大时，k值越大，St的临界值也越大.

［1］付海明，沈恒根.纤维过滤器过滤理论的研究进展［J］.中国粉体技术，2003，9（1）：41-46.

［2］CAI J.Some remarks on efficiency due to dendrite formation［J］.Journal of Aerosol Science，1989，20（8）：959-962.

［3］THOMAS D，PENICOT P，CONTAL P，et al.Clogging of fibrous filters by solid aerosol particles experimental and modeling study［J］.Journal of Aerosol Science，2001，56（11）：3549-3561.

［4］SONG C B，PARK H S，LEE K W.Experimental study of filter clogging with monodisperse PSL particles［J］.Powder Technology，2006，163（3）：152-159.

［5］KUWABARA S. The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers［J］.Journal of the Physical Society of Japan，1959，14（4）：527-532.

［6］朱辉，付海明，亢燕铭.单纤维过滤介质表面尘粒捕集的随机模拟［J］.环境工程学报，2010，4（8）：1881-1886.

［7］朱辉，付海明，亢燕铭.纤维表面气溶胶粒子沉积与反弹行为数值模拟［J］.中南大学学报：自然科学版，2013，44（7）：3086-3094.

［8］DAHNEKE B.The capture of aerosol particles by surfaces［J］.Journal of Colloid and Interface Science，1971，37（2）：342-353.

［9］DAHNEKE B.The influence of flattening on the adhesion of particles［J］.Journal of Colloid and Interface Science，1972，40（1）：1-13.

［10］DAHNEKE B.Measurements of bouncing of small latex spheres［J］.Journal of Colloid and Interface Science，1973，45（3）：584-590.

［11］FU H M.Simulation and prediction on pressure drop during fibrous filters clogged by microbiology particles［J］.Journal of Investigative Medicine，2013，61（4）：S24.

［12］FU H M.3D model for predicting pressure drop and permeability in fibrous porous media ［J］.Journal of Investigative Medicine，2013，61（4）：S22.

［13］DAVIES C N.Air filtration［M］.New York：Academic Press Inc，1973.

Numerical Simulation of Stationary Collection Efficiency of a Single Fiber Filtration Considering the Rebounding Behavior

FENGFeng，FUHai-ming，LEIChen-lei，ZH ANGJie，ZHAOHong-liang，ZHUHui

（School of Environmental Science and Engineering，Donghua University，Shanghai 201620，China）

By using stochastic simulation technique in the growing process of particle dendrites on a single fiber and considering the behavior of aerosol particles collision，adhesion and rebound on surface of fibers，the effects of Stokes number（St）and Hamake constant（H）on particle trajectories in steady state were investigated.The effects ofStandHon stationary collection ef ficiency of a single fiber were examined.The results show that whenHis a fixed value，the relationship between rebounding collection efficiency and no-rebounding collection efficiency can be written as a piecewise function which the demarcation point isStc，these two are equal in the stage of the value ofStis less than or equal toStc，and the findings are consistent with the literature；whenStis greater thanStc，rebounding collection efficiency is less than no-rebounding collection efficiency，the research results are revised，multiplied by rebounding coef ficientk，kis a function ofSt，intercept coefficientRp，filling rateCandH.

fiber filtration；particles bounce；collection efficiency；numerical simulation

TQ 021；TU 834；X 701.2

A

2014-04-25

国家自然科学基金资助项目（51178094；41371445）

冯 丰（1990—），男，陕西宝鸡人，硕士研究生，研究方向为建筑环境空气质量控制.E-mail：fengfengbj0917＠163.com

付海明（联系人），男，高级工程师，E-mail：fhm＠dhu.edu.cn

1671-0444（2015）05-0682-07