斜齿轮传动过程的力学性能及疲劳寿命预测

蒿丽萍

摘 要：根据齿轮传动中轮齿折断和齿面点烛疲劳破坏现象，基于齿轮啮合原理，对斜齿轮啮合过程的力学性能及疲劳寿命预测进行研究，结合实例分析计算齿轮传动过程中齿面接触应力变化规律和齿根弯曲应力变化规律；利用ANSYS建立斜齿轮副有限元模型，分析齿面接触应力和齿根弯曲应力，将其与理论计算结果比较，验证有限元分析方法的正确性；利用FE-SAFE中的名义应力分析法对斜齿轮副的危险部位进行疲劳寿命预测。

关键词：力学性能 疲劳寿命 接触应力 弯曲应力

中图分类号：TG61 文献标识码：A 文章编号：1674-098X（2015）03（b）-0019-04

斜齿轮传动是利用两齿轮轮齿相互啮合传递动力和运动的传动机构，具有承载能力高、传动平稳、传动效率高等特点，广泛应用于机械工程传动装置中。由于齿轮传动过程中承受循环载荷作用，经过一定循环次数后齿轮将产生疲劳裂纹，最终发生断裂，也就是疲劳失效[1]。据在关统计，机械故障中齿轮失效约占60%以上，主要体现为：弯曲力矩造成的轮齿折断，接触应力产生的齿面疲劳点烛和磨损，因此说，齿轮失效与齿轮啮合过程的受力以及应力分布有关。齿轮在实际的啮合过程中，由于接触状态的不断改变、接触刚度的变化以及齿轮加工误差以及轮齿受载变形等使得齿轮的实际啮合状况较为复杂，在理论啮合线外发生啮合、产生啮入啮出冲击等等。传统的设计往往根据以往经验，进行静强度设计计算，通过降低许用应力和加大许用安全系数提高设计可靠性。随着计算机技术和有限元分析技术的发展，适用于机械传动有限元分析软件越来越成熟，该文应用ANSYS软件对渐开线斜齿轮副进行动力接触有限元分析，研究轮齿齿面的接触状态、啮合特性以及应力变化规律，基于ANSYS中的疲劳寿命预测软件FE-SAFE对齿轮进行疲劳寿命预测。

力学性能及疲劳寿命预测设计流程如图1所示。首先根据设计参数建立实体模型，进行静强度分析计算；利用ANSYS软件建立齿轮副有限元模型并加载求解，获得齿轮应力分布规律、确定危险位置；将有限元模型导入ADAMS中进行动力学仿真分析，获得载荷谱；采用疲劳强度分析理论，结合材料疲劳S-N曲线、载荷谱，依据Miner 疲劳累积损伤法则，对齿轮副危险位置进行疲劳强度分析，预测疲劳寿命，验证设计要求 [2] 。

1 斜齿轮三维实体建模

1.1 三维实体建模过程

该文利用UG的关系表达式法进行渐开线齿轮参数化三维建模，建模过程：（1）根据设计条件，分析基本参数和齿轮结构；（2）建立齿轮几何结构关系表达式、渐开线等关键曲线数学模型；（3）将关系表达式导入UG中；（4）在UG环境下绘制齿轮基本圆（基圆、齿顶圆、齿根圆），绘制渐开线、过渡曲线、螺旋线等，修剪获得单齿轮廓线；阵列轮齿，将齿廓曲线沿导引线进行拉伸；绘制轴孔、键槽、倒圆角等。

1.2 渐开线斜齿轮齿廓方程和几何结构关系表达式

1.2.1 斜齿轮齿廓方程

（1）渐开线方程。根据渐开线形成原理[3]，推导得渐开线齿廓直角坐标方程：

（1）

（2）过渡曲线方程

当采用齿条型刀具加工齿轮时，过渡曲线方程：

（2）

式中，各参数含义见参考文献[4] 。

1.2.2 齿轮几何结构关系表达式

斜齿轮基本参数包括：齿数z、法面模数mn，法面压力角α、齿宽b等。在UG中建模前，需对所有基本参数赋初始值。

分度圆直径d=mn*z/cos（β）；基圆直径db=d*cos（α）；

齿顶圆直径da=d+2*ha；齿根圆直径df=d-2*hf 。

打开UG，将表达式输入到“表达式”对话框中，进行UG建模。

2 斜齿轮传动过程中的载荷变化及应力变化规律

2.1 齿轮传动载荷分析

2.1.1 齿轮传动啮合状态分析

为确保斜齿轮传动平稳可靠，斜齿轮传动重合度通常大于1。所以，齿轮传动过程中存在着单齿与双齿交替啮合现象[5]，齿轮啮合状态及载荷分布如图2所示。图中M点为啮合点，ABCD为实际啮合线（一个啮合周期），AB、CD段为双齿啮合区域，BC段为单齿啮合区域。轮齿刚进入啮合A点时，承担全部载荷的40%，从双齿啮合区域过渡到单齿啮合区域过渡点B时，承担全部载荷的60%，迅速转入单齿啮合区域，当到达B点时轮齿承担全部载荷的100%，D点承担载荷又恢复到40%。一个啮合周期内，在A、B、C、D处经受四次冲击作用，其中，B点载荷最大。

2.1.2 齿轮传动力学模型

齿轮啮合过程中，单齿啮合时只有一对轮齿啮合，齿轮只受一个啮合力F作用，F =T/r，r为小齿轮分度圆半径。

双齿啮合时有两对轮齿啮合，受到F1和F2作用。在F1和F2作用下主动轮和从动轮上的轮齿将发生较大的弹性变形，包括绕曲变形和接触弹性变形。为简化计算在啮合力计算时忽略了轮齿弹性变形，且设F1与F2相同，F1=F2=T/2r。

2.1.3 齿面接触应力及齿根弯曲应力计算

外啮合传动斜齿轮齿面接触应力[6]：

（3）

斜齒轮齿根弯曲应力：

（4）

式中，Ft为齿轮分度圆切向力，d—小齿轮分度圆直径，b—工作齿宽，i—传动比，mn—法向模数，其它参数见参考文献[6] 。

2.2 齿轮应力计算实例

已知斜齿轮副传递功率为7500 kW，转速为1500 r/min，材料为20CrMnMo，渗碳淬火处理，齿轮几何参数及材料性能参数如表1所示。

2.2.1 接触应力分布规律

利用MATLAB编程进行齿轮接触应力分布以及齿轮弯曲应力分布计算。

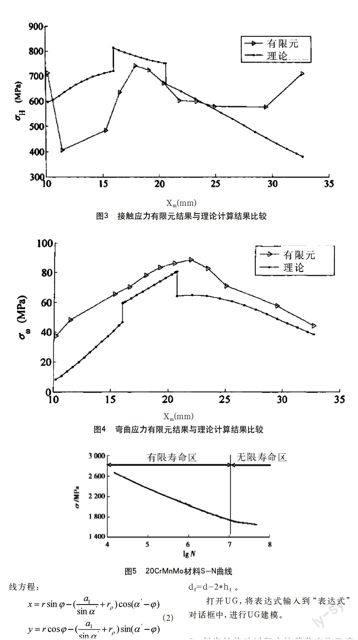
研究表明，齿轮啮合过程中，不同的啮合位置齿轮接触应力不同，选取齿轮啮合过程中多个啮合点进行轮齿应力计算，接触应力分布曲线如图3所示。图形显示，齿面接触应力的变化规律与载荷变化规律具有一致性，齿轮齿面接触应力在单、双齿啮合状态交替时齿轮的载荷及应力发生突变，双齿啮合区域的齿轮接触应力较小，单齿啮合区域接触应力较大，齿面接触应力最大值约为815 MPa，此处为接触疲劳危险位置（B点）。

2.2.2 弯曲应力分布规律

与分析接触应力一样，选取齿轮啮合过程中多个啮合点进行应力计算。齿轮在啮合力Ft和径向力Fr作用下，齿根处产生的弯曲应力如图4所示。图形显示，齿根弯曲应力分布与齿轮接触应力分布区别很大，齿根弯曲应力分布的最大值出现在单齿啮合状态再次进入双齿啮合状态的位置，弯曲应力最大值约为80MPa，对应的截面即为危险截面（C点）。

3 斜齿轮副有限元分析

3.1 有限元分析软件

（1）ANSYS软件。ANSYS软件是美国 ANSYS公司研制的有限元分析软件，通过异构的CAD软件接口，实现数据的共享和交换。软件包括三大模块：①前处理模块，其中的实体建模及网格划分工具，用于构造有限元模型；②分析计算模块，进行结构分析、动力学分析、灵敏度分析和优化分析；③后处理模块，将计算结果以彩色等值线、图形和图表等形式显示或输出。

（2）LS-DYNA动力分析软件。LS-DYNA 是非线性显式分析程序包，具有功能强大的单元库，二维、三維实体单元以及Lagrangian 单元等，特别适合于分析各种非线性结构冲击动力学问题。由于斜齿轮啮合过程中两齿面接触位置不断变化、接触应力和弯曲应力大小也在变化，属于非线性行为，本章应用ANSYS/LS-DYNA软件，对渐开线齿轮副进行动力仿真分析。

（3）ANSYS/FE-SAFE。ANSYS/FE-SAFE是进行结构疲劳寿命分析的专用软件，由用户界面、材料数据库管理系统、疲劳分析程序等组成。FE-SAFE 软件综合多种影响因素（如应力集中、平均应力、表面光洁度等），按照累积损伤理论，根据应力或应变进行疲劳寿命分析设计，也可以根据疲劳材料以及载荷的概率统计规律进行疲劳可靠性设计。

3.2 斜齿轮副有限元分析过程

3.2.1 接触算法

对斜齿轮进行有限元分析时，必须进行无穿透约束，防止有限元分析中相互穿过，施加无穿透约束方法有三种：罚函数法、拉格朗日乘子法和增广拉格朗日乘子法。本文选用增广拉格朗日乘子法进行分析，此方法是罚函数法和拉格朗日乘子法的结合，其中，罚函数法是通过将力和位移的关系转化成接触力和接触面的穿透来实现的，用罚因子来调节；拉格朗日乘子法是通过拉格朗日乘子增加一个附加自由度来施加接触体必须满足无穿透约束。在接触初始状态，接触条件由罚因子决定，当接触达到平衡时，由拉格朗日乘子检查两接触表面的穿透值，此方法能精确控制接触条件，获得满足精度的接触力。

3.2.2 接触方式

ANSYS支持三种接触单元：点-点接触单元，点-面接触单元和面-面接触单元。点-点接触适用于知道确切的接触位置，且相对滑动较小的情况，单元类型一般选择CONTA178；点-面接触适用于接触面未知而且允许接触面之间有较大滑动，单元类型有CONTAC48和CONTAC49；面-面接触适用于大滑动和摩擦大变形的接触情况，主要单元类型有TARGE169-TARGE170及CONTA171-CONTA174。

3.2.3 有限元分析过程

建立接触模型及网格划分：本文利用 Hypermesh对齿轮进行六面体网格划分，然后将有限元网格模型导入到ansys进行有限元分析。为保证分析精度和效率，对接触区域和齿根部进行局部网格细化，其它区域网格相对粗糙[7]；定义单元类型及材料属性：选用solid45单元对斜齿轮副进行有限元网格划分，齿轮材料选为20CrMnMo，材料性能参数见表1；创建齿轮模型接触对：由于斜齿轮副轮齿接触面有较大的滑动和摩擦变形，接触单元类型选择TARGE170和CONTA174，分别将主动轮和从动轮上可能发生接触的表面定义为接触面和目标面。将接触刚度因子FKN设置为1，拉格朗日算子允许的最大渗透量FTOLN设置为0.1；施加边界条件和载荷：由于Solid45单元只有三个位移自由度，因此扭矩不能直接施加在模型上，根据等效平衡原理将施加在齿轮上的扭矩转化为作用在主动轮齿轮轴孔圆周上的切向力，切向力的合成结果与扭矩等效；求解与后处理：选取啮合周期内多个啮合点，通过MATLAB编程计算不同啮合点的应力，采用插值法拟合出不同啮合位置的最大等效接触应力和等效弯曲应力分布规律（图3、图4）。

3.3 有限元分析与理论计算结果比较

（1）齿面接触应力分析结果与理论计算结果比较。为比较有限元分析结果与理论计算结果，将两者绘制在一张图中，如图3所示。图形显示，在一个啮合周期内齿轮最大齿面接触应力和最大等效接触应力变化规律相似，有限元分析结果小于理论计算结果，两者在单双齿啮合状态变化趋势基本一致。在啮入和啮出时ANSYS计算结果比相应的理论计算结果大，说明齿轮啮入和啮出时齿顶会产生应力集中。

（2）齿根弯曲应力分析结果与理论计算结果比较。ANSYS分析计算结果与理论计算结果比较如图4所示，ANSYS分析结果稍大于理论计算结果，但两者整体趋势一致。

3.4 齿廓修形

该文只研究了齿顶修缘对齿轮寿命的影响，修形后的齿轮最大接触应力值由815MPa降低到284MPa，应力改善约为65%，降低应力集中、减少啮合冲击，延长齿轮使用寿命。

4 齿轮疲劳寿命预测

4.1 齿轮疲劳寿命计算方法

齿轮传动失效是由一系列的循环载荷所产生的疲劳损伤累积造成的，当损伤累积达到临界状态时，零件将发生断裂，导致疲劳失效。本文采用线性疲劳累积损伤法则Miner进行疲劳寿命预测，该理论认为试件在给定的应力或应变循环下，损伤与应力循环次数成线性累积关系，当累积值达到1时，齿轮发生疲劳破坏，表达式：[8]。

4.2 齿轮疲劳寿命计算

（1）确定齿轮疲劳危险位置。ANSYS有限元分析结果中的最大等效接触应力和最大等效弯曲应力位置最易出现疲劳裂纹，导致疲劳失效，将此位置定义为疲劳危险位置。

（2）确定齿轮载荷谱和疲劳危险位置应力谱

载荷谱：齿轮啮合周期与轮齿啮合点位置和齿轮转速有关，T啮合=60θ/2πn。通过MATLAB编程计算，并绘制齿轮啮合受力与时间关系，得到载荷谱。

疲劳危险位置应力谱：啮合周期内齿轮受载呈周期性变化，齿轮接触疲劳危险位置的接触应力分布规律也呈周期性变化，接触疲劳危险位置的应力分布规律与啮合时间的相互关系就是疲劳危险位置应力谱。

（3）建立齿轮材料S-N曲线。S-N曲线反映材料的抗疲劳性能，通过材料的疲劳强度实验数据绘制，其表达式为mlgσ+lgN=lgC，将20CrMnMo材料的m、c及其它参数值代入公式，绘制的S-N曲线如图5所示。

（4）接触疲劳寿命分析。表1数据显示，当可靠度为99%时，齿轮的持久寿命循环次数为5*l07次，齿轮的接触疲劳极限为1572 MPa，该文接触疲劳危险位置处的最大等效应力为815 MPa，远小于材料的接触疲劳极限，说明齿轮接触疲劳寿命位于无限寿命区域。

4.3 影响齿轮寿命参数

齿轮疲劳寿命预测中，许多因素只在理想状态下进行分析，忽略了齿轮制造误差、齿轮受载变形、啮合冲击等因素。研究表明，齿轮啮合过程中，影响疲劳寿命的主要因素包括载荷、模数、压力角、粗糙度等[8]。

（1）载荷对接触疲劳寿命的影响。通过将齿轮载荷放大或减小来观察载荷对齿轮副疲劳寿命的影响。0.75倍额定载荷时，斜齿轮副均为无限寿命；1.5倍额定载荷时，主、从动轮疲劳寿命分别降低42%和38%。数据表明，随着载荷的增加，齿轮的疲劳寿命逐渐降低，因而在齿轮传动中应该适当控制载荷的大小，保证齿轮疲劳寿命。

（2）模数对齿轮寿命影响。当齿轮传递的功率和转速以及其他参数保持不变时，齿轮分度圆直径会随着模数增大而增大，齿轮传递的载荷随之减小，齿轮疲劳寿命也将随之提高。而且齿轮由双齿啮合状态进入单齿啮合、再重新进入双齿啮合的过程将放缓。

（3）压力角对齿轮寿命影响。齿轮啮合过程中所受载荷随着压力角的增大而增大，但是影响并不明显，但对齿轮双齿啮合与单齿啮合状态的分配影响很大，压力角越大，齿轮处于单齿啮合状态的区域越大，齿轮疲劳寿命会降低。

（4）齿面粗糙度影响。齿轮表面缺陷在承受交变应力时易出现应力集中，加速疲劳破坏。为研究表面粗糙度对齿轮副寿命的影响，通过使用不同等級粗糙度进行疲劳寿命计算，数据表明，齿轮副的疲劳寿命随着齿面粗糙度的增加而减小。

5 结语

研究表明，在使用有限元方法进行齿轮应力分析的基础上，拟合出齿轮接触应力分布和齿根弯曲应力分布曲线，通过将理论计算结果与有限元分析结果相比较，验证了利用有限元分析方法进行齿轮疲劳寿命预测是可行和正确的。结合材料S-N曲线，基于疲劳损伤理论对斜齿轮副进行疲劳寿命预测，符合齿轮传动机构设计和运行的实际情况。

参考文献

[1]陈辰嘉.小倾角齿轮箱变厚斜齿轮副啮合性能仿真及疲劳寿命分析[D].重庆：重庆大学，2013.

[2] 时慧焯，孙金辉.基于有限元法的电机车驱动轴疲劳寿命预测[J].大连交通大学学报，2014（A01）：51-54.

[3] 张策.机械原理与机械设计[M].北京：机械工业出版社，2011：202-508.

[4] 李科.基于UG人字形齿轮参数化设计及动力学仿真[D].河北：河北科技大学，2013.

[5] 鲍洪.直齿渐开线圆柱齿轮力学性能及疲劳寿命计算方法研究[D].上海：华东理工大学，2011.

[6] 全国齿轮标准化委员会.GB/T 3480-1997渐开线圆柱齿轮承载能力计算方法[S].北京：中国标准出版社，1997：7-11.

[7] 孙胜苗，龚宪.空气压缩机用高重合度斜齿轮副的疲劳寿命分析[J].机械科学与技术，2014（8）：1136-1140.

[8] 林腾蛟，沈亮等.风电增速箱输出级齿轮副疲劳寿命有限元分析[J].重庆大学学报，2012（1）：1-6.