继电器的可靠性(寿命)表征及求解简介
郑天丕,梁坚平,王水君,赵玲玲
(宁波福特继电器有限公司,浙江宁波,315012)
综述与简介
继电器的可靠性(寿命)表征及求解简介
郑天丕,梁坚平,王水君,赵玲玲
(宁波福特继电器有限公司,浙江宁波,315012)
本文介绍两种可靠性表征及求解法。其中详细介绍Weibull函数的图解法及最大似然估计法,并列举三个典型的折线Weibull的图解法,着重介绍Weibull分布的两个参数、形状参数(m)、和征寿命(η)及使用寿命B10的置信度区间的求解办法,并指出累计危险方格绘图纸图解及最大似然估计法的缺陷。
使用寿命;失效率;折线Weibull;最大似然估计法;置信度
1 引言
用户常问:“既然厂家给了使用寿命(额定寿命),为什么在使用寿命次数内还会有产品失效?使用寿命期间,每动作一次的失效几率有多少?”“厂家是如何确定产品的使用寿命?靠得住吗?有多少可信度?”为此,我们在这里介绍产品寿命的可靠性表征及其解(包括置信度),起着抛砖引玉作用。
2 可靠性的表征
早期寿命的可靠性被定为额定寿命区间的最大失效率。以MIL 为例,其出发点是假设寿命区间的失效率是恒定的,与动作次数无关。军方也承认恒定失效率的假设有时是不对的,但它提供一个合适的比较数据。其代表M6106 、M39016、M83536等。而IEC则是瞬间时失效率来表示,失效率与动作次数(时间)有关。其代表为IEC255-0-20、IEC60255-23。 MIL规定:鉴定时置信度取90%,维持鉴定取60%。置信度:“估计是正确的概率”(即可信度)。IEC没明确规定是置信度,一般为60% 左右。
本世纪初出现用使用寿命来表示可靠性。使用寿命(useful Life):“连续循环次数或时间,直到确定的失效百分数为止。”IEC61810-2:2005、2015规定:“这个百分数本标准定为10%。”MIL-PRF-32140:2004规定:“这个百分数最大为1%”。换句话说,在使用寿命期间(额定寿命)会有10%或1%的产品失效。或且说IEC规定寿命的可靠性为90%,MIL规定寿命的可靠性至少为99%。若是有可靠性指标的产品,还要加上置信度进行修改。IEC为90%,MIL为95%。可靠性的两个典型表征如表1所示。
是否提供有可靠性指标的产品,MIL 与IEC截然不同。MIL 规定是强制性的,厂家必须满足军方提出的各项指标,包括寿命次数、失效率及置信度。IEC却规定可靠性指标是非强制性的,由厂家自己决定,提出来供用户使用。但一旦提出,其置信度必须是90%。

表1 寿命可靠性的两种表征
3 求解
3.1 Weibull分布的有关符合号及表达式
f(t ) 概率密度函数
(1)
F(t) 累计分布函数(失效的概率)
(2)
R(t ) 可靠性函数(存在的概率)
(3)
h(t) 危险函数(瞬时失效率)
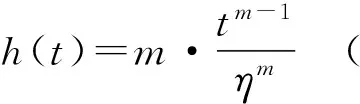
(4)
H(t) 累计危险函数
(5)
t次数或时间
mWeibull函数的形状参数
ηWeibull函数的尺度参数(又称特征寿命)
3.2 weilbull函数的求解
IEC和MIL都是用Weibull函数来求得使用寿命。
3.2.1 图解法
3.2.1.1Weibull概率纸
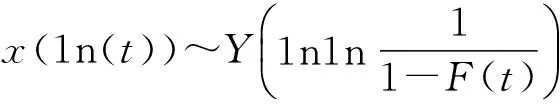
3.2.1.2Weibull图解原理
图解的关键是求F(ti),即中位秩的求法,有:
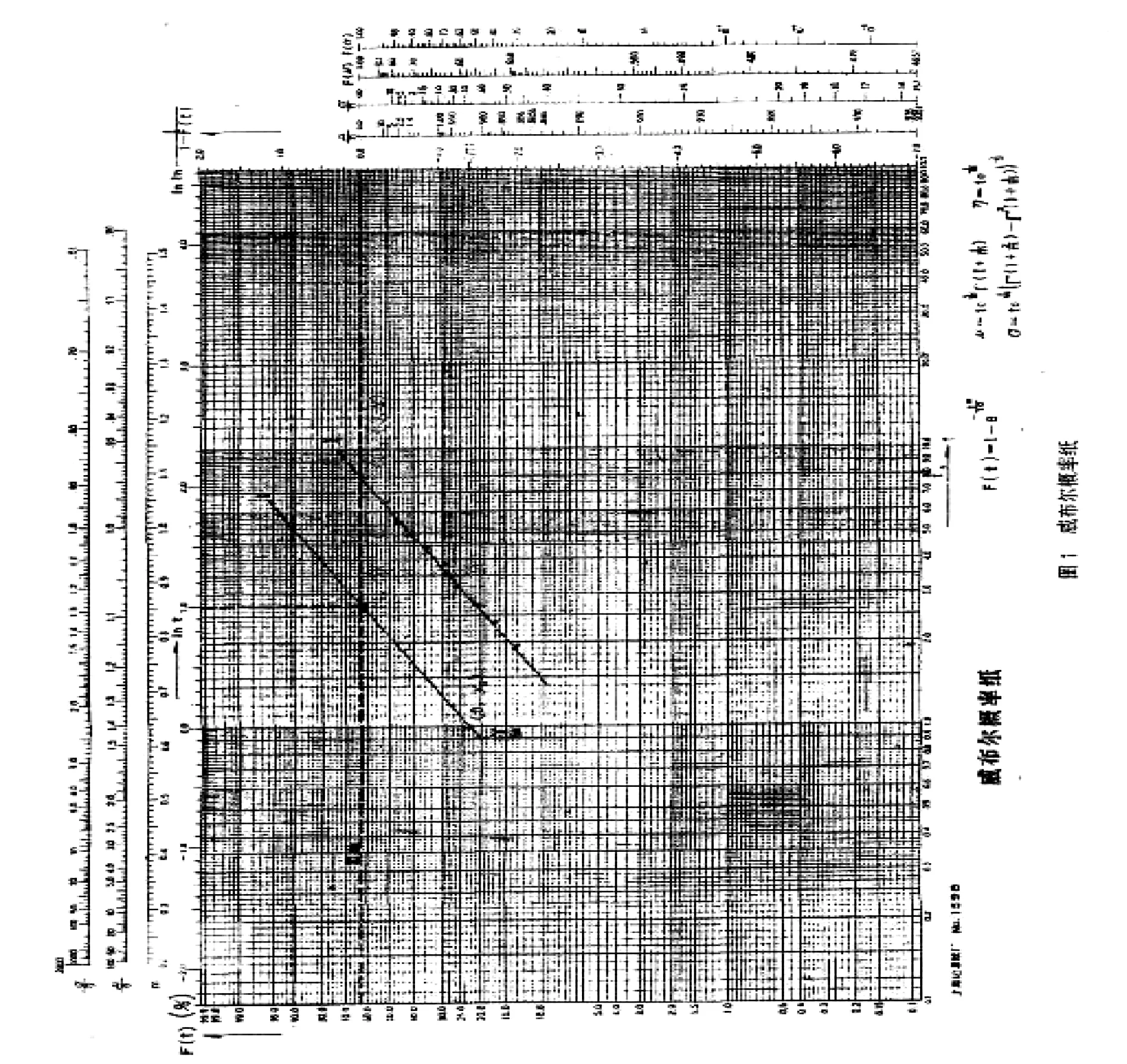
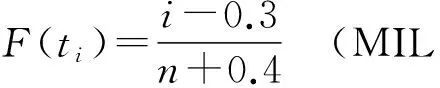
(6)
这里n为试验样品数,i为失效序数。因为F(ti )是服从自由度为(n +1-i)的β分布,中位秩实际是置信度为50%的β0.5(n+1-i)的分位点的值,(6)式是它的高度近似值。
有了F(ti)就可以列出(ti-F(ti)的对照表,同时应填上失效模式,然后在Weibull概率纸上描点(ti-F(ti)的点,最后回归成一直线。
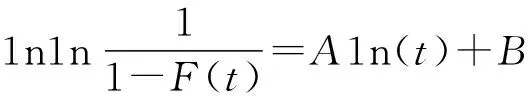
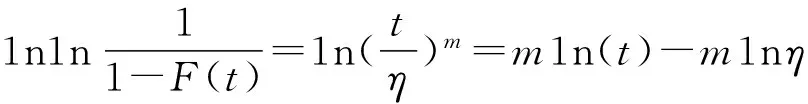
∴A1n(t)+B=m1n(t)-m1n(η)=Y
当y=0(F(to)=0.32)时,x轴与回归线的交点为(tη0),则有:
Y=m1n(tη)-m1n(η)=0
∴1n(tη)=1n(η)η=tη
回归线与x轴的交点所对应的tη即为η值。
平移回归线过(1,0)点,其斜率不变,则其与y轴的交点所对应的y值即为(-m)。
找出F(t10)=10%的横线,它与回归线的交点,所对应的t10值即为B10。
3.2.2 累计危险方格绘图纸图解
累计危险方格绘图纸如图2所示。正常坐标:(t-H(t))为对数划分,无(0 0)点。中间坐标x[ln(t)]-y[ln(H(t))]等分,无划分线,仅在上方及右侧刻上等分标尺,表示(xy)值。

结果是累计危险方格绘图纸的x-y坐标与Weibull概率纸的x-y坐标完全一样,故m,η的求解也与Weibull概率纸的求解一样。

图2 累计危险方格绘图纸
B10的求解,按定义B10所对应的t10有F(t10)=10%

所以,累计危险方格绘图纸图解中,H(t10)=10.54%的横线与回归线交点所对应的t10便是B10的值。
3.2.3 折线Weibull(DoglegWeibull)
当试验所得的数据在Weibull概率纸上(或在累计危险方格绘图纸上)不能回归成一直线时,即是折线Weibull。其原因是有多个失效模式或失效因素引起的。所以在列出ti-F(ti)或ti-H(ti)时,在其表格中应填上对应的失效模式。出现折线Weibull时,可按不同的失效模式各自回归成直线。也可以重新调整失效细节,失效原因加以分析,改进后重新进行试验。
3.2.4 例举
我们在这里列举三个典型折线Weibull图解的例子,供参考。
例1 某产品阻性负载:16A/120VAC,循环率速1800次/h,负载比:1:1。n=13c=9。具体数据列入表2。按表2的数据,在Weibull概率纸上不能回归成一直线(见图3中的“x”点)。去掉“架化”的产品,重新列表,如表3所列。再在Weibull概率纸上描点(图3中的“·”),回归成一直线。求得m=2.3 、η=14.0×104、B10=4.9×104次。

表2 例1 某产品的试验表格

表3 例1中触点失效的数据
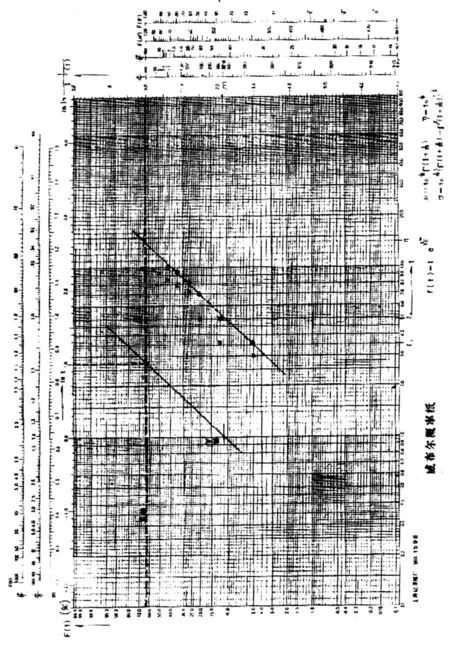
图3 阻性,16A×120VAX试验的成布尔图
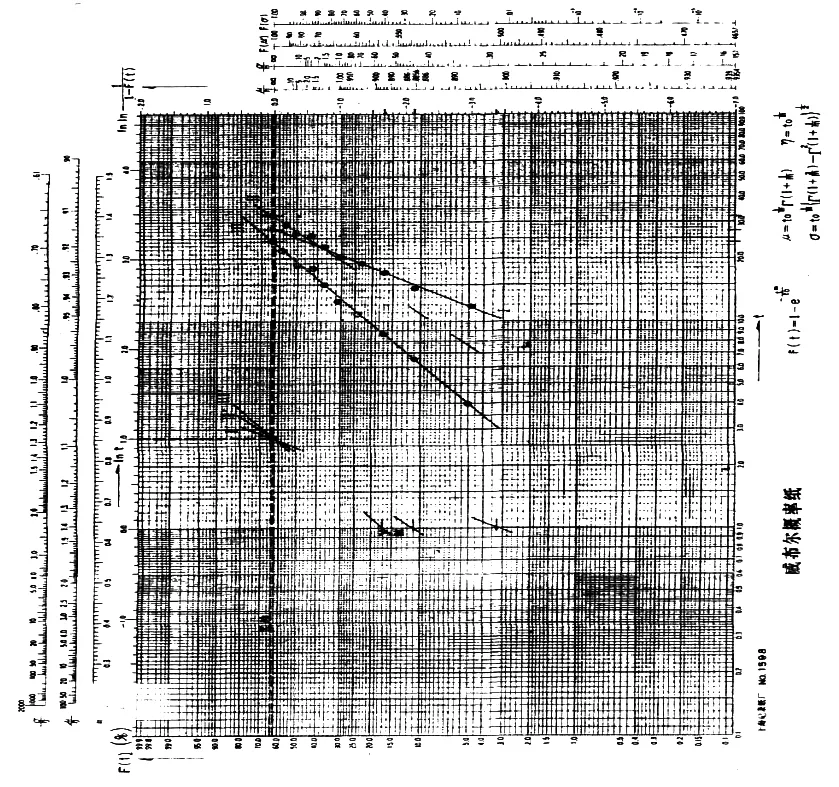
图4 阻性负载试验的成布尔图
例2 某产品的试验,n=15c=10。具体数据如表4所列,在Weibull概率纸上描点,回归成两条直线,直线Ⅰ和直线Ⅱ,如图4所示。
对直线Ⅰ有:m1=3.4η1=27.2×105B10=14.5×105
对直线Ⅱ有:m2=2.1η2=32.4×105
此例在经典教科书中取Weibull位置参数γ=8.0×105次。取Ti=ti-8×105,结果也把Ti填入表4,并在Weibull概率纸上描点,回归成直线Ⅲ(如图4所示)。结果有m3=1.6,η3=24.5×105。这是值得讨论的。
这里必须指出,按经典的Weibull理论,当t0≤γ时,有F(t0)=0,λ(t0)=0!对此例来讲,t0取8×105时,有F(8×105)=0,λ(8×105)=0。这个结果是值得讨论的。任何一个负责的厂家都不会说自己的产品在使用寿命的某一区段,其失效率为零。没有产品会失效。其实,从概率统计理论的观点来看,任何产品在其使用期内的任何一个区段都有可能发生失效,只是概率多少不同而已。同时就本例来讲,当t0=8×105时,对直线Ⅰ有Fi(8×105)=1.2%;直线Ⅱ有F2(8×105)=5.5%;直线Ⅲ有:F3(8×105)=15.0%。显然与F(8×105)=0自相矛盾,故位置参数不可取。
就本例来讲,我们认为应取直线Ⅰ的数据为该产品的可靠性参数,即m=3.2、η=27.2×105次、B10=14.5×105次。因为直线Ⅱ的因素要等到工作22×105次之后才起作用,大大超过使用寿命期。换句话说因素Ⅱ要到产品寿终正寝之后才起作用,才影响产品,所以不予考虑。

表4 例2 产品的试验数据
例3 累计危险方格绘图纸图解
本例摘自IEC61810-2:2015(3)征求意见第二稿(符号有所更改)。图解步骤如下:
1)秩的评定估计 Ki=n+1-i
2) 危险值h(ti) h(ti)=1/Ki=1/(n+1-i)
(7)
(8)
4) 在累计危险方格绘图纸上描上[ti(H(ti)]的点。
5)按不同的失效模式各自回归成一直线。本例有两个失效模式,回归线成两条直线,如图5所示。
本例具有试验数据为:n=30,c=27 ,失效模有两个,具体数据见表5。结果有:m1=3.55η1=10.66×105,B101=5.60×105次;m2=7.46η2=2.25×105B102=6.10×105次。

表5 数据及处理结果

图5 累计危险图
以下几点值得商榷:

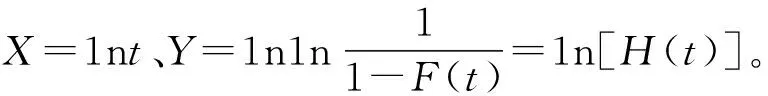
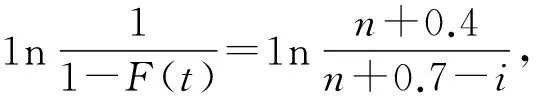
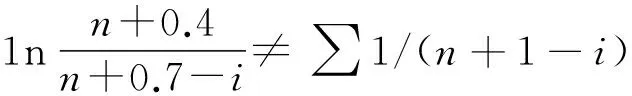
c)IEC61810-2:2015的一项主要任务是求产品的使用寿命,即B10。尽管本例中求得两个B10,但它们都不是该产品的B10。因为取其中的任何一个B10,另一个因素也在起作用,综合起来的累计失效百分数自然大于10%。对于两个及以上影响因素的产品的可靠度,按概率统计理论,产品的可靠度R=R1·R2…RN。即串联因素的可靠度,R=∏NRi。就本例来讲,有R=R1·R2。故取B10=5.2×105次。则有:R=R1·R2=92%×97%=89.3%。产品的累计失效百分数F(5.2×105)=1-R(5.2×105)=1-0.893=10.7%。所以,本例产品的B10应为5.2×105次。
d)在累计危险方格绘图图解中,B10是H(t10)=10.54%的横线与回归线相交的点所对应的t10值。具体操作时,H(t10)=10.54%的确定比较难,且误差较大。
3.3 最大似然估计法
用最大似然估计法求解Weibull函数有两个公式,下列第一个式子(9)式是用来求m的,然后用m及第二个式子(10)式来求η。
(9)
这里,n为样品数,c为失效数,T为试验终止时的循环次数。
(10)
(11)
(12)
IEC61810-2:2005、IEC61810-2:2015注明:任何一台能解方程的计算机都可用来求解(9)式的m,并能很快地收敛到一个简单的值(asinglevalue)。可见最大似然估计法(MIL)的解只有一个m。这意味着是直线Weibull。但实际上许多场合是折线Weibull。要判定一组试验数据是否是直线Weibull,按M32140:2004的规定,其线性系数γ应≥0.8。即
就是等于首先要用Weibull概率纸图解法求得Xi,Yi,方能判断一组数能否满足(13)式要求。既然如此,用Weibull概率纸图解也已完成大半,何必终止。其实只要做过几次图解法之后,自然不必去求线性系数,凭经验就可判明所描出的(Xi,Yi)的点能否回归成一直线。
4 置信度区间
4.1 m的置信度区间
q=c/n,k=2.14628-1.361119q
β1=Χ2[(c-1)kα]
β2=Χ2[(c-1)k(1-α)
]这里,Χ2[(c-1)kα]是自由度为(c-1)k的Χ2分布的α分位点。
修正系数:
那么,m的置信度区间:[w1mw2m]
这里,m用(9)式求得。笔者认为也可用图解法求的。
4.2 η的置信度区间
a)c A5=0.2445(1.78-q)(2.25+q) A6=0.029-1.083ln(1.325q) A3=-A6Χ2 x=μ(1-α)是正态分布的(1-α)分位点。μ(1-α)=-μa. 表6 正态分布的分位点 b)c=nd3=t(1-α)(n-1) 这里,t(1-α)(n-1)是自由度为(n-1)的t分布的(1-α)分位点的值。 η的置信度区间为:(A1ηA2η) 这里的m用(9)式求之,η用(10)式求得。笔者以为也可用图解法求之。 4.3 B10的下限 B10L=QB10 B10用(9)计算。笔者以为也可以用作图法求得。按IEC61810-2:2005的规定,置信度(1-α)取90%。 5.1 用Weibull 分布求解 由于军方已规定使用寿命次数(ti)及置信度为95%。所以,置信度是用修正F(t)的办法来求解。要求厂家满足(14)式要求。即: (14) 这里,3.0是置信度为95%的修正系数。试验数据是用Weibull概率纸图解,找出ti的纵线与回归线相交点所对应的F(ti),要求F(ti)满足(14)式规定。注意,M32140:2004规定做图时线性系数γ≥0.8。 5.2 按指数分布求解 指数分布是Weibull分布中m =1的特例。它是假设寿命期间失效率(λ)与时间或动作次数无关。其失效率λ有: i=1.2…n (15) (1-α)为置信度,c为失效数,n 为试验样品数,T0为试验总次数。试验是按额定寿命次数定时截尾进行,无替换。 为了便于试验人员操作,GJB65B(idtM39016E)特地列出置信度为90%和60%两个C与T0的对照表。这样就可以不必去查Χ2表进行计算就可以判定产品合格与否。 以上的介绍可知继电器的寿命是用Weibull函数来求解。Weibull分布有两种情况:直线Weibull和折线Weibull。以前一般用直线Weibull来求解,但大多数场合是折线Weibull。 1)直线Weibull的求解 a)用Weibull概率纸和累计危险方格绘图图解,求得m η和B10。对于可靠性指标的产品应按置信度大小加以修正。来求得m η的置信度区间及B10的下限B10L。IEC为90%的置信度。 b)最大似然估计法,因为最大似然估计法只求得一个m值,即直线Weibull。这就要求在一组试验数据的求解之前要判定它是否是直线Weibull ,即它的线性系数γ≥0.8。这就得借助图解法方可求得。这是最大似然估计法的缺点之一。 2)折线Weibull的求解 求解的第一步,在列出ti-F(ti)表格时,务必填上相应的失效模式,以便回归。 a)多个零部件失效:可按各自的ti-F(ti)进行回归,求解。然后,对相应的零部件进行分析。改进之后再进行试验。 b)不同时期起作用的因素:在图解时按不同因素回归,只对含使用寿命(额定寿命)期限内的点进行回归,求得m、η、B10和B10L。 c)同时起作用的因素分别求得各因素的mη。但其使用寿命B10,则要用串联可靠度的方法求产品的R。 ,此时t10即是B10。 3)MIL的求解 由于军方已定好使用寿命t1及置信度,故按M32140的做法,只用Weibull概率纸图解。求得m、η后应满足3.0F(t1)≤1%。3.0为95%置信度的修正系数。 4)笔者认为,在求解时最好用Weibull概率纸图解,在列ti-F(ti)表格时应加上对应的失效模式以便回归分析。 参考资料: [1] IEC61810-2:2005;IEC61810-2:2015[S]. [2] MIL-PRF-39016F:2005;MIL-PRF32140:2004[S]. [3] 陆俭国. 电工产品可靠性 [M],北京:机械工业出版社,1991. [4] 郑天丕,方珍. "使用Weibull函数的一点体会"[J] 机电元体, 2001(2). 2015-09-21 10.3969/j.issn.1000-6133.2015.05.011 TN784 A 1000-6133(2015)05-0039-08
5 MIL的求解
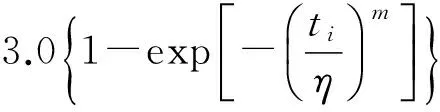
6 总结

