交替方向Galerkin方法在偏积分微分方程中的应用

王 佳, 黎丽梅, 王 易, 王怡芬, 欧阳欣

(湖南理工学院 数学学院, 湖南 岳阳 414006)

交替方向Galerkin方法在偏积分微分方程中的应用

王 佳, 黎丽梅, 王 易, 王怡芬, 欧阳欣

(湖南理工学院 数学学院, 湖南 岳阳 414006)

用交替方向Galerkin方法研究二维带有弱奇异核的偏积分微分方程的数值解, 在空间方向上, 采用线性有限元, 时间方向上采用向后欧拉方法, 积分项用一阶卷积求积逼近, 该方法既具有交替方向存储量少, 计算量低, 又具有有限元高精度的特点.

偏积分微分方程; 交替方向隐式方法; 向后欧拉方法; 有限元方法

引言

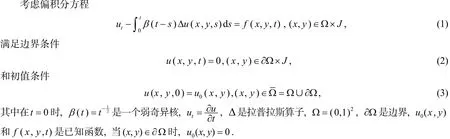
此问题常出现在带有粘弹性流体模型及带有记忆功能的热传导方程中, 因此讨论这类偏积分微分方程的数值求解具有非常重要的意义. 近年来有许多文献研究它们的数值解(例如Sanz-senrna[1], Lòpez-Marcos[2], Chen et al[3], Tang[4], Sun[5], Xu[6,7], G. Fairweather[8],W. Mclean, V. Thomée[9,10]). 他们有的用有限元法[3,6,7,11], 有的用差分法[1,4,5], 有的用样条配置法[8], 但很少用交替方向有限元方法. 交替方向有限元法最大的优点是能把多维问题转化为一维问题来计算, 大大地减少了计算量. 本文主要是利用交替方向有限元法研究二维偏积分微分方程的数值解, 在空间方向上采用有限元, 时间方向上使用后欧拉方法, 积分项采用一阶卷积求积逼近.

1 预备知识

2 Galerkin交替方向的格式

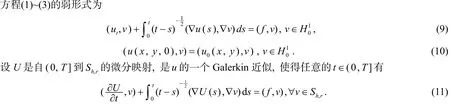
3 数值例子

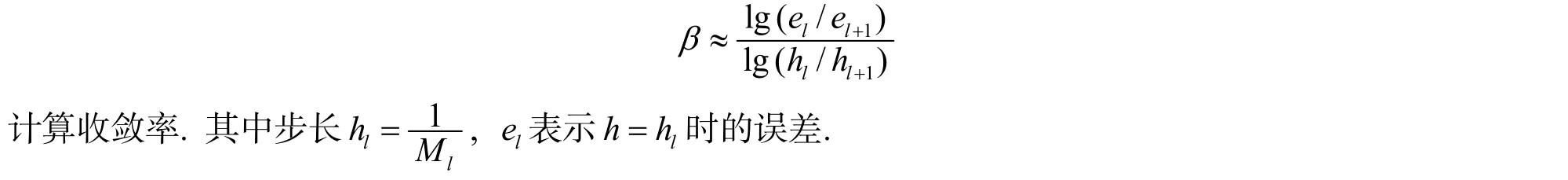
初值用U0=W0来逼近, 在T=1时, 用交替方向有限元方法计算出的结果列于表1和表2中. 在表1和表2中, 我们分别选时间步长k=h和k=h2, 来得到相应的误差和收敛率.

表1 在k=h时的误差和收敛率

表2 在k=h2时的误差和收敛率

4 结论

本文用交替方向有限元方法对形如式(1)的偏积分微分方程进行了数值求解. 在求解过程中, 空间方向上采用有限元, 时间上采用向后欧拉方法, 积分项用一阶卷积求积逼近. 用这种离散格式对偏积分微分方程进行数值求解, 在误差和精度方面都达到了令人满意的结果, 并且计算也非常简便. 这说明用交替方向有限元方法求偏积分微分方程的数值解是切实可行的.

[1] J. M. Sanz-sern.A numerical method for a partial integro-differential equation[J]. SLAM J. Numer. Anal, 1988(25): 319～327

[2] J. C. Lòpez-marcos.A difference scheme for a nonlinear partial integro-differential equation[J]. SIAM J.Numer.Anal, 1990(27): 20～31

[3] C. Chen, V. Thomée, L. B. Wahlbin.Finite element approximation of a parabolic integro-differential equation with a weakly singular kernel[J]. Math. Comput, 1992(58): 587～602

[4] T. Tang.A finite difference scheme for a partial integro-differential equation with a weakly singular kemel[J]. Appl. Numer. Math, 1993(2): 309～319

[5] Z. Sun, X. Wu.A fu1lly discrete difference scheme for a diffusion-wave systym[J]. Appl. Numer. Math, 2006(109): 193～209

[6] D. Xu.Uniform L behavior for time discretization of a Volterra equation with completely monotonic kernel II:convergence[J]. SIAM J. Nnmer. Anal, 2006 (46): 231～259

[7] D. Xu.Stability of the difference type methods for linear Volterra equation in Hilbert spaces[J]. Numer. Math, 2008(109): 571～595

[8] A. K. Pani, G. Fairweather, R.I.Fernandes.ADI orthogonal spline collocation methods for parabolic partial integro-differential equations[J]. IMA J.Numer,.Anal, 2010(30): 248～276.

[9] W. Mclean, V. Thomée.Numerical solution via laplace transforms of a fractional order evolution equation[J]. J. integr. Equ. Appl, 2009(22): 57～94

[10] W. Mclean, V. Thomée.Maximum-norm error analysis of a numerical solution via laplace transforms and quadrature of a fractional-order evolution eqution[J]. IMA. J. Numer. Anal, 2010(30): 208～230

[11] J. E. Dendy.An analysis of some Galerkin schemes for the solution of nonlinear time dependent problems[J]. SIAM J. Numer. Anal, 1975(12): 541～565

Application of Alternating Direction Galerkin Method in Partial Integral Differential Equation

WANG Jia, LI Li-mei, WANG Yi, WANG Yi-fen, OU Yang-xin
(College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006,China)

Alternating direction implicit Galerkin method are formulated for the two-dimensional partial intergro-differential equations with a weakly singular kernel. These techniques are based on the finite element method in space and the backward Euler in time in combination with order one convolution quadrature approximating the integral term. The method has not only less storage and low computational characteristics, but also has high precision characteristics with finite element method.

partial intergro-differential equations; alternating direction implicit method; backward Euler method; finite element method

O241.8

: A

: 1672-5298(2015)04-0015-05

2015-10-02

湖南省大学生研究性学习和创新性实验计划项目(湘教通[2014]248号)

王 佳(1995− ), 男, 湖南衡南人, 湖南理工学院数学学院2012级本科生. 主要研究方向: 计算数学