基于多级EEMD和WVD分布的谐波/间谐波检测方法

张宇辉，段伟润，李天云

(东北电力大学电气工程学院，吉林省吉林市132012)

基于多级EEMD和WVD分布的谐波/间谐波检测方法

张宇辉，段伟润，李天云

(东北电力大学电气工程学院，吉林省吉林市132012)

为了有效抑制多种噪声和准确检测谐波/间谐波频率，提出了基于多级集合经验模态分解(EEMD)和Wigner-Ville分布(WVD)的谐波/间谐波检测方法。利用白噪声的幅值可调性，对含有噪声的检测信号进行多级EEMD分解，平滑脉冲干扰和削弱白噪声的同时，得到了一组固有模态函数(IMF)分量，对每个IMF进行WVD计算，可准确检测出谐波/间谐波频率，有效抑制了交叉项和噪声干扰。采用最小二乘算法估计各频率分量的幅值，实现了噪声背景下的谐波和间谐波检测。仿真结果验证了该方法的可行性与有效性。

谐波;间谐波;消噪;Wigner-Ville分布;多级集合经验模态分解;交叉项;最小二乘

1 引言

随着非线性负荷的大量使用，电能质量污染日益严重，谐波和间谐波的同时存在，增大了检测的难度。

国内外学者对电网谐波检测问题做了大量的研究工作。快速傅里叶变换(Fast Fourier Transform，FFT)法在非同步采样情况下存在较大的误差，无法精确地检测间谐波的信息［1］。小波变换［2-3］法存在着频率混叠和小波基选取等问题。Prony法［4］虽然可准确估计间谐波的频率、幅值，但其抗干扰性较差。支持向量机的稳健频谱估计方法［5］，采用迭代变权最小二乘法减少了计算复杂度，检测精度高，但需要模型的先验知识。Wigner-Ville分布(WVD)凭借其优良的数学性质而得到了广泛应用，但其交叉项提供了虚假的频谱成分，影响了WVD物理解释［6］。文献［7］采用Hilbert-Huang变换方法［8］(HHT)进行谐波检测，完全根据信号性质自适应进行分解，其核心部分是经验模态分解(Empirical Mode Decomposition，EMD)，但当信号中含有间歇性成分或脉冲干扰等异常事件时，将会产生模态混叠现象，使其IMF的物理意义不明确。为解决EMD模态混叠问题，Wu和Huang提出了集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)方法［9］。

信号中的不同频率分量在时频面上的耦合作用是WVD产生交叉项的主要原因，同时，信号中的噪声也会影响分析结果的正确性。本文将进行多次EEMD分解的操作称为“多级EEMD”，在对含有噪声的谐波和间谐波信号进行多级EEMD分解过程中抑制噪声干扰。通过逐级调节白噪声幅值，使EEMD转换为EMD或逼近EMD，获取质量较高的单一频率固有模态函数(Intrinsic Mode Function，IMF)分量，分别对得到的IMF进行WVD计算，分析结果求和得到抑制交叉项的WVD分布。该方法可实现含脉冲干扰信号中谐波和间谐波频率检测，采用最小二乘算法(LS)获得幅值的估计值，从而实现谐波和间谐波信号频率、幅值的检测。

2 EEMD基本理论

EEMD通过向待分析信号中添加白噪声，改变信号极值点特性，削弱了模态混叠现象。

EEMD方法为:

(1)对待分析信号X(t)加入服从正态分布的白噪声ni(t)，即:

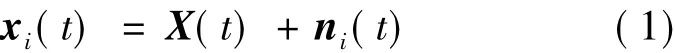
式中，xi(t)为第i次加入白噪声的信号。

(2)对xi(t)进行EMD分解［8］，得到各IMF分量。

(3)重复步骤(1)和(2)共N次，每次添加强度相同但序列不同的白噪声，获得各IMF分量。

(4)对所有N次EMD分解后得到的各层IMF分量分别求整体平均，即为最终的IMF。

(5)待分析信号X(t)可表示为:

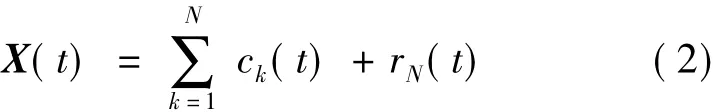
即信号X(t)可表示为一系列固有模态函数ck(t)与一个残余项rN(t)的和。

Huang等人指出白噪声对信号分析的影响有如下统计规律:

式中，e为输入信号与IMF分量重构之后的标准离差;a为白噪声幅值;N为添加白噪声序列的数目。

由式(3)可知:采用EEMD分解时，添加白噪声的幅值a越小，重构精度就越高;当a=0时，EEMD转换为经典EMD。在信噪比较小时，可适当增大a，在补充缺失尺度的同时加快收敛速度。对加入白噪声后的信号进行EMD分解，获取的IMF分量中必然包含随机噪声，选择合适的白噪声添加次数N，可以抑制或消除分解结果中噪声带来的影响。

在EEMD分解过程中，受采样率不足及样条插值的影响，将出现与信号不相关的低频成分，即伪分量。借助IMF与原信号的相关性可以去除其中的伪分量，对于时间序列x1(n)、x2(n)，两者的相关系数定义为:

3 W igner-Ville分布及交叉项

Wigner-Ville分布是一种二次型时频分布，与其他时频分布相比有许多优良性质［10］。信号X(t)的Wigner-Ville分布定义为:

式中，S(t)是信号X(t)的解析信号。

若信号r(t)=u(t)+v(t)，则有

由式(6)可知，两个信号之和的WVD并非每个信号的WVD之和，多出一个交叉项。在待分析信号中含有n个分量时，将会产生n(n－1)/2个交叉项。

4 基于多级EEMD和WVD分布的检测方法

4.1 多级EEMD的提出

在非线性负荷电流信号由基波、谐波与间谐波分量的线性组合构成时，对其进行WVD计算后，将不可避免产生交叉项，在对应的时频面上产生虚假频率，难以确定原始信号的真实构成成分。从交叉项产生原因出发，若将信号分解为若干单频分量，分别对各分量进行WVD计算，将计算结果求和，即可得到抑制交叉项的WVD分布。

EEMD对待分析信号随机加入白噪声序列，平滑脉冲干扰等异常事件，这种随机性使有些信号成分一级EEMD分解后，个别IMF分量还可能存在模态混叠现象，因此，合理地进行多级EEMD分解就有可能获得质量较高的单频IMF分量。

4.2 检测方法步骤

(1)选择合适的噪声强度和重复次数，对含有脉冲干扰的谐波和间谐波信号进行多级EEMD分解，得到一组质量较高的单频IMF。

(2)对步骤(1)得到的IMF分别进行WVD计算，将各分量的计算结果求和，即可得到抑制交叉项的信号WVD分布，达到谐波和间谐波频率检测的目的。

(3)采用LS估计谐波和间谐波分量的幅值。

5 仿真分析

5.1 间谐波信号的数值仿真

原始信号假设为:

采样频率为2kHz，向其中加入3个幅值为－1A、－1A、+1A的脉冲干扰和5%的随机噪声。对上述信号进行一级EEMD分解，各IMF分量和原信号相关系数如表1所示，设置阈值为相关系数序列中最大值的3/5。

表1 各IMF分量与原信号相关系数1Tab．1 Correlation coefficient1 of IMF and signal

此时，阈值为0.3061，保留前5层IMF分量，分别对各IMF进行WVD计算，分析结果如图1所示，可以看出210Hz和400Hz之间出现了虚假频率成分，有必要进行二级EEMD处理，阈值设置同上。

图1 一级EEMD分解的Wigner-Ville分布1Fig．1 WVD 1 of signal based on first level EEMD

图2为经过二级EEMD处理后的WVD，可以看出虚假频率成分已被削弱，谐波、间谐波频率及幅值计算结果如表2所示。

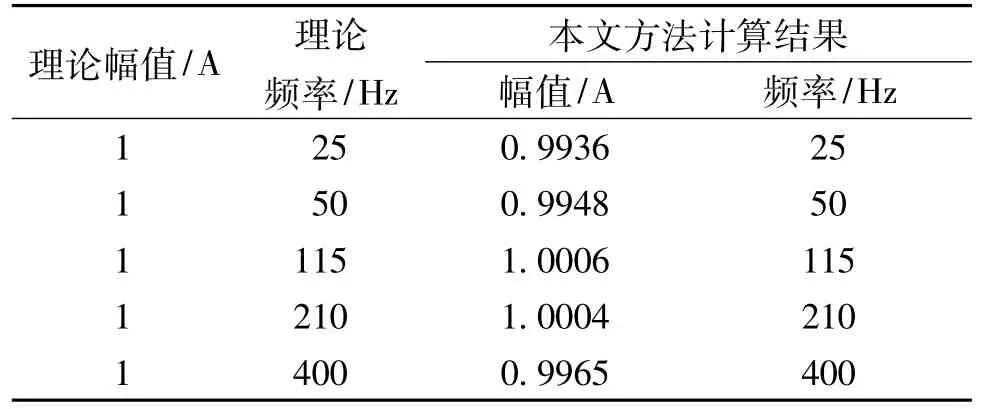
表2 频率及幅值计算结果1Tab．2 Calculation results 1 of frequency and amplitude

图2 二级EEMD分解的Wigner-Ville分布1Fig．2 WVD 1 of signal based on second level EEMD

作为对比，采用基于EMD抑制WVD交叉项的方法对信号进行分析，分析结果如图3所示。从图3中可以看出，EMD模态混叠使WVD分布图上出现虚假频谱成分，干扰了谐波和间谐波频率检测。

图3 EMD分解的Wigner-Ville分布1Fig．3 WVD 1 of signal based on EMD

通过大量仿真证明，对含有脉冲干扰的谐波和间谐波信号进行两级EEMD分解能够有效抑制交叉项，获得较高的频率检测精度。

5.2 调幅信号仿真

间谐波污染严重的负载电流信号通常具有调幅性，考虑如下信号:

式中，n(t)由3个幅值为－1A、－1A、+1A 的脉冲干扰和方差为0.05的随机噪声组成，采样频率2kHz。

对信号f(t)进行一级EEMD分解，各IMF分量和原信号相关系数如表3所示，相关性阈值处理同5.1节，得到的WVD如图4所示。

表3 各IM F分量与原信号相关系数2Tab．3 Correlation coefficient2 of IMF and signal

图4 一级EEMD分解的Wigner-Ville分布2Fig．4 WVD 2 of signal based on first level EEMD

图5为经过二级EEMD处理后(阈值设置同上)的WVD，可以看出交叉项得到了抑制。受LS算法适用范围的限制，对此调幅信号的幅值没有得到较好的跟踪效果，在此只考虑本文方法对频率的检测，结果如表4所示。

图5 二级EEMD分解的Wigner-Ville分布2Fig．5 WVD 2 of signal based on second level EEMD

表4 频率计算结果Tab．4 Calculation results of frequency

采用EMD抑制交叉项的结果如图6所示，从图中无法确定真实信号频率成分。

图6 EMD分解的Wigner-Ville分布2Fig．6 WVD 2 of signal based on EMD

5.3 实例分析

考虑文献［11］的实际电弧炉电流信号，向其中加入5%随机噪声和幅值为25A和－20A的脉冲干扰，波形如图7所示。

图7 电弧炉信号Fig．7 Electric current signal of arc furnace

利用本文方法对含噪电弧炉电流信号进行分析。首先进行一级EEMD分解，各IMF分量和原信号相关系数如表5所示，阈值处理同5.1节，经过一级EEMD分解的WVD如图8所示。

表5 各IM F分量与原信号相关系数3Tab．5 Correlation coefficient3 of IMF and signal

图8 一级EEMD分解的Wigner-Ville分布3Fig．8 WVD 3 of signal based on first level EEMD

图8中，虚假频率与真实频率互相交织，需要进行二级EEMD分解抑制交叉项。分别对IMF2、IMF3、IMF4分量进行EEMD分解，为得到效果较好的WVD，阈值取为0.95，经过二级EEMD处理后的WVD如图9所示，可以看出交叉项已被削弱，谐波、间谐波频率及幅值计算结果如表6所示。

表6 频率及幅值计算结果2Tab．6 Calculation results 2 of frequency and amplitude

图9 二级EEMD分解的Wigner-Ville分布3Fig．9 WVD 3 of signal based on second level EEMD

采用EMD抑制交叉项的结果如图10所示。

图10 EMD分解的Wigner-Ville分布3Fig．10 WVD 3 of signal based on EMD

6 结论

(1)仿真结果表明，基于多级EEMD和WVD分布的谐波和间谐波检测方法，能准确检测出信号中的谐波和间谐波成分。与基于EMD的WVD方法相比较，本文的方法有效地解决了脉冲干扰带来的模态混叠问题。

(2)针对含有噪声干扰的谐波和间谐波信号，本文方法无需预处理，在多级EEMD分解过程中平滑脉冲干扰和削弱白噪声。通过逐级调节白噪声幅值，使EEMD向EMD过渡，利用EMD(或近似EMD)良好的分频特性，获得一组质量较高的单频IMF，既解决了WVD交叉项问题又准确地检测出谐波和间谐波的频率，为谐波检测提供了一种新方法。

［1］张伏生，耿中行，葛耀中(Zhang Fusheng，Geng Zhongxing，Ge Yaozhong)．电力系统谐波分析的高精度FFT算法(FFT algorithm with high accuracy for harmonic analysis in power system)［J］．中国电机工程学报(Proceedings of the CSEE)，1999，19(3):63-66．

［2］黄文清，戴瑜兴，全慧敏(Huang Wenqing，Dai Yuxing，Quan Huimin)．基于Daubechies小波的谐波分析算法(Harmonic estimation method based on Daubechies wavelet)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2006，21(6):45-53．

［3］周龙华，付青，余世杰，等(Zhou Longhua，Fu Qing，Yu Shijie，et al．)．基于小波变换的谐波检测技术(Harmonic detection based on wavelet transform)［J］．电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2010，22(1):80-85．

［4］Lobos T，Leonowicz Z，Rezmer J，et al．High-resolution spectrum estimation methods for signal analysis in power systems［J］．IEEE Transactions on Instrumentation and Measurement，2006，55(1):219-225．

［5］占勇，丁屹峰，程浩忠，等(Zhan Yong，Ding Yifeng，Cheng Haozhong，et al．)．电力系统谐波分析的稳健支持向量机方法研究(A robust support vector algorithm for harmonics analysis of electric power system)［J］．中国电机工程学报(Proceedings of the CSEE)，2004，24 (12):43-47．

［6］乐叶青，徐政(Le Yeqing，Xu Zheng)．平滑伪Wigner-Ville分布在电力系统谐波和电压变动检测中的应用(Application of smoothed pseudo Wigner-Ville distribution in detecting harmonics and short duration voltage variations)［J］．继电器(Relay)，2006，34(16): 39-43．

［7］苏玉香，刘志刚，李科亮，等(Su Yuxiang，Liu Zhigang，Li Keliang，et al．)．Hilbert-Huang变换在电气化铁路谐波检测中的应用(Application of Hilbert-Huang transform in harmonic detection of electrified railway)［J］．电网技术(Power System Technology)，2008，32(18):30-35．

［8］Huang N E，Shen Z，Long S R，et al．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］．Proceedings of the Royal Society of London:Series A，1998，454:903-995．

［9］Wu Z H，Huang N E．Ensemble empiricalmode decomposition:a noise assisted data analysismethod［J］．Advances in Adaptive Data Analysis，2009，1(1):1-41．

［10］张贤达，保铮(Zhang Xianda，Bao Zheng)．非平稳信号分析与处理(The non-stationary signal analysis and processing)［M］．北京:国防工业出版社(Beijing: National Defence Industry Press)，1998．

［11］Zbigniwe L，Tadeusz L，Jacek R．Advanced spectrum estimation methods for signal analysis in power electronics［J］．IEEE Transactions on Industrial Electronics，2003，50(3):514-519．

M ethod to detect harmonics and inter-harmonics based on multiple-level EEMD and W igner-Ville distribution

ZHANG Yu-hui，DUANWei-run，LITian-yun
(School of Electrical Engineering，Northeast Dianli University，Jilin 132012，China)

In order to effectively suppress noise and detect the parameters of harmonics and inter-harmonics，amultiple-level ensemble empiricalmode decomposition(EEMD)and Wigner-Ville distribution(WVD)based method to detect harmonics and inter-harmonics is proposed．Using adjustable white noise amplitude，the intrinsic mode function(IMF)is gained by multiple-level EEMD．It can effectively suppress pulse interference and white noise and accurately detect the harmonics and inter-harmonics signals frequency byWVD of each IMF，and then the least squaremethod is applied to estimate the amplitude of signals，thus the detection of harmonics and inter-harmonics under noises background is implemented．Simulation results show the feasibility and effectiveness of themethod．

harmonic;inter-harmonic;de-noising;Wigner-Ville distribution;multiple-level ensemble empirical mode decomposition;cross-terms;least squares

TM714

A

1003-3076(2015)03-0066-06

2013-07-15

张宇辉(1962-)，男，吉林籍，副教授，硕士，研究方向为自动控制理论、信号处理在电力系统中的应用;段伟润(1987-)，男，黑龙江籍，硕士研究生，研究方向为电力系统中的非平稳工程信号处理。