颅内电极定位中的Zernike矩快速算法研究

刘思伟，董硕，严汉民

首都医科大学宣武医院 医学工程处，北京 100053

颅内电极定位中的Zernike矩快速算法研究

刘思伟，董硕，严汉民

首都医科大学宣武医院 医学工程处，北京 100053

目的 减少颅内电极定位中多模图像Zernike矩的配准耗时，提升其配准精度。方法 用几何中心法和Hough变换法对人脑CT和MRI图像进行几何参数和配准区域的计算，并根据人脑结构特点建立模型对算法有效性进行测试。本文分别应用骨架算法、颅骨提取法、腐蚀联合大津阈值法、边缘增强法、边缘增强联合腐蚀法、Bottom hat法、Sobel边缘提取法对人脑CT和MRI图像进行预处理。结果 对于模型图像，Hough变换法和几何中心法测得的质心与实际质心坐标分别相差±1个像素和±5个像素，主轴误差范围均＜3%。对于CT和MRI图像，几何中心法的计算结果更优，其质心点和主轴的计算误差范围分别可控制在周围5邻域内和±6%内。结论 几何中心法和Hough变换法均能够很好地计算出模型图像几何参数和配准区域。对于CT和MRI图像，几何中心法的计算效果较好，Hough变换法的计算效果有待提升。

几何中心法；Hough变换法；多模图像配准；颅内电极定位；Zernike矩

癫痫是由多种病因引起的慢性脑部疾患，每年新发病人约30万。其中约20%的病人不能采用药物控制，而在这些病人之中，约50%的人可以采用手术治疗，而致痫灶的准确定位是手术成功的关键[1]。颅内电极脑电记录法具有灵敏度高、定位精确的优点，可以对致痫灶进行准确定位。但含有颅内电极的CT图像由于存在金属伪影和金属电极信息，因此与MRI图像的配准效果欠佳，最终影响致痫灶的定位[2]。

近年来，Zernike矩的方法在医学图像配准领域得到广泛应用，其具有特征相关性小、冗余性小、抗噪能力强等特点[3-4]。通过改进有关矩的数学特性，Zernike矩的方法已经能够达到亚像素级的配准效果[5]。

在实际应用Zernike矩的方法对图像进行配准时，常遇到数据量巨大、计算时间过长等问题，且该矩要求待处理数据全部需在单位圆内。基于此，本研究通过应用几何中心法和Hough变换法来提取图像的特征，以获取待配准的两幅图像各自的几何中心坐标和配准区域，以缩小Zernike矩在计算最佳平移参数和伸缩比例时的计算范围，寻找最佳单位圆范围，从而减小计算耗时，提升配准效果。

1 研究方法

1.1 算法原理

几何中心法是数学领域里描述形状特征的方法。本研究将图像特征区域的质心定义为几何中心，以几何中心为圆心所构成的圆形区域为配准区域。在计算时采用加权法和非加权法两种方法来获取质心，之后以该质心为圆心，计算特征半径，以得到配准区域[6-7]。

Hough变换法利用图像的全局特征直接检测目标轮廓，在预先了解区域大致形状的基础上，在图像中寻找预期的形状，因此可以作为简单的模板匹配技术对图像对象进行识别[8]。Hough变换的主要优点是受噪声影响较小，测得结果为依概率分布的函数。本文选取的两幅待配准图像均为人脑图像，而人脑颅骨可以粗略认为其近似圆形，符合Hough变换的适用条件[9]。

为验证上述算法的有效性，本文建立了如下模型进行测试：分别采用单个、双个和3个正圆圆环组合成的近似同心圆和非近似同心圆的两组图像模拟人脑（图1）。人脑图像可以近似成是由颅骨和脑组织这两个质心近似相同的圆环组成的，但对于脑部放有电极的患者而言，由于电极分布无序，且其与颅骨在CT图像上的灰度值基本相近，因此在用灰度信息计算质心时可能会造成颅骨与脑组织的质心不再重合，即颅骨和脑组织变为圆心不同的圆环，故本研究设计了上述两组图像对算法进行测试。与此同时，为了更好地模拟人脑，本研究对两组图像还做了灰度值设定。

图1 模型图像

1.2 处理方法

由于Hough变换计算耗时较大，因此本研究使用该方法测试模型图像时，先利用边缘检测算子对图像进行边缘提取，再根据几何中心法得到的结果设定Hough变换计算范围，以减少计算耗时[10]。

考虑到图像噪声对算法的影响，本研究在应用几何中心法和Hough变换法对CT和MRI图像进行计算前对相关图像进行了预处理。使用几何中心法对MRI图像进行计算的步骤如下：① 采用大津阈值对原始图像进行分割；② 使用腐蚀算法对分割结果进行腐蚀；③ 分别利用有无灰度加权的方法计算图像质心；④ 根据相邻的4邻域对图像进行内部点消除；⑤ 以几何中心点为圆心计算图像配准区域特征半径。使用几何中心法对CT图像进行计算的步骤如下：① 采用大津阈值对原始图像进行分割；② 使用腐蚀算法对分割结果进行腐蚀；③ 分别采用有无灰度加权的方法计算图像质心；④ 对步骤②得到的图像继续进行腐蚀、内部点消除和孤立点消除；⑤ 分别采用Bottom hat、边缘增强、边缘增强联合腐蚀的方法处理图像；⑥ 以几何中心点为圆心计算图像配准区域特征半径。

但在预实验中，上述方法对图像质心的计算效果并不理想，因此对其进行了如下改进：① 提取原始图像中的颅骨和金属电极；② 使用剪影法去除原始图像中的颅骨和金属电极信息；③ 利用大津阈值对剪影图像进行分割并计算几何中心；④ 分别采用Bottom hat、边缘增强、边缘增强联合腐蚀的方法计算半径。

本研究在应用Hough变换法计算CT与MRI图像的几何特征时，利用几何中心法所得的质心为圆心、所得半径的不同倍数为半径，构建同心圆环，两圆之间的区域为计算使用区域[11]，此设计可以在保证计算准确性的基础上减小计算量。对于Hough变换使用的CT和MRI数据，本研究在几何中心法处理的基础上分别进行了以下4种处理：① 提取图像的颅骨部分作为输入数据；② 进行腐蚀和大津阈值处理后作为输入数据；③ 用Sobel边缘提取法处理后作为输入数据；④ 用骨架算法处理后作为输入数据。

考虑到CT和MRI图像中的伪影和部分噪声的灰度值与颅骨的灰度值相同或相近[12]，且在空间上相互连接，因此本研究在提取颅骨信息时也会涵盖上述信息。

2 结果

2.1 实验数据

本研究的原始数据包括头颅CT扫描图像和头颅MRI扫描图像。其中头颅CT图像数据为：植入电极后的CT扫描断层图像，共227层，单幅图像512像素×512像素，像素大小0.5 mm×0.5 mm，层厚1 mm。头颅MRI扫描图像数据为：植入电极前的轴位T1W1像，共268层，单幅图像512像素×512像素，像素大小0.5 mm×0.5 mm，层厚1 mm。原始图像均为DICOM格式数据集，由首都医科大学宣武医院提供。图2为原始图像示例。

图2 CT、MR I原始图像（左图为植入电极后的CT图像，右图为植入电极前的MR I图像）

本研究将模型图像分为两组，每组又分为各个圆环灰度值均相同的和均不同的两组数据，灰度值各异组的灰度值从外到内设定为64、32、16，两组模型图像的最外层圆环的圆心坐标和半径均分别为[194,234]和156 Pixel。

2.2 测试结果

本研究利用MATLAB2007a进行程序编写和结果测试。Hough变换法以几何中心法所得的圆心为圆心、所得半径的1.02倍为半径，构建计算区域；并在原图上绘制出经计算得到的配准区域和质心，以便对两种算法的计算结果进行比较。

图3和表1为模型图像几何中心法的测试结果。图4和表2为模型图像Hough变换法的测试结果。图5和表3为应用几何中心法对MRI图像进行计算的结果。图6和表4为应用几何中心法对CT图像进行计算的结果。图7和表5为使用Hough变换法对CT和MRI图像进行计算的结果。

图3 模型图像几何中心法测试结果

图4 模型图像Hough变换法测试结果

图5 MR I图像几何中心法计算结果

图6 CT图像几何中心法计算结果

图7 CT和MR I图像Hough变换法计算结果

3 讨论

本研究以在包含颅脑全部信息的基础上所得到的配准区域最小的几何参数和配准区域为最优结果。对于质心相同或半径相同的情况，以配准区域小或覆盖噪声区域小为更优结果。

由图3和表1可知，几何中心法对于同组图像中双圆环或三圆环的识别准确率，有灰度加权的结果优于没有灰度加权的结果；对于同组图像，圆环数量越少，计算结果越准确，且近似同心圆组的准确率优于非同心圆组；单圆环图像的测试结果均较好，与是否有灰度加权无关。

由图4和表2可知，Hough变换法对于近似同心圆组和非同心圆组均有较好的识别准确率，且不受圆环数量的影响；对于同一组圆环而言，圆环数量的差异几乎不影响计算结果。因此，该方法对于模型图像的测试结果要好于几何中心法。与此同时，由于Hough变换法在计算中并不涉及灰度信息，因此不需要根据灰度信息进行分组测试。由图4还可知，Hough变换法得到的半径并非为最外层圆环的外半径，而是其内半径。因此对于颅脑图像而言，该方法可能无法得到颅脑最外层组织结构所对应的圆环半径，这点在实际应用时应注意。由于Hough变换法识别圆形的计算结果实际上是圆心和半径的依概率分布，对于以矩阵形式存储的圆形，由于其边缘无法绝对光滑，所以计算出的概率最大值可能并非连续域理论上的概率最大值。

表1 模型图像几何中心法测量结果

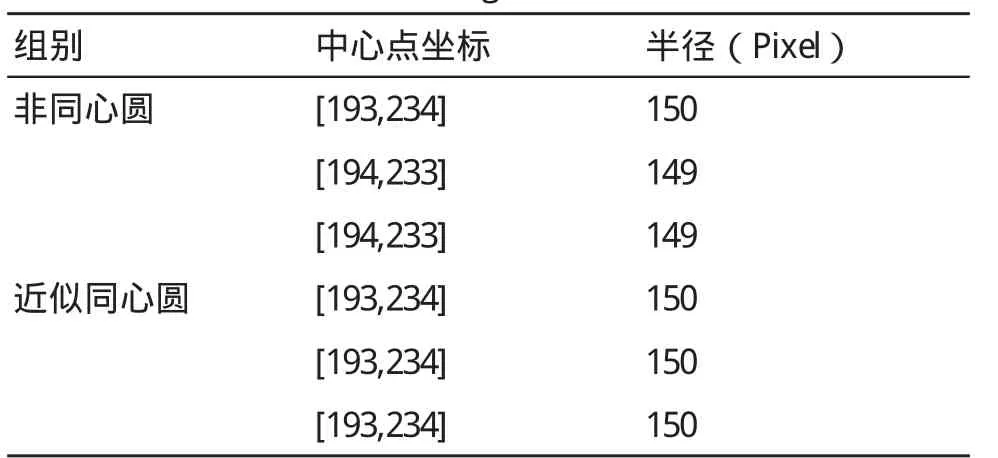
表2 模型图像Hough变换法测量结果

表3 MR I图像几何中心法计算结果

表4 CT图像几何中心法计算结果

表5 CT和MR I图像Hough变换法计算结果

由图5和表3的几何中心法计算结果可以看出，对于MRI图像，加入腐蚀的结果好于未加入腐蚀的结果，未使用灰度加权的结果好于使用灰度加权的结果，带有腐蚀且未加入灰度加权的方法可以较好地计算出MRI中颅脑的几何中心和配准区域。加入腐蚀的算法降低了颅骨外脂肪组织对计算的影响，因而其计算效果提升。而就灰度加权方法对结果的影响来看，模型图像测试结果与真实图像计算结果得出的结论相反，出现这种结果的原因是人脑颅骨并非为标准正圆且在CT图像中的灰度值很大，因此较大的权重值和自身形状反而成了影响测试结果的因素。

由图6和表4的几何中心法计算结果可以看出，对于CT图像，在未去除金属电极影响的情况下，测得的几何中心应偏靠金属电极集中的位置。该方法计算的配准区域和理想范围相比偏靠电极集中且噪声灰度值高的方向，因此会造成相反方向区域信息的丢失，其中采用边缘增强联合腐蚀方法处理的结果该现象最为明显。3种方法计算出的配准区域基本准确，Bottom hat的效果最好，除右下角颅骨信息部分丢失外，保留了全部颅脑信息且引入的伪影和噪声信息较少。

在去除金属电极和颅骨信息之后，几何中心法可以较好地计算出CT图像的几何中心，但是由于去除了颅骨信息，所以在半径计算上出现了较大偏差。3种半径计算方法中只有边缘增强联合腐蚀的方法能够较好地计算出配准区域，而另外两种算法的计算误差比较大。为此，本研究尝试分别用去除颅骨和金属电极信息的方法计算几何中心点，用Bottom hat、边缘增强、边缘增强联合腐蚀的方法计算未去除颅骨信息的图像半径，即联合应用两种方法。从处理结果可以看出，在联合应用的3种方法里，边缘增强方法计算的颅脑配准区域除金属电极集中方向上有信息少量缺失外，能够包括其他全部颅脑信息。虽然联合应用方法比单纯使用Bottom hat要更多地引入伪影和噪声信息，但是其在保留颅脑信息方面的优势更为突出，能够减少有效信息的损失，综合处理效果更佳。

由图7和表5可以看出，使用Hough变换法计算CT图像与MRI图像的几何中心和半径的效果较差，计算得到的几何中心较理想值有所偏移，半径较理想值偏小。对于CT图像而言，Sobel边缘提取法的计算结果最好，但是在颅骨边缘区域仍有信息缺失，而其他3种方法得到的配准区域颅脑信息缺失更多，相比于几何中心法的最佳提取结果仍有不足；对于MRI图像而言，Sobel边缘提取法和颅骨提取法的效果相对较好，但是得到的配准区域颅脑信息缺失严重，颅骨信息集中区域的颅骨信息大量缺失，并且有小部分脑组织信息缺失，而另外两种方法得到的结果更差，与几何中心法的最佳结果相比有很大差距。分析原因大致有以下几点：① 所使用的Hough程序是按照标准正圆编写的，而实际使用的图像并非为标准正圆，因而会导致识别精度下降；② Hough变换法的计算结果为依概率的函数分布，因此最佳结果可能并非对应概率最大时的函数值；③ 从模型测试图像中可以看出Hough变换法在计算半径时会得到内侧圆的半径值，而不是外侧圆的半径值，因此在CT、MRI图像计算中会出现半径值较小的情况。

4 结论

相比于几何中心法而言，Hough变换法的处理时间较长。对于模型图像而言，这两种方法均能取得较好的效果，并且Hough变换法不受灰度变化和干扰信息影响，在近似同心圆组和非近似同心圆组的图像测试中均能准确识别出最大圆的圆心，且计算结果与真实结果相同；但是在实际测试中，Hough变换法对于CT、MRI图像的识别准确率均不高，计算结果与真实值相差较大，但是几何中心法则能很好地识别出颅脑区域。综合而言，几何中心法的计算结果优于Hough变换法，其质心点和主轴的计算范围分别能控制在周围5邻域内和±6%以内。

与Hough变换法相比，几何中心法对于CT、MRI图像的识别准确率较高，但是考虑到Hough变换法在识别时不受噪声和伪影信息的影响，因而可以对Hough变换法进行改进以提升实际测量精度。除上述实验外，对于CT图像，能否利用金属电极和电极伪影的不对称性进行图像几何特征计算；对于CT、MRI图像，不同的边缘提取方法会如何影响Hough变换法的结果；对于矩和主轴的配准方法，在获得两幅图像几何特征之后如何减小金属电极和电极伪影对配准效果的影响；除空间灰度外，引入时频分析能否得到更好的配准参数，对于这些问题我们也将展开深入研究，以更好地解决颅内电极定位中多模图像配准问题[13]。

[1] 柳渊.颅内电极定位和三维显示方法的研究[D].北京:首都医科大学,2009.

[2] Miller KJ,Makeig S,Hebb AO,et al.Cortical electrode localization from X-rays and simple mapping for electrocorticographic research:the"Location on Cortex"(LOC) package for MATLAB[J]. Journal of Neuroscience Methods,2007,162(1-2):303-308.

[3] Yang Z,Fang T.On the accuracy of image normalization by Zernike moments[J].Image and Vision Computing,2010,28(3):403-413.

[4] 郝敏,麻硕士,侯振杰.Zernike矩的不变性与计算实现[J].内蒙古农业大学学报,2009,30(2):222-225.

[5] Ma Z,Kang B,Lv K,et al.Nonlinear radon transform using Zernike moment for shape analysis[J].Computational and Mathematical Methods in Medicine,2013,2013:1-9.

[6] Sotiras A,Davatzikos C,Paragios N.Deformable medical image registration:a survey[J].IEEE Transactions on Medical Imaging,2013,32(7):1153-1190.

[7] 王炎玲,杜建军,郭新宇.基于力矩主轴和互信息的黄瓜茎切片图像配准[J].中国体视学与图像分析,2013,(2):115-122.

[8] 罗述谦,周果宏.医学图像处理与分析[M].2版.北京:科学出版社,2010.

[9] Hermann E,Bleicken S,Subburaj Y,et al.Automated analysis of giant unilamellar vesicles using circular Hough transformation[J]. Bioinformatics,2014,30(12):1747-1754.

[10] Pauwels R,Jacobs R,Bosmans H,et al.Automated implant segmentation in cone-beam CT using edge detection and particle counting[J].International Journal of Computer Assisted Radiology and Surgery,2014,9(4):733-743.

[11] 卢蓉,范勇,陈念年.一种提取目标图像最小外接矩形的快速算法[J].计算机工程,2010,36(21):178-180.

[12] 王琳婧,张书旭,林生趣,等.基于Viscous Fluid模型的快速CTCBCT图像变形配准算法研究[J].中国医疗设备,2013,28(6): 21-23,33.

[13] Naranjo V,Lloréns R,Alcañiz M,et al.Metal artifact reduction in dental CT images using polar mathematical morphology[J].Computer Methods and Programs in Biomedicine,2011,102(1):64-74.

Research on Fast Algorithm for Zernike Moment in Intracranial Electrode Localization

LIU Si-wei, DONG Shuo, YAN Han-min
Department of Medical Engineering, Xuanwu Hospital, Capital Medical University, Beijing 100053, China

Objective To reduce the registration time and improve the registration accuracy of multimodality images with Zernike moment in intracranial electrode localization. Methods The geometric center method and Hough transform method were used in calculating the geometric parameters and registration areas of CT and MRI images of human brain. The validity of the two methods was tested with simulated models which were constructed according to the structural characteristics of human brain. Various methods including skeleton algorithm, skull extraction method, erode combined with OTSU threshold value method, edge enhancement method, edge enhancement combined with erode method, Bottom hat method and Sobel edge extraction method were used in the preprocessing of CT and MRI images. Results The center-of-mass coordinates of stimulated images measured by geometric center method and Hough transform method are different from real center-of-mass coordinates within ±1 pixel and ±5 pixels, respectively. The principle axis errors of the two methods are less than 3%. The results of relevant parameters of CT and MRI images calculated by geometric center method are better that those of CT and MRI images calculated by Hough transform method. The calculation errors of center-of-mass points and principle axis of CT and MRI images calculated by geometric center method can be controlled within 5 neighborhoods and ±6%, respectively. Conclusion Both geometric center method and Hough transform method can calculate the geometric parameters and registration areas of simulated models. However, the calculation effect of geometric center method is better than that of Hough transform method for the geometric parameters and registration areas of CT and MRI images.

geometric center method; Hough transform method; multimodality image registration; intracranial electrode localization; Zernike moment

R742.1；TH774

A

10.3969/j.issn.1674-1633.2015.01.006

1674-1633(2015)01-0023-05

2014-10-09

国家科技支撑计划项目资助（2011BAI02B02）；国家

自然科学基金项目资助（81372923）。

严汉民，教授，硕士生导师。

作者邮箱：liusw911@hotmail.com