基于小样本的安全第一投资组合优化模型
杨扬 哈明虎


摘要:为了解决小样本情况下安全第一投资组合选择问题,将结构风险最小化原则引入投资组合选择过程中。根据结构风险最小化原则的直接实现,构建了含有范数约束的安全第一投资组合优化模型,并研究了模型参数的选取方法。实验结果验证了本模型的有效性。
关键词:小样本;结构风险最小化原则;投资组合选择;安全第一
中图分类号: F830.91文献标识码:A 文章编号:1005-6378(2015)01-0116-04
DOI:10.3969/j.issn.1005-6378.2015.01.022
一、引言
投资组合选择是现代投资组合理论中一个极其重要的研究方向[1-2]。1952年Markowitz[3]提出了均值-方差投资组合选择模型,奠定了现代投资组合理论的基石,同年,Roy[4]提出了投资组合选择的安全第一(RSF)准则。和均值-方差模型不同,安全第一准则没有将方差作为投资组合风险的度量,而是将灾难事件(即投资组合收益低于某个灾难水平)的发生概率作为风险的度量,旨在选择使灾难事件发生概率最小化的投资组合,换言之,Roy关注的是投资组合的下行风险[5]。受这一思想的启发,学者们开始研究开发基于下行风险度量的投资组合选择模型,如均值-半方差模型[6],条件风险价值模型[7],投资组合表现指数最大化模型[8]等。
虽然RSF准则得到了学者们的高度评价和重视,但是它在投资组合选择的实际应用中存在一定的困难。如在实际的金融市场中,资产收益的真实分布函数通常是未知的,投资者仅能够获得资产收益的历史数据,因而无法准确确定不同投资组合所对应的灾难事件发生的概率,限制了RSF准则的应用。目前学者们通常致力于RSF准则的间接实现,即最小化灾难事件发生概率的上界或近似值[4][9-11]。其中,Haley等[11]采用“频率近似法”,构建了光滑安全第一投资组合选择模型,即使用灾难事件发生的频率近似逼近概率,从而最小化灾难事件发生的频率以实现投资组合的RSF准则。由Glivenko-Cantelli定理可知当样本量趋于无穷时,用经验分布函数估计真实分布函数是可行的[12]。但是,在小样本情况下,采用灾难事件频率最小化方法所得到的最佳投资组合并不一定能保证有小的灾难事件概率。因此,研究在小样本情况下如何实现安全第一的投资组合选择是有意义的。
由Vapnik等[12-13]提出的统计学习理论已成为一套非常完善的解决小样本机器学习问题的理论,这个理论中的结构风险最小化原则是小样本情况下解决机器学习问题的指导性原则,在此基础上给出的支持向量机已成功应用于分类、回归和密度估计等机器学习问题。考虑到结构风险最小化原则处理小样本问题的优越性,本文将其引入投资组合选择中以更好地实现RSF准则。
本文主要内容包括:构建了小样本下的安全第一投资组合优化模型;模型参数的选取问题;利用股票市场中的收益率数据对模型进行实证分析。
二、模型构建
考虑n个股票S1,S2,…,Sn的投资组合问题,假定股票收益率是随机变量,则基于RSF準则的投资组合优化模型为minwR(w)=Pr{(w·R)≤θ},
其中,R=(R1,R2,…,Rn),w∈{w|(w·e)=1},e=(1,1,…,1)是n维单位列向量,f(R)是n个股票收益率的联合分布函数。实际上,上述模型还可以表述为如下风险泛函最小化问题
minwR(w)=∫Q(R,w)df(R),(1)
其中,Q=(R,w)=0,(w·R)>θ,
1,其他。
即,小样本情况下的安全第一投资组合选择问题可以归结为小样本下的风险泛函最小化问题,因而可以将结构风险最小化原则[12]引入投资组合选择问题中。由结构风险最小化原则可知,为了最小化实际风险,只需最小化经验风险与置信范围之和。这里,采用结构风险最小化原则的直接实现方法[14]来实现安全第一投资组合选择。
首先选取依赖于参数的决策函数候选集。
F(t)={f=(w·R)|‖w‖2≤t,(w·e)=1},t∈(0,+∞]。
然后求解一系列依赖于参数的最优化问题。
minwRemp[ 瘙 楋 ]=1T∑Ti=1exp-exp[(w·Ri)-θh]
st.(w·e)=1,
‖w‖2≤t,(2)
其中,t∈(0,+∞]。优化问题(2)的解表示为wNC。
最后选择最佳的参数所对应投资组合为最佳的投资组合。
注意到当t2=1/n,由于(w·e)=1,可知优化问题 (2) 的解为wNC=1/n,即基于结构风险最小化原则的安全第一投资组合束退化为均衡投资。当t=+∞时,优化问题(2)退化为光滑安全第一投资组合选择模型。显然,优化问题(2)的解wNC是参数t的函数,参数t的选择对优化问题 (2) 的解wNC有较大影响。
河北大学学报(哲学社会科学版)2015年第1期三、模型参数选取
由前面的讨论知参数t的确定至关重要,其影响优化模型(2)的解。然而,参数t的范围为t∈(0,+∞],增加了选取最佳参数t的难度。接下来,为了提高参数t的选取效率,我们进一步缩小了参数的可选范围。
定理1. 范数约束优化模型 (2) 中参数t的范围t∈(0,+∞]可以缩小为闭区间[1/n,‖wSM‖2],其中wSM为光滑安全第一投资组合选择模型的解。
由结构风险最小化原则的直接实现,需要从有效范围[1/n,‖wSM‖2]内得到最佳的参数。不难看出,当t=1/n时,决策函数候选集F(1/n)内只有一个元素(1/n·R);随着t的增加,决策函数候选集F(t)={ 瘙 楋 =(w·R)|‖w‖2}≤t,(w,e)=1}的元素在增加。即,如果t1≤t2,我们有F(t1)F(t2)。随着决策函数候选集的扩大,优化问题(2)的最优值
1T∑Ti=1exp-exp[(wNC·Ri)-θh]
在逐渐缩小,即经验风险越来越小,直至t=‖wSM‖2,经验风险取得最小值。而t=1/n时,经验风险最大。因此,我们可以得出如下结论,随着参数t的增加,投资组合的经验风险在减小。当样本量很小时,我们知道经验风险最小化并不能保证有小的实际风险,所以我们可以选取较小t的代入优化模型(2);当样本量很大时,通过经验风险最小化得到的投资组合也会有小的实际风险,因而我们可以选取较大的代入优化模型(2);当样本量居中时,我们可以选取闭区间[1/n,‖wSM‖2]内近似居中的点,如
t=1/n+β10‖wSM‖2-1/n,β=4,5,6。
确定最佳参数后,代入优化模型(2),可以实现小样本情况下的安全第一投资组合选择。
四、数值实验
结合结构风险最小化原则及其直接实现,本文提出了用以解决小样本投资组合选择问题的范数约束优化模型(2)。而Haley等[11]提出光滑安全第一投资组合选择模型是在经验风险最小化原则基础上建立的。为了说明本文提出的范数约束优化模型的优越性,将其与光滑安全第一投资组合选择模型进行比较。选择Haley等[11]使用的股票市场数据集作为实验对象,此数据集含有21支股票从1977年1月至1996年12月的240个月收益率样本数据。
采用滚动时域方法:选取训练样本量为T=10,15,…,160的样本Rτ-T,Rτ-(T-1),…,Rτ-1训练模型,得到两个投资组合选择模型的解wSM和wNC,之后分别将所得的最优投资组合应用于第τ个样本Rτ以测试它的表现,即考察所得最优投资组合是否能使(Rτ·w)>θ,其中161≤τ≤240。可以看出我们所选取的测试样本集是不变的,为{Rτ|161≤τ≤240|},而训练样本集{Rτ-T,Rτ-(T-1),…,Rτ-1|161≤τ≤240}随着样本量T的变化而变化。令θ=-0.015,h=0.0171,最佳参数t的选取参照如下公式
t=1/n+β10‖wSM‖2-1/n,β∈[0,10]可以看出,当β=0时,t=1/n;当β=10時,t=‖wSM‖2 。这里,为了考察训练样本量和参数t对模型推广能力的影响,选取了不同的训练样本量(T=10,15,…160)及不同的参数
tt=1/n+β10‖wSM‖2-1/n,β=0.5,1,3,5,7,9,
比较了范数约束模型和光滑安全第一投资组合选择模型在测试样本集上的风险水平,比较指标如下
|{τ∶(Rτ·w)≤θ}|80,τ∈(161,162,…,240)
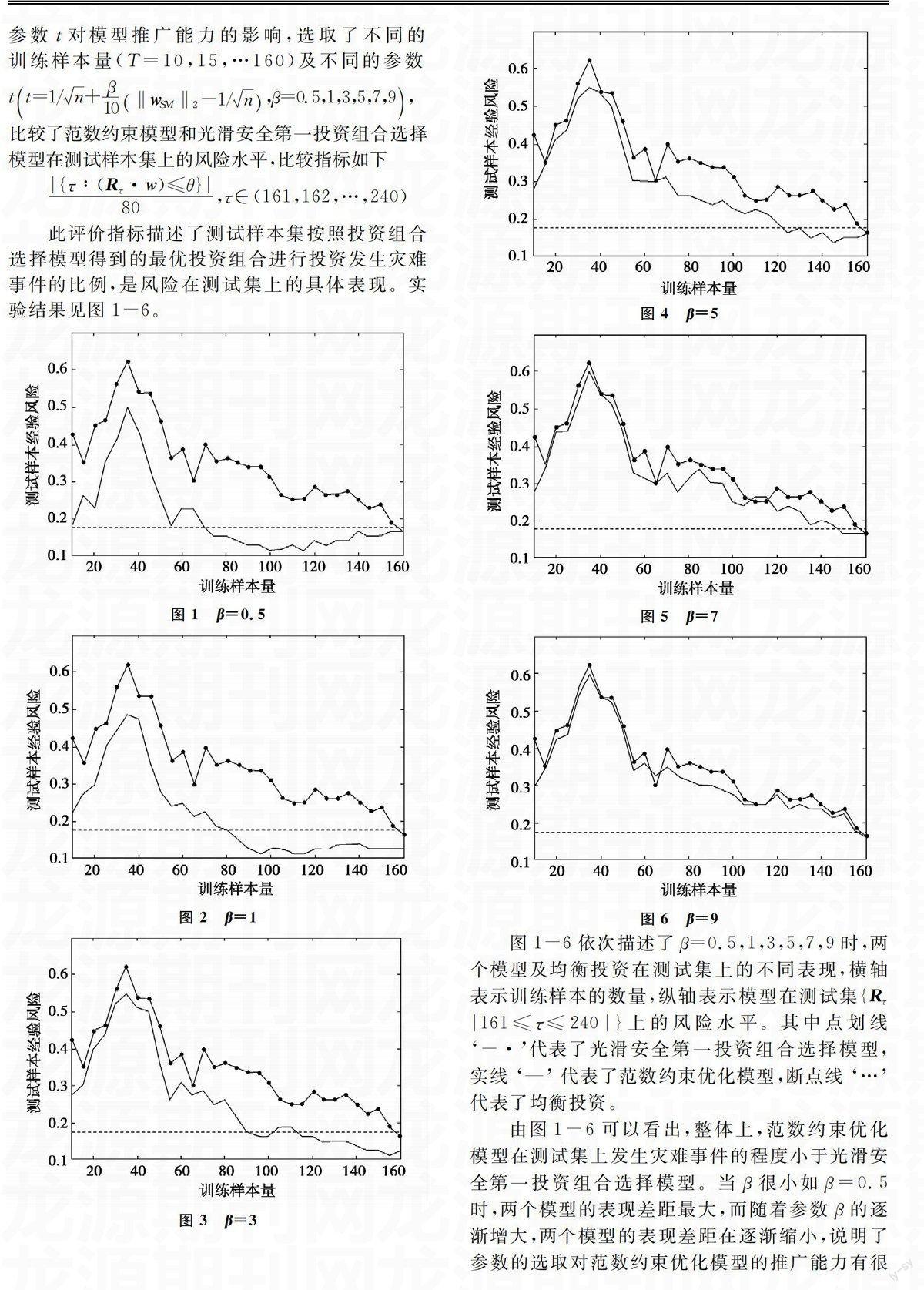
此评价指标描述了测试样本集按照投资组合选择模型得到的最优投资组合进行投资发生灾难事件的比例,是风险在测试集上的具体表现。实验结果见图1-6。
图1-6依次描述了β=0.5,1,3,5,7,9时,两个模型及均衡投资在测试集上的不同表现,横轴表示训练样本的数量,纵轴表示模型在测试集{Rτ|161≤τ≤240|}上的风险水平。其中点划线‘-·代表了光滑安全第一投资组合选择模型,实线 ‘— 代表了范数约束优化模型,断点线 ‘… 代表了均衡投资。
由图1-6可以看出,整体上,范数约束优化模型在测试集上发生灾难事件的程度小于光滑安全第一投资组合选择模型。当β很小如β=0.5时,两个模型的表现差距最大,而随着参数β的逐渐增大,两个模型的表现差距在逐渐缩小,说明了参数的选取对范数约束优化模型的推广能力有很大影响。
此外,当T≥100时,两个模型在测试样本集上的风险水平较低。当T<100时,光滑安全第一投资组合选择模型在测试样本集上的风险水平很高,推广能力较差,而范数约束优化模型的风险水平较低,特别地,当参数t取最小值(即β=0)时,范数约束优化模型退化为均衡投资,其风险水平远远低于光滑安全第一投资组合选择模型。然而,并非参数越小,范数约束优化模型的推广能力越强,如T≥100时,β=1时范数约束优化模型的风险水平比β=0时要低,进一步验证了我们的参数选取原则。
五、结论
本文构建了基于结构风险最小化原则的安全第一投资组合选择模型,有效地解决了小样本下的安全第一投资组合选择问题。初步分析了模型参数对模型推广能力的影响,证明了均衡投资和光滑安全第一投资组合选择模型是本文所构建模型的特例。实验结果验证了本文所构建的模型比光滑安全第一投资组合选择模型具有更强的推广能力。
致谢:本课题来源于国家自然科学基金(No. 61073121;No. 60773062),河北省自然科学基金(No. F2012402037)的部分内容,特此致谢。
[参考文献]
[1]ELTON E J, GRUBER M J, BROWN S J, GOETZMANN W N. Modern portfolio Theory and Investment Analysis[M]. 9th edn. New York: John Wiley & Sons Ltd, 2013.
[2]余维彬. 现代投资组合理论与投资分析[M].7版. 北京: 机械工业出版社, 2008.
[3]MARKOWITZ H M. Portfolio selection [J]. Journal of Finance, 1952, 7(1): 77-91.
[4]ROY A D. Safety first and the holding of assets [J]. Econometrica, 1952, 20(3): 431-449.
[5]CHIU M C, WONG H Y, LI D. Roys safety-first portfolio principle in financial risk management of disastrous events [J]. Risk Analysis, 2012, 32(11): 1856-1872.
[6]MARKOWITZ H M. Portfolio Eelection: Efficient Diversification of Investments [M]. New York: John Wiley & Sons, 1959.
[7]ROCKAFELLAR R T and URYASEV S. Optimization of conditional value-at-risk [J]. Journal of risk, 2000, 2(3): 21-41.
[8]STUTZER M. A portfolio performance index [J]. Financial Analysts Journal, 2000, 56(3): 52-61.
[9]ZABARANKIN M, URYASEV S. Statistical Decision Problems [M]. New York: Springer, 2014.
[10]HALEY M R, WHITEMAN C H. Generalized safety first and a new twist on portfolio performance [J]. Econometric Reviews, 2008, 27(4-6): 457-483.
[11]HALEY M R, PAARSCH H J, WHITEMAN C H. Smoothed safety first and the holding of assets [J]. Quantitative Finance, 2013, 13(2): 167-176.
[12]VAPNIK V N. The Nature of Statistical Learning Theory[M]. 2nd edn. Berlin: Springer, 2000.
[13]VAPNIK V N. Statistical Learning Theory [M]. New York: John Wiley & Sons, 1998.
[14]ZHANG C H, TIAN Y J, DENG N Y. The new interpretation of support vector machines on statistical learning theory [J]. Science in China (Series A: Mathematics), 2010, 53(1): 151-164.
【責任编辑郭玲】

