基于量子遗传模拟退火算法的认知无线电频谱分配方法研究

【摘要】 无线频谱资源的紧张与无线通信应用的激增之间的矛盾越来越突出，认知无线电作为缓解频谱资源紧张的重要途径，其对应的频谱分配方法一直是研究的热点。量子遗传模拟退火算法是将量子遗传算法的多点并行性搜索及模拟退火算法所具有的较强的单点串行搜索能力相融合，模拟退火算法作为一个算子引入到量子遗传算法中能够克服量子遗传算法易产生的“早熟收敛”问题，实现两种算法的优劣互补，该算法在求解优化问题时具有更强的搜索能力和效率，并获得较高质量的最优解。本文将量子遗传模拟退火算法应用于认知无线电频谱分配问题中，采用非合作博弈论模型，研究了多用户竞争多信道的频谱分配方法，通过与已有的基于量子遗传算法的频谱分配性能进行仿真比对，验证了该思路的可行性及优势。

【关键词】 认知无线电 频谱分配 量子遗传模拟退火算法 博弈论 多用户多信道

Researching on spectrum allocation in Cognitive Radio Networks based on Quantum Genetic Simulated Annealing Algorithm

Xiao Chanchan

（CHINA MOBILE （SHENZHEN） LIMITED， Shenzhen， 518048， China）

Abstract： The contradiction between the tension of the wireless spectrum resources and the surge in wireless communication applications is becoming more and more prominent. The spectrum models and algorithms in Cognitive radio network which is an important way to ease the shortage of spectrum resources are always the focus. The integration of the multi-parallel searching capability of Quantum Genetic Algorithm（QGA）and the stronger single-point serial searching capability of Simulated Annealing Algorithm（SA）becomes Quantum Genetic Simulated Annealing Algorithm（QGSA），in which SA is an operator to overcome the premature convergence problem of QGA and complements each other. The algorithm has more powerful searching capabilities and efficiency， and can obtain higher quality solution in solving optimization problem. QGSA is applied to the cognitive radio spectrum allocation in this paper， which is based on non-cooperative game theory model. The spectrum allocation for multi-user and multi-channel is studied. The spectrum allocation performance between QGSA and QGA are compared， and the results verify the superiority of spectrum allocation based on QGSA.

Keywords： Cognitive radio network ， spectrum allocation ， Quantum Genetic Simulated Annealing Algorithm， Game Theory， multiuser multi-channel

一、引言

随着无线通信的应用大量增加，无线终端的数量激增，而且越来越多的移动通信设备和通信服务的融合对更高的数据传输速率的需求日益增加，这造成对无线频谱资源的需求量将达到前所未有的程度。而现实的问题是，无线通信频谱的利用效率并不高。在目前投入运营的无线频段中，存在着许多“频谱空洞”（未被利用的频谱）[1]。

目前，认知无线电频谱分配模型和算法一直是国内外研究热点，既有经典的频谱分配，如图论着色模型、博弈论模型[4][5]、拍卖竞价模型以及干扰温度模型，这些传统的频谱分配算法取得了一定的研究成果，但是也存在诸如时间开销大、系统效用低、频谱利用率低等不足，为此，现已有很多文献陆续提出将量子智能算法应用于认知无线电频谱分配技术中，例如文献[11][12]提出将量子遗传算法应用于认知无线电频谱分配博弈论模型中，并通过仿真实验验证了该算法的优势。文献[13]实现了将量子粒子群算法应用于认知无线电频谱分配中，并与文献[12]中的量子遗传算法频谱分配性能进行了比对，这些研究都验证了量子智能算法应用于认知无线电频谱分配研究的可行性和优势。本文在分析和探讨已存在的基于QGA的认知无线电频谱分配的非合作博弈论模型的基础上[12]，将频谱分配的博弈论思想引入QGSA算法[14]中，提出基于QGSA算法的频谱分配方法。首先通过对频谱分配问题的本质进行分析，给出了两用户和多用户场景下的频谱分配数学模型。其次，针对频谱分配数学模型，给出了采用QGSA算法实现频谱分配的详细流程。最后，对认知无线电网络中基于QGA和QGSA的频谱分配算法进行仿真对比实验，并对仿真对比实验结果进行了分析，从信道数量和用户数量分别对频谱分配结果的影响两方面验证了基于QGSA算法的频谱分配方法的有效性和优越性。

二、频谱分配算法设计

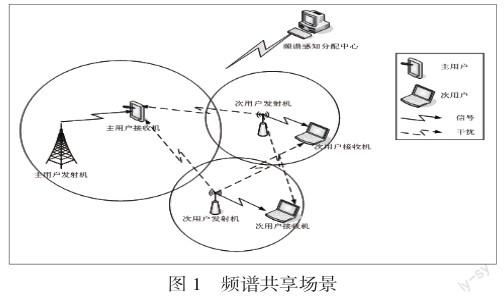
2.1频谱共享场景

在图1中，描述了1个主用户PU和多个次用户SU之间的频谱共享场景。该场景中主用户基站（发射机）通过自身的授权频段发射数据给主用户（接收机），其他的次用户（接收机）对也企图接入该授权频段发射数据，另外主用户也会接收到来自次用户基站（发射机）发射的信号，对主用户来讲，这是干扰信号[7]。在该场景中的频谱感知分配中心可以是一台独立的计算机或者基站，其主要功能是通过感知周围主用户的授权频段的使用情况，实现“频谱空洞”信息的收集，据此采用一定的频谱分配方法来动态地合理分配空闲的频谱资源给这些企图接入的次用户来使用，同时对主用户的通信造成干扰降到最低，达到频谱资源的高效合理的利用。

2.2频谱分配数学模型

2.2.1两用户场景

其中M为用户总数，K为信道总数， Pi j表示第i个用户在信道j上分配的功率。

采用的博弈论模型[13]为：G={M，{Fi，Pi}，{Ii}，{Ci}}，i=1，2，…，M，此博弈包括：

M：用户总数，即为博弈的参与者数量。

Fi，Pi：分别表示用户i的载频集合和各个载频上的分配功率集合，即博弈策略集合。

Ii：用户i获得的各个载频上其他用户带来的干扰信息，即博弈论中的信息。

Ci：用户i的效用函数，此处采用用户i在各个信道上的信道容量和作为效用函数，代表博弈参与者的收益。

根据香农定理C=Blog（1+SIR）可知，设带宽均为B=1，用户i的效用函数为：

通过以上分析可知，频谱分配问题实质上是一个优化问题，可以从全局优化的角度入手，根据其对应的优化问题数学模型，采用QGSA优化算法随机性的进行全局搜索，这也是QGSA算法求解优化问题的核心所在，它能够在随机性的全局搜索过程中自适应地获取搜索空间的信息并掌控搜索方向，以获得优化问题的全局最优解，所以可以采用QGSA实现对频谱分配优化问题的求解。

2.3频谱分配算法流程

1、量子染色体编码。对于一个用户在各个信道上分配的功率值被编码为一个0和1组成的字符串，该字符串代表在该信道上的分配的功率值，所有信道上的0和1组成的字符串代表一条染色体（chromosome），这里采用每个信道的编码长度为10，那么对于K个信道的用户，一条染色体的长度length=10*K。那么将该用户所有信道占用情况编码为一条染色体表示为如图3：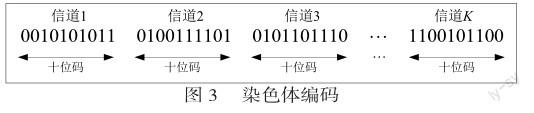

2、参数设置及种群初始化：量子遗传操作的种群规模pop、用户数量M、信道数量K、带内噪声功率N，信道增益hii、hji，每个用户发射功率的最大值Pmax、染色体编码长度length、进化代数maxgen、量子变异概率Pv、转角步长Δθ；模拟退火操作的初始温T、退火系数λ、每一固定温度下的迭代次数为L、更新解的概率Prenew、学习步长step、搜索半径sR。随机生成初始化种群Q（t）。

3、观察测量种群Q（t）的状态：对于任一染色体的任一基因，随即产生一个0～1之间的数，如果该数大于该基因的 2α，则测量结果为1，否则为0，生成二进制解集P（t0）。

4、评估P（t）的效用函数值，两用户两信道的效用函数为式（2.3）。

5、记录P（t）中最佳效用函数值及对应种群中的最佳用户作为下一步种群更新的目标。

6、对当代的种群进行量子交叉、更新和变异，得到子代Q（t+1）。量子交叉：采用全干扰交叉[14]。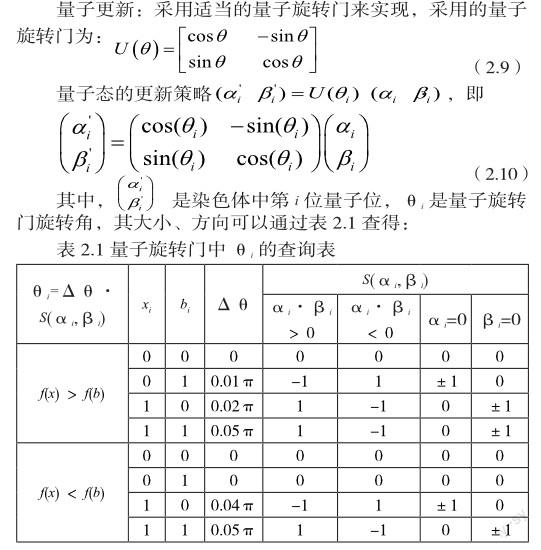

表中xi和bi是当前染色体和当前最优染色体的第i位，f（·）表示适应度函数值，Δθ和S（αi，βi）分别表示θi的大小、方向，即θi=Δθ·S（αi，βi）。

量子变异：通过量子非门实现的，具体操作如下：

1）以某一概率值从当前种群中选择若干个体作为变异对象；

其中jiP→表示由当前状态i向这新状态j的转换接收概率，Δ=f（j）-f（i）表示状态间能级的差值，当能级增量Δ≤0时，接收新状态，否则以某一概率接收新状态。

3）判断当前温度是否足够低，当温度不够低时，继续进行模拟退火操作；当温度足够低，停止模拟退火操作，并记录目前最佳效用函数值及最佳用户，将最佳用户作为下一次种群更新的目标，继续（8）；

8、判断遗传操作是否达到最大进化代数maxgen，若没有达到，继续（6）-（7）；若达到，算法结束。此时搜索到的最优解作为QGSA算法对所有用户进行的频谱分配达到的纳什均衡状态。

三、算法仿真及比较分析

基于QGSA的频谱分配仿真参数设定如下：

量子遗传操作的种群规模pop=60，带内噪声功率N=0.001，信道增益，每个用户发射功率的最大值Pmax=1W、染色体编码长度length=20，进化代数maxgen=300，量子变异概率pm=0.15，转角步长Δθ=0.08π；模拟退火操作时，初始温度T=1000，退火系数λ=0.9，每一固定温度下的迭代次数为L=15，每一固定温度下适应度函数值允许最大连续未改进次数cnt=3，退火算法运行过程中更新解的概率Prenew=0.3，学习步长step=0.2，搜索半径sR=0.1。

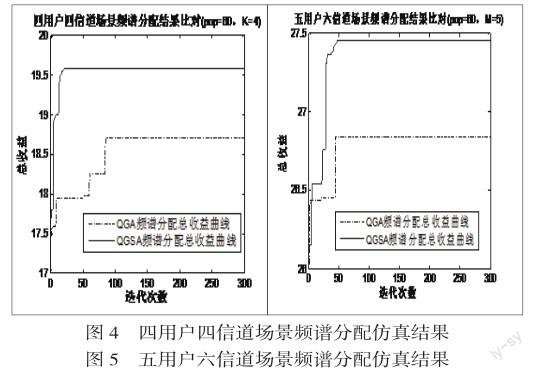
以上仿真结果显示：

QGSA算法在解决该优化问题时的寻优性能优于QGA算法，QGSA算法能够在较短的时间内达到更好的纳什均衡状态，这主要是因为SA算法的引入使得QGSA算法能够跳出局部最优解，这恰恰克服了QGA“早熟收敛”的寻优瓶颈，增强了QGSA的寻优能力，使得QGSA表现出不错的寻优能力，更能有效的解决频谱分配问题。

1、统计分析

在设定QGA和QGSA频谱分配算法各自运行30次，根据得到的实验统计结果数据，从信道数量和用户数量对频谱分配的影响两方面来进行分析：

1）信道数量对频谱分配结果的影响。在相同用户数量情况下，随着信道数量的增加，频谱分配的总收益均呈现增大的趋势，这主要是因为频谱的利用率得到了提升，从而使得整体的信道容量和增加。另外，随着信道数量的增加，QGA和QGSA频谱分配算法的频谱分配性能的差距越来越大，QGSA的频谱分配性能越来越好，这说明在多信道的情况下，QGSA频谱分配算法的优势越明显。

2）用户数量对频谱分配结果的影响。在相同信道数量情况下，随着用户数量的增加，频谱分配的总收益均呈现下降的趋势，这主要是因为用户之间的非合作博弈造成对频谱资源的竞争越发激烈，导致频谱利用率下降，整体的总收益也出现下降趋势。但是，总收益也不会一直递减，从仿真数据来看，随着用户数量的继续增加，总收益的下降趋势趋于平稳。并且，整个的频谱分配结果表明，相比于QGA频谱分配算法，QGSA频谱分配算法受用户数量的影响比较小，整体体现出更好的频谱分配性能。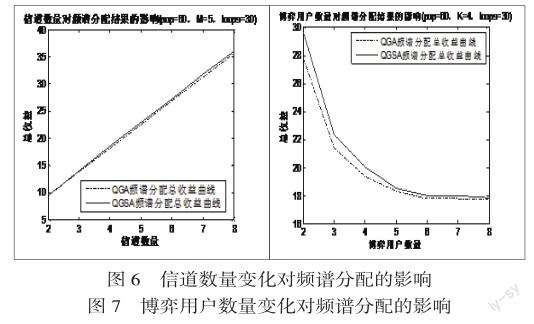

四、结论

本文在探讨两用户和多用户的认知无线电频谱分配问题的非合作博弈数学模型基础上，通过分析频谱分配问题的本质，提出将具有更强搜索能力的量子遗传模拟退火算法应用于求解该问题，并给出了基于QGSA的频谱分配流程，通过仿真实验，将基于QGSA的频谱分配性能与基于QGA的频谱分配性能进行了比对，验证了基于QGSA的频谱分配性能的有效性。另外，根据仿真数据，从用户数量和信道数量对频谱分配性能的影响两个方面分别进行了总结分析。

参 考 文 献

[1]谢显中. 认知无线电技术及其应用[M]. 北京：电子工业出版 社， 2008.

[2] Mitola III J， Maguire Jr G Q. Cognitive radio： making software radios more personal[J]. Personal Communications， IEEE， 1999， 6（4）： 13-18.

[3] Haykin S. Cognitive radio： bra in-empowered wireless communications[J]. Selected Areas in Communications， IEEE Journal on， 2005， 23（2）： 201-220.

[4]曾轲， 李少谦. 基于博弈论的认知无线电频谱分配技术研究 [D][D]. 成都： 电子科技大学， 2007.

[5]张森. 基于博弈认知无线网络动态频谱分配和功率控制研究[D]. 北京邮电大学， 2010.

[6]杨蕊. 认知无线电频谱资源分配与共享技术研究[D]. 哈尔滨工程大学， 2012.

[7] L. Lu， X. Zhou， U. Onunkwo， an d G. Y. Li， “Ten years of research in spectrum sensing and sharing in cognitive radio，”EURASIP J. Wireless Commun. Netw.vol. 28， Jan. 2012 [Online]. Available： http：//jwcn.eurasipjournals.com/content/2012/1/28， [Online]. Available：

[8] Ding L， Melodia T， Batalama S N， et al. Distributed resource allocation in cognitive and cooperative ad hoc networks through joint routing， relay selection and spectrum allocation[J]. Computer Networks， 2015.

[9] Lu L， He D， Yu X， et al. Graph-based robust resource allocation for cognitive radio networks[C]//Acoustics， Speech and Signal Processing （ICASSP）， 2014 IEEE International Conference on. IEEE， 2014： 7298-7302.

[10] Aslam S， Shahid A， Lee K G. Primary user behavior aware spectrum allocation scheme for cognitive radio networks[J]. Computers & Electrical Engineering， 2015， 42： 135-147.

[11]赵知劲， 彭振， 郑仕链， 等. 基于量子遗传算法的认知无线 电频谱分配[J]. 物理学报， 2009， 58（2）： 1358-1363.

[12]朱东坡， 李飞. 量子遗传算法在认知无线电频谱分配中的应用[ J]. 2010 年通信理论与信号处理学术年会论文集， 2010.

[13]丁颖. 量子粒子群算法的改进及其在认知无线电频谱分配中的应用[D].南京邮电大学，2013.

[14]肖婵婵. 认知无线电网络场景下的主用户定位方法研究[D].南 京邮电大学，2014.

[15]李士勇， 李盼池. 量子计算与量子优化算法[M]. 哈尔滨： 哈尔滨工业大学出版社， 2009.