反激开关电源的混沌现象与混沌控制的研究

魏广平　龙素华

摘 要：混沌主要指出现在确定系统中相关“不确定”现象。而这种“不确定”现象往往发生在非线性系统中。其中开关电源作为一种非线性动力学系统，其特点就是非线性现象比较丰富。另外，在有关参数影响下，开关电源就会出现混沌现象。对此，经过对开关电源的混沌现象进行分析和研究，从而更为全面与深入理解开关电源具备的非线性行为。

关键词：反激；开关电源；混沌现象；混沌控制

单端反激式的拓扑结构具有输出稳定、输出波纹小和体积小等特点，因此被大量应用在开关电源相关设计中。对此，从反激式开关电源入手，通过对开关电源相关非线性行为进行研究，制定了混沌有效控制方案，进而可以确保开关电源实现稳定和可靠以及优化运行。

1 应用MATLAB完成数学模型仿真

在研究反激式开关电源离散模型相应混沌现象的过程中，研究方式一般分成定性与定量两类。其中定性分析方式主要依靠状态变量频谱与相图以及分岔等有效观察混沌运行现象。而定量分析方式主要包含了Lyapunov指数的分析方式和功率谱的分析方式以及分形维数的分析方式等。在上述分析方式中，利用分岔图可以清晰的展现出系统处于周期状态下到混沌状态的各个流程。而且在分岔图性方面而言，系统状态一般情况下是由许多有序点构成。在系统从稳定的状态慢慢转换至混沌状态时，其中参数值的变化，可以利用迭代计算方式获取数值点，同时各个数值点并非重合，将各个数值点绘制的坐标图上，就可以充分体现出分岔图。同时敏感参数严重影响着系统的总体运行状态。若是敏感参数在相应的范围之内发生变化，就会充分体现出系混沌状态和周期运行的流程。针对存在混沌问题的非线性系统而言，所有的敏感参数在出现变化时，都会严重影响系统的整体运行状态。可是并非敏感参数的任意排列和组合都造成系统进入混沌状态。同时系统的混沌状态仅仅在对应的敏感参数有限的相关范围之内出现变化。通过上述分析，在电路分析过程中，只可以选取参数可以使系统进入混沌状态之后，调节系统至小范围之内的敏感参数变化。

2 创建反激式开关电源的离散模型

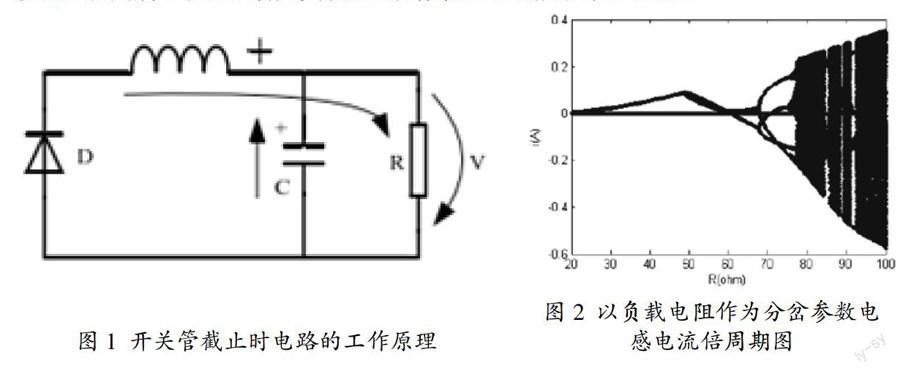
对于反激开关电源而言，高频变压器既是变压器又是储能电感。一般情况下，可以将电路运行过程分成两个流程，然后对各个流程完成分析。其中开关管有效连接后，一直到整流二极管截止，此时的高频变压器就实施能量的储存，同时输出的电眼一般由输出电容提供。当开关管截止后，整流二级管导通，输出电压主要由高频变压器（相当于储能电感）和输出电容提供。该原理如图1所示。

以负载电阻当作分岔参数，获取的图形如图2所示。

在MATLB中，利用迭代计算方式对反击变化器形成的离散映射有关模型进行计算，并且把负载电阻R作为相应分岔参数，该取值的范围是20Ω至100Ω，而迭代步长是0.1Ω。其它相关电路的参数确定是V1=48V，T=100us，L=0.5mH，C=4.7uF，Vref=20V等。把数值的求解结果合理绘画在以负载电阻R作为横坐标、电感电流作为纵坐标的相关坐标平面中，能够获取系统分岔图如图2所示。从图中能够看出，反激变频器通过周期1和周期2以及周期4等，然后进入了混沌状态。若是负载的电阻R处在20Ω至100Ω间发生变化，表明系统处于比较稳定周期里。如果负载电阻数值R为45.2Ω，此种状况下反击变化器就会产生成倍周期分岔，并且系统就会步入周期2状态。另外，若是负载电阻数值R为72.8欧姆，此时反激变换器处在周期4状态。若是负载的电阻数值R逐渐变大，系统最后就会步入混沌状态。

3 反激变换器的混沌控制

3.1 混沌运动的特点

混沌运动状态不仅是非周期的，而且运动轨道也是非周期的。简而言之，对于变量空间而言，混沌吸引子维数通常比周期状态下的吸引子大，而且混沌运动系统中，所有混沌吸引子每一个对到都为各态遍历。此种状况下，混沌可以在对应的混沌吸引子的有关范围之内，合理控制操作和选取控制目标态，进而确保混沌控制方式具备良好的灵活性。其次，混动运动状态相应本质特征主要是对初值存在敏感依赖性，所有相邻的轨道间有关距离会在时间的改变下，通过指数方式变化，从而就造成混沌运动在长期行为下存在不可预见性。对此，在系统中施加相对较小的扰动就能够使系统运动出现较大变化。

3.2 混沌控制方式

首先是OGY控制方式，其为一项参数微扰先进控制行驶，合理利用混沌运动对于小参数扰动敏感依赖性，可以选择便于调节敏感参数完成微扰，同时把相关奇异吸子里存在的不稳定轨道实现稳定，进而使被控系统步入固定的周期状态，实现控制混沌的目标。在设计OGY控制方式的过程中，可是忽视系统相关动力学行为，但必须充分了解系统相图，选择有关试验方法对系统状态变量实现连续测量，并且计算出系统里闪频映射，然后建立“庞加莱”截面，确定系统中相关奇异吸引子。并且在确定混沌吸引子相关不稳定周期轨道基础上，选择一条可以在混沌吸引子中期望不稳定的周期轨道作为控制目标，同时在混沌运动遍历运动至该周期周围时，针对系统此时的状态变量实现微小扰动，就能够把混沌的运动稳定在此周期轨道中。其次，参数共振扰法和外加周期的微扰方法。在混沌控制过程中，这两种方式较为相似，主要为外加周期的微扰信号，其中参数共振的微扰方法一般是干扰动力方程的相应输入源，然而外加周期的微扰方法一般是微扰系统相应敏感性参数。但是都能够将混沌有效抑制，并且使系统转换至期望的周期态。另外，参数共振的微扰方法为一项无反馈型的混沌控制方式，为OGY控制模式中相关改进控制方法。针对敏感参数实现特定频率的微小扰动，可以有效实现系统混沌状态转换至周期运动状态。即参数振动相应扰动模式可以使动力学系统与之前轨道偏离，并且进入周期轨道。若是施加相应频率参数扰动，可以使系统慢慢进入某个周期轨道。因此，科学施加参数扰动能够有效防止系统出现混沌运动，或是消除系统的混沌运动。一般状况下，选取敏感性参数的过程中，选取对系统状态的方程影响相对比较大，便于改变状态变量当作扰动参数。

4 结束语

经过对开关电源的混沌现象进行分析和研究，从而更为全面与深入理解开关电源具备非线性行为，充分应用混沌控制方式，比如说OGY控制方式、参数共振扰法和外加周期的微扰方法等，可以有效确保系统避免或是消除混沌现象。

参考文献

[1]罗晓曙，汪秉宏，等.DC-DC buck变换器的分岔行为及混沌控制研究[J].物理学报，2013，52（1）：11-17.

[2]张波，曲颖.BUCK DC/DC变换器分岔和混沌的精确离散模型及实验研究[J].中国电机工程学报，2013，23（12）：99-103.

[3]张波，曲颖.电压反馈型Boost 变换器DCM的精确离散映射及其分岔和混沌现象[J].电工技术学报，2012，17（3）：43-47.

[4]周宇飞.DC-DC开关变换器的滑模变换结构控制方法及混沌状态研究[D].广州：华南理工大学，2011（10）：12-18.