直线度误差处理模型及算法研究

杨亚辉　赵峰　罗楠

摘 要：文章介绍了直线度误差处理的三种基本数学模型，并比较了现有的直线度误差处理算法，提出直线度误差处理算法的研究方向。

关键词：直线度；误差处理；算法

中图分类号：TP274 文献标识码：A 文章编号：1006-8937（2015）09-0051-03

直线度误差是用来评定长直零件或长直平面机械加工精度的重要指标之一。20世纪80年代，伴随着计算机软硬件技术的迅猛发展，虚拟仪器技术也得到广泛应用。通过搭建软硬件平台将虚拟仪器技术用来检测直线度误差已成为可能，而其中用来处理测量误差的计算机算法又是研究的热点。

1 概 述

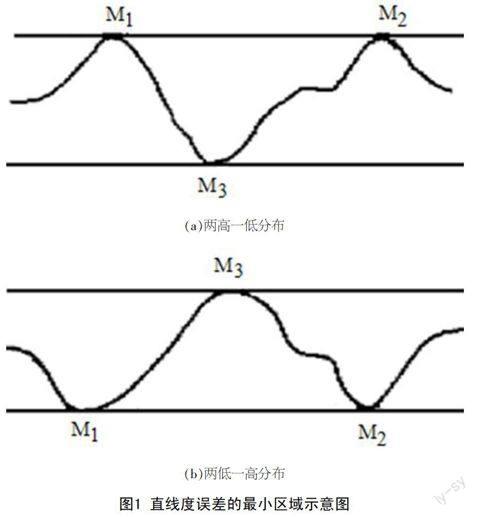
给定平面内的直线度误差区域是由一组平行直线所形成的包容区域，如图1所示，平行直线与被测直线符合相间准则（两高一低或两低一高），其形成的区域即为最小包容区域（简称最小区域），直线度误差用最小区域的宽度来表示。

2 直线度误差处理模型

通过一定的检测方法获得直线度误差测量数据，采用计算机对误差数据处理时，可以有最小包容区域法（最小区域法）、两端点连线法、最小二乘法等三种数据处理模型。在上述数据处理模型中，最小区域法评定的误差结果为最小，并且符合国家标准，常用来仲裁；两端点连线法最为简单，便于手工作图实现，在实际生产中应用广泛，但误差结果最大；最小二乘法便于计算机实现，已在测量仪器中得到应用，误差结果介于最小区域法和两端点连线法之间。

2.1 最小区域法

在采用最小区域法评定直线度误差时，首先构建最小区域评定基准直线LMZ，做两平行直线与基准直线平行，平行直线包容实际直线并且满足相间准则，如图2所示。

2.3 两端点连线法

在采用两端点连线法评定直线度误差时，首先过实际直线首尾两端点连线作为评定基准直线LBE，做两平行直线与基准直线平行，平行直线包容实际直线，如图4所示。

由式（13）求出参数A，B值后，代入式（2）得到最小二乘直线，再由式（4）和式（5）求得误差值。

其算法流程如圖6所示。

3.3 两端点连线法

两端点连线法相对比较简单，与最小二乘法大体相似，由式（10）求得参数A，B值后，再由式（2）、（4）、（7）就可得到直线度误差值，其算法流程图可参照图6。

4 结 语

直线度误差处理应依据最小包容区域法，尤其是在有争议时。各种算法只是讨论了算法的可实现性，未进行算法时间维度和空间维度的计算，算法还应进一步进行优化。

参考文献：

[1] GB/T 11336-2004，直线度误差检测[S].

[2] 周富臣，周鹏飞，张改.机械制造计量检测技术手册[M].北京：机械工业出版社，2000.

[3] 杨亚辉.基于VB的直线度误差数据处理[J].广西轻工业，2008，（9）.