单导体棒在双轨上滑动问题分析

邢洪明 高翔

[摘 要]单导体棒在双轨上滑动问题涉及电磁感应、欧姆定律、运动学及动力学等知识，学生对这类问题进行分析解答时常感到难以下手。由于这类问题涉及的知识点多，且分析难度大，在实际教学中，教师也常易出现顾此失彼的现象。为了便于教师教学、学生学习，本文对单导体棒在磁场中运动问题进行分类分析。

[关键词]有源回路 无源回路 力和运动 功能转换

单导体棒在磁场中切割磁感线产生感应电动势，若回路闭合，则产生感应电流。导体棒在磁场中运动时，因受安培力作用而使导体棒的运动发生变化，同时产生不同形式的功和能之间的转换。从能量转化角度看，一是将其他形式的能转化为导体棒的机械能和闭合回路的焦耳热，二是消耗导体棒的机械能，转为闭合回路的焦耳热。

安培力与磁场强度、电流强度、导体棒的有效切割长度有关。导体棒切割运动速度影响通过导体的电流，进而影响导体棒所受的安培力。但反过来导体棒所受的合外力又影响导体棒的运动速度，在这样的相互制约的作用下，导体棒的运动趋向一种相对稳定的状态。在实际教学中，教师应引导学生分析清楚这一变化过程，这样能有效提高学生的分析能力和解决实际问题的能力。导体棒在磁场中的运动问题可分为导体棒所在回路有源和无源两类，本文从以下几方面作些分析探讨。

一、有源和无源回路对比分析

依据导体棒受力情况来分，我们可将导体棒在双轨上的运动问题分为导体棒受外力和不受外力作用两种情况。

二、实例分析

1.有源和无源回路中导体棒受外力作用对比分析

【例1】 如图1所示，甲图中的电容器C原来不带电，除电阻外，其余导体的电阻均不计，光滑且足够长的导轨水平放置，现给导体棒ab水平向右的初速度v，则甲、乙、丙三种情形下，ab棒最终的运动状态是（   ）。

图1

A.三种情形下导体棒ab最终均做匀速运动

B.甲、丙中导体棒ab最终将以不同的速度做匀速运动，乙中导体棒ab最终静止

C.甲、丙中导体棒ab最终将以相同的速度做匀速运动，乙中导体棒ab最终静止

D.三种情形下导体棒ab最终均静止

【认知困惑点分析】

1.三幅图中导体棒均因平动切割磁感线产生电动势，而消耗导体棒的机械能，消耗的机械能转化为闭合回路的电能。认知困惑点是如何判定图丙中感生电动势和原电源提供电压的叠加关系。

2.图甲是含容电路，电容器两极板之间的绝缘电介质使电路处于断路，但由于导体棒运动速度变化使平动切割产生的电动势不断改变，实现对电容器充电或者放电，形成了充电或者放电电流，电路好像处于“闭合”状态。判断甲图中是否有电流是此问题的难点。

3.导体棒趋向稳态过程中消耗的机械能转化为何种形式的能是求解本题的关键，也是对比分析纯电阻电路和含容电路的重点。

[基金项目] 本文系山东省教学研究十二五重点课题《关于“标准”和认知心理下的有效构建的教学设计研究》（课题编号：zd20130085）阶段性成果。    解析：图甲中ab棒以速度v向右运动，切割磁感线产生动生电动势E=BLv，由右手定则判断Ua>Ub。对电容器充电形成了充电电流i=Δq/Δt，金属棒受到向左的安培力F安=BLΔq/Δt作用，而做减速运动，产生的电动势E=BLv随速度减小而减小，当导体棒产生 的感生电动势与电容的充电电压相等时，电路中没有电流，导体棒也不再受安培力作用，此时，导体棒做匀速直线运动，终态时v从功能角度看 ：充电电流流经闭合回路，使导体棒受安培力作用，消耗的机械能转化为电容器储存的电能和充电电流流经闭合回路时产生的焦耳热。

图乙中，ab棒向右运动切割磁感线，产生动生电动势E=BLv，Ua>Ub。闭合回路产生感应电流I=BLvR+r，导体棒受安培力F安=B2L2vR+r作用，做加速度减小，速度减小的变减速运动，最终停下来。从功能角度讲是消耗的机械能转化为闭合回路的焦耳热。

图丙中，涉及外电源供电和导体棒平动切割产生电动势。因导体棒向左或向右运动的差异而出现正向和反向电动势。对于图示中的向右运动，E总=E外+BLv，导体棒受向后的 F安=BLE+BLvR+r 作用，而做减速运动，直至停下来。在这一过程中消耗的机械能转化为闭合回路焦耳热的一部分（还有电源提供的电能转化为另一部分焦耳热）。电源向外电路供电，导体棒又开始向左做加速运动，当外部电源提供的电压U路=RR+rE 和加速后平动切割产生的反电动势E′=BLv相等时，导体棒以v=RBL（R+r）E做匀速直线运动，所以答案选B。

2.无源回路中导体棒受外力作用问题分析

无源回路中导体棒在导轨上受外力作用，做切割磁感线运动，若回路闭合，则有感应电流，导体棒受F安作用，从而改变导体棒的加速度，关联性制约使得导体棒最终趋向稳定的状态，通过外力做功使得外部其他形式的能量发生转化。

图2 【例2】 如图2所示，两条平行导轨所在平面与水平地面的夹角为θ，间距为L。导轨上端接有一平行板电容器，电容为C。导轨处于匀强磁场中，磁感应强度大小为B，方向垂直于导轨平面。在导轨上放置一质量为m的金属棒，棒可沿导轨下滑，且在下滑过程中保持与导轨垂直并良好接触。已知金属棒与导轨之间的动摩擦因数为μ，重力加速度大小为g，忽略所有电阻。让金属棒从导轨上端由静止开始下滑，求：

（1）电容器极板上积累的电荷量与金属棒速度大小的关系;

（2）金属棒的速度大小随时间变化的关系。

【认知困惑点分析】

1.电容器在电路中“隔直流通交流”，无法组成稳恒直流通路，所以不少学生认为导体棒切割磁感线运动，“有势无流”，故导体棒不受F安作用，只有重力做功，误认为沿光滑轨道做a=gsinθ的匀加速直线运动。

2.没有认清导体棒运动切割产生变化的电动势对电容器持续性充电，形成充电电流这一事实，误将直流电路中I=E/R的计算认定为唯一计算电流的方式，缺少了i=Δq/Δt，致使表征F安时依然用直流电路电流来表征，错误使用F安=B2L2vR+r 计算，结果造成了无法找到电阻R，而出现求解困难。

3.导体棒趋向稳态过程中消耗的机械能向何种形式的能转化，是求解本题的关键，也是对比分析纯电阻电路和含容电路的要点。从本题解析可以看出，导体棒下滑过程中减少的重力势能转化为导体棒的动能、电容器储存的电能和电流产生的焦耳热。

解析：导体棒PQ在重力作用下沿光滑导轨下滑，切割磁感线运动产生电动势，由右手定则判定可知UQ>UP，产生的电动势全部加在电容器两极板上U=E=BLv。

∵C=qU=qBLv，∴q=CBLv

对电容器充电形成充电电流：i=Δq/Δt=CBLv/t

分析导体棒受力可得：mgsinθ-B2L2Ctv-μmgcosθ=mv/t

解得：v=mg（sinθ-μcosθ）m+B2L2Ct

含容电路中因导体棒切割磁感线运动产生变化的电动势，对电容器持续充电形成充电电流，当充电电流流经闭合回路时，导体棒受安培力作用而做负功，这一部分能量转化为电阻的焦耳热。对电容器充电使得电容器储存的电能不断增加，因此导体棒减少的机械能转化为电路的焦耳热和电容器储存的电能。

【引申探究】如果在电容器两端并联一个电阻，电路将成为直流通路和含容电路的充电通路，这也因此使得导体棒减少的机械能转化为闭合回路的焦耳热和电容器的电能，这两种形式能量转化是通过克服安培力做功来实现的。

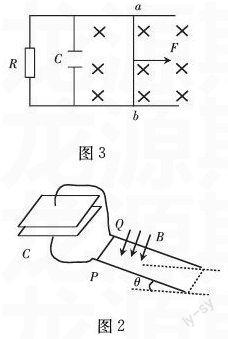
图3 【例3】 如图3所示，在光滑裸导轨的左端接一定值电阻R，在R的右端并联一个电容为C的电容器，导体棒ab在恒力F的作用下向右匀速运动，匀强磁场的磁感应强度大小为B，试判定该导体棒克服安培力所做的功能否等于回路中产生的焦耳热？

解析：导体棒匀速运动产生恒 定的电动势，在由定

值电阻组成的闭合回路中产生的感应电流I=BLv/R， 电流通过电阻时，电流所做的功为Q=I2Rt。

感生电动势加在电容器两端，电容器充电后储存的电场能EC=12CU2=12qU。

导体棒匀速运动时，F=F安=B2L2v/R ，在匀速运动的过程中流经导体棒的电流为I=BLv/R，在电容器充电阶段，导体棒中的电流为iab=（E/R）+i充电，从能量守恒角度讲WF=ΔQ+ΔEC。