木薯叶面积预测模型研究

王祎娜　黄洁　杨重法

摘 要 为探讨木薯叶面积快速准确的非破坏性测定方法，以E25、华南5号、华南6号、华南7号、华南8号、华南9号、华南101、华南124、华南8013共9个木薯品种为材料，计测叶片的裂叶数、叶长、叶宽、裂叶长、裂叶宽等叶片特征指标和叶片面积。分析叶片特征指标之间以及叶片特征指标和叶面积之间的关系，确定对叶面积影响较大的裂叶数（N）、最大裂叶长（L）、最大裂叶宽（W）和叶宽系数ρ（L/W）4个变量。通过模型拟合和优选，得到预测木薯叶面积的数学模型S=1.078L·W+3.931ρ-17.78。模型拟合结果，决定系数R2为0.966 3、均方根误差RMSE为9.846 9。模型外部验证结果，相关系数r为0.982 5、均方根误差RMSE为9.389 9。在模型中导入反映缺刻的特征变量，可以提高叶面积预测的准确度，增加了模型的适应性。该模型预测准确度高，观测方法简单，应用方便。

关键词 木薯；叶片特征指标；叶面积；模型

中图分类号 S533 文献标识码 A

Abstract In order to investigate the non-destructive determination of cassava leaf area quickly and accurately， nine cassava varieties including E25， SC5， SC6， SC7， SC8， SC9， SC101， SC124 and SC8013 were used to measure crack leaf number， leaf length， leaf width， crack leaf length， crack leaf width and leaf area. The characteristics of blades and the relationship between blade features and the leaf area were studied and crack leaf number（N）， the maximum crack length（L）， the maximum crack width（W）and the coefficient of crack width ρ（L/W）were determined to be the four variable indicators. Through the model fitting and optimization， a mathematical model to predict leaf area was built. Model fitting results revealed the coefficient of determination R2 was 0.966 3， RMSE was 9.846 9. The external validation of the model revealed the correlation coefficient r was 0.982 5， RMSE was 9.389 9. Introduced the feature variable of crack leaf in the model could improve the accuracy of prediction of the leaf area and increase the adaptability of the model. This model had a high prediction accuracy and was simple， which could be applied to scientific research and production.

Key words Cassava； Leaf feature index； Leaf area； Modeling

叶片是作物主要的光合器官[1]和重要的营养器官[2]。叶面积大小直接影响光能和水分利用效率以及干物质生产和作物产量[3]。长期以来，叶面积是生理生化、遗传育种、植物营养和作物栽培等研究的重要观测项目[4-9]。因此，快速准确地测定作物叶面积具有十分重要的意义。

作物叶面积测定方法可以分为破坏性测定法和非破坏性测定法。前者有方格法、称重纸法、求积仪法、鲜重法[10-13]等测定方法，这些方法只能进行破坏性的离体测量，不仅测定手续繁琐，而且需要一定的测定条件；后者包括便携式光电扫描仪法、系数法[10-13]等测定方法，这些方法可以进行非破坏性的活体测量，并且测定方法简单。然而便携式光电扫描仪法，由于扫描时拉动速度难以保持一致因而不可避免地产生测量误差。系数法目前主要应用于叶形规则和对称性好的叶片，如水稻、玉米、大豆、凤梨、三叶木通、雷公藤[14-16]；前人虽然对于有缺刻的非规则叶片进行研究，但多局限于叶面积与叶片长、宽的关系[17-19]，关于缺刻程度、缺刻数对叶面积影响的研究鲜见报道。

木薯个体较大，在研究和生产中很难满足破坏性测量所必需的样本数量[17]。然而关于木薯叶面积的非破坏性测定方法尚未见报道。为了实现木薯叶面积的非破坏性测定，本研究以9个木薯品种为材料，探讨通过叶片形态指标预测叶面积的可行性。

1 材料与方法

1.1 材料

试验材料来源于地处海南省儋州市宝岛新村的中国热带农业科学院热带作物品种资源研究所木薯种质资源圃，包括E25、华南5号（SC5）、华南6号（SC6）、华南7号（SC7）、华南8号（SC8）、华南9号（SC9）、华南101（SC101）、华南124（SC124）、华南8013（SC8013）9个木薯品种。2011年11月种植，种植密度为80 cm×100 cm，每亩施复合肥（N2 ∶ P2O2 ∶ K2O=17 ∶ 17 ∶ 17）15～20 kg，苗高50 cm后间苗，每株保留2个分枝。2013年6月采样，采样时叶片株高为150～290 cm不等，主茎完全展开叶片数在60片以上。

1.2 方法

1.2.1 样品采集 采样方法是从主茎或最大分枝的顶端开始由上至下每间隔1片叶采集1片叶片。每个样株采集约30片叶。样品采集后，为防止叶片失水蜷曲，立即用草纸压实固定形状。

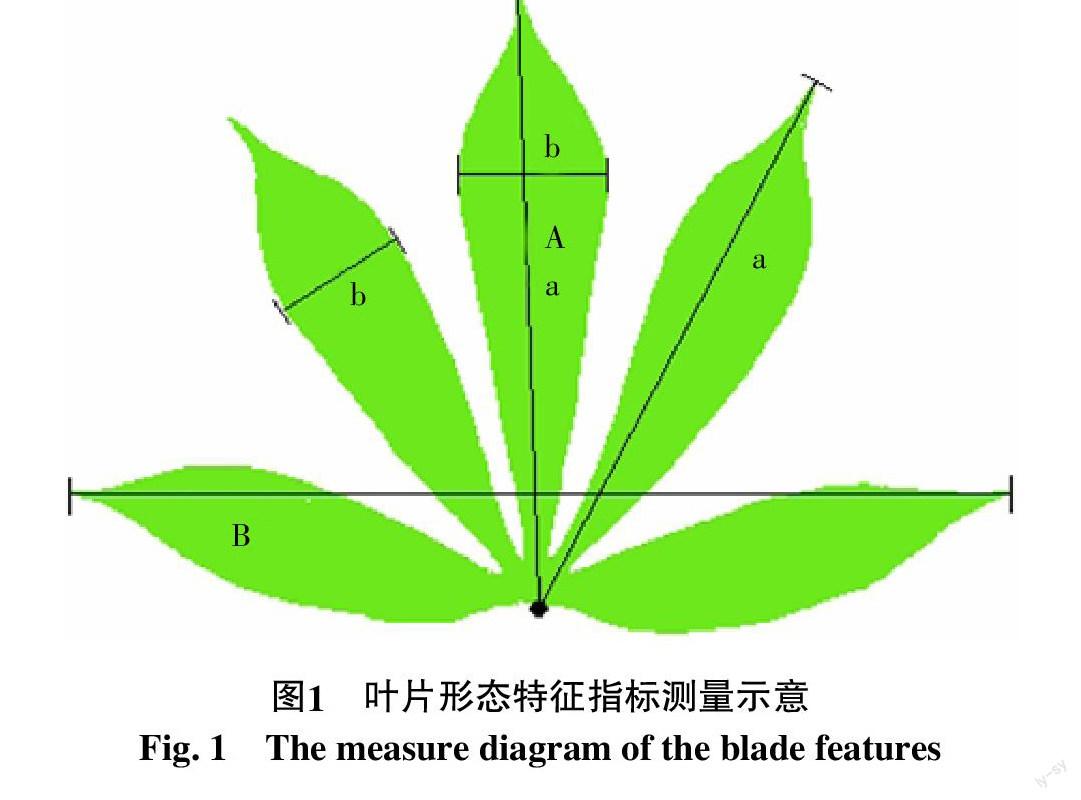
1.2.2 观测项目与测定方法 木薯叶片形态特征指标的观测方法如图1。叶长A为叶基部（叶柄与叶片连接处）至最长裂叶尖的距离，叶宽B为横向相距最远的两个裂叶叶尖的距离，裂叶长a为叶基部至裂叶尖的距离，裂叶宽b为裂叶最宽处的叶缘距离。

另外，计数每片叶裂叶数量，计算叶宽系数ρ即最大裂叶的长宽比（a/b）。

叶面积测定方法，采用扫描法测定每片叶的叶面积。先用HP Scanjet 2400扫描仪对叶片进行扫描，然后使用Lia 32软件分析计算扫描图像的面积。

1.3 数据处理

使用JMP 7软件进行数据分析和模型拟合。

2 结果与分析

2.1 木薯叶片的特征

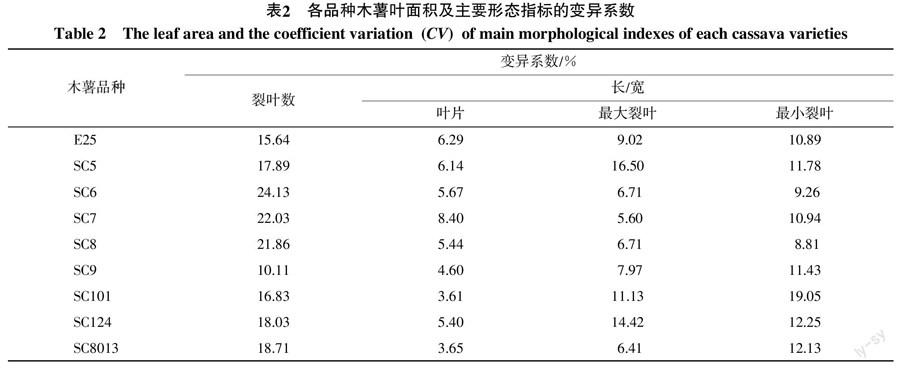
表1表明，木薯叶面积在11.1～297.6 cm2，变异系数（CV）为44.2%；裂叶数在3～9之间变化，变异系数为24.1%；叶宽在5.6～35.4 cm，变异系数为21.7%；叶长（最大裂叶长）在4.0～24.5 cm，变异系数为20.3%；最大和最小裂叶宽的变异系数在31%左右，最大和最小裂叶长的变异系数在21%左右，裂叶宽的变异系数大于裂叶长；叶宽系数在2.6～11.1，变异系数为46.5%；各形态指标的均值在品种之间存在显著差异。以上表明，各项形态指标的变幅较大，其中叶宽系数和叶面积的变异最大。

由表2可知，品种内叶片形态指标的变异性较小。在各项形态指标中，裂叶数的变异相对较大，叶片的长宽比和最大裂叶的长宽比的变异相对较小。

2.2 主要形态指标间的相关性分析

从表3可以看出，叶片形态指标与叶面积之间的相关系数在0.369 3～0.725 7，并且都达到5%显著水平。最大裂叶长（叶长）和叶宽之间高度相关；最大裂叶的长和宽与叶面积之间的相关系数大于最小裂叶的长和宽。

2.3 叶宽系数与叶面积的关系

最大裂叶宽与叶面积的关系如图2。虽然所有品种叶面积都随着裂叶宽的增加而增加，呈正相关关系，但是不同品种之间出现了明显的分层。当最大裂叶宽相同时，E25、SC124、SC5等品种的叶面积较大。

为了进一步探讨裂叶宽与叶面积的关系，对各品种的叶宽系数进行比较（表4）。结果表明，叶宽系数在品种间存在显著差异，E25最大、SC124其次。并且表4中叶宽系数的大小顺序与图2中各品种在最大裂叶宽在横轴上的排列顺序基本一致。表明叶宽系数和最大裂叶宽与木薯叶面积的大小之间存在内在联系。

2.4 预测木薯叶面积的数学模型与验证

按采样时间的先后次序进行间隔抽样，将观测获得的275组数据划分为3组，其中2组用于建模，1组用于模型的外部验证。基于多重共线性分析和上述各形态指标与叶面积之间的关系，确定以裂叶数N、最大裂叶长L、最大裂叶宽W及叶宽系数ρ为自变量构建预测木薯叶面积的数学模型。通过模型优选，得到预测木薯叶面积的模型（式①）。模型拟合效果，决定系数R2为0.966 3，均方根误差RMSE为9.846 9。

S=1.078L·W+3.931ρ-17.78 ①

基于模型预测的叶面积的外部验证结果如图3。木薯叶面积的预测值（x）与实测值（y）之间的回归方程如式②，相关系数r为0.982 5，均方根误差RMSE为9.389 9，表明模型预测的准确度很高。

y=1.020 5x-1.702 7 ②

为了评价裂叶数N和叶宽系数ρ对木薯叶面积预测模型的贡献度，在式1（模型1）的基础上衍生出另外3个模型。4个模型的外部验证结果如表5，通过比较模型的预测值与实测值的相关系数r和均方根误差RMSE的大小发现，模型4的预测效果最差，在模型4中导入N、ρ后r大幅度提高、RMSE大幅度降低。

3 讨论与结论

运用系数法测定非规则叶片叶面积，虽然前人以豚草、棉花、葡萄为材料进行了研究，但是在已有的经验公式或预测模型中，只有反映叶片大小的变量（如长、宽），没有反映叶片缺刻特征的变量[17-19]。关于木薯叶面积预测模型的研究尚未见报道。本研究基于叶片大小、缺刻特征等变量的预测木薯叶面积，取得了很高的预测准确度。在此主要就叶片缺刻特征变量对预测叶面积的贡献度以及本模型的适应性进行探讨。

木薯叶片具有缺刻深、裂叶数不等的特点，如果仅通过反映叶片大小的变量预测叶面积，难免会产生误差。本研究在预测模型中分别添加反映缺刻特征的叶宽系数和裂叶数后，预测叶面积与实测叶面积的相关系数r由原来的0.907 6、0.946 8、0.967 9提高到0.982 5，均方根误差RMSE由21.194 4、16.245 5、12.689 8下降到9.389 9，使预测准确度大幅度提高。本研究还发现，木薯叶面积的预测效果与叶片结构特征及其品种间的差异性有关。虽然木薯叶片的缺刻特征和形状在品种内变异较小，但是在不同品种之间变异较大，并且裂叶宽及叶宽系数对叶面积产生重要影响。因此，在模型中添加缺刻特征的裂叶数和叶宽系数2个变量后，减小和消除品种之间在缺刻上存在的系统差异，提高了预测的准确度。另一方面，由于裂叶数和叶宽系数2个变量可以消减因缺刻特征产生的误差，因此在增加了模型对不同类型叶片的适应性。可见，对于缺刻叶片特别是当缺刻的变异性较大时，在模型中导入缺刻特征的变量能够有效地提高模型的预测准确度。

综上所述，在木薯预测模型中导入反映叶片缺刻的特征变量，可以提高预测缺刻叶片叶面积的准确度，增加了预测模型的适应性。本研究基于叶片大小和缺刻特征构建的预测木薯叶面积的数学模型，不仅预测准确度高，适应性强，而且只需要观测最大裂叶的长、宽和裂叶数3个指标，方法简单，便于在科研和生产上应用。

参考文献

[1] 束怀瑞. 果树栽培生理学[M]. 北京： 农业出版社， 1993： 23-29.

[2] 吕忠恕. 果树生理[M]. 上海： 上海科学技术出版社， 1928： 21-86.

[3] 陈宗礼， 雷 婷， 齐向英， 等. 20个品种枣树叶面积回归方程的建立[J]. 生物学杂志， 2013， 30（1）： 86-90.

[4] 赵延明， 董树亭， 严 敏， 等. 玉米叶片叶绿素含量的发育遗传动态及环境互作效应分析[J]. 中国生态农业学报， 2008， 16（3）： 649-652.

[5] 刘晓宇， 陆 勇， 陈月琴， 等. 美洲黑杨苗期叶片主要营养物质含量及苗木生长性状的变异研究[J]. 江苏林业科技， 2011， 38（1）： 16-19.

[6] 李仙岳， 杨培岭， 任树梅， 等. 基于叶面积与冠层辐射的果树蒸腾预测模型[J]. 生态学报， 2009， 29（5）： 2 312-2 319.

[7] Li R T， Kojima N， Cui C H. Varietal difference in leaf nitrogen content and leaf area and their effects to ripening rate during mature period of japonica rice[J]. 东北农业大学学报（英文版）， 1999， 6（2）： 8l-88.

[8] Zhang R H， Kuusk A， Chen C， et al. A new quantitative way for determining leaf area index and net primary productivity in regional scale[J]. Journal of Geographical Sciences， 1996， 6（4）： 72-90.

[9] Dobermann A， Pampolino M F. Indirect leaf area index measurement as a tool for characterizing rice growth at the field scale[J]. Communications in Soil Science and Plant Analysis， 1995， 26（9-10）： 1 507-1 523.

[10] 王家保， 林秋金， 叶水德， 等. 5种测量热带果树单叶面积的方法研究[J]. 热带农业科学， 2003， 23（1）： 11-14， 23.

[11] 聂继云， 杨振锋， 张红军， 等. 果树叶面积简易测定方法研究[J]. 天津农学院学报， 2000， 7（4）： 33-35.

[12] 吴起明. 绿竹叶面积指数测定[J]. 福建林业科技， 2001， 28（2）： 68-70.

[13] 卢美英， 潘介春. 枇杷叶面积测定方法的研究[J]. 福建果树， 2003（1）： 1-3.

[14] 李永秀， 魏猷刚， 徐国彬， 等. 观赏凤梨叶面积指数的不同测定方法比较[J]. 江苏农业科学， 2008（4）： 159-161.

[15] 欧阳浩楠， 肖亚萍， 孙蓉蓉， 等. 三叶木通叶面积测量方法[J]. 安徽农学通报， 2008， 14（9）： 121-122.

[16] 涂育合. 雷公藤叶面积回归方程法测算[J]. 西南林学院学报， 2007， 27（4）： 16-19.

[17] 邓 旭， 王 娟， 谭济才. 豚草叶面积测定与回归分析[J]. 杂草科学， 2009（4）： 35-37.

[18] 吴 琳， 王修贵， 周复雄， 等. 一种棉花叶面积预测的简单方法[J]. 湖北农业科学， 2009， 48（6）： 1 326-1 329.

[19] 刘慧颖， 娄春荣， 董 环. 葡萄叶面积非离体测定新方法[J]. 北方果树， 2007（5）： 7-8.