基于径向函数（RBF）神经网络的建筑物沉降预测

张振林 白怀明 路新

【摘 要】RBF神经网络作为一种性能良好的前馈网络，具有更好的逼近能力和全局最优特性。本文采用了RBF 神经网络的建模方法来对建筑物的沉降进行预测。实践表明，该模型预测精度相对较高，有很好的实际应用价值。

【关键词】RBF神经网络； 建筑物沉降； 预测

Building settlement forecasting based on RBF neural network

Zhang Zhen-lin，Bai Huai-ming Lu Xin

（Survey and Design Institute ， Shandong Yellow River Jinan Shandong 250013）

【Abstract】As a kind of good performance of feedforward network， RBF neural network has a

better approximation ability and global optimal property. This practice shows that the model prediction accuracy is relatively high， and have a good practical application value.

【Key words】RBF neural network； Subsidence of building； Prediction

1. 径向基函数神经网络

1.1 径向基函数神经网络原理。

RBF神经网络一般是由输入层、隐层和输出层构成的三层前向神经网络，其拓扑结构可见下图1，输入层节点仅传递输入信号到隐层，隐层神经元一般采用高斯函数作为径向基函数，而输出层节点则通常是简单的线性函数。隐层节点的作用函数（基函数）将对输入信号在局部产生相应，也就是说，当输入信号靠近基函数中央范围时，隐层节点才会产生较大的输出信号，由此可以看出该网络具有局部逼近能力，因此径向基函数网络又称为局部感知场网络[3]。

1.2 RBF网络建模。

RBF网络用于非线性系统辨识和系统建模一般分为以下几个步骤。

（1）选择恰当的学习样本。在许多文献中，系统辨识的学习数据都是用伪随机码激励系统得到，但在过程控制中，这是不适用的。无论采用什么方法得到的学习数据都必须遵循一条原则，即学习样本必须充分体现系统的工作状况。

（2）学习样本数据的预处理。通常学习数据都应做归一化处理，同时由于在实时控制中采集到的数据含有噪声，因此有必要做有滤波的处理过程。

（3）确定模型的阶次。可以应用被建模系统的先验知识来确定，同时也可通过数据分析得到。

（4）采用恰当的学习算法完成RBF网络的离线学习。

（5）倘若系统是时变的，必须用递推算法对RBF网络进行在线校正。

2. 工程应用

2.1 工程概况。

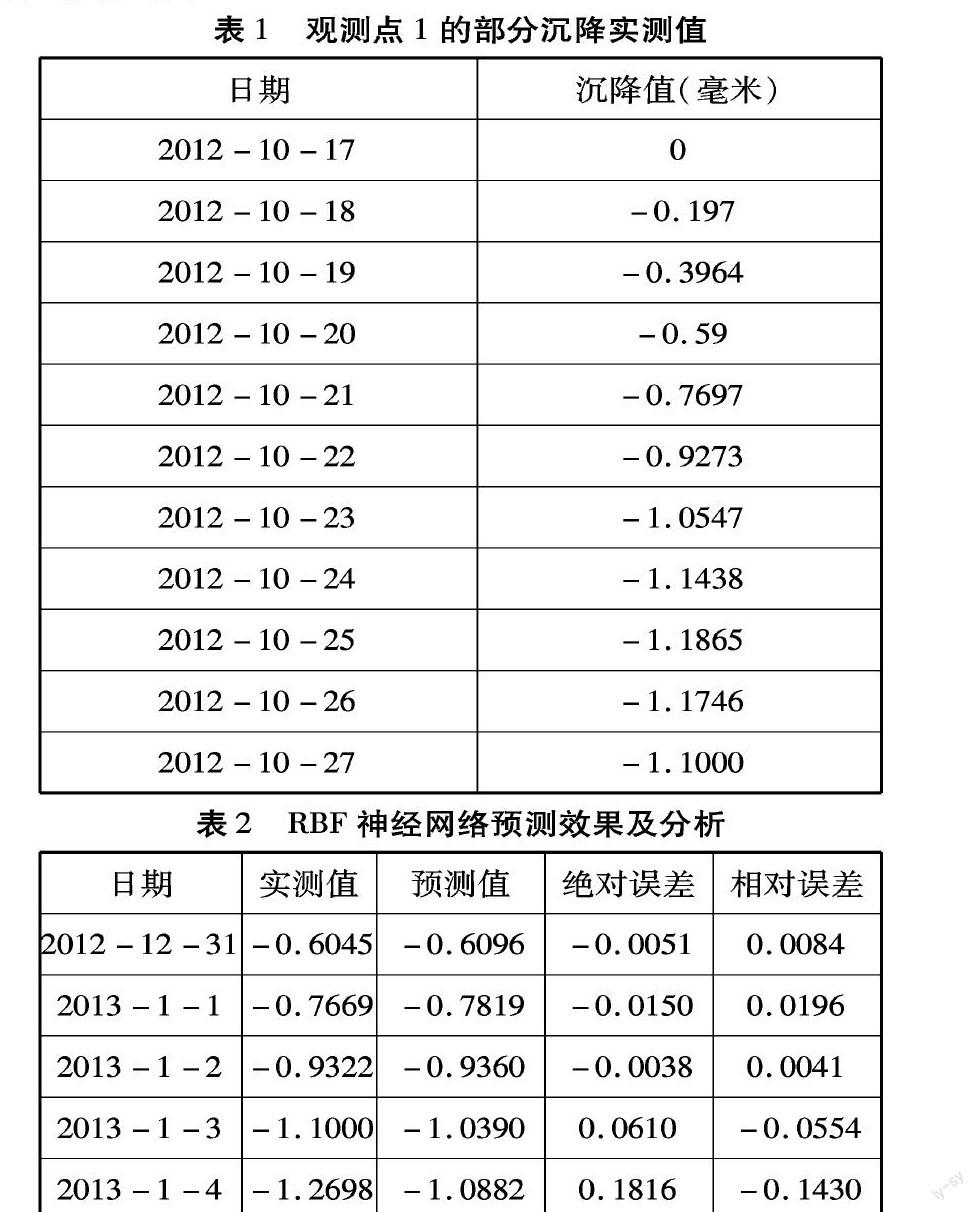
本工程工地位于山东省济南市，此处正在修建一个大型的农贸市场，正处于开挖基坑阶段。该开挖基坑东西方向长约55m， 南北方向长约60m，开挖深度12.5m ，安全等级为一级；基坑周围均为六层高的居民楼，且一楼均为一些商铺，环境相对偏僻。为了了解由于基坑的开挖对周围居民楼的影响状况，因而特别布设一些监测点来进行沉降观测。本文所用数据主要是监测点1的实测值。

2.2 实测数据的预处理。

本监测从2012 年10月17日开始监测工作， 至2013年1月4日结束。1点的监测样本数目为N=80，利用前75个沉降值建立径向基神经网络模型，后5个沉降值作为预测的实测参考值。沉降观测点安装在基坑周边建筑物的支柱上， 在基坑开挖过程中定期观测其沉降值。通过对测点1各个时期的高程值进行一阶差分，得到沉降值。有以下数据可以看出，经过差分之后的数据序列成为相对平稳的序列，如表1所示。

2.3 RBF神经网络模型的预测。

（1）为了更好地验证该预测模型在工程中的应用效果，分别设计了2种方案来对沉降观测数据进行建模分析。方案一：RBF神经网络模型。方案二：传统的回归模型；最后给出各种方案的实验结果。

（2）方案一：RBF神经网络模型。对选定的样本序列，根据建模阶段设定的误差目标误差和均方误差最小的原则，利用MATLAB神经网络工具箱提供的Newrb函数设计一个径向基网络，它可以根据设定的最大隐藏神经元的个数，自动增加径向基网络的隐层神经元的个数，直到均方误差满足为止。【4】然后再将满足要求的的径向基网络应用于后期阶段的仿真，进而计算出预测残差值。最后用建模阶段和预测阶段均方误差来衡定其预测效果。预测效果（如下图1中Figure3，4所示）及分析如表2所示。

（3）方案二：传统的回归模型。对选定的样本序列，根据均方误差最小的原则，利用MATLAB编程从阶数p=1开始到p=75自动搜索来确定回归模型的阶数，然后按照最小二乘参数法估计出各阶参数，同时计算出相应的系数值， 然后计算出预测残差值，最后用建模阶段和预测阶段均方误差 （其中 为预测残差，k为预测期数）来衡定其预测效果。预测效果（如下图1中Figure5，6所示）及分析如表3，4所示。

（4）由以上结果分析得知：相对于传统的回归模型来讲，RBF神经网络模型不管是在建模阶段，还是在预测阶段精度都相对较高。这进一步验证了RBF 神经网络作为一种性能良好的前馈网络，具有更好的逼近能力和全局最优特性。

3. 结语

本文是径向基函数（RBF）神经网络在建筑物沉降预报中的初步应用，工程应用实例则是以建筑物沉降时间序列为基础，采用 RBF 神经网络建立建筑物沉降预测模型，通过最近邻聚类学习算法实现建筑物沉降预测，具有结构简单、学习速度快、预测精度高的特点，网络的外推能力也较强。实际应用结果表明，该方法具有十分理想的预测效果，在建筑物沉降预报中具有广泛的应用前景。

参考文献

[1] 王炜，吴耿锋，张博锋等 径向基函数（RBF）神经网络及其应用 [J]地震，2005.4：20～22.

[2] Moody J，Darken C. Learning with localized received fields[A]. In：Hinton TG，Sejnowski Ted. Proceedings of the 1988 Connectionist Models SummerSchool[C]. Menlo Park，CA：Morgan Kaufmann.

[3] 农吉夫，金龙 基于 MATLAB 的主成分RBF神经网络降水预报模型 [D]热带气象学报，2008.12：714～716.

[4] 闻新，周露，王丹力等 MATLAB神经网络应用设计 [M]北京：科学出版社，2000.

[5] 国家一、二等水准测量规范 GT/T12897-2006 .

[6] 建筑变形测量规范 JGJ8-2007.