基于解微分方程的地铁牵引供电系统故障测距

王雅茹，冯海锋，谢瑞，黄彦全

(西南交通大学电气工程学院，四川 成都 610031)

1 引言

地铁牵引供电系统直流侧发生短路故障时，为缩短故障停电时间，在短时间内找出故障点，尽快将故障排除，需快速且准确地定位故障点，因此研究地铁牵引供电系统故障测距方法，对地铁供电系统安全运营有重要意义［1］。

国内对地铁供电系统直流侧故障测距方法研究较少，可借鉴电力系统常用的故障测距方法。故障测距方法按照测距原理主要分为故障分析法和行波法，按照所使用单双侧数据又分为单端法和双端法［2］。电力系统中行波法应用广泛，行波在波阻抗不连续处会发生反射和折射，从而给单端行波测距方法后续行波的识别带来难点［3］;另外地铁牵引供电系统中，接触网结构复杂，线岔、锚段关节、分段绝缘器等波阻抗不连续处很多，不利于单端行波测距方法在地铁牵引供电系统中的应用［4］。单端故障分析法主要包括解微分方程和工频阻抗法、迭代法、解一元一次方程法和电压法。针对三相电力系统发展出来的阻抗法大多数使用工频分量进行故障测距，无法应用于地铁牵引供电系统的故障测距中［5，6］;阻抗法中不使用工频分量的特例是解微分方程法和电压法，而电压法的理论基础是行波传输理论，地铁牵引供电系统由于牵引变电所间距太短，电压等级低，行波过程不明显，因而该方法也不适用于地铁牵引供电系统直流侧的故障测距中。双端测距法采用双端数据测距，对录波装置要求很高，且时间是否同步对测距结果影响很大［7］。

上述方法直接应用到地铁故障测距中均有所不足。解微分方程法是通过对输电线路模型建立微分方程，求解故障点距离，理论上可行，此法最重要的问题是消除过渡电阻的影响，本文针对地铁牵引供电系统提出了一种基于解微分方程的双端不同步测距法。

2 理论分析

地铁牵引供电系统主要包括牵引变电所和牵引网。牵引变电所主要功能是通过变压器和整流器将中压电网中的三相交流电转换成低压直流电。牵引网通常采用双边供电方式［8］。

建立地铁牵引供电系统仿真模型，需考虑对整流所和牵引网的处理，一般在直流稳态中是不考虑电感的存在，而在短路瞬间的暂态过程中可将牵引网中接触网和走行轨等效为电阻串联电感，在此可假设接触网和行走轨单位长度的电感和电阻值为定值。同时整流变电所可等效为直流电压源和电阻串联［9］。建立牵引网双边供电模型，当接触网发生短路时的暂态模型如图1所示。

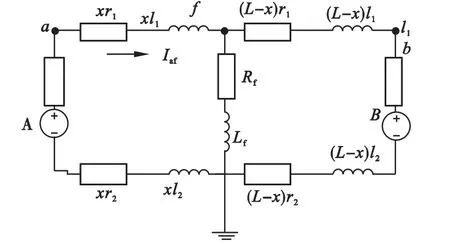
图1 牵引供电系统短路暂态模型

牵引网发生故障时，受到电感影响，短路电流波形在短路后的暂态过程中是类似于指数形式的。短路点过渡电阻电感分别用Rf、Lf表示，接触网单位电阻r1，单位内电感l1;行走轨单位电阻r2，单位内电感l2。假设模型中接触网f点对行走轨发生短路，此时对暂态过程有微分方程:

又可假定

于是

简化为

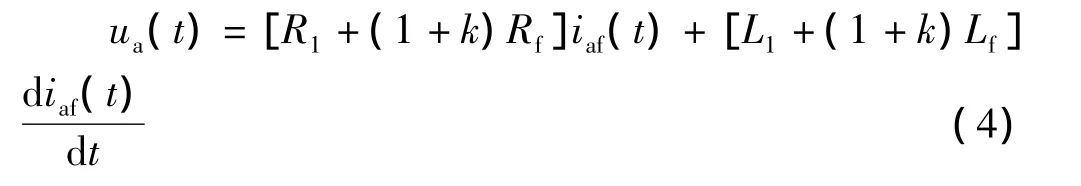
其中

R1=x(r1+r2)

L1=x(l1+l2)

令

R左=R1+(1+k)Rf

L左=L1+(1+k)Lf

则(4)式变为:

如果进行n次观测，则各误差的平方和为:

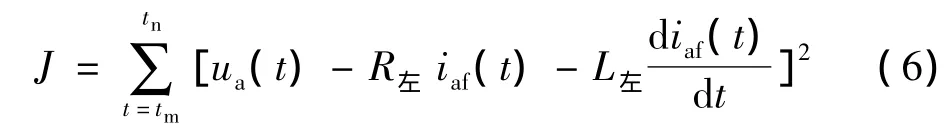
要使J达到极小值，分别对R左和L左求偏导，得到:

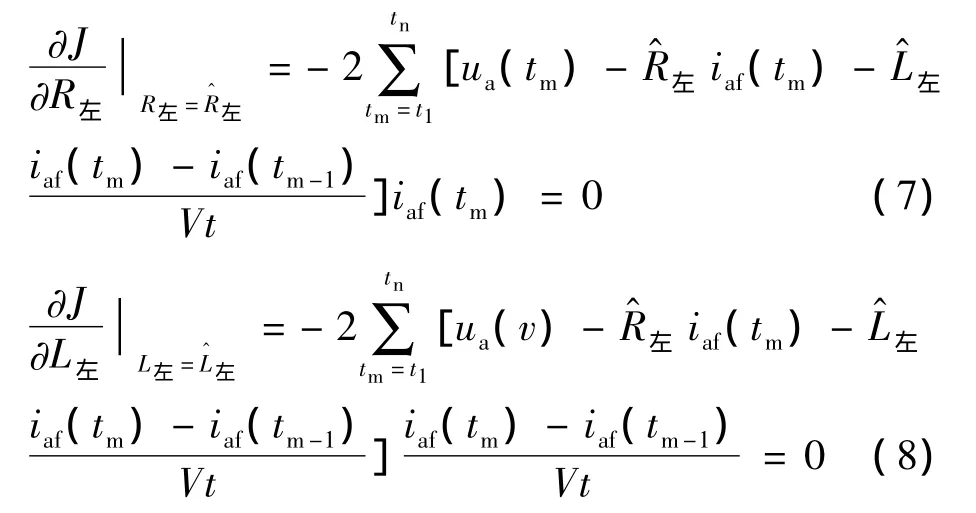
解由式(7)和式(8)组成的二元一次方程组，可以得出电感参数左和电阻参数左估计值的计算公式分别为:

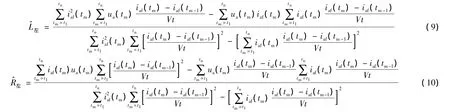
在a、b两个数据采集点所读取的电压电流数据中分别取n个采样点，根据(9)、(10)式采用最小二乘法分别求出左右侧的电阻值和电感值。

左右牵引网电阻电感参数又有如下关系:

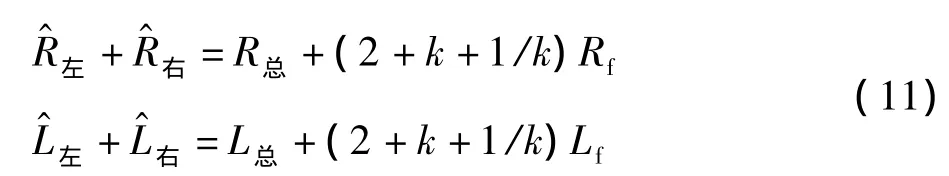
上式中 k、Rf、Lf为未知量。

可通过下式求得k值:

其中，Rb为右侧电源内阻;Ub为右侧电源额定电压。

取2n采样点得到方程组后对其求解，即可求出k值的准确值。

又

求得k、Rf代入下式即可求得故障点距离:

3 PSCAD仿真实例

线路全长4km，过渡电阻Rf=1Ω，Lf=0.1mH，短路故障在0.1s时刻发生。牵引供电系统采用双边供电，电源电压输出恒定为1650kV，各参数数值为:

r1=0.028Ω/km，l1=2.663mH/km，r2=0.023Ω/km，l2=1.78mH/km［8］。

依据理论及实际数据建立如图2的模型。

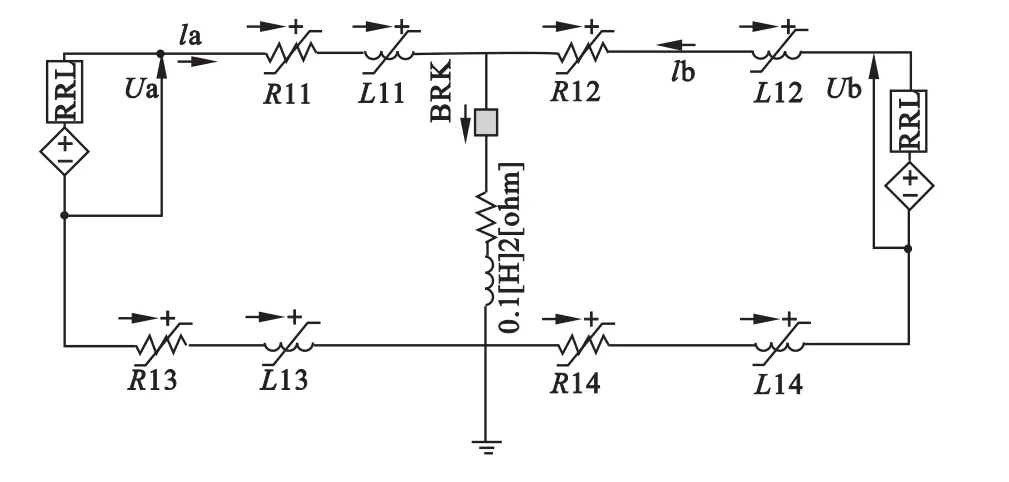
图2 仿真模型图

短路点f距离牵引变电所a为100m时，从牵引变电所a、b端测得的短路电压电流波形如图3所示。

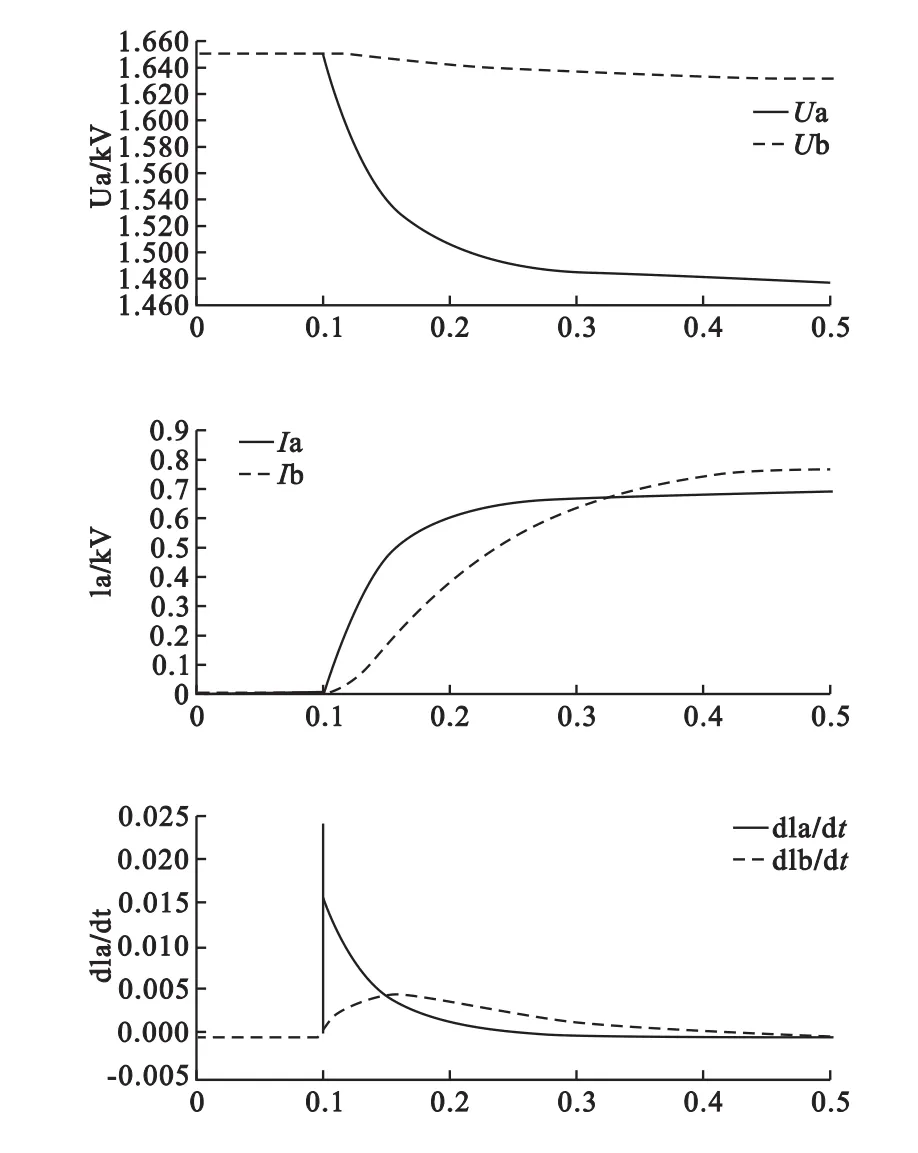
图3 ua和 ub、ia和 ib、dia/dt和 dib/dt仿真波形图

利用最小二乘法求解微分方程，左右牵引网电阻电感参数估计值结果如表1所示。

表1 Rf=1Ω时左侧牵引网电阻电感参数估计值与实际值对比表

计算得到k值如表2所示。

表2 Rf=1Ω时k的计算值

设置短路点f距牵引变电所距离分别是100m，500m，1500m，2000m。使用电阻估计值计算所得测距结果如表3所示。

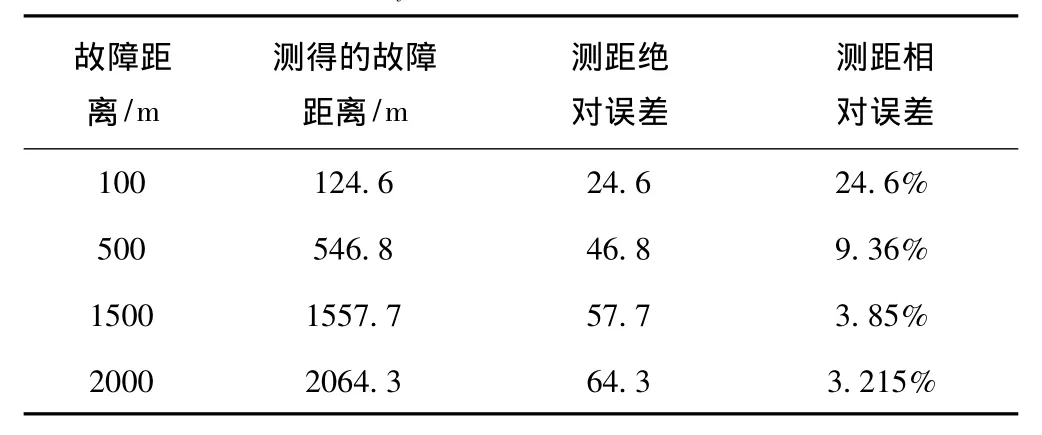
表3 Rf=1Ω时使用测距结果

线路其他参数不变，过渡电阻Rf=2Ω时故障设在100m处的仿真波形如图5所示。

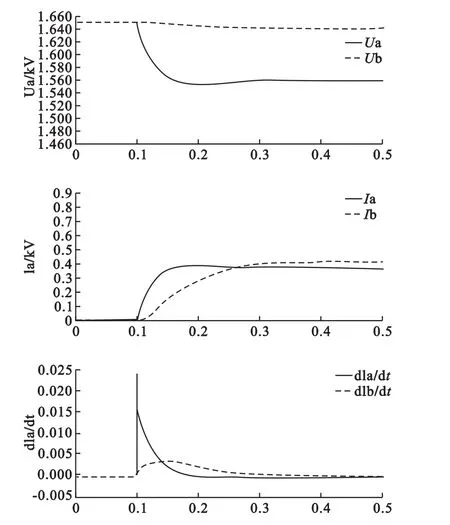
图4 Rf=2Ω、100m 处故障点时 ua和 ub、ia和 ib、dis/dt和dib/dt仿真波形图

根据仿真数据计算结果如表4所示。

表4 Rf=2Ω时右侧牵引网电阻电感参数估计值

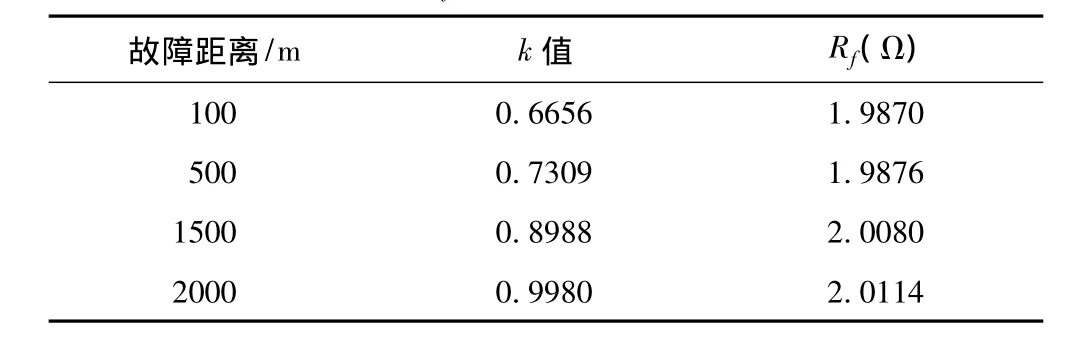
表5 Rf=2Ω时k的计算值

此时，使用电阻估计值计算所得测距结果如表6所示。

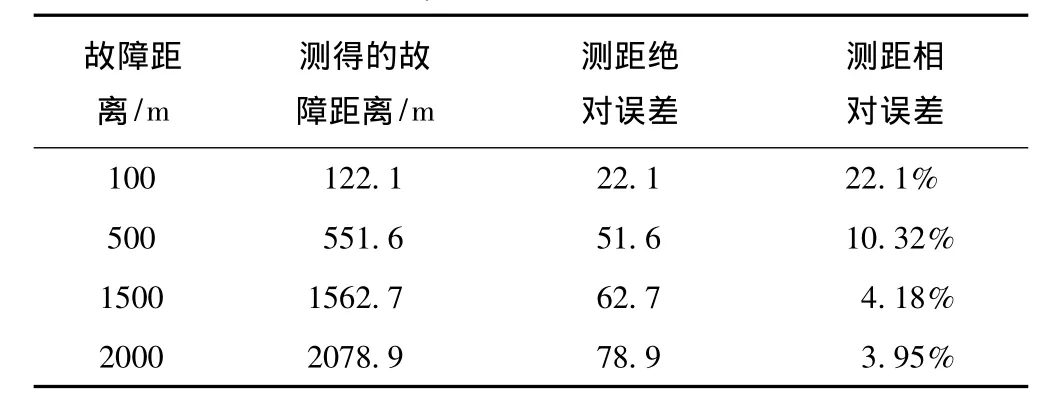
表6 Rf=2Ω时的测距结果

从表3和表6测距计算结果说明，改变过渡电阻的值对测距计算结果影响不大，近端短路测距相对误差为20%，虽然相对误差较大，但绝对误差值依然是可以接受的;在线路中段时测距误差在5%以内，说明此测距方法具有有效性。算法的误差主要是由差分代替微分引起的，同时值计算也存在一定误差，可通过提高采样频率即增加测距所用的采样点数，可有效减小测距误差。

4 结论

本文将解微分方程法应用到地铁牵引网故障测距，利用双端不同步的数据，即左右侧数据是分别进行计算，应用简单方便。利用PSCAD软件仿真，计算结果表明此算法能够减小过渡电阻的影响，测距误差在可接受范围内，测距结果较为准确。

［1］何宗华，汪松滋，何其光.城市轨道交通供电系统运行与维修［M］.北京:中国建筑工业出版社，2005.

［2］葛耀中.新型继电保护与故障测距原理与技术［M］.西安:西安交通大学出版社，2007.

［3］张煜.高压架空输电线路单端故障测距装置的研究［D］.北京:华北电力大学(北京)，2004.

［4］周文卫.直流牵引供电系统短路电流计算与故障测距研究［D］.硕士毕业论文，2011，(1):50.

［5］周文卫，陈丹，陈立扬，等.一种改进的地铁故障测距方法及应用［J］.城市轨道交通，2012.

［6］索南加乐，齐军，陈福锋，等.基于R－L模型参数辨识的输电线路准确故障测距算法［J］.中国电机工程学报，2004，24(12):119－125.

［7］黄德胜.地下铁道供电［M］.北京:中国电力出版社，2010.

［8］赵顺.地铁接触网故障测距研究及实现［D］.2011，(1):3－5.

［9］张健，肖书印，张友鹏.地铁供电系统短路试验的仿真分析［J］.都市快轨交通，2008，(8).