不含某些图作为导出子图的图的色数

段 芳

（新疆师范大学数学科学学院，新疆乌鲁木齐830054）

不含某些图作为导出子图的图的色数

段 芳

（新疆师范大学数学科学学院，新疆乌鲁木齐830054）

Erodo¨s证明了对于任意一个图G，χ（G）－ω（G）可以任意大。因此，对一般图而言，其色数不一定能找到一个与团数有关的上界。文章主要讨论一类特殊的F－free图的色数和团数的关系。设图G＝（V，E）是一个不含K1，k+1+e、C4和C4+e为导出子图的连通图，不是星图和奇圈。若α（G）≥k≥3，则χ（G）≤（k（k－1）／2）ω（G）。

色数；团数；F－free图

文章只考虑不含环和重边的有限无向图。给定一个图G＝（V（G），E（G）），用｜V（G）｜表示图G中点的个数，称为图G的阶数，用n来表示。取S是V（G）的一个非空子集，称点集为S，S中的点相邻当且仅当它们在图G中相邻的图为S在图G中的导出子图，记为G［S］。若G［S］中没有边，则称S是独立集；若G［S］是完全图，则称S是团。图G最大独立集中点的个数称为独立数，用α（G）表示；图G的最大的团中所含点的个数称为团数，用ω（G）表示。如果图G的点集可以划分成k个独立集，则称k的最小取值为图G的色数，记为χ（G）。另外，用G－S表示在图G中去掉点集S中的所有点以及与点集S中的点所关联的所有边得到的图。

早在七十年代，Chartrand等人在文献［1］中就提出了不含某些图作为导出子图的图的概念：对于给定的一些图构成的集合F，若图G不包含与集合F中任一图同构的导出子图，称图G是不含某些图作为导出子图的图。特别的，当k＝1且H1＝K1，3时，图G称为无爪图。这类图倍受大家关注，有很多这方面的结论。如：文献［3］和［5］中分别得到了不含K1，4和K1，4+e作为导出子图的图的一些结果。文献［6］中得到clawfree图的一些结果。

图的色数、团数和独立数有密切的关系，对任意图G，很容易看出χ（G）≥ω（G）且χ（G）≥但对一般图而言，其色数不一定能找到一个与团数相关的上界。对于很多不含四个点的图作为导出子图的图类，已有色数与团数有关的一些结果：Chudnovsky和Seymour在文献［2］中证明了如果G是一个α（G）≥3的无爪图，则χ（G）≤2ω（G）。文献［7］中证明了对不含K1+P3和C5作为导出子图的图G，有χ（G）≤ω；文献［4］中证明了如果G是一个不含2K1+K2和C5作为导出子图的图，若ω（G）＝2，则χ（G）＝ω（G）；若ω（G）≥3，那么χ（G）≤2ω（G）32。文章将在特殊的图类上讨论这个问题。

令图C4+e表示将圈C4中的两个度为2的点连接而得到的图。文章证明了当α（G）≥k≥3时，若图G是一个连通的不含K1，k+1+e、C4和C4+e作为导出子图的图，那么χ（G）≤（k（k－1）／2）ω（G）。

1 主要结论

在下面的证明中，用符号NG（v）表示点v∈V（G）在图G中所有邻点构成的集合。

定理 图G＝（V（G），E（G））是一个不含K1，k+1+e、C4和C4+e作为导出子图的连通图，不是星图，也不是奇圈。若α（G）≥k≥3，则χ（G）≤（k（k－1）／2）ω（G）。

证明 图G不是奇圈，又因为α（G）≥k≥3，所以图G不是完全图。因此由Brook定理可以得到χ（G）≤Δ（G）。如果要证明χ（G）≤（k（k－1）／2）ω（G），只需要证明Δ（G）≤（k（k－1）／2）ω（G）即可。

下面通过对图G的点数｜V（G）｜进行归纳来证明这个结论。取点v是图G中一个度为Δ（G）的点。因为α（G）≥k，如果V（G）＼｛v｝中所有的点都和点v相邻，那么点v至少有k个互不相邻的邻点，不妨设这些邻点所构成的点集为A＝｛a1，a2，…，ak｝。又因为图G不是星图，因此至少存在一个不属于集合A的点u，使得点u至少和集合A中某一个点相连。下证点u只能和集合A中一个点相连。否则，若点u和A中两个点ai和aj都相邻，那么图G［u，v，ai，aj］导出了图C4+e，与已知条件矛盾。但若u只和A中一个点ai连接，那么图G［u，v，a1，…，ak］又导出了子图K1，k+1+e，与已知条件矛盾。因此在V（G）＼｛v｝中不是所有的点都和点v相邻，可设存在一个点w∈V（G），w≠v且w和v不相邻。这时总可以选择点w使得G－｛w｝是连通的（只需要选择一个距离点v最大的点即可）。且显然有α（G－｛w｝）≥k－1。

如果α（G－｛w｝）≥k，那么根据归纳假设得到Δ（G－｛w｝）≤（k（k－1）／2）ω（G－｛w｝）。显然有ω（G－｛w｝）≤ω（G），又因为w和v不相邻，所以Δ（G）＝Δ（G－｛w｝）。这时Δ（G）＝Δ（G－｛w｝）≤（k（k－1）／2）ω（G－｛w｝）≤（k（k－1）／2）ω（G），得证。

因此下面可以假设α（G－｛w｝）＝k－1。令集合A＝｛a1，a2，…，ak－1｝⊆V（G－｛w｝）是图G－｛w｝的独立集。取集合Ni＝NG－｛w｝（ai），集合Mi＝Ni＼（∪j≠i，1≤j≤k－1Nj），这里i＝1，2，…，k－1。且令集合Mij＝Ni∩Nj，这里1≤i，j≤k－1，i≠j。因为已知α（G－｛w｝）＝k－1，所以图G－｛w｝中每一个点要么在独立集A中，要么在某一个点集Ni中。下面可证G［Mi∪｛ai｝］是一个团。用反证法，如果在Mi中存在两个点x，y不相邻，那么点集｛x，y｝∪A＼ai就是G－｛w｝中一个点数为k的独立集，与条件α（G－｛w｝）＝k－1矛盾。因此G［Mi∪｛ai｝］是一个团。

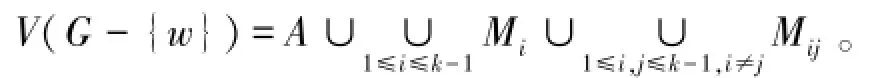
特别的，如果取k＝2，可以得到如下推论。

推论 图G＝（V，E）是一个不含K1，3+e、C4和C4+e作为导出子图的连通图，不是星图，也不是奇圈。若α（G）≥k≥3，则χ（G）≤ω（G）。

参考文献：

［1］G.Chartrand，D.Geller and S.Hedetniemi，Graphs with Forbidden Subgraphs［M］.J.Combin.Theory，1971，（10）：12－41.

［2］Maria Chudnovsky and Paul Seymour.Claw－free graphs VII.Colouring clawfree graphs［M］.Manuscript，2004.

［3］F.Duan，G.Wang，Note on the longest paths in｛K1，4，K1，4+e｝－free graphs［J］.Acta Math.Sinica，2012，28：2501－2506.

［4］F.Duan，Baoyin.Wu.On chromatic number of graphs without certain induced subgraphs［M］.Ars combinatoria，2011，6：33－44.

［5］R.Li，Hamiltonicity of 2－connected｛K1，4，K1，4+e｝－free graphs［J］.Discrete Math，2004，287：69－76.

［6］T.Runli and X.Liming，On hamiltonicity of 2－connected claw－free graphs［J］.Appl.Math.J.Chinese Univ，2012，（27）：234－242.

On Chromatic Number of Graphs without Certain Induced Subgraphs

DUAN Fang
（School of Mathematical Sciences，Xinjiang Normal University，Urumqi，Xinjiang，830054，China）

In general，there is no upper bound on the chromatic number of a graph in terms of its clique num⁃ber，since by a classical result of Erodo¨swe know that the differenceχ（G）－ω（G）can be arbitrarily large.In this thesis，we shall focus on F－free graphs and obtain results that the chromatic number of F－free graphs has upper bound in terms of their clique number。LetG be a｛K1，k+1+e，C4，C4+e｝－free graph，if α（G）≥k≥3，then χ（G）≤（k（k－1）／2）ω（G）.

Clique number；Chromatic number；F－free graph

O157.5

A

1008⁃9659（2015）01⁃0022⁃03

2014－11－30

段 芳（1979－），女，辽宁大连人，硕士，主要从事图论方向的教学与研究。