基于二进提升格式构造具有高阶消失矩的二进小波滤波器

汪艳丽， 吐尔洪江·阿布都克力木， 陆艳飞

（新疆师范大学数学科学学院，新疆乌鲁木齐830054）

基于二进提升格式构造具有高阶消失矩的二进小波滤波器

汪艳丽， 吐尔洪江·阿布都克力木， 陆艳飞

（新疆师范大学数学科学学院，新疆乌鲁木齐830054）

文章利用提升格式和对偶二进提升格式，分别构造出新的具有8阶高消失矩的提升二进小波滤波器和具有6阶高消失矩的对偶提升二进小波滤波器。第一步：对Mallat所构造的B－样条二进小波（r＝1）进行拓展，通过大量的计算，反复实验，最后进行证明，可以得到构造新的B－样条二进小波的方法；第二步：运用上述构造二进小波的新方法，构造出新的B－样条二进小波（r＝2）作为初始二进小波滤波器，再基于二进提升格式和对偶二进提升格式，分别进行三次提升，推导出具有有限长、线性相位、高阶消失矩的提升二进小波滤波器和对偶提升二进小波滤波器，而这些提升的二进小波滤波器并不能通过Sweldens提升格式进行计算获得，只能有本文所述的二进提升格式得到。

高阶消失矩；二进提升格式；二进小波滤波器

小波理论［1］是当前数学研究领域中一个迅速发展的新领域，是在Fourier级数的基础上发展起来的，是继Fourier变换之后又一新型有效的信号处理工具［2］。由于其同时具有提供时间和频率分析的能力，因而能有效的从信号中提取信息，通过对尺度因子进行平移和伸缩等运算，对信号或函数进行多尺度的细化分析（Multiscale Analysis），解决了很多Fourier变换不能解决的困难问题［3］。因而小波在信号处理方面备受关注，小波变换在信号处理领域被认为是“最完美的分析手段”［4］。目前，国内外已经有很多关于设计小波滤波器方法的研究［5，6］，小波的应用和理论研究紧密地结合在一起，在信息科技等很多领域都取得了令人瞩目的成就［7］。近年来，随着小波分析的应用领域越来越广阔，数学研究的专家和学者们在小波滤波器的设计方法上取得了非常不错的成果［8，9］。其中，Sweldens提升格式［10，11］就是设计小波滤波器方法中的一种，然而，构造二进小波滤波器却并不能运用Sweldens提升格式，因为这种提升格式只能构造双正交小波滤波器，对于二进小波滤波器的构造，这种提升格式也无能为力。因此，本文给出了构造B－样条二进小波的新方法以及二进提升格式。从新构造的（r＝2，m＝1）B－样条二进小波滤波器出发，分别运用二进提升格式和对偶二进提升格式，构造出新的具有8阶高消失矩的提升二进小波滤波器和新的具有6阶高消失矩的对偶提升二进小波滤波器。本文从五方面对构造新的二进小波滤波器方法进行论述：第二部分先给出了构造新的B－样条二进小波的方法；第三部分介绍了二进提升格式及对偶二进提升格式；第四部分分别运用二进提升格式和对偶二进提升格式，构造出新的具有高阶消失矩的提升二进小波滤波器和对偶提升二进小波滤波器；最后，在第五部分进行了总结。本文中推导出的新的提升二进小波滤波器和对偶提升二进小波滤波器均具有较高的消失矩，而在具体实验中，小波消失矩的阶数越高，其光滑性就越好，在频域内的衰减性就越快，且其频谱定域性就越好。

1 B－样条二进小波构造的新方法

对B－样条二进小波（Mallat构造r＝1）进行拓展，得到构造新B－样条二进小波的一种方法。

m次B－样条是I［0，1］与其自身的m+1卷积的平移，其Fourier变换有

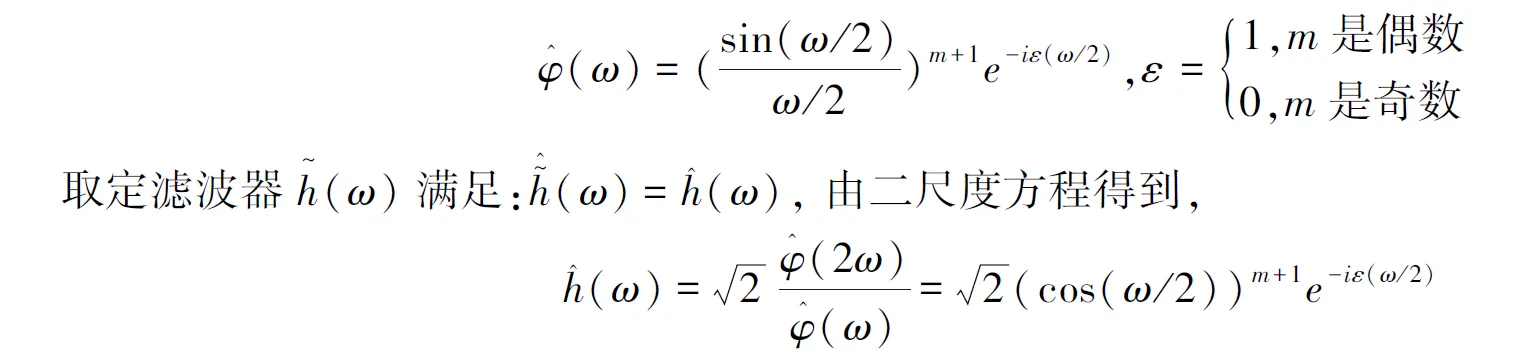
那么，由二进完全重构条件可以推出，

最后，由二尺度方程可以得到新的二进小波

2 二进提升格式及对偶二进提升格式

定义1（二进提升格式） 设初始二进小波滤波器为｛hk，gk，｝，那么提升滤波器的系数由

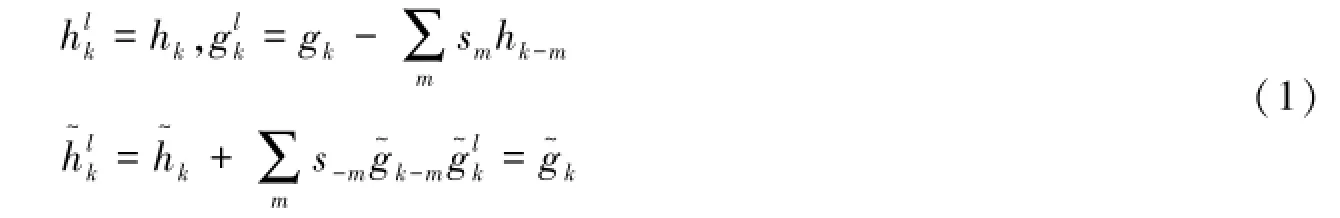
确定，称为二进提升格式，sm为提升参数。

定义2（对偶二进提升格式） 设初始二进小波滤波器｛hk，gk｝，那么滤波器的系数由

确定，称为对偶二进提升格式，rm为提升参数。

定理1 （1）若定义1中的初始分解二进小波高通滤波器g的Fourier变换满足（0）≠0，那么′（0）＝0的充分条件是0）＝（0）（0）。

（2）若初始分解二进小波高通滤波器g具有p阶消失矩，那么运用定义1提升后的二进小波分解高通滤波器（ω）具有至少p+1阶消失矩的充分条件是（ω）满足：

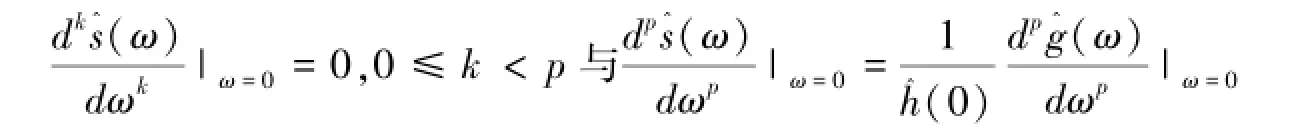
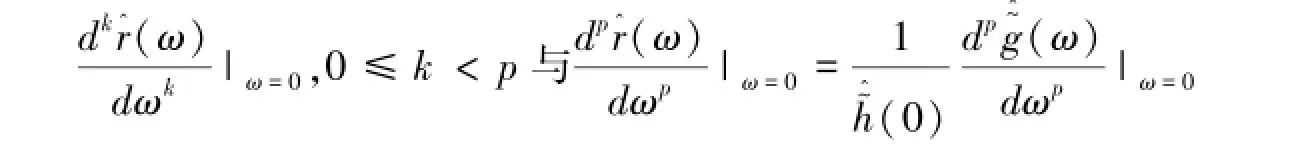
3 新的具有高阶消失矩的二进小波滤波器的构造

设定r＝2，m＝1构造二进小波，得到新的二进小波滤波器。从新构造的（r＝2，m＝1）B－样条二进小波滤波器出发，分别运用二进提升格式和对偶二进提升格式，构造出新的具有8阶高消失矩的提升二进小波滤波器和新的具有6阶高消失矩的对偶提升二进小波滤波器。

3.1 利用定义1构造具有8阶消失矩的提升二进小波滤波器

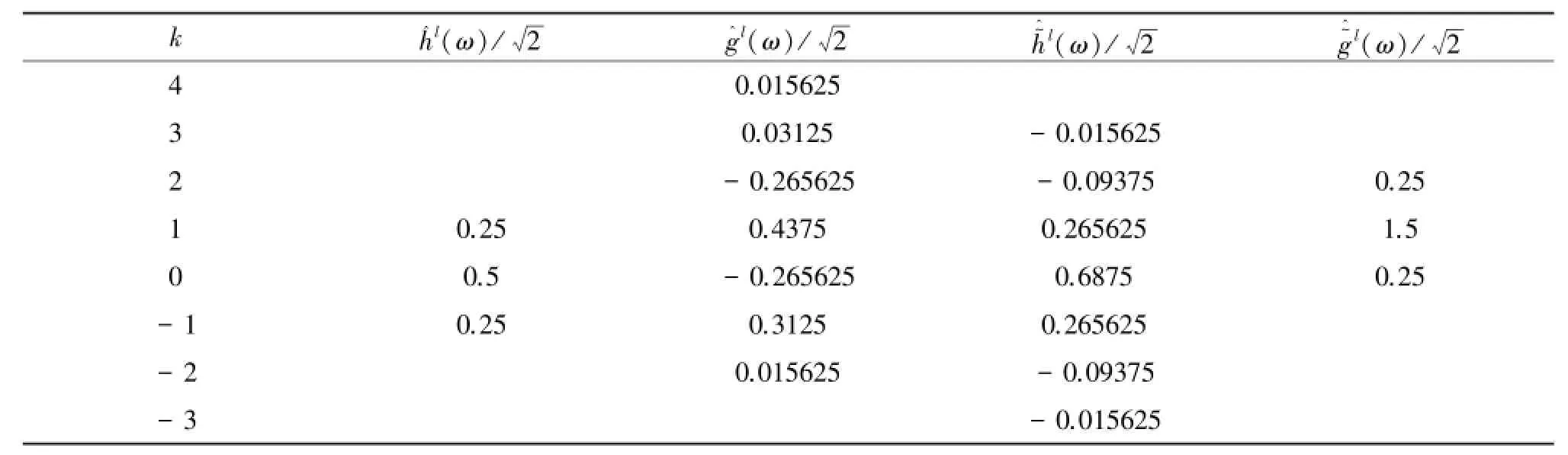
表1 第一次提升二进小波滤波器系数

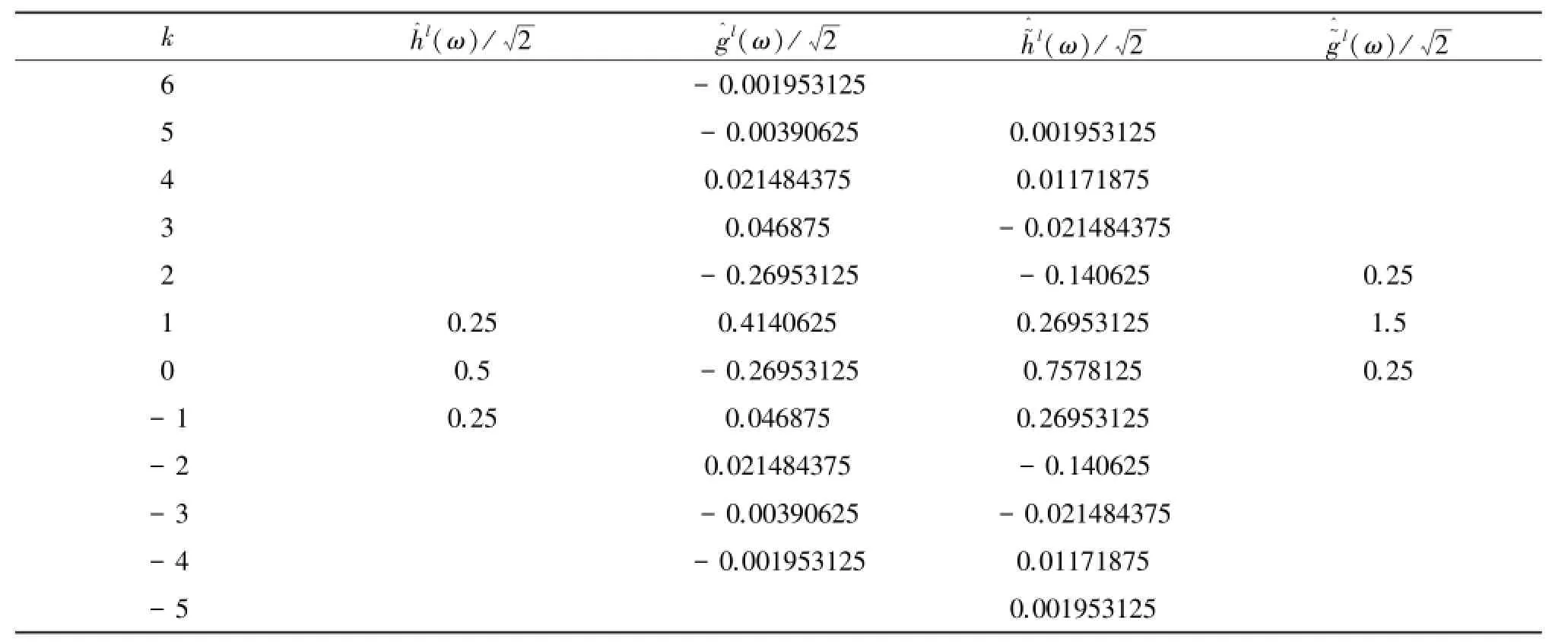
表2 第二次提升二进小波滤波器系数

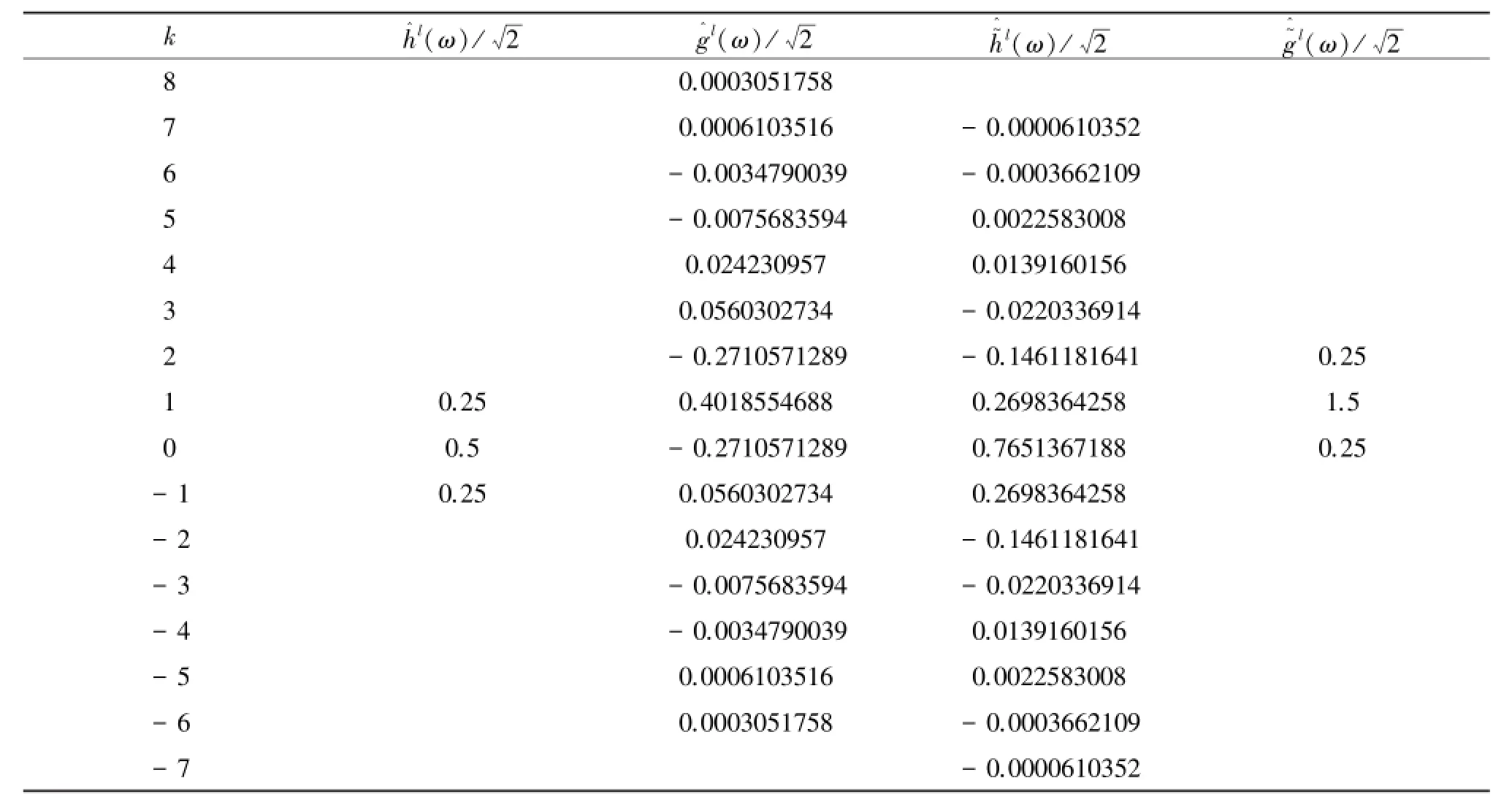
表3 第三次提升二进小波滤波器系数

3.2 利用定义2构造具有6阶消失矩的提升二进小波滤波器

表4 第一次对偶提升二进小波滤波器系数

表5 第二次对偶提升二进小波滤波器系数

表6 第三次对偶提升二进小波滤波器系数

4 结论

文章研究了基于二进提升格式和对偶二进提升格式，构造具有高阶消失矩的二进小波滤波器的方法。通过二进提升格式，以新构造的B－样条二进小波滤波器（r＝2，m＝1）作为初始二进小波滤波器，经过三次提升，构造出新的具有8阶消失矩的提升二进小波滤波器。再以对偶二进提升格式为基础，选择适当的参数，对初始二进小波滤波器进行三次提升，经过大量复杂的计算，推导出具有有限长、线性相位、6阶高消失矩的对偶提升二进小波滤波器。对于提升后的二进小波，其光滑性得到了提高，再根据其平移不变性以及小波变换对信号的适应性。接下来，将把提升后的具有高阶消失矩的二进小波具体应用到图像增强、去噪、压缩、边缘检测，军事电子对抗与武器的智能化，音乐和语言的人工合成，医学成像与诊断，曲线曲面构造、微分方程求解等领域的研究中，期望新构造的二进小波滤波器在实际应用中取得更好的实用效果。

参考文献：

［1］关履泰.小波方法与应用［M］.北京：高等教育出版社，2007：7.

［2］吐尔洪江·阿布都克力木.小波信号处理基础［M］.北京：北京邮电大学出版社，2014：4.

［3］Mallat S.信号处理的小波导引［M］.杨力华，戴道清，黄文良等译.北京：机械工业出版社，2004：11－12.

［4］Mallat S.Wavelet tour of signal processing［M］.Acad－emic Press，1998：34－36.

［5］Abdukirim T，Takano S，Niijima K.Construction of spline dyadic wavelet filters［J］.Informatin Science and Electrical Engineering Journal of Kyushu University，2002，7（1）：1－6.

［6］周先国，李开宇.基于提升小波结合DCT变换的图像去噪研究［J］.计算机技术与发展，2009，（02）：62－65.

［7］吐尔洪江·阿布都克力木.基于自适应二进小波变换的人脸检测方法［J］.计算机工程与应用，2010，46（18）：149－151.

［8］吐尔洪江·阿布都克力木，阿布都许库热·阿布都克力木，张海英.二进小波的构造方法研究［J］.纯粹数学与应用数学，2012，28（2）：149－154.

［9］张海英，姜闪闪，吐尔洪江·阿布都克力木.基于消失矩条件的二进小波滤波器的设计方法［J］.新疆师范大学学报（自然科学版），2008（27）：8－12.

［10］Sweldnes W.The lifting scheme：A construction of second generation wavelets［J］.SIAM Journal on Mathematical Analysis，1997，29（2）：511－546.

［11］Sweldnes W.The lifting scheme：A new philosophy in biorthogonal wavelet constructions［J］.Proceeding of SPIE，1995，2569（6）：68－79.

Based on the Dyadic Lifting Scheme to Construct Dyadic Wavelet Filter with Higher－order Vanishing Moments

WANG Yan－li， Turghunjan·ABDUKIRIM， LU Yan－fei
（Electrical and Information Engineering Department，Xinjiang Normal University，Urumqi，Xinjiang，830054，China）

Article use lifting scheme and dual binary scheme，respectively constructs the new ascension has high 8 order disappear moment binary wavelet filter and high order 6 disappear moment of dual lifting binary wavelet filter.The first step：To construct Mallat B－spline dyadic wavelet（r＝1）expand，through a lot of calculation，experiment repeatedly，finally proved that can get construct new B－spline dyadic wavelet method；The second step：using the new method of constructing binary wavelet，constructs the new B－spline dyadic wavelet（r＝2）as the initial binary wavelet filter，and then based on the binary scheme and dual binary scheme，ascension for three times，respectively is deduced with limited length，linear phase，high order vanished moments of binary wavelet filter and dual lifting binary wavelet filter，and the ascension of the binary wavelet filter which are not avail⁃able through promotion Sweldens scheme to calculate，there can only be described in this article the binary scheme for ascension.

Higher－order vanishing moments；Dyadic lifting scheme；Dyadic Wavelet filter

TN713

A

1008⁃9659（2015）01⁃0016⁃06

2014－11－15

国家自然科学基金资助项目（11261061，61362039，10661010）；新疆维吾尔自治区自然科学基金资助项目（200721104）

汪艳丽（1990－），女，河南信阳人，硕士研究生，主要从事小波分析及其应用的研究。