不同系统接线方式下电压调差率的 整定计算
陈延云 蔡 培 王 锐 戴申华
(1. 国电科学技术研究院,南京 210031; 2. 陆军军官学院,合肥 230031;3. 安徽省电力科学研究院,合肥 230601)
并列运行的同步发电机组通常借助于电压调差率来实现无功功率稳定合理的分配。发电机的电压调差率包括自然调差率和附加调差率。自然调差率又称静差率,现代励磁控制系统稳态增益很大,等于或近似于无差调节,其自然调差率很小,仅靠自然调差率是不能满足机组无功功率分配要求的。为保障机组和电网的安全经济运行,通常需要配置合适的附加调差[1]。若励磁系统调差系数过大,当发电机追踪负荷无功变化时,电网运行电压波动较大,从而影响电压质量,增加电网网络损耗和运行风险;若励磁系统调差系数过小,当电网运行电压微小的变化时,发电机输出更多的无功功率,同时对于并联运行的发电机组将会发生抢无功现象,不利于发电机安全运行[2]。
目前,对于电压调差率整定的基本原则、极性选择方面已有不少文献作过讨论[3-5]。对于机端直接并联运行的发电机组,为了使无功电流能够稳定分配,需要一定的正调差,附加调差系数应为正。当两台及以上发变组单元在高压侧母线并列时,为了机组能够稳定运行,要求各个机组在并列点的调差系数为正调差。对于在高压侧并联的发电机变压器组,由于升压变压器电抗大,发电机无功负荷增大时,高压母线电压下降过多,不利于稳定运行,需要采用负的附加调差系数以补偿变压器电抗。
笔者曾对国内各区域电网大型发电机组励磁系统调差系数的整定现状进行深入调研,发现调差系数的整定工作存在很大的随意性,区域差异较大,定值整定范围宽、管理不规范等问题较突出,有些机组甚至不投入附加调差环节,极大的影响了机组的无功调节能力。为此,对常见系统接线方式下的调差率整定计算进行分析研究,为发电厂提供具有实用价值的整定计算方法,对机组和电网的安全经济运行具有重要意义。
1 发电机-变压器单元接线
目前,大型发电机组一般采用发电机-变压器单元接线方式,通过主变高压侧母线并列,并列点处的调差系数决定了各机组之间的无功分配关系和并列点处电压。这种接线方式中,由于变压器电抗大,发电机无功负荷增大时,高压母线电压下降过多,不利于稳定运行,需采用负的附加调差系数以补偿变压器电抗,加快高压母线的电压响应速度,提高系统电压稳定性。
1.1 整定计算
主变短路阻抗以主变容量为基值,励磁附加调差以发电机额定容量为基值,两者需转换到同一电压等级下的有名值进行计算。主变短路阻抗有名值发电机附加调差有名值为两者相加后得到并列机组在有功电流为零时电压调差率的有名值:
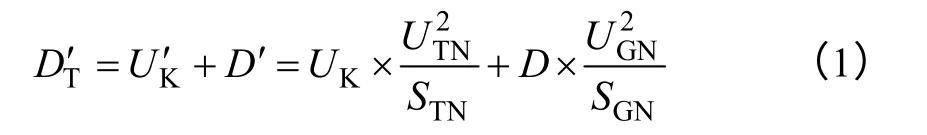
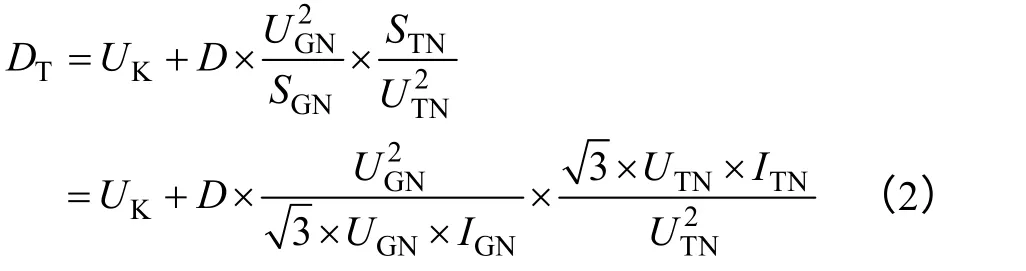
将式(2)化简得到

式(3)就是标准DL/T 843—2010 中给出的电压调差率整定计算公式[6]。
1.2 算例
某火力发电厂总装机容量为2×125MW,发电机通过主变压器接入220kV系统。机组参数如表1所示。
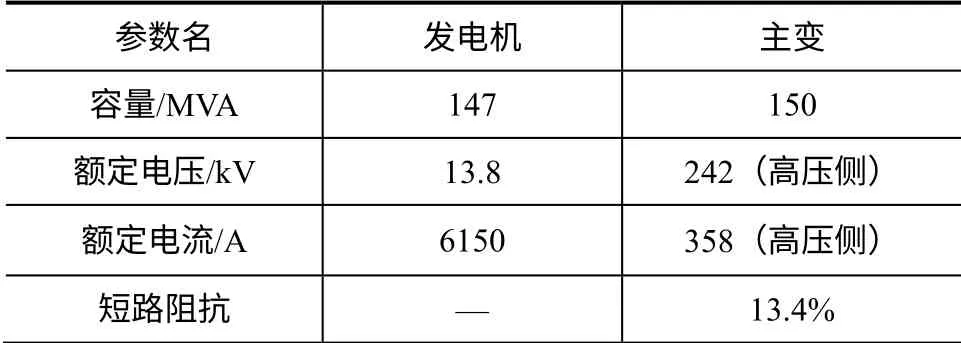
表1 机组参数
设定DT= 5%,根据式(3),计算得到调差率为-8.57%(以发电机额定容量为基值),结果符合工程应用需求。
特别值得一提的是,对于式(3),计算主变压器高压侧并列发电机变压器组的调差率,涉及到主变压器的额定电压和额定电流。主变压器和发电机用同一电压侧的电压和电流,即:主变压器用低压侧的额定电压和电流时,发电机也用同一低压侧的额定电压和电流,主变压器用高压侧的额定电压和电流时,发电机的额定电压和电流应折算到高压侧。
2 经三绕组变压器并列接线
相对于发电机-变压器组单元接线方式,经三绕组变压器并列的接线方式较复杂,调差率设置考虑因素较多。图1中,两台发电机通过两台三绕组变压器分别在高、中压侧并联,高压侧接入电网,中压侧母线为本地负荷母线,无功需求较大。建立该并联方式的等效电路,如图2所示。
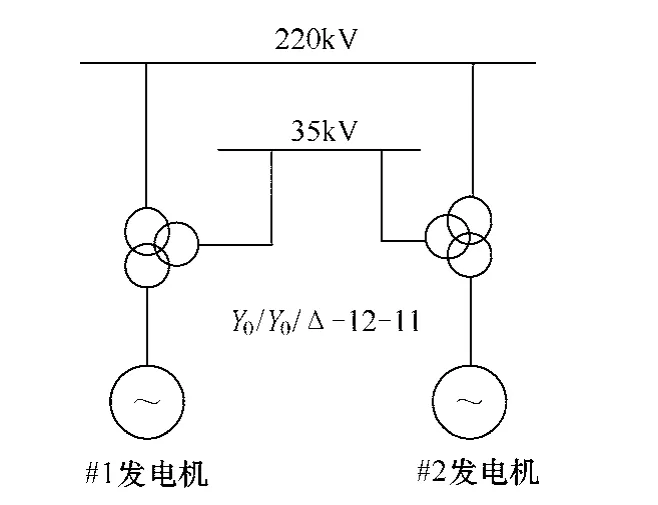
图1 发电机经过三绕组变压器并列运行

图2 等效电路
U11、U21分别为发电机机端电压,U2、U3分别为35kV 和220kV 母线电压,I11、I12、I13、I21、I22、I23分别为发电机和变压器的无功电流。由于变压器的两端电压相角差和电阻很小,所以变压器的电压损耗近似用无功电流在阻抗上的电压降来代替。
根据图2,有以下四个公式成立:
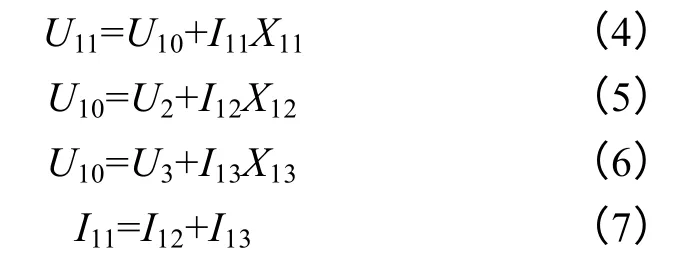
联立式(5)至式(7),消去I12、I13,可得出U10的计算公式:

由式(4)和式(8),可得#1 发电机机端电压:

设#1 机组调差系数为XC1,#2 机组调差系数为XC2,Uref1为励磁调节器给定值,综合考虑调差环节的影响,可得#1 发电机励磁系统输出偏差为
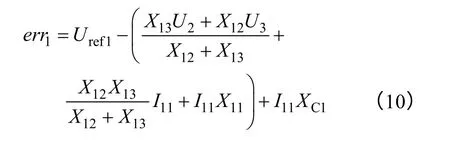
若此时励磁调节器稳态增益为KA,则由式(10),可得出励磁调节器输出的励磁电压EFD1为

同理,可得到#2 发电机励磁调节器输出的励磁电压EFD2为
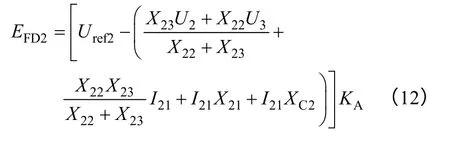
2.1 调差率设置对无功平衡影响分析
取中间量X′1、X′2:

1)设置方式一:XC1<X1′,且XC2<X2′
此时在#1 发电机和#2 发电机之间产生一个环流ΔI,从式(11)可见,EFD1有一个正的增量,同时,EFD2有一个负的增量,而EFD1的增大和EFD2的减小将导致ΔI继续增大,最终出现#2 发电机深度进相,#1 发电机不断发无功的不稳定现象,直至#2发电机低励限制动作或#1 发电机过励限制动作。所以,这种设置是不允许的。
2)设置方式二:XC1>X1′,且XC2<X2′,或XC1<X1′,且XC2>X2′
这里我们以XC1>X1′,且XC2<X2′为例来分析该调差设置的最终结果。如果此时因为某种原因在#1 发电机和#2 发电机之间产生环流ΔI,从公式(11)可见,EFD1有一个负的增量,同时,EFD2也有一个负的增量,两台发电机都在降低电压,这样的结果就是母线电压迅速下降,影响系统稳定运行。所以,这种设置也是不允许的。
3)设置方式三:XC1>X1′,且XC2>X2′
如果此时在#1 发电机和#2 发电机之间产生一个环流ΔI,从公式(11)可见,EFD1有一个负的增量,同时,EFD2有一个正的增量,而EFD1减小和EFD2增大导致ΔI减小,这个环流越来越小,最终两台机组通过平衡无功分配直至稳定,设置合理。
4)整定计算
设期望得到并列点的调差率为X,则XC1、XC2的计算公式为(计算过程应将阻抗值折算到同一个标幺系统下):

如果XC1和XC2设置过大,则励磁电压对无功变化将十分敏感。工程实践和相关分析计算推荐电压调差率整定为3%~5%(以发电机额定无功功率为基值)。
2.2 算例
某热电厂有两台机组通过三绕组变压器并列运行,机组容量63MVA,主变容量63MVA,调差系数初始整定值#1 机组为-3%,#2 机组为-4%。当两台机组并列运行时2 号发电机低励限制动作,1 号发电机无功出力增大,无功分配不稳定。
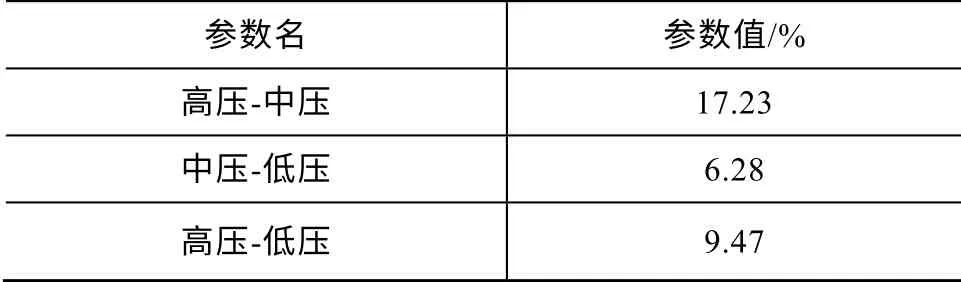
表2 主变压器短路电抗
根据机组参数可计算得到:
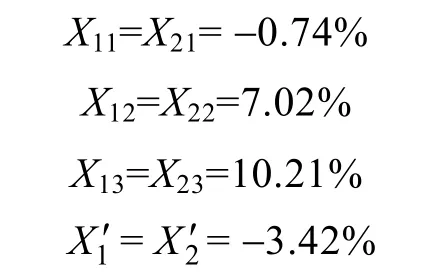
显然属于前文分析的调差设置类型之中的第二种(XC1>1X′,且XC2<2X′),是一种不正确的设置,所以出现了抢无功现象。
为了避免出现抢无功现象,将两台机组的调差系数设置为零,则其等效调差为3.42%,为正调差,更改调差整定值后,机组并列运行时无功调节正常,调差设置正确。
3 结论
并列运行的发电机组,并列点的电压调差率整定需综合考虑发电机的自然调差、附加调差和主变压器压降等因素。对于发电机-变压器单元接线方式,标准DL/T 843—2010 中给出的整定计算公式具有很好的工程实用价值,但计算时主变压器和发电机参数必须采用同一电压侧的电压和电流。经三绕组变压器并列的接线方式,调差率设置不能简单的补偿变压器阻抗,要充分考虑高、中压侧的协调问题。本文针对上述两种系统接线方式提出了整定计算方法,并通过实际应用验证了方法的有效性,希望能为类似接线的机组提供参考。
[1] 竺士章. 发电机励磁系统试验[M]. 北京: 中国电力出版社,2005.
[2] 刘取. 电力系统稳定性及发电机励磁控制[M]. 北京:中国电力出版社,2007.
[3] 方思立,苏为民. 大型发电机调差率整定及调试[J].中国电力,2006,39(8): 12-15.
[4] 张宁,李海翔. 同步发电机组电压调差系数实用整定方法研究[J]. 浙江电力,1996,15(5): 6-9.
[5] 陈继武. 励磁调节器中的调差问题[J]. 华东电力,2002,(10): 35-36.
[6] DL/T 843—2010 大型汽轮发电机励磁系统技术条件[S].
[7] 郭玉恒,徐学琴. 机组并网瞬间抢无功现象分析及定值整定策略[J]. 水电自动化与大坝监测,2011,35(3): 21-24.

