基于磁编码器的电机换向控制

周文胜，张团善，郝永健，孙盟盟，徐 坤

（西安工程大学 机电工程学院，陕西 西安710048）

0 引 言

21世纪以来，随着自动化程度的日益提高，各应用领域对位置传感器的要求也越来越高，传统的位置传感器已经不能满足某些特殊应用领域的要求.旋转变压器体积大、精度低；光电编码器抗震动、抗冲击能力差，无法在尘埃、潮湿等恶劣的环境下工作.尽管在目前市场上的编码器中，光电编码器占有很大的份额，但由于磁编码器的一些独特优点，加上其成本低廉，近年来在机器人、数控机床、测量仪、直接驱动电机和高密度侍服盘读写机等高精度测量和控制领域的应用不断增加，已经成为发展高技术产品的关键技术之一.所以，国内外的很多科研人员把重点转移到了磁编码器的研制上［1］.

磁编码器作为位置传感器，首先必须获得电机转子的位置信息，然后根据电机转子磁极位置进行换相.而目前通常以三相电机为主体，这就需要位置传感器能够识别三相绕组每隔600通断电的要求，使位置传感器能够精确地测量出电机的转动角度，以方便控制电机换向，使电机正常运转［2］.国内外对于电机转动角原始信号的解算方法研究已经非常深入和全面，实际生活中常采用的有跟踪型RDC变换器法，其基本依据是利用反正切法来解码正交余弦电压信号并获得角位置信息，通过数字处理器（DSP）处理信号，然后通过查表法得到电机转动角［3］；还有cordic算法，建立子函数，通过夹逼原理实现电机转角位置［4］；以及三组信号处理法，通过在反正切法的基础上引入第3个信号来处理原始信号，得到电机转角位置［5］.虽然这些方法是可行的，但是需要建立反正切库函数，即需要处理大量数据，执行速度很慢.因此，寻求一种快捷解码算法是集成霍尔磁编码器研究的重点.

本文利用磁编码器的基本原理和特点，通过研究分析目前国内外主流的电机解算算法，即反正切法的理论依据和优缺点，设计出一种正余弦法的解算算法.与反正切法相比它只需建立00→450正余弦函数表即可通过算法实现三相电机的每隔600换向控制，减少了DSP对信号的处理，大大缩短了执行速度.MATLAB仿真处理结果表明，设计的正余弦法电机结算算法可行.

1 磁编码器算法设计

1.1 线性霍尔传感器

磁编码器的基本结构是以连续性线性霍尔传感器为主体，加上滤波电容和温度传感器［6］.线性霍尔元件由自由层和钉扎层组成，应用磁道磁阻技术（TMR）.外部磁场的存在使得自由层和钉扎层的磁极化产生差异，并导致自由层和钉扎层内的电子产生不同的自旋状态，自由层的磁化方向随着外部磁场在同一平面磁通量的极外方向变化；而钉扎层的磁化方向是在生产工艺中被固定的，不会响应外部磁场的变化［7］.因此TMR元件中，在平行状态，即自由层和钉扎层的磁化方向相同时，显示出最低电阻值；在反平行状态，即自由层和钉扎层的磁化方向相反时，显示出最高电阻值.如图1所示.

1.2 算法设计

磁编码器的设计是基于线性霍尔元件旋转一周将产生一个正弦波这一依据来设计的［8］.把两组线性霍尔元件垂直安装形成差分结构，可以有效地消除机械安装偏差和零点漂移所带来的误差，并且使输出幅值增加了一倍，这也是线性霍尔元件安装的基本形式，如图2所示.采用差分安装的线性霍尔元件在一个旋转的外磁场中产生两路差分输出信号A和B［9］.在恒定电压供电下，A和B输出电压和磁场角度的余弦和正弦函数相吻合，其中零角度对应B输出为零，而A输出为最大值情况.因此，在0°～360°之间的每一个角度值都可以由表示余弦和正弦的A和B的输出电压值来定位.

图1 线性霍尔元件原理Fig.1 The principles of linear Hall element

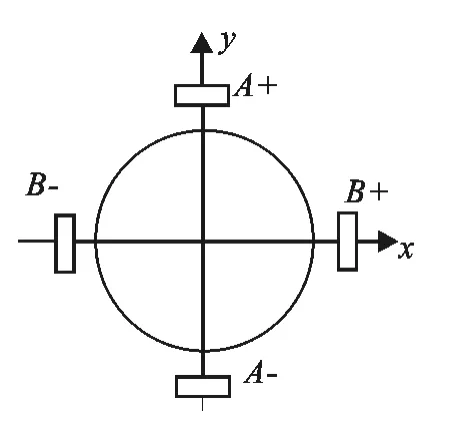
图2 线性霍尔元件差分安装Fig.2 The structure of differential installation on Linear Hall element

1.2.1 采用两组线性霍尔元件求反正切 采用反正切法求电机位置是最常用的方法.根据磁编码器差分安装结构，可以得到式（1）的两组信号.

式中，Umax为线性霍尔元件输出的最大值；UA，UB为两组差分输出信号；θ为电角度.将两者相除并求反正切，可以得到式（2）.

计算反正切一般应用查表法进行，事先根据AD的精度编写好对应的反正切数据表存储在ROM中，计算反正切时，直接读取数组中的对应元素即可.使用这种算法不但原理简单，而且由于将AD采样所得信号相除，所以能消除由于电源电压幅值变化引起的解码误差.但是，由于采用反正切的方法求电机转动位置角度θ，这就牵涉到反三角函数arctan x的函数特性，即其在每接近90°的位置的时候，会使得其测量精度降低，因为根据函数特性，在每接近900的位置时其函数值是无穷大的；同样根据三角函数tanθ的函数特性，其函数值是随着角度增加而趋于无穷大的，这就使得根据式（2）所得到的转角θ的个数也是无穷多，增加了计算θ所需花费的时间，将影响整个磁编码器运算过程.

1.2.2 算法改进设计 为了弥补反正切法的缺陷，解决三角函数固有的属性问题，即正切函数在有些角度函数值无穷的问题.提出了一种基于正余弦函数为依据的正余弦法来得到电机的转角角度［10］.

根据两组差分输出信号UA和UB成正弦和余弦形式，可得图3.根据曲线交点，可以把0°～360°分为8段.每一段使用对应的曲线表得到对应角度值.实际上，每一段查表对应的AD输出值范围是限定在0°→45°范围内的.因此只需编制0°→45°的对应正、余弦值表并存入ROM中.计算角度时候只需根据AD测量数值表即可.

实现过程如下：首先测量两组线性霍尔元件的差分输出值得到UA和UB.然后根据表1判断当前电机位置在哪个区间并得到角度起始值θs.

图3 两组差分输出信号图Fig.3 Two sets of differential output signal diagram

表1 算法区间判断条件Table 1 The interval judgment conditions on algorithm

如表1所示，根据测量所得的两组线性霍尔元件差分输出值UA和UB，可以得出当前电机位置所取的区间.然后根据式（3）

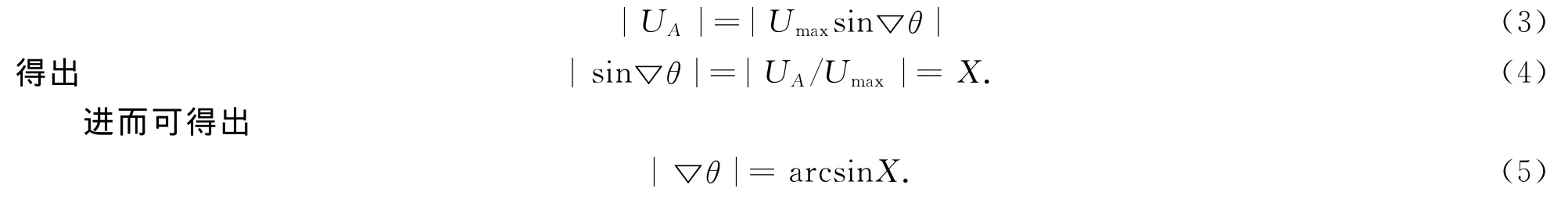
表2 电机当前位置判断条件Table 2 The current position judgement conditions on motor

2 MATLAB仿真

文中使用磁编码器作为电机换向控制中的位置传感器，实现三相电机的换向控制［11］.根据磁编码器两组线性霍尔元件的算法，建立永磁同步电机的仿真系统模型进行MATLAB仿真，仿真系统采用交流永磁同步电机，应用SVPWM算法的Id＝0控制方法［12］.系统仿真图如图4所示.

图4 交流永磁同步电机控制系统仿真图Fig.4 Simulation of AC permanent magnet synchronous motor control system

在此交流永磁同步电机控制系统中，采用10 bit AD采样，所查表范围是0°→45°，表内AD采样值范围为0→512，达到超过0.1bit的分辨率.在仿真系统中输入三相交流电，电机转速为300r/s.通过MATLAB仿真，可以得出定子三相电流和转子角速度，如图5所示.

图5 定子三相电流、转子角速度曲线波图Fig.5 Stator phase current and rotor angular speed wave map

在此永磁同步电机仿真系统模块中，位置传感器采用磁编码器完成，算法根据文中涉及的正余弦法实现.磁编码器得到的角度与直接编码器得到的角度对比如图6所示（均为电角度）.编码器是累加方式，在超过360°之后继续增加，因此，减去n×360°（n为电机转过的圈数）之后与使用三组线性霍尔元件测得的角度相同.编码器和磁编码器输出对比如图6所示.

通过图6可以看出，文中的磁编码器的算法设计，即用正余弦法来标记电机转子转动角度的设计是合理的.同时也看出磁编码器电机角度控制算法方便，它比直接应用编码器进行累加角度的方法快捷方便，数据量也少.

3 结束语

本文从电机换向控制的方法入手，先比较传统的机械换向和目前常用的电子换向中的优缺点，提出了一种基于磁编码器为位置传感器的电子换向的方法.根据磁编码器作为位置传感器的工作原理和结构特点，设计出一种正余弦法的电机换向控制模型.并且在MATLAB中建立了一套基于磁编码器的永磁同步电机模型并进行仿真，结果表明，定子三相电流和转子角速度波图完整，系统运行稳定，证明了本文磁编码器的算法设计是可行的，能够快速得到电机的转角位置.

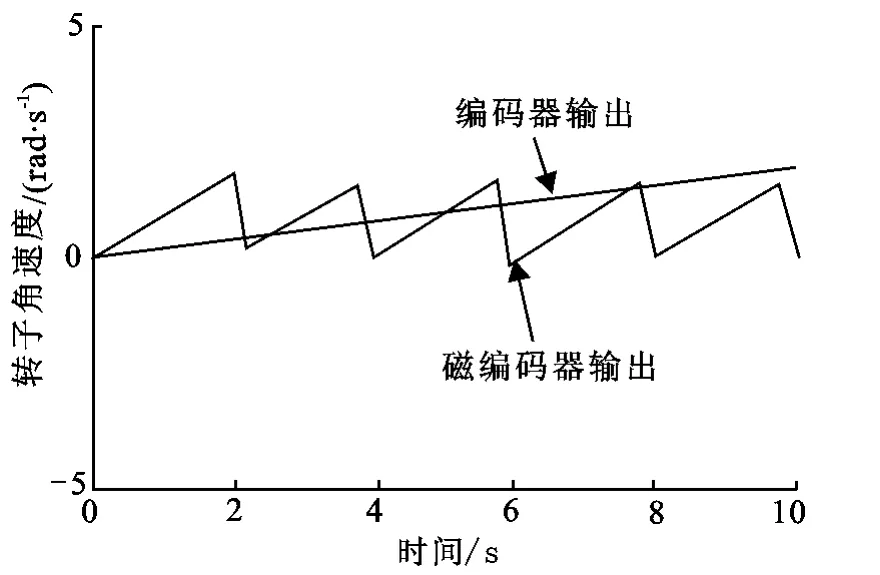
图6 编码器输出和磁编码器输出对比Fig.6 The contrast of encoder output and magnetic encoder output

［1］ 廖红伟，杨晓非.磁旋转编码器的发展及其应用［J］.信息记录材料，2003，4（1）：40－44.LIAO Hongwei，YANG Xiaofei.The development and application of magnetic rotary encoder［J］.Information Recording Materials，2003，4（1）：40－44.

［2］ 叶平，孙汉旭，贾庆轩，等.磁编码器在直流无刷电机换相与控制中的应用［J］.仪表技术与传感器，2007，1（1）：38－41.YE Ping，SUN Hanxu，JIA Qingxuan，et al.Application of magnetic encoder in phase commutation control of BLDCM［J］.Instrument Technique and Sensor，2007，1（1）：38－41.

［3］ 吕德刚.集成霍尔磁编码器的研究［D］.黑龙江：哈尔滨工业大学，2009：1－4.LYU Degang.Research of integrated hall magnetic encoder［D］.Heilongjiang：Harbin Institute of Technology，2009：1－4.

［4］ 吕德刚，李铁才，杨贵杰.高性能磁编码器设计［J］.仪器仪表学报，2006，27（6）：1346－1350.LYU Degang，LI Tiecai，YANG Guijie.High performance magnetic encoder design［J］.Chinese Journal of Scientific Instrument，2006，27（6）：1346－1350.

［5］ 于非，赵继敏，罗响.磁编码器算法分析和研究［J］.微特电机，2011，10（1）：20－25.YU Fei，ZHAO Jimin，LUO Xiang.Analysis and research of the algorithm of magnetic rotary encoder［J］.Micro Motor，2011，10（1）：20－25.

［6］ 宋玉琴，朱紫娟，姬引飞.多传感器信息融合的智能故障诊断［J］.西安工程大学学报，2014，28（5）：568－573.SONG Yuqin，ZHU Zijuan，JI Yinfei.Intelligent fault diagnosis strategy of multi－sensor data fusion［J］.Journal of Xi′an Polytechnic Unversity，2014，28（5）：568－573.

［7］ 郝双辉，刘勇，周春蛟，等.基于标定原理的单磁极编码器设计［J］.南京理工大学学报，2005，144（29）：226－228.HAO Shuanghui，LIU Yong，ZHOU Chunjiao，et al.Design of single－pole magnetic encoder based on calibration［J］.Journal of Nanjing University of Science and Technology，2005，144（29）：226－228.

［8］ 曾一凡，高珊，张炳义.基于信号运算和插值原理的磁轴角编码器［J］.仪表技术与传感器，2008，12（1）：49－51.ZENG Yifan，GAO Shan，ZHANG Bingyi.Magnetic rotary encoder design based on signal operation and interpolation theory［J］.Instrument Technique and Sensor，2008.12（1）：49－51.

［9］ 拓小明，李云红，刘旭，等.基于Canny算法与阈值分割的边缘检测算法［J］.西安工程大学学报，2014，28（6）：745－749.TUO Xiaoming，LI Yunhong，LIU Xu，et al.The edge detection algorithm based on Canny operator and threshold segmentation［M］.Journal of Xi′an Polytechnic University，2014，28（6）：745－749.

［10］ 江晓光.线性霍尔传感器在永磁同步电动机矢量控制器中的应用［J］.微特电机，2010，38（4）：73－74.JIANG Xiaoguang.Application of linear hall sensor in PMSM controller［J］.Micro Motor，2010，38（4）：73－74.

［11］ 郝双辉，刘勇，刘杰，等.基于查表原理的单对磁极编码器研制［J］.中国电机工程学报，2006，26（19）：165－168.HAO Shuanghui，LIU Yong，LIU Jie，et al.Design of single pair－pole magnetic encoder based on looking－up table［J］.Proceedings of the CSEE，2006，26（19）：165－168.

［12］ 王爽，李铁才，王治国.基于CORDIC算法的高分辨率磁编码器设计［J］.微电机，2009，42（8）：1－5.WANG Shuang，LI Tiecai，WANG Zhiguo.Design of high resolution magnetic encoder based on CORDIC algorithm［J］.Micromotors，2009，42（8）：1－5.