内蒙古大兴安岭地区偃松生长规律

庄会霞，刘琪璟，孟盛旺，贾全全，邓留宝

（1. 北京林业大学 林学院，北京 100083；2. 内蒙古自治区满归林业局，内蒙古 满归 022363）

树木生长及其生长的速度，一方面受树木自身遗传因素的影响，另一方面受外界环境条件的影响。其中，树高是指树干根颈处到树干梢顶的垂直高度。将树干根颈处到梢顶的距离称之为树干长度，简称伸长生长量。当树干直立生长时，树高和树干长度相等；当树干倾斜生长时，树高小于树干长度。

偃松Pinus pumila为松科松属中少有的常绿灌木，又称爬地松、矮松等。灌木状小乔木。分枝较多，冠幅大的可达5～10 m。雌雄同株。雄花紫色，球果紫褐色。花期6～7月，果期次年9月。阳性树种，稍耐庇荫，耐寒抗风。在中国分布在北纬52 °以北地区。内蒙古自治区、黑龙江省（大兴安岭、小兴安岭及张广才岭），吉林省（长白山）、辽宁省均有分布[1]。由于生境不同，其形态特征有所变化[2]，可区分为3种类型：偃松矮曲林，偃松兴安落叶松林和石质台地偃松林[3]。在高海拔，与高山植物（小灌木和草本）混交；在低海拔，作为林下植被物种（下木），与高冠植物混交。

偃松是高山高寒地带维持生态系统结构和功能的重要树种，同时偃松作为我国东北地区主要食用树种资源之一[4]，具有重要的经济价值，对我国丘陵山区社会主义新农村建设具有不可缺少、不可替代的作用[5]。此外，偃松还具有重要的观赏价值和野生动物保护价值等[1,6-8]，但我国关于该树种生长特性方面的研究还很少。本研究以偃松个体为研究对象，采用树干解析法，分析了偃松在2种生境条件下的树干长度生长、直径生长和年轮生长规律，并建立了生长过程模型，旨在研究不同生境下偃松生长状况。

1 研究地区与研究方法

1.1 研究地概况

研究地点位于内蒙古自治区满归林业局，处于大兴安岭北部，地理坐标为 E120°12'～ 122°55'，N50°20'～52°30'。该区属寒温带森林气候，并具有大陆性季风气候的某些特征，冬季寒冷漫长，生长期短。年降水量350 mm～450 mm，主要集中在6～8月份，无霜期平均为90 d，气温日较差大，平均气温－5.3 ℃，极端最低气温－58 ℃，年较差47.4 ℃，日较差20 ℃，结冻期210 d以上，境内遍布永冻层，个别地段30 cm以下即为永冻层，土壤以棕色针叶林土为主。

调查样地有两处，位于不同海拔。山脊（1 100 m）样地位于满归林业局的高地林场，为偃松单优群落，偃松密度较高，乔木层伴生少量生长不良的白桦Betula platyphylla和兴安落叶松Larix gmelinii。林下植被有岩高兰Empetrum nigrumvar.japonicum、细叶杜香Ledum palustre和越桔Vaccinium vitis-idaea等。谷底（650 m）样地为杜香-偃松-兴安落叶松林，位于满归林业局的王八沟，乔木层为兴安落叶松，灌木层为矮小的细叶杜香，地表层密生苔藓，偃松在林下呈团状分布，偃松灌丛间距离较远。

1.2 研究方法

1.2.1 样品采集与测定

偃松为多树干丛生，呈半匍匐状。每丛树干数量3～19个。调查中每个树干视为一个单株。偃松分布在环境比较严酷的地段，破坏性采样对群落影响较大，管理部门对采样有严格限制。所以本研究以最小限度干扰的原则，分别在山脊偃松矮曲林和谷底偃松落叶松林中各采伐5株偃松，从基部至梢顶，每50 cm截取圆盘，测定各圆盘的带皮直径和树干总长度。由于偃松树干倾斜或匍匐，难以准确测定树高，本研究测定的是树干长度。在谷底和山脊分别采集圆盘48和61个，带回北京的实验室进行处理测定。

由于偃松直径生长缓慢，年轮很窄，有时肉眼难以分辨，故对采集的圆盘用电动砂轮打平，然后依次用300目和600目砂纸打磨。用LINTAB年轮测定仪测定年轮宽度（精度0.01 mm），每个圆盘测定4个方向的年轮宽度并计算平均值。圆盘的年轮数即为从该位置到梢顶生长所需时间。采样时间为2013年6月份，生长期尚未结束，最外层当年生长部分为不完整年轮。圆盘是在风干条件下测定的。为了和野外调查数据保持一致性，本研究测定了木材径向干缩率，方法是，将经过打磨的鲜样圆盘用600 dpi的分辨率扫描，然后将圆盘风干，再次扫描。利用图像处理软件分别测定鲜样和风干圆盘相同位置的年轮宽度，计算干缩率。试验过程中发现，该树种的木材径向干缩率略大于切向干缩率，因为所有圆盘没有沿半径方向开裂的现象，相反有心材和边材之间略有因收缩而形成弧形裂隙的情况。本研究仅考虑径向干缩因素，忽略切向和径向干缩。根据测定的干缩率，对测定的年轮宽度进行校正，理论上复原为鲜样状态的宽度值。

本研究的生长过程包括径向和纵向伸长生长，其中径向生长包括年轮生长和带皮直径生长，带皮直径为各树盘的实测鲜样带皮直径，伸长生长即树干长度生长。

1.2.2 模型建立

树木生长过程模型可以分为理论模型和统计模型，后者也叫经验模型，而代表性的理论模型是逻辑斯底模型，或简称 “S”型曲线[9-11]。由于偃松为乔木状灌木，可以借鉴乔木树种的生长模型，并根据偃松自身生长特点，分别选择6种树高生长模型、5种直径生长模型和5种树高-基径模型进行拟合，并对各种模型的优劣进行评价，在此基础上选择最佳模型。各模型表达式如下所示，其中，L指树干长度，单位为cm；D指直径，单位为mm；A指年龄，单位为年（a）；a，b，c为模型参数。判断模型优劣的指标有平均绝对值误差（Mean Absolute Error，MAE）、均方误差（Mean Square Error，MSE）和相对误差百分数（Relative Error，RE）以及决定系数R2。选择R2较大，MAE、MSE、RE%较小的模型为最优模型。公式（1）～（4）中，分别代表观测值、观测值的均值和模型预测值。

模型评价指标：

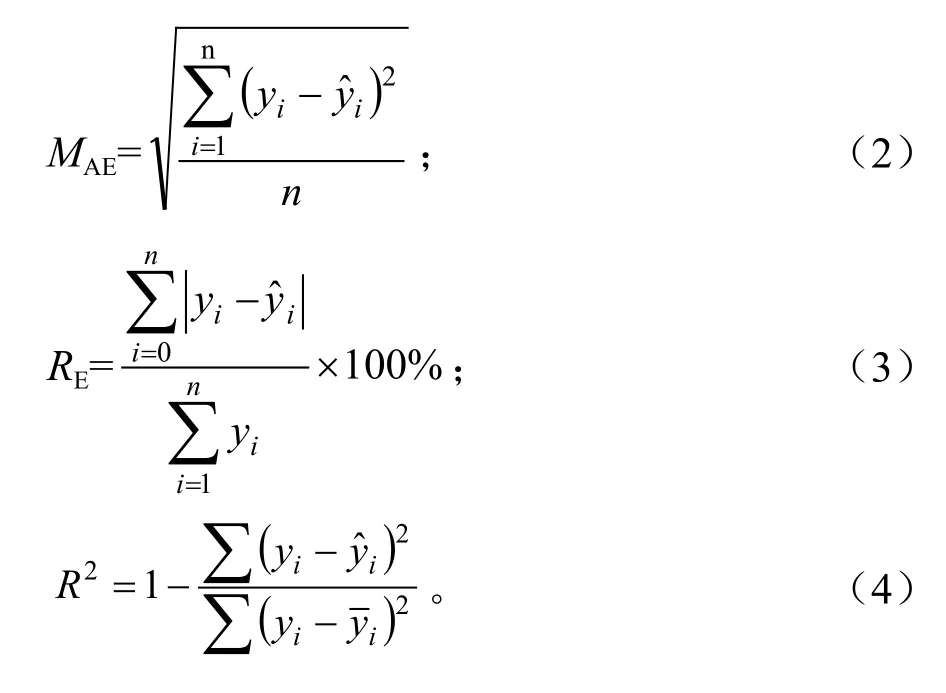
2 结 果

2.1 数据描述

谷底5株样木基径69.58～99.85 mm，平均83.36 mm；干长379～580 cm，平均491 cm；年龄86～98 a。山脊5株样木基径92.08～154.45 mm，平均127.62 mm；干长566～702 cm，平均612 cm；年龄67～71 a。根据调查数据分析了树干长度与基径大小的关系，其中谷底样木数18株，基径范围24.56 mm～99.85 mm，均值为50.21 mm；干长193 cm～580 cm，均值为326 cm。山脊样木11株，基径63.00 mm～154.45 mm，均值为116.10 mm；干长390 cm ～702 cm，均值为576 cm。

不论是在谷底还是在山脊，偃松样木均具有相似的树干形状（图1）。从树干基部至梢顶，树干直径不断增大。但是，偃松树干基部附近的直径随位置增高有增大的现象，主要是因为地表附近树干的树皮部分脱落或者完全脱落。从距基部1 m左右开始，树干直径随着距基部的距离增大为急剧减小。

图1 偃松树干直径与距基部距离的关系Fig.1 Relationship between tree main stem diameters and their distance of from cut point to basal portion for five P. pumila trees in ridge and valley

2.2 树干伸长生长

谷底伸长生长各模型的决定系数R2在0.92～0.97之间，平均绝对误差（MAE）为22.09～33.92 cm，均方误差（MSE）为26.81～41.53 cm，相对误差百分数（RE%）为7.99～12.28%（表1）。其中线性模型、幂函数模型和二项式模型拟合效果较好，模型的平均绝对误差，均方误差和相对误差百分数都较小。由于二项式模型各评价指标值都较低，故二项式模型为最优模型。山脊树干伸长生长各模型R2为 0.93～ 0.97，MAE为 23.95～ 37.22 cm，MSE为29.62～31.72 cm，RE%为7.16～11.14%，拟合效果均较好（表2）。但二项式模型的R2最大，MAE、MSE和RE%%最小，故二项式模型为最优模型。图2为谷底和山脊偃松树干伸长生长模型拟合结果，图3展示了树干伸长生长速率随着树干长度的变化规律，从中可以看出山脊偃松伸长生长较谷底的快。

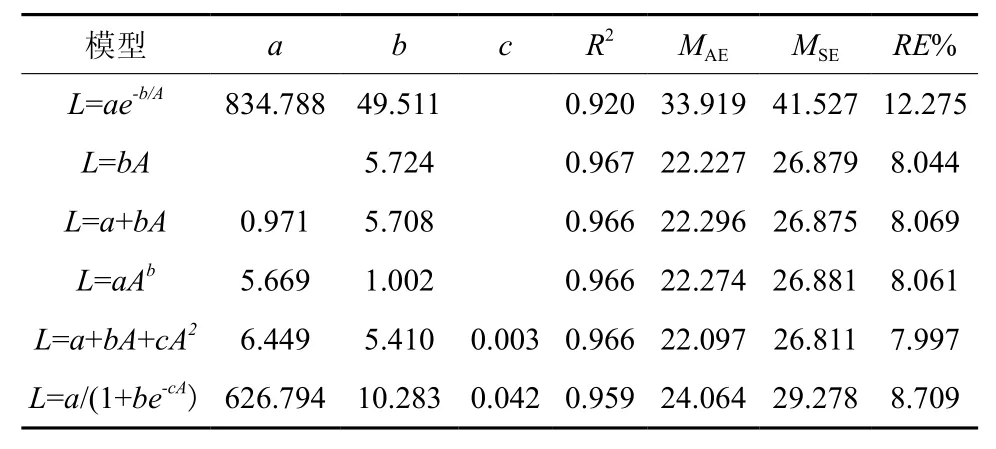
表 1 谷底树干伸长生长模型参数和评价指标†Table 1 Model parameters and evaluation indexes for tree stem elongation in valley

表 2 山脊树干伸长生长模型参数和评价指标Table 2 Model parameters and evaluation indexes for tree stem elongation in ridge

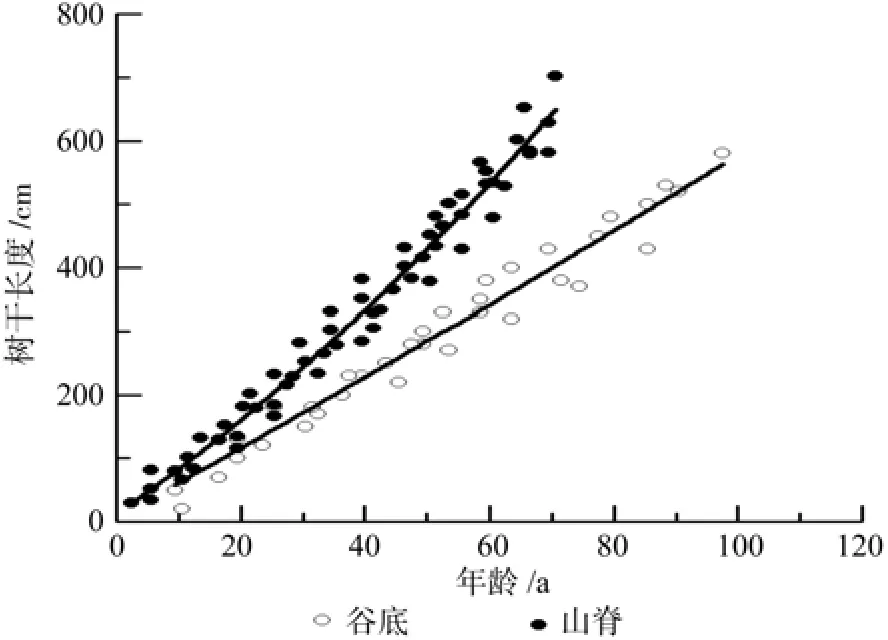
图2 不同生境的偃松伸长生长Fig.2 Stem elongation in different sites

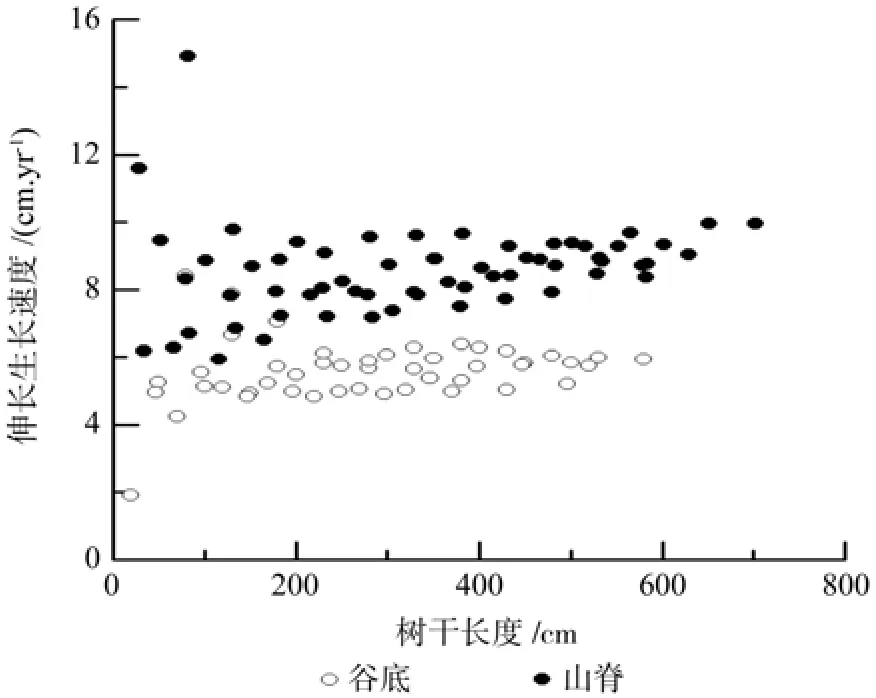
图3 树干伸长生长速率Fig.3 Stem elongation rate

2.3 偃松直径生长

谷底偃松直径生长各模型决定系数为0.89～0.93，MAE为 4.92～ 7.12 mm，MSE为 6.35～8.12 mm，RE%为9.43～13.66%，拟合效果均较好，但以幂函数模型拟合较好最好（表3）。山脊偃松直径生长各模型的决定系数均大于0.84，MAE为10.26～13.93 cm，MSE为14.53～17.01 mm，RE%为14.28～19.39%，拟合效果均较好，但以二项式函数拟合效果最好（表4）。直径生长拟合结果如图4所示，图5为直径生长速率随直径的变化情况，由此可以看出山脊偃松直径生长较快。

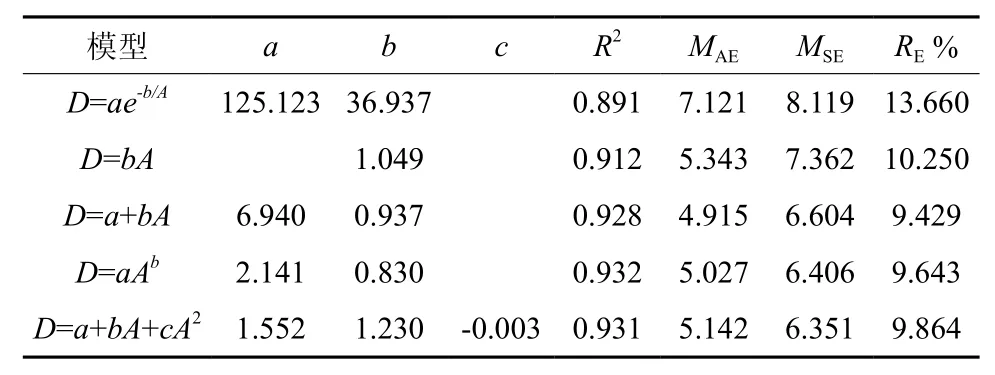
表 3 谷底直径生长模型参数和评价指标†Table 3 Model parameters and evaluation indexes for stem diameter growth in valley

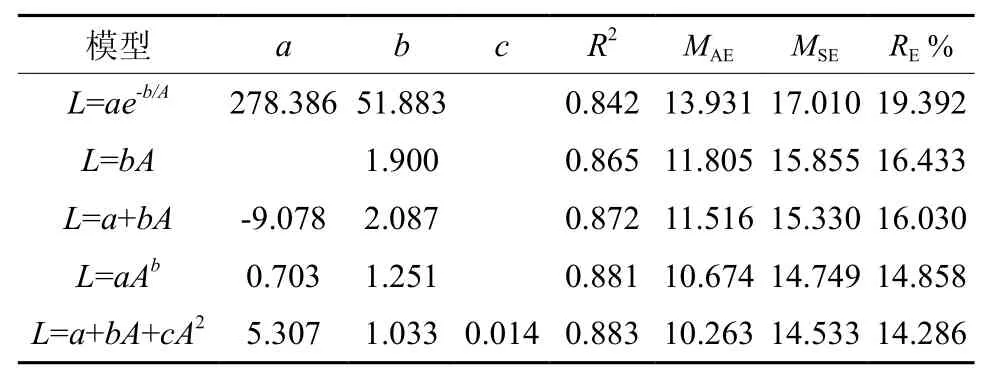
表 4 山脊直径生长模型参数和评价指标Table 4 Model parameters and evaluation indexes for stem diameter growth in ridge

图4 偃松直径生长Fig.4 Diameter growth of P. pumila

图5 偃松直径生长速率Fig.5 Diameter growth rate

2.4 年轮生长

按照测树学的定义，连年生长量是逐年测定的半径生长量即实际年轮宽度，而平均生长量则是任意时刻的累积生长量（即总生长量或半径）与该时刻的年龄之比。谷底和山脊单个年轮宽度范围分别为0.06～1.84 mm和0.14～2.89 mm，平均分别为0.44 mm和0.84 mm。在谷底，年轮宽度平均生长量变化区间为为0.17～0.46 mm/a，平均为0.43 mm/a；年轮宽度连年生长量为0.13～0.67 mm/a，平均为0.41 mm/a。在山脊，年轮宽度年均生长量为0.48～0.98 mm/a，平均为0.84 mm/a；连年生长量为0.46～1.40 mm/a，平均为0.86 mm/a。山脊偃松年轮宽度的平均生长量和连年生长量均高于谷底的（图6）。不同生境的偃松生长趋势都显示，在个体形成初期生长速度较快，有的年份半径生长量（即年轮宽度）可超过1.00 mm（图6）。假设2013年和2012年的年轮宽度相同，谷底2013年年轮宽度为0.32 mm（至调查时尚未结束生长），2012年为0.49 mm，那么2013年调查时约完成当年可能生长量的66%（0.32/0.49）；山脊2013年和2012年的年轮宽度分别为0.47 mm和0.95 mm，2013年调查时约完成了当年50%(0.47/0.95)的生长。

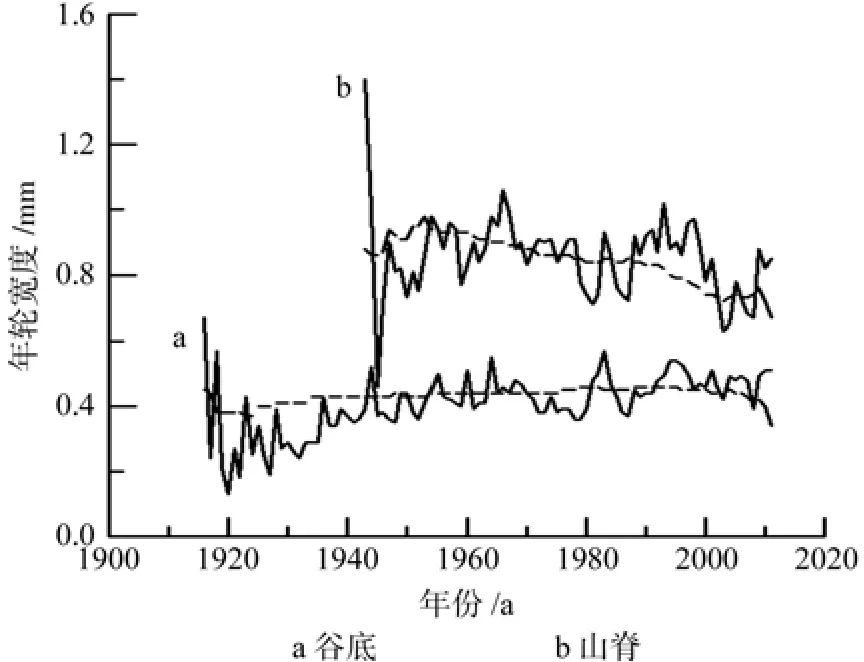
图6 年轮平均生长量和连年生长量Fig.6 Mean annual increment (dotted line) and current annual increment (solid line) of annual ring

2.5 树干长度与基径的关系

谷底偃松树干长度-基径回归模型的决定系数均在0.95以上，其中以幂函数模型拟合效果最优（表5）。山脊干长-基径模型的决定系数均大于0.81，其中以二项式模型拟合效果最优（表6）。直径小70 mm时，谷底和山脊偃松的树干长度接近，但当基径大于70 mm时，谷底偃松的树干长度大于山脊偃松的树干长度（图7）。山脊树干长度增长速率随着直径的增大而减小，越来越平缓，符合树高生长的一般规律。

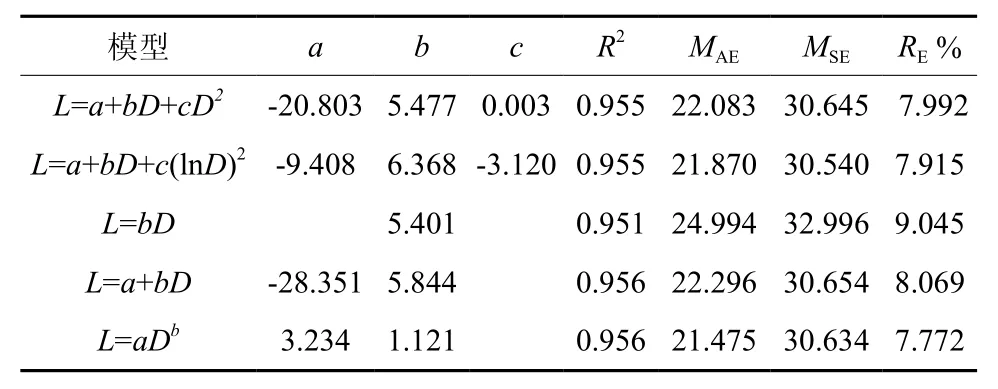
表 5 谷底树干长度-直径模型参数和评价指标†Table 5 Stem length-basal diameter model parameters and evaluation indexes in valley

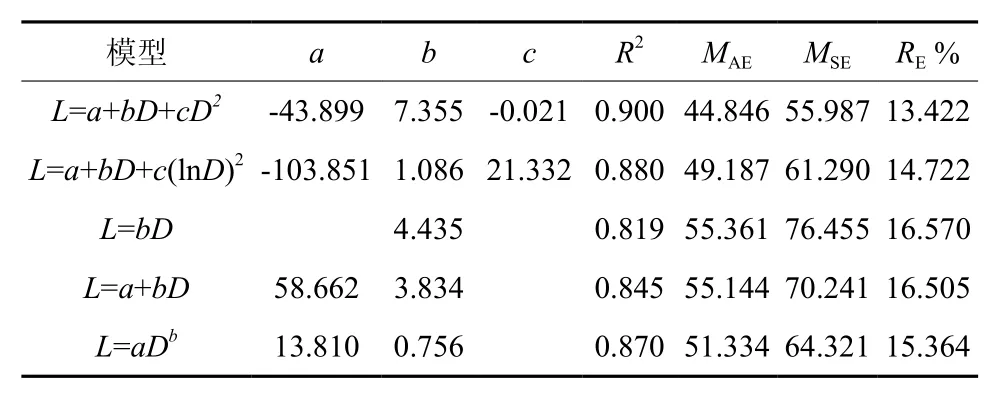
表 6 山脊树干长度—直径模型参数和评价指标Table 6 Stem length-basal diameter model parameters and evaluation indexes in ridge

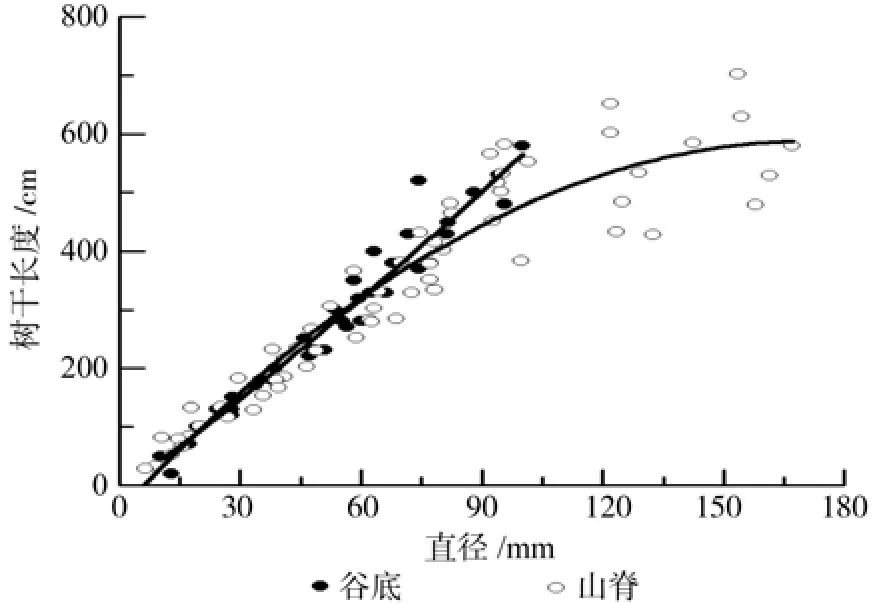
图7 偃松伸长生长与基径的回归关系Fig.7 Regression relation of stem elongation and basal diameter

3 讨 论

若伸长生长呈一元线性函数变化（不含截距），则谷底和山脊偃松树干伸长生长速率分别为5.72和8.72 cm/a，山脊树干伸长生长速率较大（表1，表2）。如图3所示，偃松生长初期伸长生长速率变化幅度较大，但当树干达到一定长度时，谷底生长速率稳定在5.7 cm/a左右，山脊在8.5 cm/a左右，与线性模型的斜率接近。山脊偃松伸长生长速率波动较大，关于密度对树高生长的影响，尽管很多研究在不同情况下取得的不同的结论，但过密时种内竞争较大，个体间高生长差异较大，调查时发现山脊偃松矮曲林很密。整体上，山脊偃松伸长生长较快，可能是因为谷底落叶松透射到林下的太阳辐射总量小于山脊太阳辐射总量，碳同化量较低，生长较慢[12]。其次，还与树种自身的遗传因素有关，据知偃松寿命可达250 a[13]，而树木生长有阶段性，有时生长速率随着林龄增大而降低[14-15]。在日本，由于受温度的和强风影响，山脊（2 850 m）的干长低于谷底（2 500 m）的[16]，海拔相差350 m。偃松树冠长度和树高随着海拔降低而增大[17]，树干长度随着海拔的升高而降低[18]。本研究两海拔远低于以上研究的。一般而言，在一定海拔范围内，随着海拔上升，树种生长加快；到达生长上限后，生长随海拔上升而减缓。高生长速率随着树高增大而减小[19]。偃松伸长生长速率随树干长度的增大而增大[16,20]。但满归地区偃松伸长生长速率随着树干长度的增大而减小，最后保持稳定，可能是因为基部树干被掩埋的速率与伸长生长达到了一种动态平衡。

偃松直径生长模拟结果显示，谷底直径生长各模型拟合效果优于山脊的，决定系数高，评价指标值均较低（表3，表4）。如果直径呈一元线性函数（不含截距）变化，则谷底和山脊偃松直径生长速率分别为1.05 mm/a和1.90 mm/a（表3，表4），山脊偃松直径生长较快。山脊处偃松直径生长速率波动幅度非常大，随直径增大呈现先减小后增大的趋势（图5），且波动较大。可能是由于在密闭的矮曲林内，个体生长受临近木密度的影响较大，临近个体死亡和新的个体的产生都会影响目标个体的生长，而在兴安落叶林中，偃松灌丛之间距离较远，而丛内个体向外辐射生长，种内几乎不存在竞争，且落叶松对林下的影响相对稳定，所以偃松直径生长速率比较稳定。但是，谷底偃松直径生长较慢，因为在落叶松林中，上层树种对偃松生长有一定的抑制作用[21]。生长季节的降水量显著影响直径生长[22]。径向生长随着土壤温度的上升而加快，土壤温度高将促使养分矿化速度加快，高土壤温度和低养分有效性或者低土壤温度和高养分有效性有利于树木的生长[23]。年轮宽度与年降水量和雨季降水量密切相关[24]。因此，上层树种兴安落叶松通过减少透射到林冠下层的太阳辐射量和降水量限制了下木偃松的径向生长。水分和温度是影响高海拔树种的直径生长的主要因素[25]。但在山脊处，偃松矮曲林较密，减少了地面辐射，从而使土壤温度较高，加快了养分的矿化，有利于树木的生长。

谷底树干长度-直径模型参数和评价指标均优于山脊的（表5，表6），且随着直径的增大，山脊偃松树干长度波动较大（图7），这与山脊处环境变化较大有关，而谷底落叶松林下的气候条件基本不变。目前普遍认为树高与胸径的相关关系指数（即异速生长模型中的b值）约为2/3，但谷底偃松的该指数值远高于2/3，这是由于在不同树种间，该值差异性较大，且基径-茎长和胸径-树高关系可能存在差异[26]。日本本州岛中部（海拔2 595～3 192 m）偃松干长随着基径增大呈线性变化[27]，L=-13.672+4.382D。当基径小于135 mm时，本州岛地区的偃松干长低于大兴安岭地区的；当基径大于135 mm时，高于大兴安岭山脊偃松矮曲林的（图8）。胸径-树高的异速生长在一定程度上受到临近木的影响。关于静态胸径-树高关系的研究并未明确说明是年龄效应还是临近木效应影响了二者的关系[28]。因此，关于二者之间的关系有待进一步的研究。

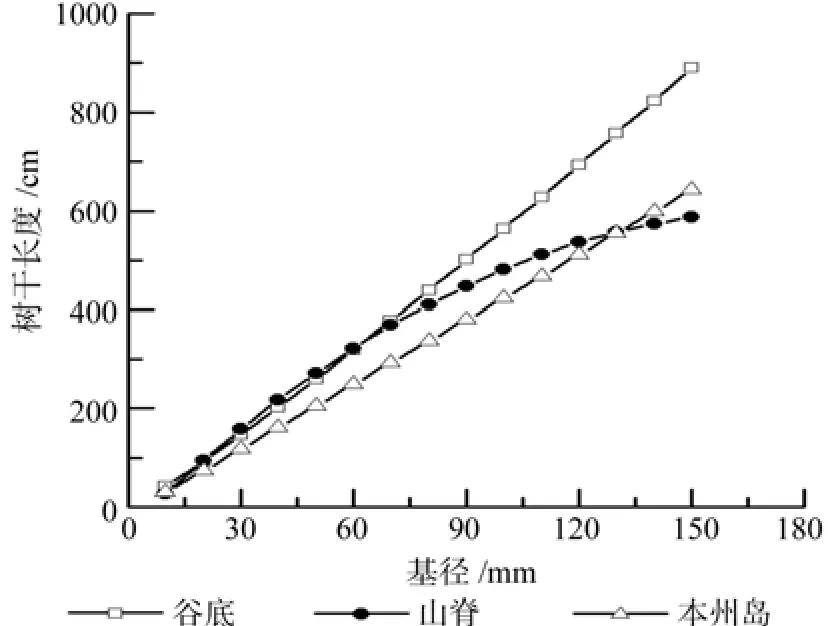
图8 不同海拔的理论干长与基径的关系Fig.8 Relationship between theoretical stem length and basal diameter at different altitudes

生长模型是定量研究树木生长过程的有效手段。Mitscherlich方程、Logistic方程和Richards方程作为常用的理论方程，因其拟合效果好且参数具有明确的生物学意义，故被广泛应用。Richards方程作为一种易于弯曲的生长函数，其适用性更为广泛。而Logistic方程更适于红松等生长较缓慢的树种，Mitscherlich方程适于速生树种[29]。Logistic方程对兴安落叶松高生长的拟合效果好[30]。但这3个模型对偃松单木生长的拟合效果较差，尤其是Richards，可能与树种本身的生长特性有关。为了减小对群落的破坏，本研究采集的样本数量有限，并未对模型进行检验。基于所收集的数据样本有限，本研究中并没有将立地条件、林分密度等作为影响因子，而偃松径向生长和纵向生长都与以上因素有关，随着数据不断地充实以及完备，一定会将上述相关性进行进一步的研究。

4 结 论

谷底和山脊偃松树干伸长生长最优模型均为二项式模型。谷底直径生长以幂函数模型拟合效果最好，山脊直径生长以二项式模型为最优模型。幂函数模型对谷底树干长度与基径关系的拟合效果较好，二项式模型对山脊树干长度—直径回归关系拟合效果较好。

无论是纵向生长还是径向生长，偃松在山脊的生长较谷底的快，一方面与其自身生长特性有关，另一方面又受林分密度、立地条件、气候条件等因素的影响，谷底偃松的生长还受到冠层树种兴安落叶松的影响。

[1] 范瑞红, 栾连航, 倪 薇, 等. 偃松引种研究[J]. 林业科技,2009, (6): 5-7.

[2] 赵垦田, 李玉昌, 张桂玲. 大兴安岭偃松林资源及其开发利用与保护[J]. 国土与自然资源研究, 1997, (2): 55-59.

[3] 《内蒙古森林》编辑委员会编著.内蒙古森林[M]. 北京:中国林业出版社, 1989, 151-154.

[4] 沈海龙, 林存学, 杨 玲, 等. 东北林区经济林树种资源概况、存在问题与发展对策[J]. 经济林研究, 2013, 31(2): 160-166.

[5] 何 方, 张日清, 汪灵丹. 经济林在中国社会主义新农村建设中的作用[J]. 经济林研究, 2008, 26(1): 93-97.

[6] 尹 君, 曹海波, 崔克城, 等. 偃松的观赏药用价值及加工利用[J]. 特种经济动植物, 2002, (2): 29.

[7] 陈国富, 韦昌雷, 朱万昌, 等. 偃松及其价值[J]. 特种经济动植物, 2000, (1): 28-32.

[8] 吴 刚, 冯宗炜. 中国主要五针松群落学特征及其生物量的研究[J]. 生态学报, 1995, 15(3): 260-267.

[9] 刘 平, 马履一, 贾黎明, 等.油松人工林单木树高生长模型研究[J]. 林业资源管理, 2008, (5): 50-56.

[10] 邢黎峰, 孙明高, 王元军. 生物生长的Richards模型[J]. 生物数学学报, 1998, 13(3): 348-353.

[11] 段爱国, 张建国, 童书振. 6种生长方程在杉木人工林林分直径结构上的应用[J]. 林业科学研究, 2003, 16(4): 423-429.

[12] Hoch, G., Popp, M., Körner, C. Altitudinal increase of mobile carbon pools in Pinus cembra suggests sink limitation of growth at the Swiss treeline[J]. Oikos, 2002, 98: 361-374.

[13] 徐化成.中国大兴安岭森林[M]. 北京: 科学出版社, 1998.

[14] Daniel P. Bebber, Sean C. Thomas, William G. Cole,et al.Diameter increment in mature eastern white pine Pinus strobus L. following partial harvest of old-growth stands in Ontario,Canada[J]. Trees, 2004, 18: 29-34.

[15] 刘发林, 曾思齐, 刘 玉, 等. 臭松次生林生长规律研究[J].中南林业科技大学学报, 2014, 34(7): 45-49.

[16] Takahashi Koichi, Yoshida Shuhei. How the scrub height of dwarf pine Pinus pumila decreases at the treeline[J]. Japanese Ecological Research, 2009, 24: 847-854.

[17] Takahashi Koichi. Effects of Climatic Conditions on Shoot Elongation of Alpine Dwarf Pine (Pinus pumila) at Its Upper and Lower Altitudinal Limits in Central Japan[J]. Arctic, antarctic and alpine research, 2003, 35(1): 1-7.

[18] Kajimoto Takuya. Shoot dynamics of Pinus pumila in relation to altitudinal and wind exposure gradients on the Kiso mountain range, central Japan[J]. Tree Physiology, 1993, 13(1): 41-53.

[19] Osada Noriyuki. Crown development in a pioneer tree,Rhus trichocarpa, in relation to the structure and growth of individual branches[J]. New Phytologist, 2006, 172(4): 667–678.

[20] Takahashi Koichi. Shoot growth chronology of alpine dwarf pine(Pinus pumila) in relation to shoot size and climatic conditions: a reassessment[J]. Polar Biosci., 2006, 19: 123-132.

[21] Okuda Masaki, Akihiro Sumida, Ishii Hiroaki,et al.Establishment and growth pattern ofPinus pumilaunder a forest canopy in central Kamchatka[J]. Japanese Ecological Research,2008, 23: 831-840.

[22] Subedi Nirmal, Sharma Mahadev. Climate-diameter growth relationships of black spruce and jack pine trees in boreal Ontario, Canada[J]. Global Change Biology,2013,19(2):505-516.

[23] Gruber A., Wieser G., Oberhuber W. Opinion paper: Effects of simulated soil temperature on stem increment of Pinus cembra at the alpine timberline: a new approach based on root zone roo fing[J]. Eur J Forest Res, 2010, 129:141-144.

[24] Gebrekirstos Aster, Mitlöhner Ralph, Teketay Demel,et al.Climate–growth relationships of the dominant tree species from semi-arid savanna woodland in Ethiopia[J]. Trees , 2008, 22: 631-641.

[25] Rohner Brigitte, Bugmann Harald, Bigler Christof. Estimating the agediameter relationship of oak species in Switzerland using nonlinear mixed-effects models[J]. Eur J Forest Res, 2013, 132: 751-764.

[26] 张连金, 孙长忠, 辛学兵, 等. 北京九龙山不同林分树高与胸径相关生长关系分析[J]. 中南林业科技大学学报, 2014,34(12): 66-70.

[27] Araki Masayuki, Naoki Tani , Araki Masatake,et al.Community structure and growth habit of Siberian dwarf pine (Pinus pumila)[J]. Japanese Journal of Forestry Research, 1993, 75(5): 463-468.

[28] Henry H.A.L., Aarssen L.W. The interpretation of stem diameterheight allometry in trees: biomechanical constraints, neighbour effects, or biased regressions[J]. Ecology Letters,1999,2(2):89-97.

[29] 邓红兵, 郝占庆, 王庆礼, 等. 红松单木高生长模型的研究[J]. 生态学杂志, 1999, 18(3): 19-22.

[30] 马利强, 玉 宝, 王立明, 等. 兴安落叶松天然林单木高生长模型[J]. 南京林业大学学报:自然科学版,2013,37(2):169-172.