创设生活情境，培养数学创新精神

黄志兵

当今世界科学技术日新月异，知识经济初见端倪。知识经济的核心在于创新。数学教育是创新教育的主阵地之一，因此在数学教学中开展创新教育，培养学生的创新能力具有重要意义。本文就新课改下如何在数学教学中培养学生的创新能力谈谈体会。

一、课堂教学中创新能力的培养

1.情境启智 激发创新思维

“兴趣是最好的老师”，当学生对所学的内容产生兴趣时，他们就会不畏艰难，积极主动地进行学习，所以教师应不失时机地给学生创造学习的氛围，结合数学特点，加强问题情境的创设，使学生保持乐思、敢问、勤思的思维状态。例1：在上《有理数的乘方》时，我以“拉面”作为新课的导入，“拉面”是学生最熟悉不过的，它又怎么和数学联系上呢？给这节新课留下悬念，同时，又激发了学生的求知欲，让学生在趣味性的情境中培养学习数学的兴趣，培养学生的探索精神。问题我是这样设计的：你喜欢吃拉面吗？拉面的师傅用一根很粗的面条，把两头捏在一起拉伸，再把两头捏在一起拉伸，再拉伸，反复如此，就把这根粗的面条拉成许多细细的面条。根据上面的情境回答下列问题：

①这样捏合到第4次，可拉出_______根面条。

②这样捏合到第5次，可拉出_______根面条。

你是怎样算出来的？

③有一次拉面的师傅拉出128根面条，请问需要捏合多少次？你是怎样算出来的？

前两个问题同学们根据很快就回答出来，这是为第三个问题铺好“路径”和“台阶”，让学生能够“跳一跳，够得着”，所以第三个问题没过多少时间就得到答案了。有的同学是通过推导得来，有的同学则是通过猜测，其实探索的过程就包含着猜测、错误和尝试，所以同学回答错了，倒是一个好素材。做完了这三题后，又设问如果捏合20次，可以拉出多少根面条？一时无法表达，这样就很顺利地过渡到今天的新课。

2.自主探究 巧设创新机会

新课程注重培养学生独立学习的能力，给他们更多自主探究、独立思考的时间和空间，培养他们创新的思维方式，让学生在学习过程中会如何获得知识的办法，达到培养学生创新意识，提高创新能力的目的。

师：请用线段、等腰三角形、圆通过平移与旋转等变换，设计一个有趣的图案，并用一句简洁的语言说明设计的含义。（同学们也大胆地进行想像，智慧的火花被点燃了。）

3.科学引导 培养创新能力

古人说：“授之以鱼，不如授之以渔。”研究表明，通过小组合作交流讨论的教学方式有利于创新思维的发展。要让学生能运用所学知识，结合自己的生活体验，大胆进行发散创新，就应要求教师善于挖掘教材中的创新因素，通过科学引导，创设情境，使学生在知识网络空间的各个知识点寻找联系，探索解决问题的办法。

例3、在学习变量之间的关系一节时，可以设计这样一个教学过程，来激发学生合作交流的欲望，培养学生的创新能力。

师：通过阅读反映变量之间关系的图象，编写一道符合该图象意义的应用题，并指出横轴、纵轴所表示的意义。

由于问题具有一定的挑战性，独立完成不太容易，于是激起了学生合作学习的欲望，通过合作交流，产生了许多带着自己的经验背景的应用题，而且个别学生还根据图象列出问题。

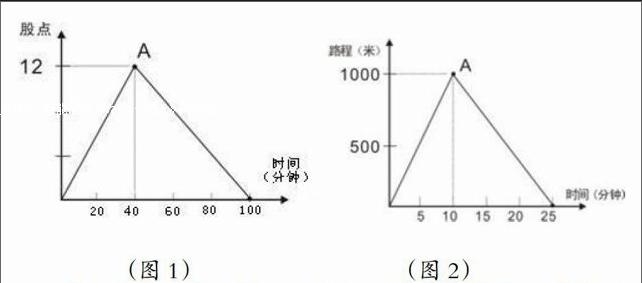
生1：一种股票开盘时呈上升趋势，40分钟上升了12点，以后开始回落，收盘时又回到了开盘时的股点数，开盘60分钟股点大约上升了几点？（如图1）

生2：锅炉工小王用2小时把0℃的冷水烧开了，停火后水温逐渐下降，经3小时又冷却到0℃，问冷却时，每小时水温平均下降了多少度？（如图2）

生3：小明早晨跑步，从家出发1000米后，往回跑，时间与路程的变化如图所示，根据图象回答下列问题：

1.小明何时离家最远？最远距离是多少？

2.什么时候离家500米？

通过老师的科学引导，小组合作交流、讨论，同学们不但拓宽了思路，而且在探究问题的过程中，形成了与他人合作学习的方式，培养学生的创新能力。

4.多种形式 启迪创新思维

教师应从素质教育的角度出发，通过多样化的教学形式，将创新能力的培养渗透到整个教学中去。现代社会信息汇道的多样化，必然导致学生获取知识渠道的多样化。

二、课外学习中创新能力的培养

创新能力的提高非一日之功，课堂学习毕竟只占有限的时间，因此，必须重视课外学习对学生创新能力的培养。由于受应试教育的影响，以往的数学课后教育陷入“题海”中，而忽视了学生培养学生的动手能力，小组合作探究能力。

总之，在数学教学实践中，学生创新能力的培养应贯穿于教学的各个环节，激发学生自主探究的意识，教师要创设适当的问题情境，引领他们以积极的心态去参与鼓励学生发现数学的规律和问题解决的途径，使他们经历知识的形成过程。另外，我们的一切教学活动必须向课外延伸，充分调动学生的主观能动性，引导学生通过动手实践、自主探索与合作交流，只有这样，才能真正地提高学生的创新能力。