基于椭球面模型的鱼眼图像校正方法

杨中伟　杨鸣

摘要： 鱼眼镜头的大视角、短焦距等特点，使鱼眼图像校正算法成为目前图像研究的热点。提出一种椭球面校正模型，通过边缘检测算法获取特征点，运用伪特征点剔除法得到正确的特征点，利用这些真特征点得出校正模型的参数，并以网格图像为例进行研究。实验结果表明，特征点检测准确，得到的模型对网格图像的校正效果好，验证了该校正模型的准确性和有效性。

关键词： 鱼眼镜头； 椭球面模型； 伪特征点剔除； 畸变校正

中图分类号： TP 391.41文献标志码： Adoi： 10.3969/j.issn.10055630.2015.02.008

A fisheye image correction method based on ellipsoid model

YANG Zhongwei， YANG Ming

（College of Information Science and Engineering， Ningbo University， Ningbo 315211， China）

Abstract： Fisheye lens have the characteristics of short focus and wideangle， which makes the fisheye image correction algorithms become hot topics in the field of image research currently. An ellipsoid correction model is put forward. All feature points are obtained by using edge detection algorithm， and the correct feature points are also obtained by using the pseudofeaturepoint elimination method. The correction model parameters are obtained with the correct feature points. The grid image is taken as an example to conduct the research. As a result， the detection of the feature points is accurate and the correction effect is good. It is proved that this model is accurate and efficient.

Keywords： fisheye lens； ellipsoid model； elimination of pseudofeature points； distortion correction

引言在大范围监控、智能交通等领域，为了获得大视角，鱼眼镜头[1]被广泛使用。但是，在获得大范围拍摄视角的同时，为解决在一定的成像面内容纳大视场中的目标物体等问题，鱼眼镜头中不可避免地引入了径向畸变[2]。 如何把存在畸变的鱼眼图像校正为适合人眼观看的图像，显得尤为重要。目前，鱼眼校正算法有高次多项式拟合校正法[3]、球面坐标定位法[4]、球面透视投影约束法[56]、抛物面投影校正[78]、基于渐变方程和经纬映射模型校正[9]及基于几何性质[1011]等方法。现有的方法中，仍存在一些问题：校正公式复杂，校正后图像中有桶形或枕形畸变，校正模型参数拟合需要人工采样。基于这些情况，本文提出一种椭球面校正模型，并且通过自动检测特征点得出校正模型的参数。图1鱼眼镜头成像模型

Fig.1Imaging model of fisheye lens1鱼眼镜头成像模型本文采用椭球面成像模型，成像原理如图1所示。假设相机在场景坐标系的原点O，沿着z轴正方向拍摄，从空间任一点P1（x，y，z）指向原点O的射线，与成像模型曲面交于一点P2，根据正交投影规则过P2做z轴的平行线，交xy平面于点P3（u，v），P3就是空间点P1（x，y，z）经过鱼眼变换后的图像点。鱼眼图像轮廓中心点坐标为（u0，v0），因此空间点与鱼眼图像点之间的关系可表示为（u-u0，v-v0）=M（x，y，z）（1）式中M为本文的成像模型。光学仪器第37卷

第2期杨中伟，等：基于椭球面模型的鱼眼图像校正方法

2鱼眼校正模型拟合

2.1校正模型的建立由椭球面成像模型可知，本文的椭球面校正模型方程为（Ax2+By2）+Cz2+Dz+E=0（2）鱼眼图像在xy平面内是圆心在成像坐标系原点的圆形轮廓，因此，A=B。

2.2鱼眼轮廓的提取及圆心确定现有的鱼眼图像轮廓提取方法中：统计法[12]，当鱼眼图像圆形轮廓区域内存在大量黑色像素点时，该算法失效；扫描线逼近法[13]，设定一个行列极限亮度差的阈值，通过阈值判定是否扫描到鱼眼图像圆形轮廓的上、下、左和右边缘的切线，这4条切线确定了圆形轮廓的外切正方形，据此可得出圆心坐标和半径，但是当鱼眼轮廓不是一个完整的圆形时，该算法与切线法[14]同样失效。本文采用标准圆标定法获取鱼眼图像的圆心和半径，具体做法：预先设定圆心坐标（x0，y0），半径为r0，鱼眼图像中出现一个预置的标准圆形轮廓，通过鼠标拖动，从而调整标准圆的大小和位置，使得标准圆最终与鱼眼轮廓吻合。鱼眼图像的圆心（x，y）和半径r分别为x=x0+Δx（3）

y=y0+Δy（4）

r=r0+Δr（5）式中：Δx为圆心横坐标改变量；Δy为圆心纵坐标改变量；Δr为半径的改变量。

2.3自动选取特征点

2.3.1特征点检测在RGB图像中，令c（x，y）为RGB彩色空间中点（x，y）处的像素值，可表示为c（x，y）=R（x，y）

G（x，y）

B（x，y）（6）令gxx，gyy和gxy分别为gxx=Rx2+Gx2+Bx2（7）

gyy=Ry2+Gy2+By2（8）

gxy=RxRy+GxGy+BxBy（9）其中：在式（7）、（8）、（9）中用符号R、G、B代替R（x，y）、G（x，y）、B（x，y），而R（x，y）、G（x，y）和B（x，y）分别表示在RGB图像上点（x，y）处的R、G、B分量的值； gxx，gyy和gxy均是x和y的函数。函数c（x，y）的最大变化率的方向由角度θ（x，y）给出，变化率的值由Fθ（x，y）给出，其中θ（x，y）=12arctan2gxy（gxx-gxy）（10）

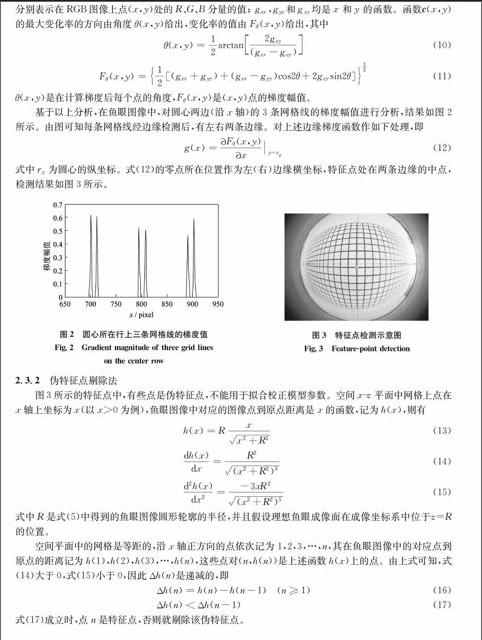
Fθ（x，y）=12（gxx+gyy）+（gxx-gyy）cos2θ+2gxysin2θ12（11）θ（x，y）是在计算梯度后每个点的角度，Fθ（x，y）是（x，y）点的梯度幅值。基于以上分析，在鱼眼图像中，对圆心两边（沿x轴）的3条网格线的梯度幅值进行分析，结果如图2所示。由图可知每条网格线经边缘检测后，有左右两条边缘。对上述边缘梯度函数作如下处理，即g（x）=Fθ（x，y）xy=ry（12）式中ry为圆心的纵坐标。式（12）的零点所在位置作为左（右）边缘横坐标，特征点处在两条边缘的中点，检测结果如图3所示。

图2圆心所在行上三条网格线的梯度值

Fig.2Gradient magnitude of three grid lines

on the center row

图3特征点检测示意图

Fig.3Featurepoint detection

2.3.2伪特征点剔除法图3所示的特征点中，有些点是伪特征点，不能用于拟合校正模型参数。空间xz平面中网格上点在x轴上坐标为x（以x>0为例），鱼眼图像中对应的图像点到原点距离是x的函数，记为h（x），则有h（x）=Rxx2+R2（13）

dh（x）dx=R2（x2+R2）3（14）

d2h（x）dx2=-3xR2（x2+R2）5（15）式中R是式（5）中得到的鱼眼图像圆形轮廓的半径，并且假设理想鱼眼成像面在成像坐标系中位于z=R的位置。空间平面中的网格是等距的，沿x轴正方向的点依次记为1，2，3，…，n，其在鱼眼图像中的对应点到原点的距离记为h（1），h（2），h（3），…，h（n），这些点对（n，h（n））是上述函数h（x）上的点。由上式可知，式（14）大于0，式（15）小于0，因此Δh（n）是递减的，即Δh（n）=h（n）-h（n-1）（n≥1）（16）

Δh（n）<Δh（n-1）（17）式（17）成立时，点n是特征点，否则就剔除该伪特征点。图4特征点及拟合曲线示意图

Fig.4Feature points and the fitting curve

2.4参数拟合式（5）中得到的鱼眼轮廓半径为R，把R代入式（2），则椭球面校正模型的方程简化为（x2+y2）+Cz2+Dz-R2=0（18）代入特征点坐标，得出C=0.707 7，D=189.967 7。上述得到的真特征点及式（18）对应的曲线如图4所示。由图可知，本文提出的校正模型曲线与特征点轨迹相吻合，椭球面校正模型与实际的鱼眼成像曲面接近。由校正模型可得，鱼眼图像点与空间点的坐标关系为u-u0=-DZ+D2Z2+4R2（X2+Y2+CZ2）2（X2+Y2+CZ2）X（19）

v-v0=-DZ+D2Z2+4R2（X2+Y2+CZ2）2（X2+Y2+CZ2）Y（20）式中：（u，v）为鱼眼图像中点的坐标；（u0，v0）为鱼眼轮廓中心点的坐标；（X，Y，Z）为目标校正平面上点的坐标。3实验结果以网格图像为例，运用上述校正模型对鱼眼图像进行校正，结果如图5所示，并与球面校正模型、抛物面校正模型和高次多项式校正模型的效果进行对比，其他校正结果分别如图6、图7和图8所示。

图5本文方法校正结果

Fig.5The correction result by using

the method proposed in this paper图6球面模型校正结果

Fig.6The correction result by using

the spherical model

图7抛物面模型校正结果

Fig.7The correction result by using

the parabolic model图8高次多项式模型校正结果

Fig.8The correction result by using

the highdegree polynomial model

由校正结果可知：球面校正后仍存在桶形畸变；抛物面模型中存在枕形畸变；高次多项式模型校正后图片的中心存在枕形畸变，而在靠近边缘的地方存在桶形畸变；本文的校正模型中不存在畸变，校正效果好。4结语本文依据鱼眼镜头的成像特点，并针对现有算法中存在的不足，提出一种椭球面校正模型，该模型与鱼眼镜头实际的成像模型吻合较好，并用双线性插值法[15]填充像素。实验结果表明，该校正模型取得了比较好的校正效果。参考文献：

[1]肖潇，杨国光.全景成像技术的现状和进展[J].光学仪器，2007，29（4）：8489.

[2]李洪海，王敬东.摄像机标定技术研究[J].光学仪器，2007，29（4）：712.

[3]张景国，将大钢，李晓峰.广角镜头桶形畸变的二元二次多项式修正法[J].光学技术，2010，36（4）：500504.

[4]张宁，刘天键.鱼眼图像校正算法研究与实现[J].闽江学院学报，2012，33（5）：7476.

[5]崔汉国，陈军，王大宇.鱼眼图像校正及拼接的研究与实现[J].计算机工程，2007，33（10）：190192.

[6]DEVERNAY F，FAUGERAS O.Straight lines have to be straight：automatic calibration and removal of distortion from scenes of structured environments[J].Machine Vision and Applications，2001，13（1）：1424.

[7]温灿红，杨强，罗飞，等.一种基于椭圆抛物面透视投影约束的鱼眼镜头校正方法[J].大学数学，2010，26（3）：192195.

[8]周飚，赵鑫，齐志宏，等.一种通用的基于抛物面模型的鱼眼图像校正算法[J].长春理工大学学报：自然科学版，2014，37（2）：2225.

[9]王依桌，席志红.基于渐变方程的鱼眼图像校正方法[J].电子科技，2013，26（10）：7072.

[10]杨晶晶，陈更生，尹文波.一种基于几何性质的鱼眼图像校正算法[J].计算机工程，2012，38（3）：203205.

[11]李根，费章君，杨仕友.基于几何成像模型的鱼眼镜头图像校正算法和技术研究[J].机电工程，2013，30（10）：12681272.

[12]唐俊，赵为民，谷峰.基于鱼眼图像的全景漫游模型[J].微机发展，2003，13（2）：6970.

[13]韩迎辉.基于改进扫描线逼近的鱼眼图轮廓提取算法的研究[J].电子器件，2013，36（6），784788.

[14]常丹华，赵丹，杨峰明，等.提取鱼眼图像轮廓的算法改进及图像校正[J].激光与红外，2012，42（4）：448451.

[15]吴桂萍，吴巍，王成，等.基于双线性插值的鱼眼图像校正方法[J].计算机应用与软件，2012，29（2）：122125.

（编辑：刘铁英）