基于光学扫描法的导轨直线度测量方法
房传明+陈长军
摘要: 基于多测头光学扫描法对导轨直线度的在位测量方法,提出一种新的倾角补偿的三测头扫描方法。介绍了测量原理,推导了基于最小二乘法的直线度形状重构方法,重构出的形状可精确反映直线度误差的高频成分,且对测量噪声有良好抑制能力。对算法进行了仿真验证,并由实验验证了提出方法的有效性。实验结果表明,该方法可以精确地还原出台阶状的直线度形状,测量标准偏差在10 μm以内。
关键词: 扫描测量; 直线度; 三测头法; 倾角补偿
中图分类号: TH 711文献标志码: Adoi: 10.3969/j.issn.10055630.2015.02.001
Straightness measurement of guide rail based on
optical scanning method
FANG Chuanming, CHEN Changjun
(School of Mechanical and Electric Engineering, Soochow University, Suzhou 215006, China)
Abstract: An online measurement method of straightness is studied based on multiprobe optical scanning method. A threeprobe scanning method with tilt compensation is proposed. Reconstructed form can accurately express the high frequency elements of the straightness error, and owns better suppression capability of the measurement noise. The measurement principle of the proposed method is introduced firstly. The construction algorithm of the straightness errors is deduced based on the least square solution and the computer simulation is performed. The experimental system is built for verificating the validity of the proposed method. The experimental results show that the proposed method can accurately reconstruct the straightness errors of step form, and the standard deviation is less than 10 micrometer.
Keywords: scanning measurement; straightness; threeprobe method; tilt compensation
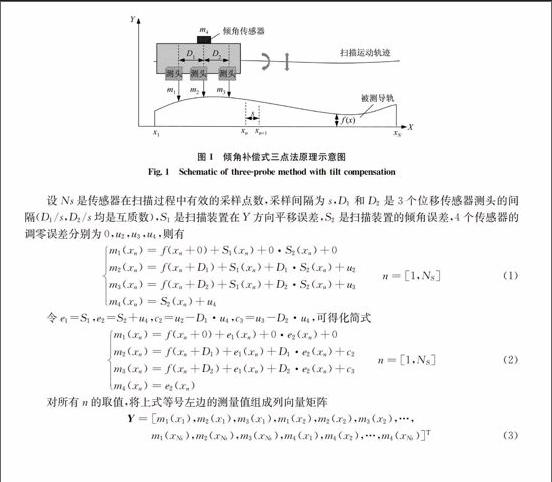
引言直线度误差是导轨加工件的主要形位误差。对于运动平台导轨,直线度误差直接影响着机床、测量机的精度、稳定性和寿命等[13]。为了测量导轨表面轮廓的直线度,常常采用扫描探头法[4]。根据采用位移传感器数量的不同,测量导轨直线度的探头扫描方法有单点法[4]、二点法[56]、三点法[78]等。单点法是最简单的探头扫描方法,只需要1个位移传感器,但这个方法要求扫描装置的运动误差具有良好的绝对精度和重复性。二点法是最简单的多探头扫描方法,它是利用2个位移传感器的输出值的差分来消除扫描装置平移运动误差的影响。目前,研究的二点法主要有Tanaka等提出的连续二点法[5],Kiyono等提出的广义二点法[9],但二点法仍受到测量装置倾斜误差的影响。三点法是利用3个位移传感器来测量直线度,利用3个探头能够消除扫描装置的平移误差与倾斜误差,对探头的差分输出进行双积分后可以计算出导轨直线度。目前,研究的三点法主要有连续三点法[7]、广义三点法[8]等。但是三点法没有考虑各个传感器测头之间存在的调零误差,特别当测量导轨的长度比较长时,此误差所造成的影响就不可忽略[10]。本文提出一种倾角补偿式三点法的光学扫描方法实现对导轨的直线度测量。通过构建数学模型,将调零误差也作为一个计算参数,推导基于最小二乘原理的直线度形状重构方法,并利用MATLAB软件对算法进行仿真验证。搭建导轨直线度自动检测实验平台,实现位移传感器和倾角传感器测量数据的自动采集、自动读取与分析处理,最终完成导轨直线度的测量。1倾角补偿式三点法原理图1为1个带倾角传感器的三测头扫描测量系统,该系统包含1个位移传感器测头单元(3个测头分别为m1,m2,m3)和1个倾角传感器m4。测头单元随着扫描装置沿着X方向移动,实现位移传感器对被测导轨f(x)的扫描,同时,倾角传感器实时采集扫描装置在移动过程中的倾角变化。
图1倾角补偿式三点法原理示意图
Fig.1Schematic of threeprobe method with tilt compensation
设Ns是传感器在扫描过程中有效的采样点数,采样间隔为s,D1和D2是3个位移传感器测头的间隔(D1/s,D2/s均是互质数),S1是扫描装置在Y方向平移误差,S2是扫描装置的倾角误差,4个传感器的调零误差分别为0,u2,u3,u4,则有m1(xn)=f(xn+0)+S1(xn)+0·S2(xn)+0
m2(xn)=f(xn+D1)+S1(xn)+D1·S2(xn)+u2
m3(xn)=f(xn+D2)+S1(xn)+D2·S2(xn)+u3
m4(xn)=S2(xn)+u4 n=[1,NS](1)光学仪器第37卷
第2期房传明,等:基于光学扫描法的导轨直线度测量方法
令e1=S1,e2=S2+u4,c2=u2-D1·u4,c3=u3-D2·u4,可得化简式m1(xn)=f(xn+0)+e1(xn)+0·e2(xn)+0
m2(xn)=f(xn+D1)+e1(xn)+D1·e2(xn)+c2
m3(xn)=f(xn+D2)+e1(xn)+D2·e2(xn)+c3
m4(xn)=e2(xn)n=[1,NS](2)对所有n的取值,将上式等号左边的测量值组成列向量矩阵Y=[m1(x1),m2(x1),m3(x1),m1(x2),m2(x2),m3(x2),…,
m1(xNs),m2(xNs),m3(xNs),m4(x1),m4(x2),…,m4(xNs)]T(3)再将式(2)等号右边的未知量组成列向量矩阵
X=[f(x1),f(x2),…,f(xNs-2),e1(x1),e1(x2),…,e1(xNs),e2(x1),e2(x2),…,e2(xNs),c2,c3]T(4)
至此可得到式(2)的矩阵表达式为Y=AX(5)式中矩阵A为系数传递矩阵,由式(2)等号右边的未知量的系数组成,皆为常量。式(5)的最小二乘解为X^=(ATA)-1ATY(6)求解式(6),即可得到直线度形状f(x)上各点的值。2倾角补偿式三点法仿真验证仿真实验中对不同种类的测试曲线进行了验证,下面仅以阶跃突变曲线为例,说明仿真验证的结果。仿真中采样点数和采样间隔分别为Ns=200和s=1 mm,位移传感器间隔分别为5 mm和6 mm。模拟的阶跃突变曲线函数表达式为f(xn)=20,n=[50,55]
25,n=100
30,n=[130,150]
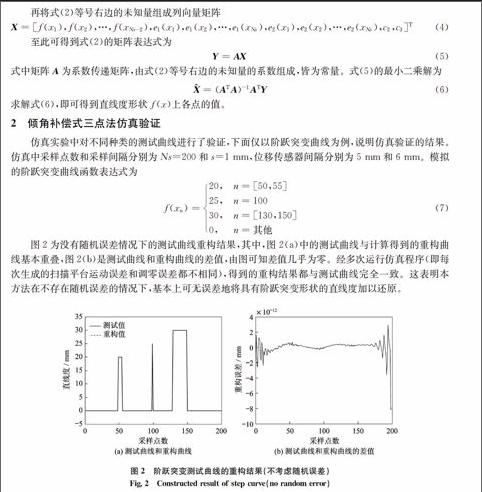
0,n=其他(7)图2为没有随机误差情况下的测试曲线重构结果,其中,图2(a)中的测试曲线与计算得到的重构曲线基本重叠,图2(b)是测试曲线和重构曲线的差值,由图可知差值几乎为零。经多次运行仿真程序(即每次生成的扫描平台运动误差和调零误差都不相同),得到的重构结果都与测试曲线完全一致。这表明本方法在不存在随机误差的情况下,基本上可无误差地将具有阶跃突变形状的直线度加以还原。
图2阶跃突变测试曲线的重构结果(不考虑随机误差)
Fig.2Constructed result of step curve(no random error)
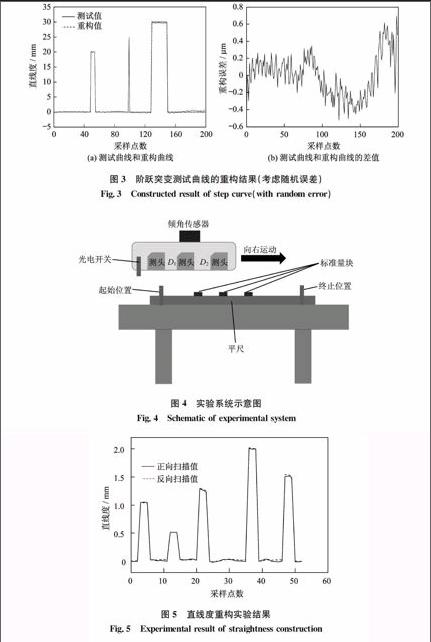
图3为有随机误差的测试曲线重构结果。加入的位移传感器的随机误差的标准差为0.1 μm,倾角传感器的随机误差的标准差每毫米为0.02 μm。由于随机误差的存在,经本方法计算得到的直线度重构结果必然与测试曲线不同。图3(b)是上述测试曲线和重构曲线的差值,由图可知差值的范围大致在±0.4 μm。按照3σ准则,这一偏差范围与输入的传感器随机误差的大小是吻合的。3倾角补偿式三点法实验验证为了对重构结果进行可量化的评价,设计了在一根平尺的表面放置若干不同高度的标准量块的实验方案。安装在扫描平台上的3个位移传感器的测头间隔分别为D1=100 mm,D2=130 mm,扫描平台上水平安装1个倾角传感器,采样间隔为10 mm。此外,为了精确指定测量起始点和终止点,在平尺的相应位置放置标记点,同时在扫描平台上安装光电触发开关,图4为实验系统的示意图。在本实验中,位移传感器的数据是通过位移传感器的配套专用数据采集器进行采集、储存和传输,而倾角传感器和光电开关的数据信号则通过一个数据采集器(研华USB4716)进行采集,所有的数据最后都通过USB接口输入工控机进行自动计算和处理。
图3阶跃突变测试曲线的重构结果(考虑随机误差)
Fig.3Constructed result of step curve(with random error)
图4实验系统示意图
Fig.4Schematic of experimental system
图5直线度重构实验结果
Fig.5Experimental result of straightness construction本实验的实施步骤如下:首先在平尺的中间位置按等间隔放置5块不同高度的量块;接着启动数据采集程序,进入“开始测量”状态;然后启动扫描驱动机构,使扫描平台从平尺的一端运动到另一端;数据采集程序以光电开关监测到的起点和终点为实际的评价点,自动将位移和倾角数据采集并保存;重复前述步骤多次,以取得多组数据;最后对采集到的数据进行分析计算,将包含标准量块的平尺的形状重构出来。图5是本实验的重构结果,包括了正向扫描值和反向扫描值。由图可以清楚地看到5个量块的高度分别为1.0 mm、0.5 mm、1.2 mm、2.0 mm、1.5 mm,而重复性实验得到的标准偏差在10 μm内。4结论本文针对现有直线度测量存在的测量长度受限、精度不高的现状,提出了一种加入倾角传感器的三点扫描实现导轨直线度测量的方法。说明了该方法的测量原理,推导了基于最小二乘法的直线度形状重构方法,根据有无测量噪声等情况对所提出算法进行了仿真验证。仿真结果表明:在没有随机误差的情况下,本方法可无误差地将阶跃突变形状加以还原;在有随机误差的情况下,本方法也具有良好的误差抑制能力。通过一种对叠加标准量块的平尺进行测量的实验,验证了提出方法的有效性。实验结果表明,所提出方法可以精确地还原出台阶状的标准量块,且测量标准偏差在10 μm以内。参考文献:
[1]宁延平,刘战锋.国内外高精度直线度测量技术的研究现状[J].现代制造工程,2005,30(6):8284.
[2]柳常清,宋庆,孙占文,等.双PSD实现长直导轨四自由度测量的新方法[J].光学仪器,2013,35(6):2630.
[3]胡长德,陆加海,幸褀,等.基于激光干涉的长导轨直线度误差测量[J].光学仪器,2008,30(6):1015.
[4]EVANS C J,HOCKEN R J,ESTLER W T.Selfcalibration reversal,redundancy,error separation and‘absolute testing[J].CIRP AnnalsManufacturing Technology,1996,45(2):617634.
[5]TANAKA H,TOZAWA K,SATO H,et al.Application of a new straightness measurement method to large machine tool[J].CIRP AnnalsManufacturing Technology,1981,30(1):455459.
[6]张镭,张玉.时域二点法和三点法直线度EST的误差分析[J].仪器仪表学报,1998,19(1):106108.
[7]GAO W.Selfzeroadjustment of probes in the methods constructing software datum for large profile measurement[J].International Journal of JSPE,1996,30(4):337342.
[8]FUJIMOTO I,NISHIMURA K,PYOUN Y S.Autonomous calibration method of the zerodifference without using a standard gauge for a straightnessmeasuring machine[J].Precision Engineering,2010,35(1):153163.
[9]KIYONO S,GAO W.Profile measurement of machined surface with a new diferential method[J].Precision Engineering,1994,16(3):212218.
[10]GAO W,YOKOYAMA J,KOJIMA H,et al.Precision measurement of cylinder straightness using a scanning multiprobe system[J].Precision Engineering,2002,26(3):279288.
(编辑:刘铁英)