风电机组叶片钝尾缘翼型改型方式的研究
文 | 李磊,王旭玲
风电机组叶片钝尾缘翼型改型方式的研究
文 | 李磊,王旭玲
柔性叶片应用于风电越来越广泛,叶片最大弦长处的变形与载荷随叶片长度的增加也逐级增加,为了改善最大弦长处叶片外形变化的特殊性,减小结构设计的难度,在该位置应用厚尾缘翼型,成了一个性价比较高的选择。它不仅能够增加叶片的截面面积和惯性矩,而且在气动方面也凸显了更多优势。一个设计优秀的厚尾缘翼型,不仅能够提高最大升力系数和升阻比,其良好的失速性能也让长时间处于失速区的最大弦长位置得到良好的运行,它可以降低气流通过截面最厚点的逆压力梯度,从而推迟或者避免气流的分离,并能够在后缘的后端形成一个由边界层形成的自适应尖后缘,使气流一直附着在翼型表面,改善气动性能,从而后缘加厚的改型方式成为风力发电机组翼型的发展趋势。
该文针对荷兰DELFT大学开发的DU40翼型进行一些改型的探索,后缘厚度增大为原始翼型的两倍,以求获得较好的气动性能和良好的结构抗载能力。该文针对DU40翼型进行了4种不同的改型,包括改变厚度分布曲线、刚性旋转翼型的上下弧线、在翼型中弧线两侧对称增加厚度和直接进行尾缘的切割方式。在四种不同的改型过程中,计算了上百个不同的新翼型,并使用Xfoil软件对该系列翼型的气动性能进行计算,从中得到性能优良并对结构特性有较大帮助的翼型。该文针对不同改型方式进行了对比,得出一个好的钝尾缘翼型的改型方法,使用指数函数改型过程中对指数幂分别等于1、2、3、4、5的翼型性能进行了计算,从而得到一个较好的幂的取值,减少在未来改型过程中的工作量。
使用Xfoil软件的理论验证
Xfoil是一个为设计和分析亚音速飞机独立翼型编写的互动式程序。它对一种已经存在的翼型进行粘流或者无粘流分析,允许强制或者自由转换、转戾的气泡分析、卡门压缩性修正。它除了计算最大升力系数,还可对升力和阻力进行预测。Xfoil对于钝后缘的处理方法,可参考Drela发表的《对钝后缘的完整边界层公式》。
叶片最大弦长处雷诺数约在2E6—6E6之间,对于大部分的运行时间所处的雷诺数为4E6,所以该文选取雷诺数为4E6,通过对DU40翼型计算的升阻力系数与实际测试的升阻力系数进行对比,其失速攻角预测较为准确,失速之前,升阻系数最大误差为±10%,其中,Xfoil对于升力系数的预估较高,对于阻力系数的预估较低。升阻比对叶片整体的气动效率有较大作用,所以将升阻比作为该文主要参考目标,另外,其升力系数和阻力系数的大小对于气动载荷也有一定的影响。
改变厚度分布曲线
一、改变厚度曲线方式
改变厚度曲线方式是通过指数函数进行吸力面和压力面的翼型改良,这种改良方式能够在较窄的翼型范围内光顺地将原始翼型修改到所需翼型,并且可以对指数幂进行人工选择,从而得到多种新翼型。改变厚度分布曲线可用方程
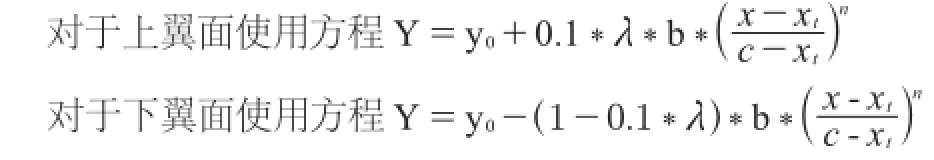
其中:n=1、2、3、4、5,b表示尾缘增加的厚度,C表示弦长,xt表示厚度改变的起始位置,λ表示上翼面占改变厚度的百分比。针对改变厚度的分布曲线,xt分别为最大厚度(弦线30%位置)、弦线60%、弦线80%三个位置进行改变后缘厚度为原来的两倍,λ为10、8、2、0。我们采用上述方程进行DU40翼型的改型,再计算其气动性能进而从中选择优秀的新翼型。
二、计算结果的对比
经过计算,得到如下结果,(1)当λ=0、2、8、10,xt=0.3时,升阻比对于原翼型均有所增加,且当n=5时,升阻比较好,随着n值的下降,升阻比曲线也开始变缓,最大升阻比依次下降。(2)当λ=0、2,xt=0.6、0.8,且n=5时,升阻比较好,此时有最大升阻比,随着n值的下降,升阻比曲线也开始变缓,最大升阻比依次下降。(3)当λ=8、10时,xt=0.6、0.8时,且当n=1时,升阻比较好,最大升阻比相差较小,在大攻角区域升阻比较高。
三、性能良好翼型的比较
经过计算,选择性能良好的三个新翼型和原始翼型的升阻比进行比较,当λ=10时,翼型在高的攻角会产生较大升阻比,提高翼型性能,翼型修改在吸力面后缘方向可以使翼型失速性能也有较大的提高。从中选取三种修型且升阻比曲线优秀的进行比较,分别为xt=0.3,n=5;xt=0.6,n=1;xt=0.8,n=1。从图1看,当叶片在弦线0.6*C的位置,进行吸力面后缘直线增厚可以获得最优升阻比。最大升阻比有较大提高,在失速区域也可以产生较好的升阻特性。对于叶片功率的提高有积极的影响。
刚性旋转上下翼型的两条弧线
刚性旋转翼型的两条弧线,翼型的吸力面和压力面的曲线分布都经过改变,包括翼型最大厚度。从图3看,翼型升阻比有较大的提高,在大攻角下也有较好的性能。翼型产生最大升阻比的攻角没有改变。
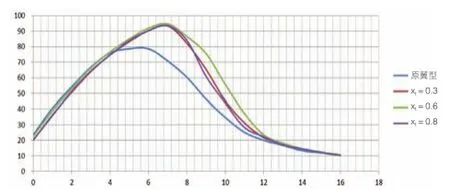
图1 当λ=10,不同xt取值,几个翼型的升阻比对比
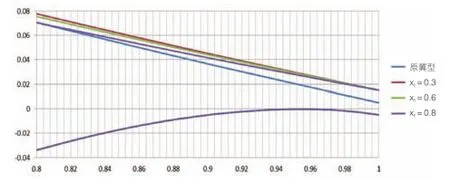
图2 当λ=10,不同xt取值,几个翼型的外形对比
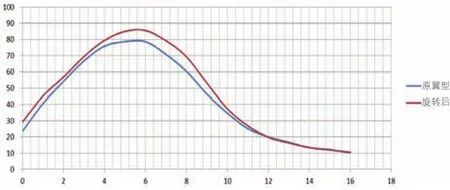
图3 旋转前后翼型升阻比对比
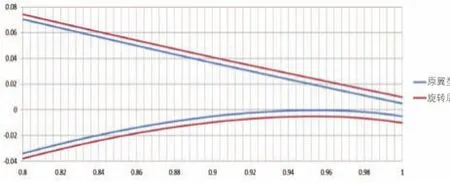
图4 旋转前后翼型翼型变化情况
翼型中弧线两侧对称增加厚度
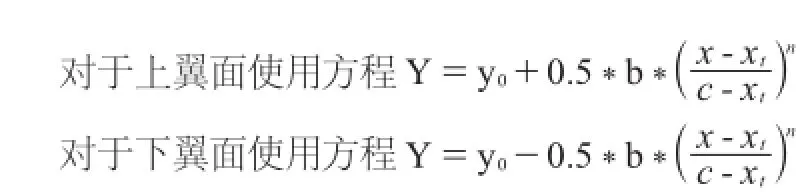
其中:n=1、2、3、4、5,b表示尾缘增加的厚度,C表示弦长,xt表示厚度改变的起始位置。针对改变厚度的分布曲线,xt分别为最大厚度(弦线30%位置),弦线60%,弦线80%三个位置进行改变后缘厚度为原来的2倍。我们采用上述方法进行DU40翼型的改型,再计算其气动性能。
经计算,当xt=0.3时,取n=5;当xt=0.6时,取n=1;当xt=0.8时,取n=1,选取三个优良翼型,从图5看,当xt=0.6会得到较好的升阻比曲线。
直接进行切割
在翼型的0.95*弦长处进行切割,此时后缘厚度为原来的两倍,为了得到标准翼型,再对切割后的翼型按照比例进行弦向方向的放大,这种修型较大的改变了最大厚度的位置,翼型的厚度分布和弯度分布,切割后翼型靠近后缘位置变化较大,叶片弯度变小,使该切面结构力的分布更均匀。从图7看,切割后的翼型升阻比较原始翼型下降较多,但曲线缓和,对于最大弦长位置气动性能要求不高的叶片来说也是可取的,切割后的翼型在大攻角区域相对原始翼型的升阻比曲线好。
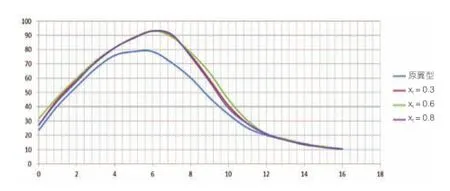
图5 不同xt,三种较好修型的升阻比对比
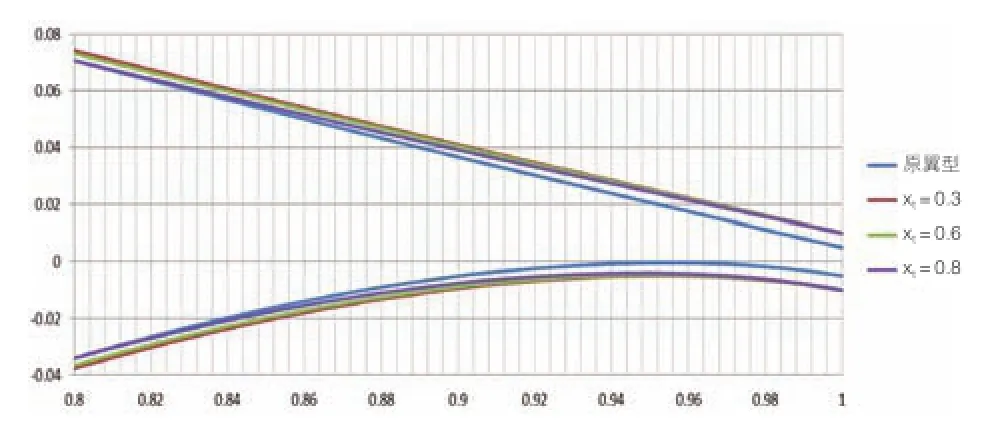
图6 不同xt,三种较好修型的翼型对比
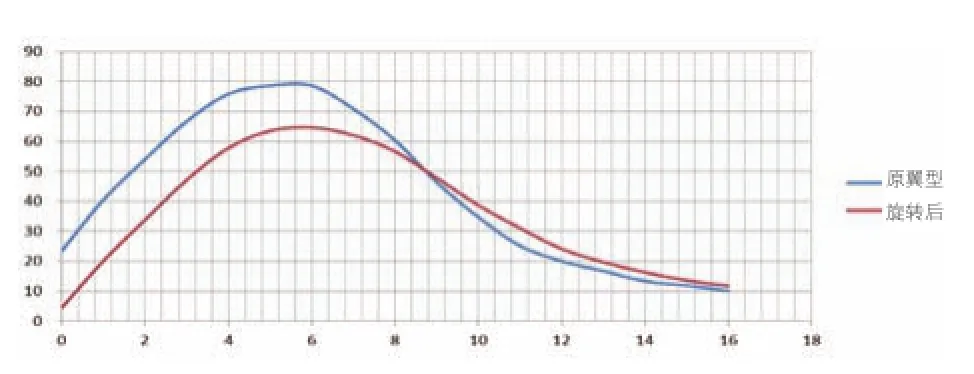
图7 切割前后翼型升阻比的对比
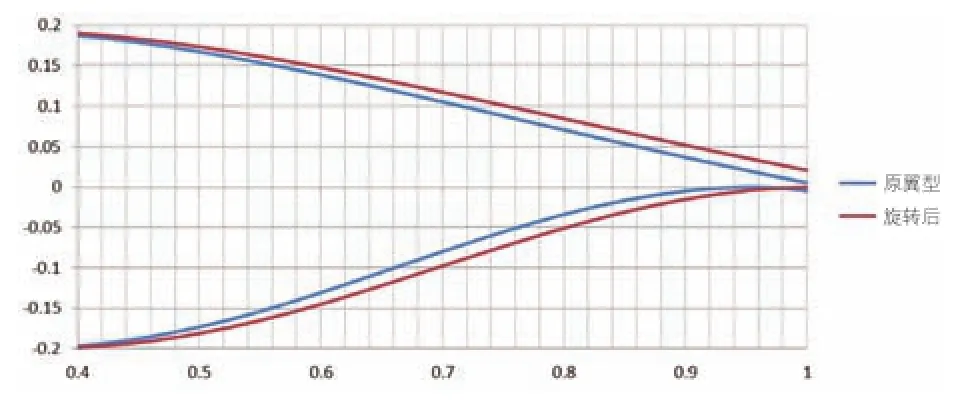
图8 切割前后翼型外形的对比

图9 四种改型的升阻比比较
改型翼型的比较
通过计算,对中弧线对称增加和改变厚度分布曲线两种改型方式均选择一种气动性能优秀的翼型,然后对四种改型方式后的翼型进行比较。可以发现对于翼型的改型方式,改变厚度分布曲线能够得到较好的翼型分布,其中改变厚度分布曲线的时候,对于吸力面进行后缘加厚,不改变压力面的形状可以得到较好的性能,当n=1时能够取得较好的分布形态。
结论
(1)对于改变厚度分布曲线的修型,对翼型的吸力面进行后缘增厚,不改变压力面弧线的形状,这样能够得到较好性能的翼型。当xt=0.6时,修型翼型气动性能最好。当选取指数函数进行修型时,n的取值是随修型的起始位置改变的,一般的当n=5或者n=1时,其修型翼型性能较好。
(2)对于刚性旋转翼型的修型,能够提高翼型的气动性能。
(3)对于中弧线两侧对称增加厚度的修型,一般也能够增加翼型的气动性能。当xt=0.6时,修型翼型气动性能最好。
(4)对于直接进行切割的修型方法会减小修型后翼型的气动性能。这种修型对于翼型最大厚度位置、弯度分布、厚度分布都较大,这样对于一个已经成为优秀的翼型的修型都处于不利的地位。
(作者单位 :中航惠腾风电设备股份有限公司)

