社区健康质量灰评估模型研究

陈 阳，牟 岚，张博文，金新政

（华中科技大学健康信息资源研究中心，湖北 武汉 430074）

· 调查与理论研究 ·

社区健康质量灰评估模型研究

陈 阳，牟 岚，张博文，金新政

（华中科技大学健康信息资源研究中心，湖北 武汉 430074）

在综合考虑社区健康质量特点的基础上，建立了包括5个一级指标、15个二级指标、32个三级指标的评价指标体系，并利用优序图法确定指标权重、双基点灰关联排序法构建评估模型，对后期的相关研究提供方法学支撑和理论基础。

社区；健康质量；指标体系；指标权重；灰评估模型

随着社会经济的发展，人们的生存环境发生了很大的变化，缺乏体育锻炼、使用快餐等不健康的生活方式导致各种急、慢性病发生，日益威胁着人们的健康。健康质量已经成为衡量一个国家政治、经济、文化以及卫生水平的重要标志[1]。社区健康质量与社区的经济文化、居民生活行为、医疗卫生保健条件等因素息息相关[2]。由于社区健康质量评价系统是一个多因素多层次的灰色系统，在该系统中，各评价指标已知，但各指标之间的相互影响属灰色信息，本文采取灰色关联方法对社区健康质量进行评估，建立灰评估模型[3]。

1 社区健康测评指标的建立

1.1 评估指标及初步确立的原则

在建立社区健康质量测评指标体系时，研究小组采用头脑风暴的方法，邀请了各类专家，包括社区研究人员、工作人员、管理人员以及居民代表，使得指标的确立能代表各个相关利益层级人员。

指标体系要具有科学性，每项指标都要经过科学的调研与论证，不仅要得到专家的认同，还要有科学依据，有一定的理论基础；指标体系要具有实用性可行性，要尽量简明扼要，操作性强；还要具有独立性，具有良好的代表性，各项指标间不会相互交叉。

1.2 社区健康质量测评指标体系的修改与确立

由于社区健康质量测评指标所包含的内容复杂，在初步建立社区健康质量测评指标体系后，采用德尔菲法综合领域内权威专家的观点及看法，并对初步建立的指标体系进行检测和筛选，并根据专家意见对指标体系进行修改。

德尔菲法在进行预测分析时，能有效对目标进行系统分析，对未来发展中的各种可能出现的前景做出概率评估[4]。而社区健康质量测评指标体系的建立，与当今社会的具体生活环境、人们日常生活的主观感受密切相关，使用德尔菲定性分析方法能有效使各种主观变量定性化，为社区健康质量测评奠定良好的基础[5]。

德尔菲法具有匿名性、轮间反馈性、预测结果的定量处理等特点，德尔菲法采用函询方式收集专家意见，简便灵活；并且征询的专家都独立思考独立判断，不会相互影响，分析结果具有代表性[6]；由于德尔菲法是轮番多次征询专家意见，每一轮的征询结果都会反馈给各个专家，能有效提高结果的可靠性和全面性。

通过上述研究，研究小组最终建立了包括5个一级指标、15个二级指标、32个三级指标的评价指标体系。

2 社区健康质量评价指标权重的确定方法

本研究采用简单优序图法评价指标权重，优序图的空白格式如图1所示，这是一个棋盘格的图式，共有n×n个空格，n取决于需要比较的对象的数目，此处画5×5=25个空格，供比较5个对象之用，如果比较的对象数目多于或少于5个，那么优序图的行或列的数目多于或少于5个，那么优序图的行或列的数目也要相应增多或减少。图的左面供填写“比较对象”之用，每一对象均分别用顺序代号1～n表示，图示上方也写出1～n的顺序代号，每一代号也表示与图的左方相同的比较对象，但图的左方表示“比较者”，图的上方表示“被比较者”。由于自身比没有意义，所以凡是代表相同顺序号相比的空格均涂为黑色，表示此格已不能填数字，用“1”表示两两对比中相对“大的”、“优的”、“重要的”，而用“0”表示“小的”、“劣的”、“不重要的”。当所有的两两对比都进行完毕并填上对比结果的数字后，这个简单优序图就填满了。接着，在图的右方作合计计算，即把各行所填的各格数字横向相加，把所得总数写在右上方，把每一行的合计进行纵向相加，得到总数[7]。

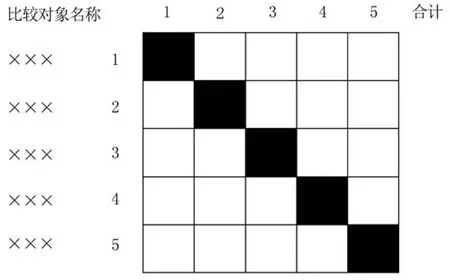
图1 优序图的空白图式

本文用Fi表示表格右方每一行横向相加的合计，则每个指标的对应权重用Wi来表示，n用来表示指标个数，各指标权重可通过如下公式计算得出。

根据上述指标体系以及权重计算方法的研究，得到表1。

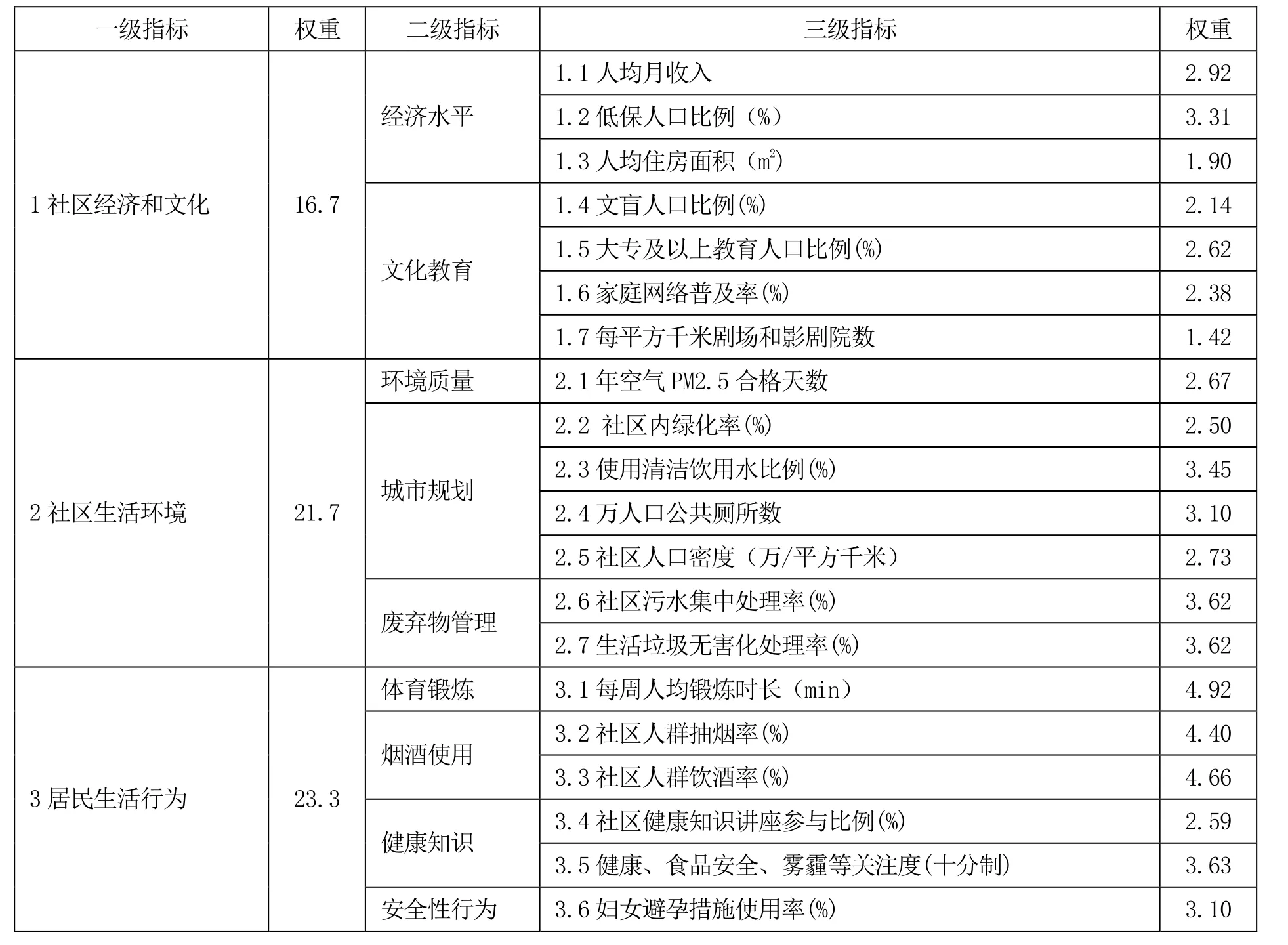
表1 指标体系及其权重

续表1 指标体系及其权重

3 社区健康质量灰评估模型

由于进行社区健康质量测评时指标的选取和数据的采集难度较大，数据统计数量有限，因此，本研究选取灰关联评估模型。该模型对样本量没有很高的要求，并且计算量相对较小，具有使用方便的特点[8]，并利用灰关联分析方法对社区健康质量进行测评和分析。

本文利用基于灰关联的评估方法中的双基点灰关联排序法构建评估模型。多指标综合排序方法是近年来系统分析面临的一个新课题，为此产生了“双基点灰关联排序法”[9]。排序方法及步骤如下：

3.1 确定最优方案和最劣方案

最优(劣)方案的指标是根据排序方案的外界而产生，最优(劣)方案根据需要排序的这类方案的性质、设计(规定和要求)能力，以及各指标在过去曾出现过的最优(劣)值，结合现在已出现和将来可能或希望出现的最优(劣)值而定。因此，最优(劣)方案具有稳定性，能大大简化计算。

扩大了的指标矩阵为：

由于最优最劣方案的确定要根据外界因素产生，因此，在经济社会的不同发展阶段会有不同的最优最劣方案，由于外界因素的发展在一定时期内是稳定的，使得最优最劣方案一旦定下来便在一定时期内保持稳定。

3.2 对指标矩阵标准化

对于指标属性是越大越优的指标用公式2进行标准化：

对于指标属性是越小越优的指标用公式3进行标准化：

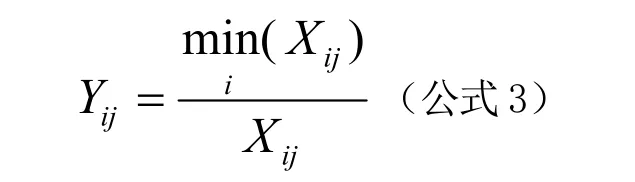
其中：

Xij——是第i个区第j个指标的元素；

Yij——为第i个区第j个指标无量纲化后的数值。

显然，标准化后aˆij的值均为越大越优，且0≤aˆij≤1。因此，标准化指标矩阵为：

对标准化指标矩阵进行加权处理，得到加权标准化指标矩阵：

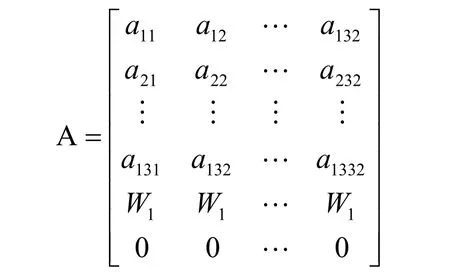
3.3 确定理想点和反理想点

根据以上分析，将矩阵A中的E向量作为理想点，C向量作为反理想点，即：理想点：I+=（i1+, i2+,…，i32+），反理想点：I-=（i1-, i2-,…，i32-）

从A中明显看出：理想点和反理想点就是通过对最优方案和最劣方案进行加权标准化所得到的结果，即I+=E=W；I-=0。而且还应注意到，最优和最劣方案的变化对理想点和反理想点没有影响。换言之I+≡W，I-≡0，使得理想点和反理想点构成的空间成为稳定的排序参照对象。

3.4 计算具体的排序方案与理想点及反理想点之间的灰色关联度γ

设排序方案与理想点的灰色关联度为γ+++，则灰色关联度的计算如公式4[10]：

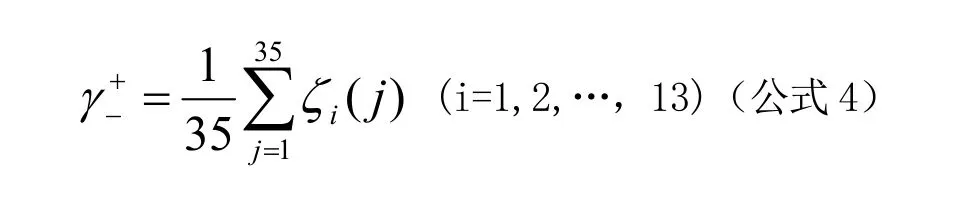
其中，实数ζi(j)为灰关联系数，灰关联系数的计算如公式5：

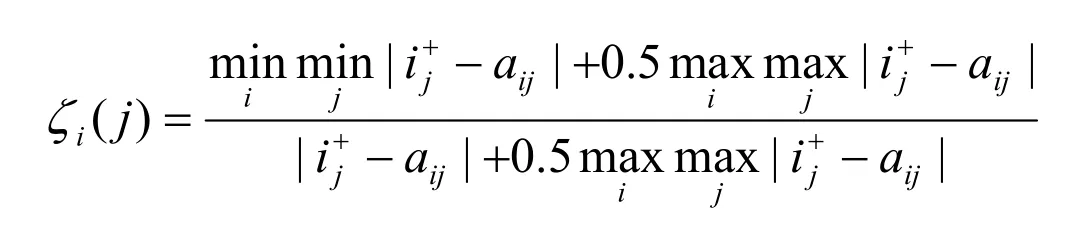
（公式5）

其中，γ+值越大，说明Si与I+越贴近；同理可以计算出Si与反理想点的灰色关联度γ-[11]。

3.5 根据灰色关联度计算各方案的综合排序值Z

根据灰色关联度计算出来的综合排序值以综合Zi值由大到小进行排序。

4 分析与讨论

在复杂的社会环境下，进行社区健康质量测评研究，研究本身会受到外界各类因素的影响，收集的数据也会存在不同程度的偏差，即具有一定的灰色性。利用灰关联分析方法能从抽象的数据中找到关键点，对于科学决策具有有利的影响[12]。

本文构建了基于武汉市13个行政辖区包含32个指标的评估模型。虽然32个指标是已知的，但是各指标直接的影响是灰色的，过程是灰色的，所以本文建立了灰评估模型。灰色理论的依据是信息覆盖，即使用一组信息去包容覆盖既定的命题，用已知的一些定量描述通过灰色生成手段来研究系统性质，最终给出定性分析，找出规律[13]，而灰关联理论是灰色系统中理论最成熟，应用最广泛的部分[14]，基本原理就是通过统计比较以分清系统中多种因素之间的关联度，这样既保护了既有信息也减少了误差[15]，所以本文构建基于灰评估的社区健康质量模型是合理的。此外本研究所建立的灰评估模型具有很强的适用性，能对不同社区的健康质量进行测评，并按照健康质量的高低进行排序，社区还能根据测评的结果对不足的地方进行改进，以提高整体健康质量，因此本研究对于社区健康质量的实证研究具有较强的现实意义。

本研究所建立的评估模型能克服数据收集上的缺陷。该评估模型在数据收集不齐全或没有具体的数据，但需要进行比较分析的情况下适用。通过灰关联评估方法，对数据进行无量纲化处理，可以将数据直接相加，对数据进行综合分析，使得分散的信息能集中化，从而能进一步进行分析比较。

该评估模型应用的范围广泛，能评估健康指标、服务质量、安全质量等。由于该评估模型对样本数量没有要求，也不需要样本量遵循某种统计分布规律，而且计算量小，使用简便，因此能够得到广泛的使用，并为决策提供理论支撑。

[1] 韩 超.社区管理绩效评价体系的构建——基于西宁市城东区社区管理的视角[J].河北经贸大学学报(综合版),2014,14 (2):102-104.

[2] 于 博.高校教师健康状况及社区干预策略研究[D].武汉:华中科技大学,2012.

[3] 邢月梅.社区健康教育对老年人生活质量的影响及评价[J].山东医学高等专科学校学报,2013,35(1):40-42.

[4] 汪 云.区级社区卫生服务系统绩效评价指标体系研究[D].武汉:华中科技大学,2008.

[5] 朱 霖.欠发达地区农村社区卫生服务能力评价指标体系研究[D].南昌:南昌大学,2010.

[6] 张振建,冯占春,黄 锐,等.基于平衡计分卡的护理人员绩效评价指标体系研究[J].医学与社会,2012,25(3):25-27.

[7] 史建平,古丽扎尔•艾海提,李卫星.优序图在确定住院医师规范化培训考核指标体系权重中的应用[J].中国卫生统计,2010,27(4):377-378.

[8] 周秀文.灰色关联度的研究与应用[D].长春:吉林大学,2007.

[9] 唐伟勤.高校教学质量的多指标多层次灰关联评估[J].经济师,2008,(4):25-26.

[10] 张 莎.灰色关联分析新算法研究及其意义[D].长春:东北师范大学,2012.

[11] 刘思峰,蔡 华,杨英杰,等.灰色关联分析模型研究进展[J].系统工程理论与实践,2013,33(8):2041-2046.

[12] 孙玉刚.灰色关联分析及其应用的研究[D].南京:南京航空航天大学,2007.

[13] 曹明霞.灰色关联分析模型及其应用的研究[D].南京:南京航空航天大学,2007.

[14] 张 可.矩阵型灰色关联分析建模技术研究[D].南京:南京航空航天大学,2010.

[15] 袁 园.换流变压器故障风险的灰色关联评估方法[D].重庆:重庆大学,2010.

（本文编辑：张永光）

Study on gray assessment model of community health quality

CHEN Yang, MOU Lan, ZHANG Bo-wen, JIN Xin-zheng
(Health Information Resources Research Center of Huazhong Science and Technology University, Wuhan Hubei 430074, China)

This research studied the community health quality, and in the basis of the comprehensive consideration of community health, we established evaluation indicator system including 5 primary indicators, 15 secondary indexes, 32 tertiary indicators of evaluation index system, and used the method of superiority chart to determine the index weight, this study would provide similar studies with methodological support and theoretical basis.

community, health quality, index system, index weight, grey assessment model

R197.61

B

1003-2800（2015）10-0646-04

2015-06-17

国家科技支撑计划项目（2008BAI52B00）

陈 阳（1990-），女，湖北武汉人，在读硕士研究生，主要从事卫生信息管理、社区健康质量、社区养老服务等方面的研究。

金新政（1958-），男，河南遂平人，硕士，教授，硕导，主要从事软科学、管理学、信息系统方面的研究。