热带法测量导热系数时材料最小厚度的确定
雒彩云, 杨莉萍, 陶 冶, 徐子君, 钟 秋
(中国科学院上海硅酸盐研究所,上海 200050)
0 引言
导热系数是表征材料热物性的重要参数,是衡量材料能否适应具体热过程的依据,是对特定热过程进行分析计算、从事工程设计的基础数据。研究材料的导热系数不仅能为系统热优化提供关键参数,而且能为材料配方和微结构设计提供重要的科学依据,比如电厂的热网管道、石化炼油工程中的裂解炉、建筑外墙保温层的设计中,导热系数是个非常重要的设计参数,同时也是各种热过程温度场模拟的重要计算参数[1-5]。导热系数的准确性直接影响设计及模拟计算的可靠性。目前,测试仍然是获得准确导热系数的唯一途径。
导热系数测试方法按照热流状态来分,主要有稳态法[6-8]与非稳态法。热带法就是属于一种非稳态测试方法,相比稳态法,热线法最大的特点是:测试周期短、对环境要求低、重现性好、准确度高、制样方便,适用于较小导热系数材料的测量。早在20世纪30~60年代热线法就被用来测量液体的导热系数[9-10]。热带法是在热线法基础上发展起来的,与横截面是圆形的热线相比,薄带状的热带与待测样品能更好地热接触,更适合测量固体材料的导热系数。发展到现在,热带法有了更广阔的应用,比如可测复合材料、含湿多孔介质、非透明材料与半透明材料、气体及保温材料常温或者高温导热系数[11-15]。
1 热线法原理及模型
热带法原理如图1所示,在均质匀温的无限长无限大的圆筒状介质中心线处放置一根细长的金属加热丝,以恒定功率加热,加热丝与介质周围的温度会升高。如果被测材料的导热系数高,那么产生的热量将较快传递出去,热线温升较小;相反如果材料导热系数小,产生的热量散发得慢,热线温升的高低快慢与介质材料的热物性参数有关[16]。
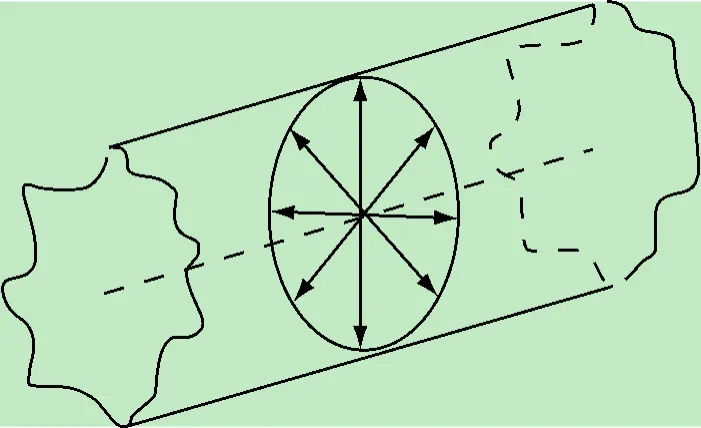
图1 热线法原理模型
热线法温场用一维圆柱坐标描述,选择热线中点位置为测温点,则该点温度随加热时间变化的规律应遵循其导热微分方程。对此方程进行求解,得到导热系数的计算公式:
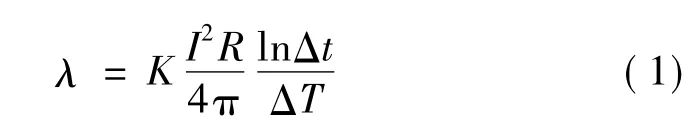
其中:λ为导热系数(W/mK);q为单位长度热线的加热功率(W/m);t1,t2为热线加热的起止时间(s);T1,T2为t1,t2时刻各自对应的温度(℃或者K)。
由公式可见,热线的温升随着时间的对数成线性变化,导热系数可由升温曲线与其所对应的时间对数构成的曲线的近似直线之斜率得知。
2 fluent模拟计算
2.1 物理模型
热带法测试模型如图2所示,相同材料的试样1、2上下放置,中间有一根金属加热带。通过fluent建模,由于加热过程中样品内部温度场是以加热带为轴径向分布,所以选取热带及样品中间一块截面进行分析计算,如图3所示。
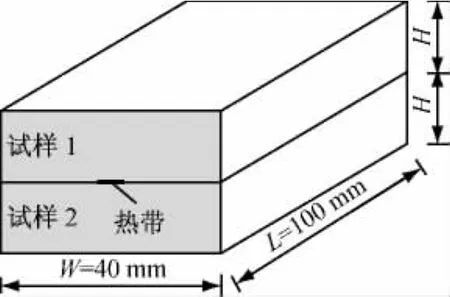
图2 热带法测试模型
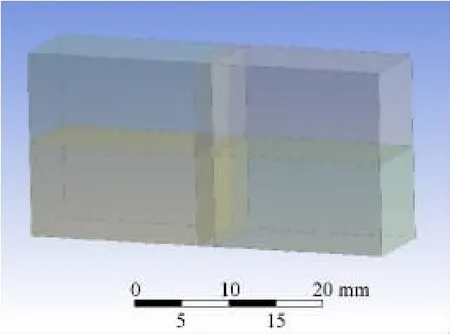
图3 模拟计算截面选取
2.2 控制方程及边界条件
本研究只针对热带法在常温测量时厚度对测量准确性的影响,故不考虑外表面对流散热和辐射散热的因素;只考虑样品与热线之间的热传导,忽略接触热阻,外表面做绝热处理,其控制方程及边界条件如下。
热传导控制方程:

边界条件:外表面热流量h=0;加热丝加热功率q=q(t)。
初始条件:T(x,y,z),t=0。
式中:c为试样的比热容;ρ为试样的密度;Ta为试样的初始温度(选取20℃),q是加热丝加热功率。根据热线法的测试标准GB/T10297-1998,选取了4种不同的导热系数参数,且为了达到理想温升(15~20℃),采取不同导热系数用不同功率加热方法。加热丝及样品的物理计算参数如表1所示。加热功率根据导热系数大小选取:导热系数为 0.1、0.5、1.0、1.5 W/(m·K)时的加热功率分别为 0.484、1.760、3.300、4.640 W。
2.3 模拟计算结果
求得的导热系数计算值相对误差随着材料不同厚度变化的关系如图4所示。由图可以看出,随着材料厚度的减小,计算值持续偏小,且较小导热系数偏小的趋势比较大导热系数的明显缓慢。以相对误差在±5%为界,由图可见,0.1、0.5、1.0、1.5 W/(m·K)对应的最小测量厚度依次分别为4.5、10、13、16 mm,这是由于导热系数越大,热量越容易传播出去,在同样的测量时间内,样品外表面的温度已经发生了变化,不再满足热带法理论模型假定的无限大介质条件,即外表面无温升的要求。选取图2中样品1的上表面中心做为参考点,计算得到该点最大温升随厚度的变化如图5所示,由图看出,同样的厚度,导热系数越大,外表面温升越大,俨然零温升已不满足,因此相对误差也越大,这与图4的计算结果相吻合。
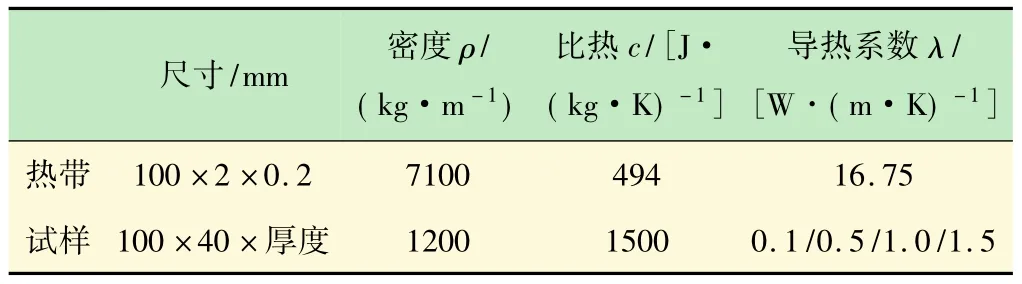
表1 热带及试样物理计算参数
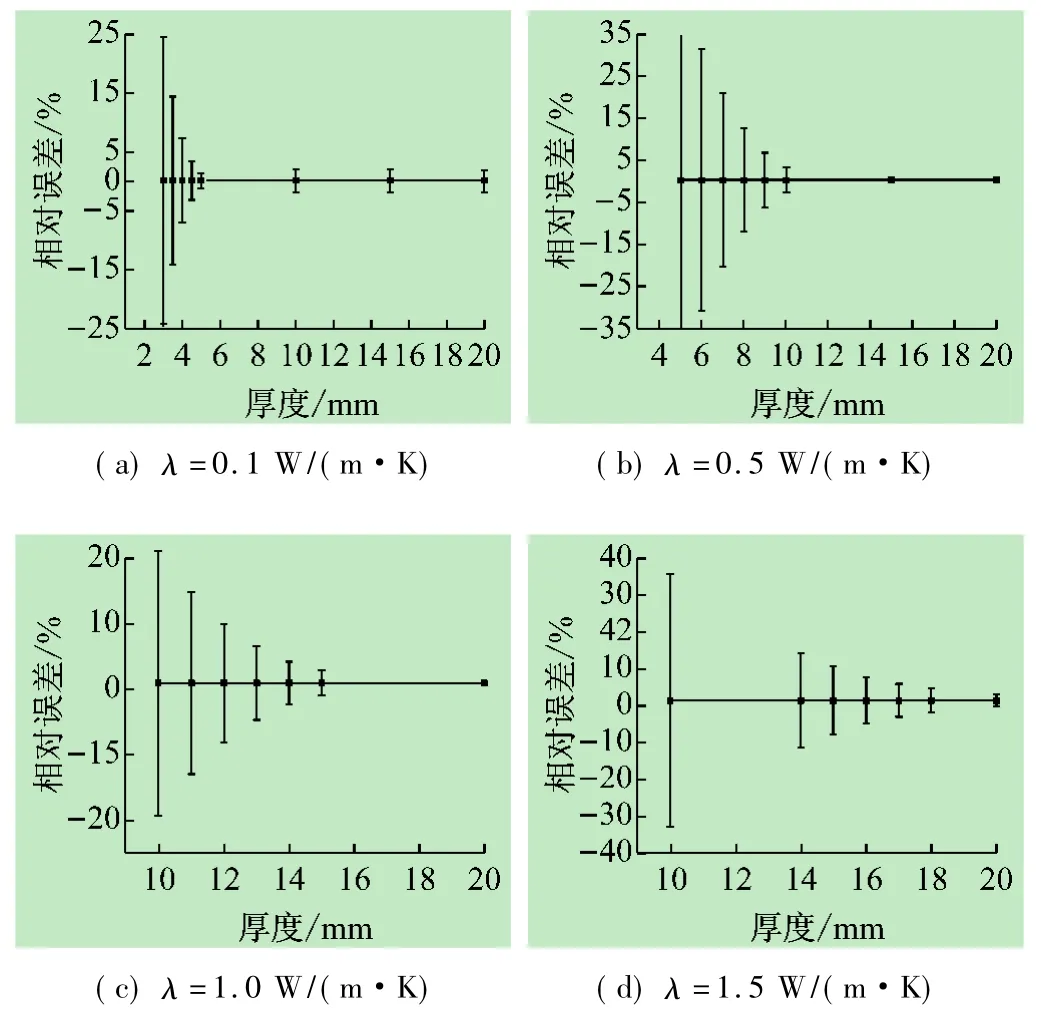
图4 导热系数计算误差随材料厚度的变化
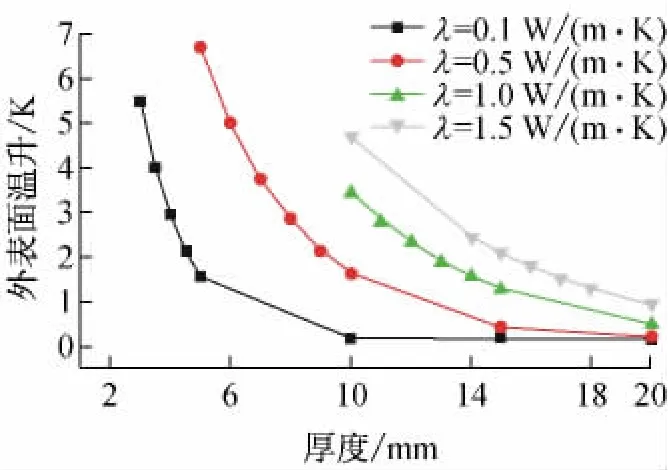
图5 样品外表面最大温升随材料厚度的变化
3 实验验证与结果
整体测试系统如图6所示,硬件部分主要有加热炉及其控制系统、加热丝与恒流电源、热电偶信号放大及其冷端补偿,软件部分包含温升曲线及热电偶信号的采集、A/D转换、信号放大处理等。加热丝采用Cr20Ni80合金,由恒流源提供恒定功率加热,K型热电偶测量热带温升及样品温度,通过毫伏表采集后送到计算机处理显示。

图6 测试系统整体示意图
实验选取3种材料,代表3种不同数量级的导热系数,样品长宽均为100 mm×40 mm,厚度选取依据计算条件,从20 mm左右开始依次递减,测量时间均为100 s,温升控制在10~20℃,以便尽量减少温升因素引起的误差,计算结果如表2所示。由表看出,在合理的温升范围内,材料越厚测量值越接近实际值;随着厚度的减小,测试偏差越来越大,且总体呈现偏小的趋势,这两点与模拟计算结果相一致;测量的最小厚度临界尺寸大于计算的临界尺寸,这是由于计算时忽略样品与热丝之间的接触热阻,而实际测试时由于接触热阻存在,使得测量值偏小幅度更缓慢,从而使得一定允许误差范围所对应的临界尺寸变大。
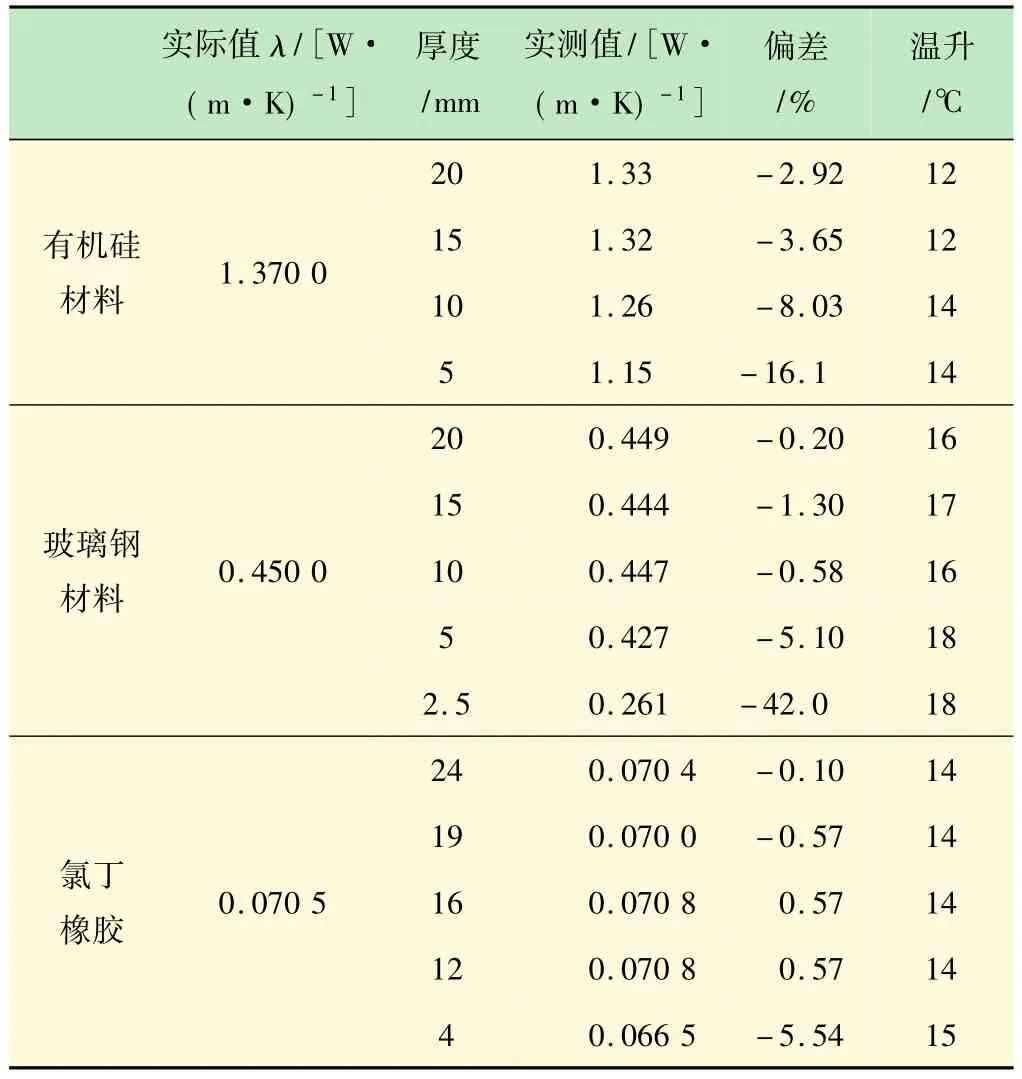
表2 不同厚度材料导热系数测试结果
4 结论
(1)在热带法测试材料导热系数时,往往存在厚度方向尺寸达不到制样要求的情况。同一材料,厚度不同,测量结果也不同,给实际测量带来了很大困扰。针对这一情况,采用fluent软件仿真计算出不同导热系数材料对应的最小可测量厚度,从而可以针对不同材料选取不同厚度测量,将低导热材料可测厚度从25 mm减小到5 mm甚至更薄(视材料本身导热大小而定),同时也减小了以往因材料厚度不足而叠加测量带来的接触热阻误差,扩大了可测材料的范围的同时还提高了测量精度。
(2)利用fluent软件,选用动量/质量守恒方程结合热传导方程,基于环境温度下测量导热系数,忽略热辐射及对流传热,忽略接触热阻,得到不同导热系数材料各自的最小可测量厚度,并利用自行搭建的测试设备选取了3种材料进行试验验证。结果表明,对于1.5 W/(m·K)以内的材料,25 mm的厚度可以达到理想的无限大介质要求,样品外表面温升小到几乎可以忽略;厚度越小,测试值越偏离实际值;导热系数越大,对应的最小可测量厚度越大。
(3)随着样品厚度的减小,测试值偏差越来越大,但有时偏高有时偏低,并不像模拟计算得到的越薄越偏小的趋势。这是由于计算时把厚度作为唯一的自变量去模拟,而在实际测量时往往有更多的误差因素,比如接触热阻的存在,样品边界的少量漏热,样品表面粗糙度,样品材质不均匀性以及数据拟合处理的误差等等都会引起测量的偏差。
[1]姚福娣.电站锅炉炉墙结构的设计研究[J].锅炉技术,2004,35(6):9-13,81.
[2]郑楚光,柳朝晖.大型电站锅炉实际运行工况的数值预报[J].中国电机工程学报,2000,20(6):79-83.
[3]路义萍,李伟力.大型空冷汽轮发电机转子温度场数值模拟[J].中国电机工程学报,2007,27(6):7-13.
[4]王桂兰,杨云珍.固体氧化物燃料电池三维热流电化学分析[J].中国电机工程学报,2007,27(8):99-103.
[5]皇甫艺,吴静怡.内燃发电机组冷热电联供系统集成式热管理器的设计[J].中国电机工程学报,2007,27(8):64-69.
[6]柯 磊,杨党强,袁艳红.稳态法测量导热系数的误操作影响分析[J].实验室研究与探索,2014(2):10-13.
[7]杨永华,曾 辉,陈美华.改进型导热系数测量仪的研制与实验[J].实验室研究与探索,2011(3):20-23,35.
[8]解俊梅,田淑英,侯方卓.稳态圆筒法测定材料的导热系数[J].实验室研究与探索,1997(3):44-47.
[9]Van der Held E F M,Van Druven F E.A Method of Measuring the Thermal Conductivity of Liquid[J].Physics,1949,15:866-869.
[10]Gracemann P.Measurement of Thermal Conductivities of Liquid by an Unsteady State Method[M].New York:Academic,1962.
[11]魏高升,刘育松.气凝胶及其复合绝热材料的导热系数测量[J].工程热物理学报,2011,32(4):667-670.
[12]王补宣,虞维平.热线法同时测定含湿多孔介质导热系数和导温系数的实验技术[J].工程热物理学报,1986,7(4):381-386.
[13]于帆,张欣欣.热线法测量半透明固体材料的导热系数[J].计量学报,1998,19(2):112-118.
[14]丁方圆,潘黎明,于 瑶,等.热线法测定气体导热系数实验的探讨与改进[J].物理实验,2014,24(12):39-41.
[15]程远贵,董岱峰,周 勇.等。耐火纤维毡的高温导热系数研究[J].化工设计,2001,11(2):22-23,41.
[16]范有明.热线法快速测量微粒导热系数的研究[J].工业计量,2006,16(6):1-3.

