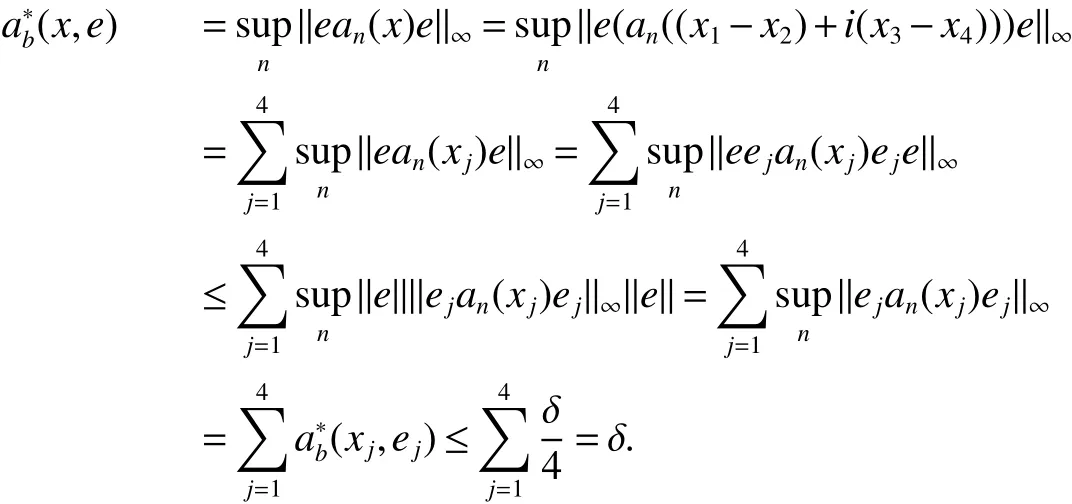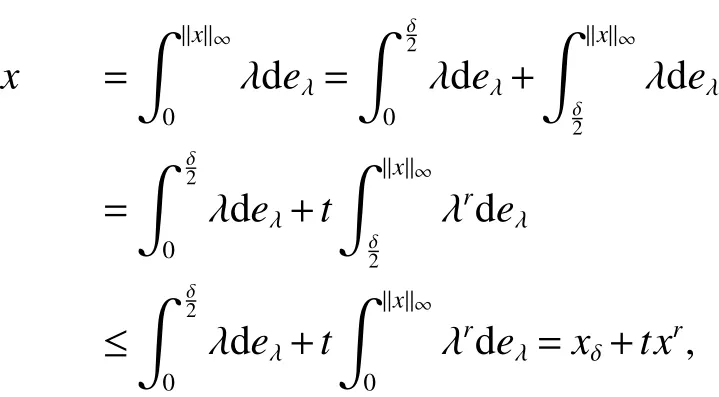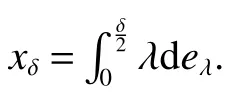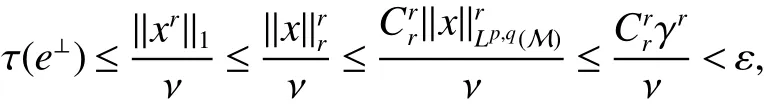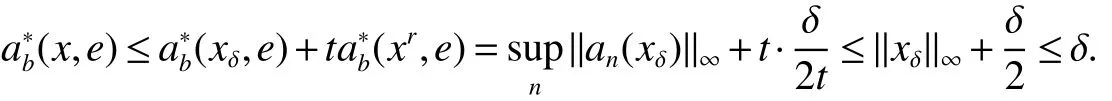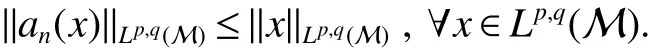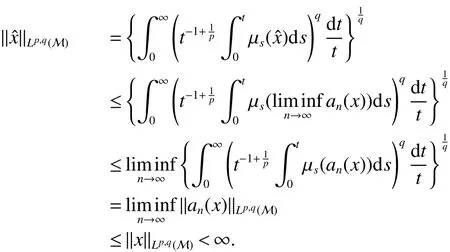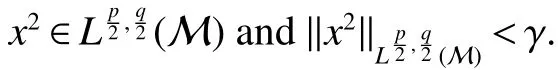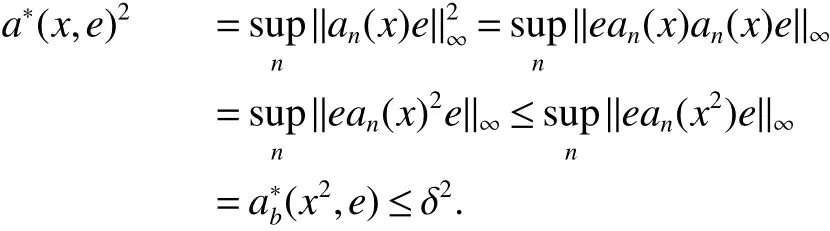Ergodic Theorems for Noncommutative Lorentz Spaces∗
Arxen T Yerkex,Turdebek N Bekjan
(College of Mathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang 830046,China)
0 Introduction
First,werecalltheclassicalLorentzspaces.Givenameasurespace(X,Σ,ν),let0 wheref∗(t)isthedecreasingrearrangementoff.TheclassicalLorentzspacesLp,q(X)isthesetallmeasurablefunctionsfon function(X,Σ,ν)with kfkLp,q(X)<∞.We refer to[1–4]for more information aboutLp,q(X). Using the operator space theory and theory of interpolation of Banach spaces,Junge and Xu[5]proved a noncommutative analogue of the classical Dunford-Schwartz maximal ergodic inequality for positive contraction onLp(M),and the analogue of Stein’s maximal inequality for symmetric positive contractions onLp(M),1 The purpose of this article is to present the individual ergodic theorems in the noncommutative Lorentz spaceLp,q(M). The remainder of this article is organized as follows.Section 2 contains some preliminaries and notations on the noncommutativeLp-spaces and noncommutative Lorentz spaces,including the noncommutative Lorentz spaces and their elementary properties.In section 3 we give some theorems,de finitions about uniform equicontinuity of sequences of operators.Finally,using the techniques in[7]we prove the individual ergodic theorems in noncommutative Lorentz spaceLp,q(M). We use standard notation and notions from theory of noncommutativeLpspaces.Our main references are[8–10](see[9]for more historical references).Let M be a finite von Neumann algebra on a Hilbert space H with a normal finite faithful trace τ and denote the lattice of(orthogonal)projections in M by P(M).The closed densely de fined linear operatorxin H with domainD(x)is said to be affiliated with M if and only ifu∗xu=xfor all unitary operatorsuwhich belong to the commutant M0of M.Ifxis affiliated with M,thenxis said to be τ-measurable if for every ε >0 there exists a projectione∈P(M)such thate(H)⊆D(x)and τ(e⊥)< ε(where for any projectionewe lete⊥=1−e).The set of all τ-measurable operators will be denoted byL0(M;τ)or simply byL0(M).The setL0(M)is a ∗-algebra with sum and product to be the respective closure of the algebraic sum and product. The measure topologytτinL0(M)is given by the system ε>0,δ>0,of neighborhoods of zero.Note that if one replaces the condition kxek∞≤ δ above by the generally weaker condition kexek∞≤ δ,then the corresponding family of neighborhoods of zero generates the same topologytτ(see[11]). The trace τ can be extended to the positive coneL+0(M)ofL0(M): Given 0 whereThen(M,k·kp)is a normed(or quasi-normed forp<1)space,whose completion is the noncommutativeLp-space associated with(M,τ),satisfying all the expected properties such as duality(see[9,10]),denoted byLp(M,τ)or simply byLp(M).As usual,we setL∞(M,τ)=M and denote by k·k∞(=k·k)the usual operator norm. Letxbe a τ-measurable operator andt>0.The ”t-th singular number(or generalizeds-number)”ofxµt(x)is de fined by It is clear that,ifxis a τ-measurable operator,then µt(x)< ∞ for everyt>0.See[8]for more information about generalized s number. We say that a sequence{xn}⊂L0(M)converges in measure tox∈L0(M),xn→x(m),if,given ε>0,δ>0,there is a numberN=N(ε,δ)such that for anyn≥Nthere exists a projectionen∈P(M)satisfying the conditions τ(e⊥n)< ε and k(xn−x)enk<δ. Accordingly,we also say that a sequence{xn}⊂L0(M)converges tox∈L0(M)almost uniformly(a.u.)(bilaterally almost uniformly(b.a.u.))if for every ε>0 there exists such ane∈P(M)that τ(e⊥) ≤ ε and k(x−xn)ek∞→ 0(respectively,ke(x−xn)ek∞→0).By Theorem 2.3 and Remark 2.4 of[11],we find that the algebraL0(M)is complete with respect to botha.u.andb.a.u.convergences. De finition 1Letxbe a τ-measurable operator affiliated with a semi- finite von Neumann algebra M,and 0 The set of allx∈L0(M)with kxkLp,q(M)<∞is denoted byLp,q(M)and is called the noncommutative Lorentz space with indicespandq. It is easy to check that(Lp,q(M),k·kLp,q(M))is a quasi-Banach space.Moreover,ifp>1,q≥ 1,and equipped with the equivalent norm that Remark 1(i)Ifp=q,thenLp,p(M)=Lp(M).(ii)Let 0 is dense inLp,q(M)(cf.[4]).Hence M is also dense inLp,q(M). A positive linear map α :L1(M)→L1(M)will be called an absolute contraction if α(x)≤ 1 and τ(α(x))≤ τ(x)for everyx∈M with 0≤x≤1.Note that,as it is shown in[6],kα(x)kp≤kxkpfor eachx=x∗∈S and all 1≤p≤∞.Besides,there exist unique continuous extensions α:Lp(M)→Lp(M)for every 1≤p≤∞.Its restriction α:M→M is ultra-weakly continuous.Note that since α is positive,it is hermitian i.e.α(x)∗=α(x∗)for allx∈L1(M). Lemma 1Let 1≤p<∞and 1≤q<∞.If α is the above absolute contraction,then Proof Letx=x∗∈M,by the formula on page 289 of[8],we have that Hence From this lemma follows that if 1≤p<∞,1≤q<∞,then α has unique continuous extension α :Lp,q(M)→Lp,q(M).Forx∈Lp,q(M),we denote LetXbe any set.Ifai:X→L0(M),i∈I,ande∈P(M)are such that{ai(x)e}i∈I⊂ M(respectively,{eai(x)e}i∈I}⊂M),we denote De finition 2Let(X,k·k)be a normed space andX0a subset ofXsuch that 0 ∈X0,where 0 is the neutral element ofX.A familyai:X→L0(M),i∈I,of additive maps is calleduniformly equicontinuous in measure(u.e.m.)(bilaterally uniformly equicontinuous in measure(b.u.e.m.))at 0 onX0,if,given ε>0,δ>0,there is such a γ >0 that for everyx∈X0with kxk<γ there existse∈P(M)for which Lemma 2Let 1 ProofLet us consider the bilateral case.The “only if”part is obvious.To prove the“if”part, fix ε>0 and δ>0.Then there is such a γ >0 thatx∈Lp,q+(M)and kxkLp,q(M)< γ imply thatfor some Letx∈Lp,q(M)with kxkLp,q(M)<γ.Then we can writex=x1−x2+i(x3−x4)such thatandSinceandthere existsej∈P(M)such thatand Thus,the assertion holds. Proposition 1If 1 ProofDue to Lemma 2,it is sufficient to show that{an}isb.u.e.m.at 0 onSince M+is dense inby Theorem 3.1 of[7],we only show that{an}b.u.e.m.at 0 on Fix ε >0 and δ>0,there exists such at=t(p,q,δ)thatt·λr≥ λ wheneverwherer=min{p,q}.Let ν>0 and γ>0 be such thatwhereCrsatis fies Letx∈M+satisfy kxkLp,q(M)≤γ,then andThen we derive Therefore,{an}isb.u.e.m.at 0 on(M+,k·kLp,q(M)). Theorem 1Let 1 Proof By Proposition 1,we know that{an}isb.u.e.m.at 0 on(Lp,q(M),k·kLp,q(M)),and by Theorem 4.2 of[7],for eachx∈M,the averages(1)convergeb.a.u..Applying Theorem 2.1 of[7],we have for eachx∈Lp,q(M)the averages(1)convergeb.a.u..Letis the b.a.u.limit of averages(1),then by Theorem 2.3 of[11],we know that∈L0(M).It implies that the averages(1)converge to∈L0(M)in measure,for eachx∈Lp,q(M).Similarly to the proof of Lemma 1,for eachn∈N+,we can prove that Applying Lemma 2.5 of[8]and Fatou lemma,we obtain Therefore∈Lp,q(M). Proposition 2Let 2 ProofBy Theorem 3.2 of[7]and Lemma 2,it is enough to show that{an}isu.e.m.at 0 on(M+,k·kLp,q(M)). Fix ε >0 and δ>0.Since,due to Proposition 1,it is sufficient to show that{an}isb.u.e.m.at 0 onthere exists such a γ >0 thatimply thatfor somee∈P(M)with Therefore,there ise∈P(M)such that τ(e⊥)≤ ε and(x2,e)≤δ2,applying Kadison’s inequality again,we arrive at Thus,a∗(x,e)≤δ. Theorem 2If 2≤p<∞,2≤q<∞,then for everyx∈Lp,q(M),the averages(1)converge a.u.to some∈Lp,q(M). ProofBy Corollary 4.1 of[7],the sequence{an(x)}convergesa.u.for everyx∈M.Since the set M is dense inLp,q(M),applying Theorem 2.1 of[7]and Proposition 2,we infer that the averagesanconvergea.u.for all∈Lp,q(M).The fact that the corresponding limitsbelong toLp,q(M)follows as in Theorem 1. References: [1]Cwikel M,Sagher Y.(L(p,∞))∗[J].Indiana Univ Math Journ,1972,21:781-786. [2]Grafakos L.Classical and Modern Fourier Analysis[M].London:Pearson Education,2004. [3]Hunt R A.OnL(p,q)spaces[J].L’Enseignement Math,1966,12:249-276. [4]Han Yazhou,Bekjan T N.The dual of noncommutative Lorentz spaces[J].Acta Math Sci,2011,31:2067-2080. [5]Junge M,Xu Q.Noncommutative maximal ergodic inequalities[J].J.Amer Math Soc,2007,20:385-439. [6]Yeadon F J.Ergodic theorems for semi finite von Neumann algebras[J].London Math Soc,1977,16:326-332. [7]Litvinov S.Uniform equicontinuity of sequences of measurable operators and non-commutative ergodic theorems[J].Proc Amer Math Soc,2012,140:2401-2409. [8]Fack T,Kosaki H.Generalized s-numbers of τ-measure operators[J].Pac J Math,1986,123:269-300. [9]Pisier G,Xu Q.NoncommutativeLp-spaces//Handbook of the Geometry of Banach Spaces[J].Amsterdam:North-Holland,2003,2:1459-1517. [10]Terp M.LpSpaces Associated with von Neumann Algebras[R].Notes,Copenhagen Univ,1981. [11]Chilin V,Litvinov S,Skalski A.A fewremarks in non-commutative ergodic theory[J].J Operator Theory,2005,53:331-350. [12]Shao Jingjing,Han Yazhou.Szeg¨o Type Factorization Theorem for Noncommutative Hardy-Lorentz Spaces[J].Acta Mathematica Scientia,2013,33(6):1675-1684.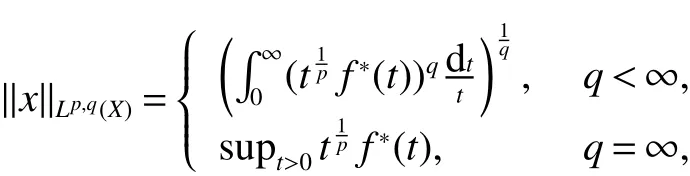
1 Preliminaries
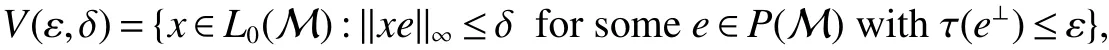
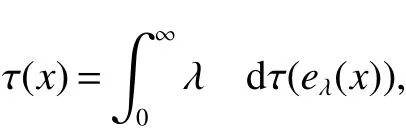
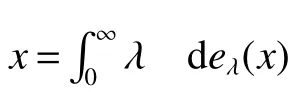
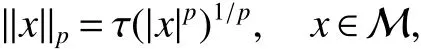
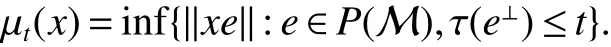
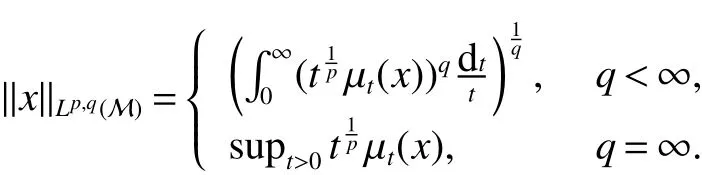
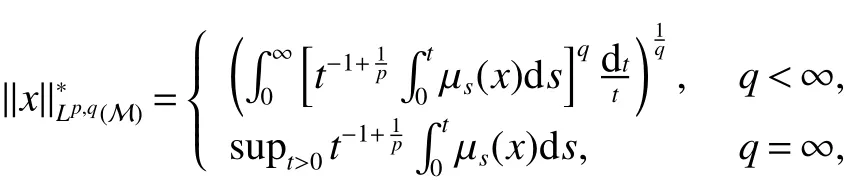
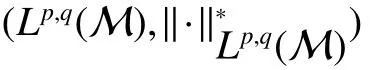

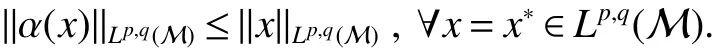
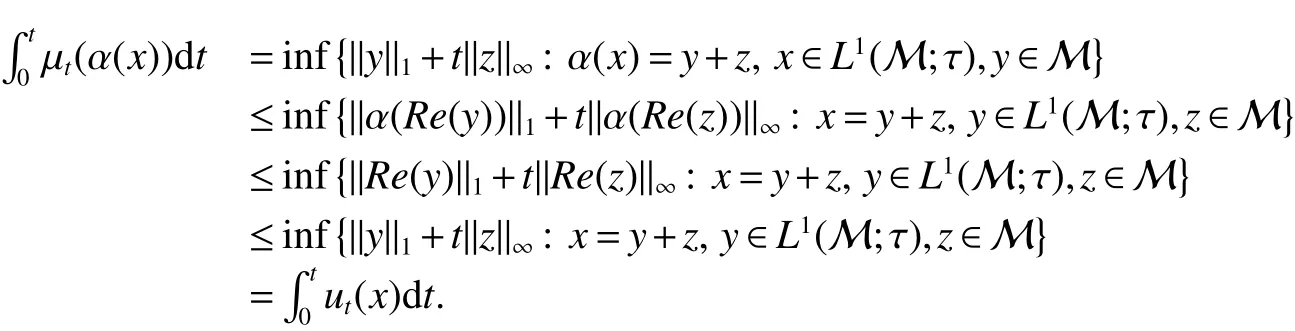


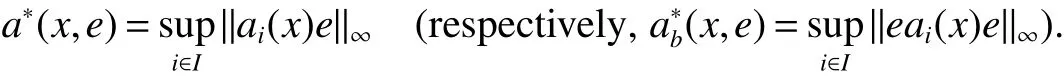
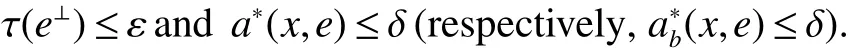
2 Ergodic theorems for noncommutative Lorentz spaces