基于连续折线索单元的树状结构找形研究

张 倩，陈志华，王小盾，刘红波

(1. 天津大学建筑工程学院，天津 300072；2. 天津市土木工程结构及新材料重点实验室，天津 300072)

基于连续折线索单元的树状结构找形研究

张 倩1,2，陈志华1,2，王小盾1,2，刘红波1,2

(1. 天津大学建筑工程学院，天津 300072；2. 天津市土木工程结构及新材料重点实验室，天津 300072)

在树状结构各种力学性能研究中，找形分析是十分重要的．在研究以往树状结构找形过程的基础上，以减小杆件内的单元弯矩为目的，提出将连续折线索单元应用于树状结构找形的方法，给出一般操作步骤，并通过试验对该方法进行验证．经过内力分析比较，得到该方法能够有效减小单元弯矩、结果较理想的结论，同时该方法具有操作简便、无需编程迭代、耗时较短的优势．对找形后的结果进行优化，可以进一步减小单元弯矩．分析分级节点位置变化对找形结果的影响，总结规律，为今后树状结构工程的设计应用提供了一定的参考.

树状结构；找形分析；连续折线索单元

树状结构由德国设计师Frei Otto于20世纪60年代提出，文献[1]介绍了树状结构这一结构形式，文献[2]从结构哲学的角度出发，在论述自然结构体的形成及原理，比较分析自然结构体和建筑结构体的基础上，提出了树状结构的研究方向．文献[3]简介了树状结构在公共建筑中的应用．文献[4]从建筑结构仿生入手，结合国内外工程实例，简要介绍了树状建筑结构及树状结构屋顶．文献[5-14]对树状结构的静动力分析进行了研究．文献[15-17]对树状结构的节点设计和制造进行了研究．文献[18-21]对树状结构的施工工艺和过程进行了探讨．

树状结构的形态关系的力学性能，如何使结构受力更为合理，使材料发挥最大功效，是值得关注和研究的．本文在总结各种树状结构找形方法的基础上，提出应用连续折线索单元对树状结构进行找形研究，并进行验证性试验．该方法能够有效减小杆件的单元弯矩，耗时较短，结果较理想．对节点荷载下的结构找形结果进行优化，进一步减小单元弯矩．研究分级节点位置变化对结构的影响．

1 树状结构找形研究进展

德国斯图加特大学、轻型结构研究所(IL-Frei Otto)、测量学工程应用研究所(IAGB-Klaus Link-witz)和结构力学研究所(IB-Ekkehard Ramm)在早期对树状结构找形进行了一些研究．文献[22]基于分杈角度、层数等参数编写程序来确定树状结构的形状．图1是利用这种程序产生的一种分杈角度为50°、层数为8的树状结构形式，这种找形方法对于显示树状结构杆件的不同布置很有效，但没有考虑结构的力学性能，因此只是一种单纯的生成形状的程序设计．文献[23]使用另一种程序设计方法CARAT探讨了不同荷载作用下内力为压力时的最优几何形状，发现树状结构更适用于低密度分布荷载情况．文献[24]使用如图 2的线模型探讨结构形状，将线模型浸入水中，表面张力使得细线聚拢到一起形成树的形状，即通过作用在细线上的表面张力寻找伪最小路径，使用这种方法产生的实际形状受到细线松弛量的影响．文献[25]对树状结构进行了广泛研究，将细线固定在框架上或在悬浮状态下拉伸，珠子在细线上通过摩擦力成为节点，不同于浸入水中的线模型，这种方法的优点是设计者可以通过滑动节点到不同位置迅速找到一系列几何形状，图3为使用串珠的三维线模型．

图1 分杈角度50°、层数为8的形状Fig.1 Shape with 50° branching angle，8 branching layers

图2 浸入水中的线模型Fig.2 Thread model dipped in water

图3 使用串珠的三维线模型Fig.3 3D thread model using beaded strings

文献[26]使用基于遗传算法的设计工具 IGDT，对内力为压力和拉力的两种状态，荷载位置分别在顶端和底部，中间节点是否约束的树状结构计算模型进行了分析，并与传统浸水线模型进行了比较，同样的计算模型也被用来寻找构件总长度最小的几何形状．文献[27]利用浸水线模型对密歇根州花园中心树屋的树状支承柱进行找形分析，得到更加适用于此工程的小比例模型(见图 4)．文献[28]基于自平衡理论，假定模型节点为铰接，在节点处添加支座，并调整其竖向位置以得到静定结构，再调整其水平位置使得支座反力接近为零，得到结构最终模型(见图 5)，并将程序计算的找形结果与浸水线模型对比．

图4 树屋支承柱1∶100模型Fig.4 1∶100 model of tree house

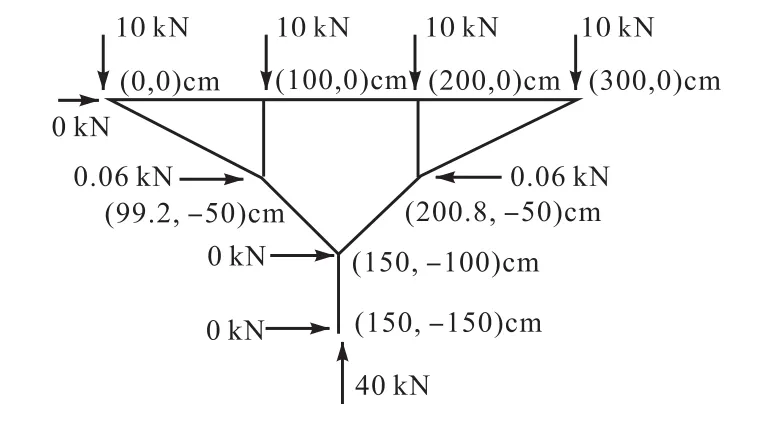
图5 自平衡模型Fig.5 Shape of self equilibrium

文献[29]将线模型倒挂(见图 6)，利用倒挂受拉反向受压的原理进行找形．文献[30]用改进的进化论方法(evolutionary structural optimization，ESO)创建结构形态，生成了树状结构模型，如图7所示．

图6 倒挂模型Fig.6 Reverse hanging model

图7 ESO模型效果图Fig.7 Effect drawing of model using ESO

文献[31-32]基于形效结构的概念，通过分析树状结构的几何特点和受力特点，提出了一种树状结构的找形方法逆吊递推找形法，当所有高级树枝均指向由其分出的低级树枝所承担的屋盖受力中心时，各级树枝均只受轴力作用，所有节点处均无弯矩产生，并明确了具体实施步骤和需要注意的问题，结合树状结构工程实例，介绍了逆吊递推找形法的实际应用过程，并对稳定性分析和设计方法进行了研究．文献[33]以树状结构的最小用钢量为目标函数，以结构的强度、刚度、稳定性为约束条件，对树状结构进行优化分析，优化后在减少结构用钢量的同时，也减小了结构的最大竖向位移，并使各杆件的内力分布更趋合理．文献[14]也介绍了ESO优化法的应用，并以一单层树状结构为例进行找形过程和结果分析．

2 连续折线索单元应用于树状结构的找形

树状结构力流明确，通过高级树枝逐级传递，将屋面荷载有效集中到基础，树枝的分布即杆件的力流传递方向，在进行杆件布置即找形分析时，树枝只受轴力、节点处无弯矩是较理想状态，因此尽可能减小杆件内弯矩是本文找形的主要目的．传统的浸水模型并不能找到唯一的形状，操作起来也较不简便；串珠模型和倒挂模型可以找到一系列的形状，并由设计师根据一些客观条件如美观因素等选择一个最终形态，而往往不是受力上最为合理的形态．以上物理找形方法都利用了丝线的只拉特性，很好地模拟了树状结构单元轴力是主要控制因素的特性，但形态不唯一；现有的数值模拟方法可以得到唯一解，但均需通过一步步的迭代使得单元内的弯矩较小．本文综合考虑以上找形方式的优势和不足，提出基于连续折线索单元的树状结构找形方法．该方法的理论依据来源于逆吊找形法，其基本思想为将特定荷载下的柔性结构固化，翻转后即可获得在相同荷载下只承受压力作用的结构．连续折线索单元各节点间的索段可以不在同一直线上，呈折线布置，除两端节点外各节点可在外力作用下沿单元任意滑动以达到平衡状态[34]．根据连续折线索单元的受力特点，推导单元刚度矩阵，编写 ABAQUS用户单元子程序，将子程序嵌入软件，从而实现连续折线索单元的调用．根据节点个数n命名为n节点连续折线索单元，应用于树状结构找形上，各节点均可滑动以达到平衡．索段只受轴力，满足树状结构力学模型，节点在外力作用下滑移达到平衡状态的过程即找形过程．

本文以一简单二维树状结构为例说明应用连续折线索单元的树状结构找形过程．图 8是 2级分杈树状结构的初始形状，节点 8固定，各节点坐标如图8所示．上部节点受拉、下部节点固定和下部节点受拉、上部节点固定两种情况下，应用连续折线索单元的找形结果是一致的，因此本文采用上部节点固定、下部节点受拉的模型进行找形分析．

图8 2级分杈树状结构初始形状(单位：m)Fig.8 Initial shape of tree structure with two-level branching(unit：m)

首先考虑静力计算过程找形，在最下端节点8施加力的荷载，在找形过程中连续折线索单元的可滑移节点会产生大变形，导致计算结果不收敛．再考虑在最下端节点8施加位移荷载，具体找形过程如下：

(1)结构组成，结构由3个3节点连续折线索单元和 1个两节点连续折线索单元组成，节点 1、5、2为单元1，节点3、6、4为单元2，节点5、7、6为单元3，节点7、8为单元4；

(2)节点1、2、3、4固定，建立10个荷载步，在节点8作用竖向位移荷载，取值分别为1,m、2,m、3,m、4,m、5,m、6,m、7,m、8,m、9,m和10,m，查看每一步的支座反力，第1步支座反力为零，拉索处于松弛状态，第2步开始反力不为零，拉索处于张拉受力的状态；

(3)在位移荷载 1.1～2.0,m范围内再建立10个荷载步，每一步位移荷载增量为 0.1,m，查看支座反力，按照步骤(2)的方法选取下一轮10个荷载步范围1.41～1.50,m，每一步位移荷载增量为0.01,m；

(4)选取所有支座反力均不为零的最小荷载步，位移荷载为 1.450,m，根据该荷载步中各节点位移确定各节点位置，形成如图9所示的找形结果．

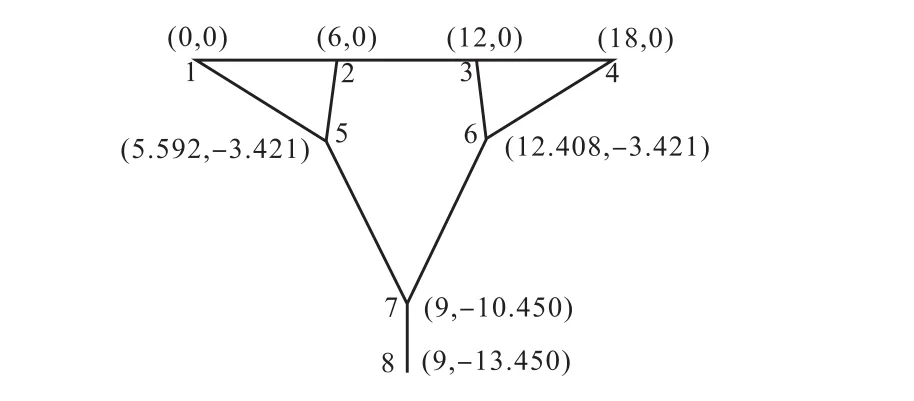
图9 基于静力计算的找形结果(单位：m)Fig.9 Final shape using static calculation(unit：m)

上述找形过程需要3～4轮多个荷载步的选取和计算，因此考虑加质量块的动力分析进行更加简便的找形过程，因为动力分析时考虑一定阻尼，能够解决静力分析时节点大变形导致的不收敛问题．其具体找形过程如下：

(1)结构组成，结构由3个3节点连续折线索单元和 1个两节点连续折线索单元组成，节点 1、5、2为单元1，节点3、6、4为单元2，节点5、7、6为单元3，节点7、8为单元4；

(2)节点1、2、3、4固定，在可滑移节点5、6、7、8处加质量块单元，质量大小为0.1,N，单元阻尼大小1.0，在节点8的质量块上作用一竖直向下1,N的荷载；

(3)进行结构计算，根据各节点位移确定最终状态的各节点位置，形成如图10所示的找形结果．折线索单元应用于树状结构找形方法的可行性．

图12 试验找形后形状Fig.12 Final shape of test

对基于连续折线索单元确定形状的树状结构在Midas软件里进行静力计算，图13所示为单元编号，采用梁单元模拟，上部节点作用大小为10,kN/m的节点荷载，树状结构底部全固结，如图14所示，找形前后的弯矩计算结果如表1所示，将两者的弯矩进行比较，结果如图15所示．

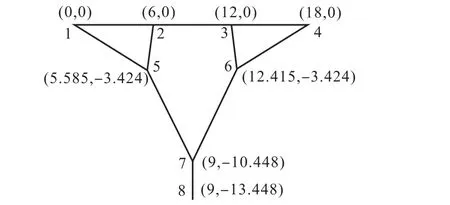
图10 基于动力计算的找形结果(单位：m)Fig.10 Final shape using dynamic calculation(unit：m)

由图9和图10可知，静力计算加位移荷载的找形方法和动力计算加质量块的找形方法在结果上非常相似，前者耗时比后者稍长，后者在一定程度上考虑了摩擦阻尼，二者各有优势，均能得到比较满意的找形结果．

为了对此数值模拟方法进行验证，进行简单试验．图 11所示为找形前的初始形状，用表面稍光滑有一定摩擦的线来模拟连续折线索单元，用不同质量的水袋来模拟加在质量块上的不同荷载，节点 5、6的水袋质量是节点8的5倍，此平衡状态为结构初始形态；去掉节点5、6的水袋，节点5、6、7、8在节点8水袋质量的作用下滑动达到新的平衡，如图 12所示，此平衡状态即为找形后的结构形状．由此简单试验得到的结果与数值模拟方法很接近，验证了将连续

图11 试验初始形状Fig.11 Initial shape of test

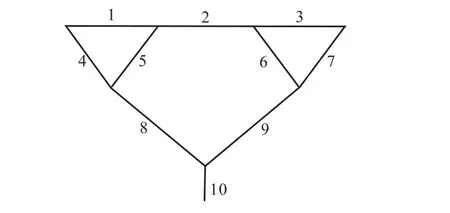
图13 2级分杈树状结构单元编号Fig.13 Element numbers of tree structures with two-level branching

表1 节点荷载作用下2级分杈找形前后弯矩比较Tab.1 Comparison of bending moment with two-level branching before and after form-finding under nodal loads

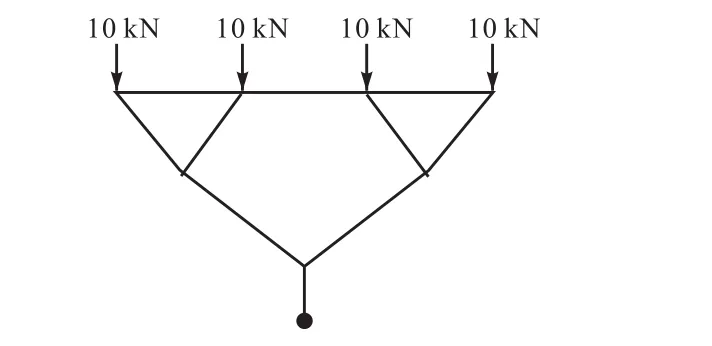
图14 2级分杈树状结构节点荷载Fig.14 Tree structures with two-level branching under nodal loads

图15 2级分杈节点荷载作用下找形前后弯矩比较Fig.15 Comparison of bending moments with two-level branching before and after form-finding under nodal loads

由表1和图15可知，经过找形后的单元弯矩明显减小，对于树状结构的分级树枝单元，减小幅度为70.56%～83.98%，为使总荷载大小相等，可在单元1、2、3作用大小为2.22,kN/m的均布线荷载代替原节点荷载．弯矩比较结果如表 2和图 16所示，可知均布荷载下，找形后的单元弯矩也明显减小，对于分级树枝单元，减小幅度最高达 91.65%，说明基于连续折线索单元的找形方法应用于树状结构是可行的，能够有效减小杆件单元内的弯矩．

表2 均布荷载作用下2级分杈找形前后弯矩比较Tab.2 Comparison of bending moment with two-level branching before and after form-finding under uniform loads

图16 2级分杈均布荷载作用下找形前后弯矩比较Fig.16 Comparison of bending moments with two-level branching before and after form-finding under uniform loads

根据以上过程，对应用连续折线索单元找形树状结构的动力计算步骤总结如下：

(1) 结构组成，将初始形态的结构划分为连续折线索单元组成的结构形式；

(2) 在可滑移节点处加质量块单元，确定质量大小和单元阻尼大小，通常阻尼不小于 1.0，也不可过大，找形无关外力，因此忽略结构上部荷载作用，在最下端节点的质量块上作用一竖直向下的荷载，荷载大小至少是质量块质量的10倍，上部节点固定；

(3)进行结构计算，根据各节点位移确定最终状态的各节点位置，完成找形过程．

需要说明的是：应用连续折线索单元找形，利用的是节点的可滑移性以达到平衡状态，如果静力计算直接加力的荷载，会因为节点的大变形导致计算不收敛，因此考虑采用在可滑移节点处加质量块和单元阻尼进行动力计算，在加载时荷载大小至少是质量块质量的10倍以上也是为了克服阻尼以达到最终的找形形态．如采用静力分析计算，在最下端节点加位移荷载，通过上部节点支座反力的变化，逐渐缩小位移荷载范围，经过几轮选取，也可找到最终的几何形状，二者的找形结果吻合度很高．

应用连续折线索单元进行树状结构找形有如下优势：只拉单元模拟，受力合理；概念清晰，操作简便，不需迭代编程，耗时较短；有效减小弯矩，结果较理想，具有在工程中广泛推广的意义．

再以3级分杈树状结构为例，比较找形前后的单元内弯矩．3级分杈树状结构初始形状及节点坐标值如图 17所示，按照上述方法找形后的形状如图 18所示．

图17 3级分杈树状结构初始形状(单位：m)Fig.17 Initial shape of tree structure with three-level branching(unit：m)

图18 3级分杈树状结构找形结果Fig.18 Final shape of tree structure with three-level branching

对基于连续折线索单元确定形状的 3级分杈树状结构在Midas软件里进行静力计算，如图19所示为单元编号，采用梁单元模拟，节点1、4、5、8作用大小为 10,kN/m的节点荷载，树状结构底部全固结，弯矩比较结果如表3和图20所示，如果在单元1～7作用大小为2.22,kN/m的均布线荷载，弯矩比较结果如表4和图21所示．

表3 节点荷载作用下3级分杈找形前后弯矩比较Tab.3 Comparison of bending moment with three-level branching before and after form-finding under nodal loads

图19 3级分杈树状结构单元编号Fig.19 Element numbers of tree structure with three-level branching

由表3、表4、图20和图21可知，经过找形后的单元弯矩明显减小，节点荷载作用下分级树枝单元的弯矩减小幅度为 12.15%～87.98%，均布荷载下弯矩减小幅度最高达 92.09%，说明应用连续折线索单元对树状结构进行找形的方法同样适用于 3级分杈树状结构，结果较理想．

图20 3级分杈节点荷载作用下找形前后弯矩比较Fig.20 Comparison of bending moments with three-level branching before and after form-finding under nodal loads

表4 均布荷载作用下3级分杈找形前后弯矩比较Tab.4 Comparison of bending moment with three-level branching before and after form-finding under uniform loads

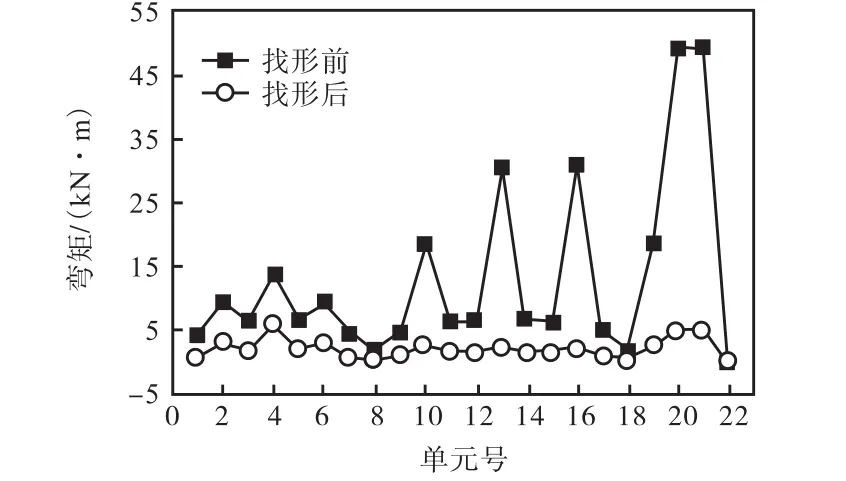
图21 3级分杈均布荷载作用下找形前后弯矩比较Fig.21 Comparison of bending moment with three-level branching before and after form-finding under uniform loads

为说明结论的普遍适用性，对不同初始形状的树状结构按照基于连续折线索单元的找形方法进行找形，并对找形前后的单元弯矩进行比较．2级分杈树状结构和 3级分杈树状结构的节点编号分别见图 8和图 17，不同初始形状的树状结构找形前后弯矩比较如表5所示．

表5 不同初始形状树状结构找形前后弯矩比较Tab.5 Comparison of bending moment of tree structures with different initial shapes before and after formfinding

由表 5可知，找形后的单元弯矩均有所减小，大部分减小幅度在80%以上，说明基于连续折线索单元的找形方法应用于树状结构是可行的，效果比较理想，具有普遍适用性．

3 优化方法

在荷载总值相等的前提下，对节点荷载和均布荷载作用下找形后结构的单元弯矩进行比较．以第 2节中的两个模型为例，2级分杈树状结构在两种荷载情况下的弯矩比较如图 22所示，3级分杈树状结构的弯矩比较如图23所示．

图22 2级分杈节点荷载和均布荷载下找形后弯矩比较Fig.22 Comparison of bending moment with two-level branching under nodal loads and uniform loads

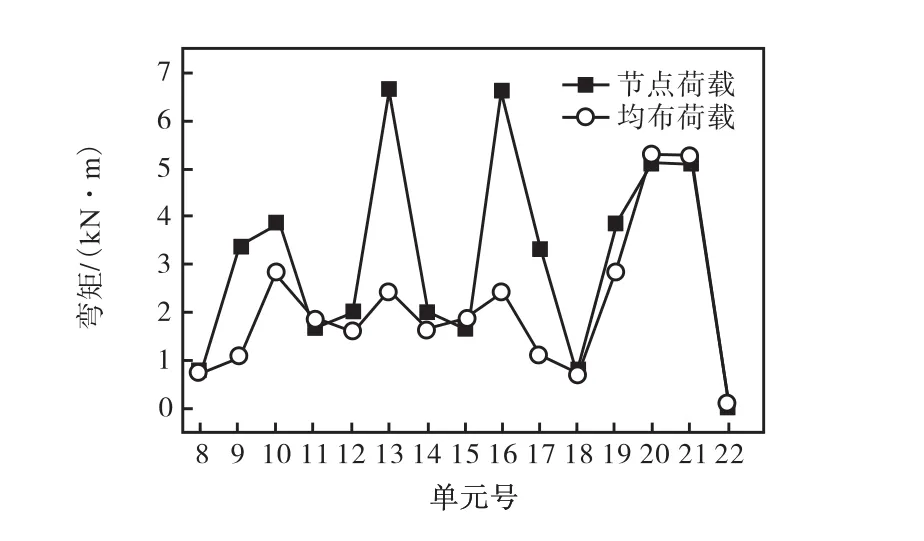
图23 3级分杈节点荷载和均布荷载下找形后弯矩比较Fig.23 Comparison of bending moment with three-level branching under nodal loads and uniform loads

由图22和图23可知，2级分杈树状结构和3级分杈树状结构找形后的结构在均布荷载下树枝单元弯矩值绝大部分小于节点荷载下的弯矩值，因此本节以2级分杈树状结构为例，探讨节点荷载下结构的优化，以期进一步减小单元弯矩值．

将图8所示的2级分杈树状结构增加级数，1级节点和2级节点位置不变，在2级节点和上部节点之间增加3级节点，形成如图24所示的3级分杈树状结构．对此 3级分杈结构按照第 2节的方法进行找形，找形结果如图25所示．

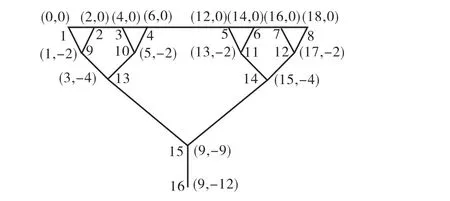
图24 3级分杈树状结构初始形状(单位：m)Fig.24 Initial shape of tree structure with three-level branching(unit：m)

图25 3级分杈树状结构找形结果Fig.25 Final shape of tree structure with three-level branching

保留找形后的2级节点，将3级节点、2级树枝和3级树枝去掉，2级节点和上部节点直接相连形成新的2级树枝，完成3级到2级的简化过程，形成如图26所示优化后的形状．

图26 优化后的找形结果(单位：m)Fig.26 Final shape after optimization(unit：m)

将原找形结果和优化后结果的单元弯矩进行比较，如图27所示，可知优化后各个杆件的弯矩均有所减小，减小幅度为37.89%～44.92%，结果比较理想．

综上，节点荷载作用下，首先对 2级分杈树状结构增加级数，形成 3级分杈树状结构；按照连续折线索单元应用于树状结构的找形方法进行 3级分杈的找形；去掉找形后的3级节点、3级树枝和2级树枝，将找形后的2级节点和上部节点直接相连，简化成新的2级树枝，形成优化后的形状．按照此优化方法形成的找形结果能够进一步减小节点荷载下的单元弯矩，效果较理想．均布荷载作用下，采用此优化方法并不能进一步减小弯矩，因此该优化方法适用于节点荷载作用下的树状结构找形结果的优化．

图27 2级分杈节点荷载作用下优化前后弯矩比较Fig.27 Comparison of bending moment with two-level branching before and after optimization under nodal loads

4 最优形状的讨论

树状结构初始形状的分级节点位置不同，找形结果会不同，对结构的内力也会有影响．本节以2级分杈树状结构为例，探讨1级节点和2级节点竖向坐标的变化对单元内弯矩的影响．

4.1 节点荷载

以图8所示的2级分杈树状结构为例，2级节点竖向坐标－4不变，1级节点竖向坐标分别为－7、－9和－11，以形状1、形状2和形状3代表3种情况，节点荷载作用下找形后的树枝单元弯矩比较如图28所示．

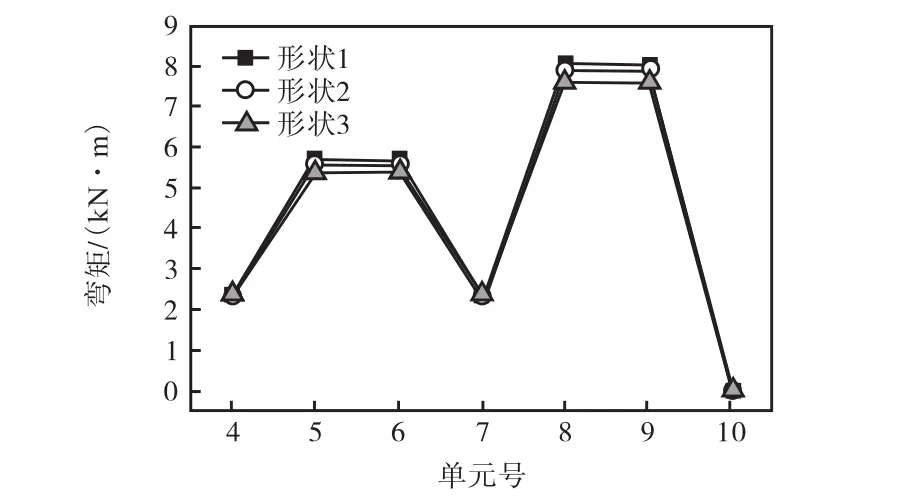
图28 节点荷载作用下1级节点变化时找形后弯矩比较Fig.28 Comparison of bending moment with the change of the first-level joint under nodal loads

由图28可知，节点荷载作用下，1级节点位置下移，找形后树枝单元弯矩减小，但相差不大．

1级节点竖向坐标－11不变，2级节点竖向坐标分别为-4、-5和-6，以形状1、形状2和形状3代表3种情况，节点荷载下找形后的树枝单元弯矩比较如图29所示．

由图 29可知，节点荷载下 2级节点位置下移，找形后树枝单元弯矩减小．

1级节点竖向坐标分别为-9、-10和-11，相应的2级节点竖向坐标分别为-4、-5和-6，即1级节点和2级节点竖向坐标差不变，以形状1、形状2和形状3代表3种情况，节点荷载作用下找形后的树枝单元弯矩比较分别如图30所示．

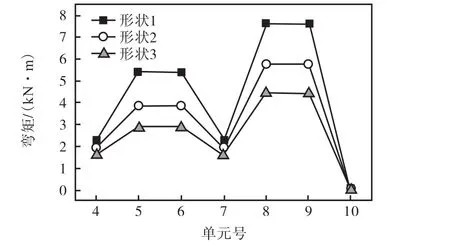
图29 节点荷载作用下2级节点变化时找形后弯矩比较Fig.29 Comparison of bending moment with the change of the second-level joint under nodal loads

图30 节点荷载作用下1、2级节点变化时找形后弯矩比较Fig.30 Comparison of bending moment with the change of the first- and second-level joint under nodal loads

由图30可知，节点荷载作用下1、2级节点位置均下移，找形后树枝单元弯矩减小．

4.2 均布荷载

与第 4.1节的节点位置相同，均布荷载作用下 3种变化的树枝单元弯矩比较如图31～33所示．

由图31～33可知，均布荷载作用下，1级节点位置下移，找形后树枝单元弯矩增加；2级节点位置下移，找形后大部分树枝单元弯矩增加；1、2级节点位置均下移，1级树枝和 2级树枝中间杆件的弯矩增加，2级树枝两侧杆件弯矩值略有减小．

综上，节点荷载作用下，1级节点位置下移，树枝单元弯矩减小；2级节点位置下移，树枝单元弯矩减小．均布荷载作用下，1级节点位置下移，树枝单元弯矩增加；2级节点位置下移，大部分树枝单元弯矩增加．因此，在确定找形之前的初步形状时，节点荷载作用下，分级节点的位置应在满足其他要求的情况下尽可能下移；而均布荷载作用下，分级节点的位置应在满足其他要求的情况下尽可能上移，这样找形后的树枝单元弯矩较小，结果较理想．

图31 均布荷载作用下1级节点变化时找形后弯矩比较Fig.31 Comparison of bending moment with the change of the first-level joint under uniform loads

图32 均布荷载作用下2级节点变化时找形后弯矩比较Fig.32 Comparison of bending moment with the change of the second-level joint under uniform loads

图33 均布荷载下作用1、2级节点变化时找形后弯矩比较Fig.33 Comparison of bending moment with the change of the first- and the second-level joint under uniform loads

5 结 论

在树状结构各种力学性能的研究中，找形分析是十分重要的，本文对此进行了一些研究比较，得到了如下结论：

(1) 基于连续折线索单元，提出了一种高效的树状结构找形方法，给出一般步骤，并通过试验进行验证；

(2) 节点荷载下，对 2级分杈树状结构进行优化，先增加级数找形，再简化成 2级分杈，优化后的单元弯矩进一步减小．

(3) 节点荷载下，分级节点位置下移，树枝单元弯矩值减小；均布荷载下，分级节点位置上移，树枝单元弯矩值减小；

(4) 本文的研究仅以二维树状结构为例，基于连续折线索单元的树状结构找形思路同样适用于三维树状结构，有待于进一步研究分析．

［1］ 陈志华. 索、玻璃及树状结构体系[J]. 建筑知识，2001(2)：41-44.

Chen Zhihua. Cable，glass and tree structures[J]. Architectural Knowledge，2001(2)：41-44(in Chinese).

［2］ 王小盾，余建星，陈质枫，等. 树状结构[J]. 工业建筑，2002(增)：553-555.

Wang Xiaodun，Yu Jianxing，Chen Zhifeng，et al. Tree structures[J]. Industrial Construction， 2002 (Suppl)：553-555(in Chinese).

［3］ 蔡长赓. 树状结构在公共建筑中的应用[J]. 工程建筑与设计，2002(3)：34.

Cai Changgeng. Application of tree structures in public buildings[J]. Construction and Design for Project， 2002(3)：34(in Chinese).

［4］ 龙文志. 浅介树状建筑结构[J]. 中国建筑装饰装修，2006(1)：188-193.

Long Wenzhi. An introduction of dendriform architectural structure[J]. Interior Architecture of China，2006(1)：188-193(in Chinese).

［5］ 罗永赤. 钢管树状柱的有限元分析[J]. 钢结构，2005，20(6)：46-49.

Luo Yongchi. Finite element analysis of dendriformcolumn[J]. Steel Construction，2005，20(6)：46-49(in Chinese).

［6］ 罗永赤. 钢管树状柱在垂直荷载作用下的手算分析[J]. 建筑技术开发，2008(3)：10-12.

Luo Yongchi. Hand calculation of dendriform-column under vertical loads[J]. Building Technique Development，2008(3)：10-12(in Chinese).

［7］ 王明贵，颜 锋. 钢管树状结构设计[J]. 钢结构，2006，21(6)：47-49.

Wang Minggui，Yan Feng. Design on the dendritic structure with steel tubes[J]. Steel Construction，2006，21(6)：47-49(in Chinese).

［8］ 张金铭，蔺俊强，陈思作. 空间树状结构设计[J]. 工业建筑，2007(增)：439-443.

Zhang Jinming，Lin Junqiang，Chen Sizuo. Design of tree structures[J]. Industrial Construction，2007(Suppl)：439-443(in Chinese).

［9］ 陈 俊，张其林，谢步瀛. 树状柱在大跨度空间结构中的研究和应用[J]. 钢结构，2010，25(3)：1-4，21.

Chen Jun，Zhang Qilin，Xie Buying. Research and application of dendritic column in long-span spatial structure[J]. Steel Construction，2010，25(3)：1-4，21(in Chinese).

［10］ 王忠全，陈 俊，张其林. 仿生树状钢结构柱设计研究[J]. 结构工程师，2010，26(4)：21-25.

Wang Zhongquan，Chen Jun，Zhang Qilin. Research on design of dendritic columns in bionic steel structures[J]. Structural Engineers，2010，26(4)：21-25(in Chinese).

［11］ 李 萌. 钢管树状柱的极限承载力分析[J]. 山西建筑，2012，38(20)：51-52.

Li Meng. On analysis of ultimate bearing capacity of dendriform-column[J]. Shanxi Architecture，2012，38(20)：51-52(in Chinese).

［12］ 马洪步，沈 莉，高博青，等. 钢管树状仿生结构的稳定性设计[J]. 建筑结构，2009，39(12)：97-99.

Ma Hongbu，Shen Li，Gao Boqing，et al. Stability design on the dendritic structure with steel tubes[J]. Building Structure，2009，39(12)：97-99(in Chinese).

［13］ 李法善，张 岚，蒋丽华，等. 三级分枝钢管树状结构有限元动力特性分析[J]. 钢结构，2012，27(5)：26-28.

Li Fashan，Zhang Lan，Jiang Lihua，et al. Finite element analysis of dynamic characteristics for tree steel pipe structure with three-level branches[J]. Steel Construction，2012，27(5)：26-28(in Chinese).

［14］ 徐 荣. 树状结构形态分析及其水平地震响应研究[D]. 上海：同济大学土木工程学院，2005.

Xu Rong. Morphology Analysis and Response Research Under Horizontal Earthquake Action of Tree Structures [D]. Shanghai：College of Civil Engineering，Tongji University，2005(in Chinese).

［15］ 萨鹏程. 树状结构空间节点性能研究[D]. 哈尔滨：哈尔滨工程大学航天与建筑工程学院，2009.

Sa Pengcheng. The Property Analysis of Dendriform Structure Space Joint[D]. Harbin：College of Aerospace and Civil Engineering ， Harbin Engineering University，2009(in Chinese).

［16］ 鲍广鉴，王 宏，徐重良，等. 树枝结构及巨型铸钢的应用与研究——深圳文化中心钢结构施工技术[J].钢结构，2003，18(6)：15-18.

Bao Guangjian，Wang Hong，Xu Zhongliang，et al. Use and study of dendritic structure and glant cast steelnode——Construction technique for Shenzhen cultural center[J]. Steel Construction，2003，18(6)：15-18(in Chinese).

［17］ 谭德远. 黄金树结构两种节点可选方案的性能比较[J]. 钢结构，2002，17(3)：19-20.

Tan Deyuan. Comparison to the properties of two joint plans of gold-tree structure[J]. Steel Construction，2002，17(3)：19-20(in Chinese).

［18］ 谭仲毅. 树状结构施工技术研究与应用[D]. 重庆：重庆大学土木工程学院，2002.

Tan Zhongyi. Construction Technical Research and Application of Tree Structures[D]. Chongqing：College of Civil Engineering，Chongqing University，2002(in Chinese).

［19］ 鲍广鉴，谭仲毅. 深圳文化中心黄金树安装技术[J].施工技术，2002，31(5)：6-8.

Bao Guangjian，Tan Zhongyi. Installation technology for the gold tree of Shenzhen culture center[J]. Construction Technology，2002，31(5)：6-8(in Chinese).

［20］ 鲍广鉴，周忠明. 深圳文化中心黄金树铸钢节点焊接技术[J]. 施工技术，2002，31(11)：18-20.

Bao Guangjian，Zhou Zhongming. Welding technology for cast steel joints of the gold tree of Shenzhen culture center[J]. Construction Technology，2002，31(11)：18-20(in Chinese).

［21］ 黄崇灿，张汉深. 树枝结构安装技术分析[J]. 城市住宅，2009(7)：112-113.

Huang Chongcan，Zhang Hanshen. Installation technology of tree structures[J]. City Residence，2009(7)：112-113(in Chinese).

［22］ Neureither M. The calculation generated from branch structure[C]//Branch Structure，Natural Structure-Lightweight Design in Architecture and Nature. 1992，4，SFB230：57-63.

［23］ Bletzinger K U. The optimization of branch structure [C]//Branch Structure，Natural Structure-Lightweight Design in Architecture and Nature. 1992，4，SFB230：65-70.

［24］ Kolodziejczyk M. Branch structure and thread：Some aspects of formation through thread model[C]// Branch Structure，Natural Structure-Lightweight Design in Architecture and Nature. 1992，4，SFB230：101-126.

［25］ Kennicke J. Structural trees：Comments on some fundamental design and construction aspects of tree-like branching columns[C]// Bulletin of the International Association for Shell and Spatial Structures. 1995：124.

［26］ von Buelow P. A Geometric Comparison of Branching Structures in Tension and Compression Versus Minimal Paths[Z]. IASS，2007.

［27］ von Buelow P. Breeding bridges：Genetic based form exploration[C]//International Symposium on New Olympics New Shell and Spatial Structures. Beijing，China，2006.

［28］ Hunt J，Haase W，Sobek W. A design tool for spatial tree structures[J]. Journal of the International Association for Shell and Spatial Structures，2009，50(1)：3-10.

［29］ 马千里. 树状结构研究[D]. 日本东京：法政大学，1997.

Ma Qianli. Research on Tree Structure[D]. Tokyo，Japan：Hosei University，1997(in Japanese).

［30］ 崔昌禹，严 慧. 结构形态创构方法——改进进化论方法及其工程应用[J]. 土木工程学报，2006，39 (10)：42-47.

Cui Changyu，Yan Hui. An advanced structural morphosis technique——Extended evolutionary structural optimization method and its engineering applications[J]. China Civil Engineering Journal，2006，39(10)：42-47(in Chinese).

［31］ 武 岳，张建亮，曹正罡. 树状结构找形分析及工程应用[J]. 建筑结构学报，2011，32(11）：162-168.

Wu Yue，Zhang Jianliang，Cao Zhenggang. Formfinding analysis and engineering application of branching structures[J]. Journal of Building Structures，2011，32(11）：162-168(in Chinese).

［32］ 张建亮. 树状结构形态分析与工程应用[D]. 哈尔滨：哈尔滨工业大学土木工程学院，2011.

Zhang Jianliang. Morphological Analysis and Engineering Applications of Branching Structures[D]. Harbin：School of Civil Engineering，Harbin Institute of Technology，2011(in Chinese).

［33］ 张金铭，陈思作，蔺俊强. 钢管树状支撑结构的形态分析[J]. 武汉大学学报：工学版，2009，42(2)：240-243.

Zhang Jinming，Chen Sizuo，Lin Junqiang. Morphological analysis of steel pipe dendritic supporting structure[J]. Engineering Journal of Wuhan University，2009，42(2)：240-243(in Chinese).

［34］ 毋英俊. 连续折线索单元及节点研究[D]. 天津：天津大学建筑工程学院，2010.

Wu Yingjun. Analysis of Sliding Cable Element and Node[D]. Tianjin：School of Civil Engineering，Tianjin University，2010(in Chinese).

(责任编辑：樊素英)

Form-Finding of Tree Structures Based on Sliding Cable Element

Zhang Qian1,2，Chen Zhihua1,2，Wang Xiaodun1,2，Liu Hongbo1,2
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory of Civil Engineering Structure and New Materials，Tianjin 300072，China)

Form-finding is very important in the researches on the mechanical behavior of tree structures. Based on the researches of other form-finding methods of tree structures，a new form-finding method was proposed. Sliding cable element was used for simulation in order to reduce element bending moments，the general steps were given，and then a test was carried out to verify the proposed method. The conclusion was drawn from the internal force comparison that this method can effectively reduce element bending moments and the result is ideal. This method also shows such advantages as easy operation，no iteration or programming and very short consuming time. By optimizing the result with form-finding，this method can further reduce unit bending moments. By analyzing the effect of classification joint position changes on the result of form-finding and summarizing the rule，this method has the significance in engineering applications and provides some references for the analysis and design of tree structures.

tree structure；form-finding analysis；sliding cable element

TU318

A

0493-2137(2015)04-0362-11

10.11784/tdxbz201309030

2013-09-09；

2013-11-22.

天津市科委基金资助项目(11ZCZDSF04800)．

张 倩（1985— ），女，博士研究生，popzhqly@163.com.

王小盾，maodun2004@126.com.