一种改进的自然梯度语音信号盲分离算法

岳建杰，赵旦峰，张成

1．哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001

2．哈尔滨工程大学自动化学院，黑龙江哈尔滨 150001

一种改进的自然梯度语音信号盲分离算法

岳建杰1，赵旦峰1，张成2

1．哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001

2．哈尔滨工程大学自动化学院，黑龙江哈尔滨 150001

自然梯度算法有较快的收敛速度、良好的分离性能，在盲信号分离中占有重要地位。基于自然梯度的盲源分离算法一般分为固定步长和变步长的自然梯度算法，固定步长的自然梯度算法存在分离速度与稳定性之间的矛盾，即步长越长时分离速度快，但是稳态误差又得不到保障；步长太小分离速度又达不到要求。为了改善分离速度与稳定性之间的矛盾，提出了一种变步长的方法来，并用其改进了固定步长的标准自然梯度算法，成功地用于混合语音信号的分离，该方法取得比标准自然梯度算法更好的分离效果，具有更快的收敛速度。

语音信号处理；自然梯度算法；收敛速度；盲信号分离

盲信号分离起源于鸡尾酒会问题［1］，在鸡尾酒会场景下，没有源信号的任何先验信息，只知道混合的观测信号，这就使得盲信号分离成为了解决无源信号问题的最好方法，因为这种估计源信号方法无需知道混合过程的参数等信息［2］。盲信号分离最基本的方法就是独立分量分析（independent compo-nent analysis，ICA）的方法，其中Fast ICA算法［3］、随机梯度算法［4］、自然梯度算法［5］、EASI算法［6］、迭代求逆等方法都是常用的算法，这些算法都是最小均方（leastmean square，LMS）型的算法。LMS算法有着固有的缺陷，就是稳态误差和步长成正相关性，收敛时间和步长成反相关性，这就使得这一类型的算法收敛速度和稳态误差特性不能同时得到满足［7］。为了改善这种状况，本文对前人自然梯度算法［8-11］进行深入研究，采用文献［12］中把固定步长改变成变步长的思想，不仅大大提高了自然梯度算法分离效率，而且大幅提升了分离的收敛速度。

1 盲信号分离问题

语音信号盲分离问题瞬时混合模型通常如图1所示。

图1 混合系统

s(t)＝[s1(t)，s2(t)，…，sm(t)]T是n个说话者声音信号组成的n维向量；x(t)＝[x1(t)，x2(t)，…，xm(t)]T是m个观测信号组成的m维向量，其元素是各个麦克风的输出；A是m×n维矩阵混合矩阵，其元素aij表示信号的混合情况，如果为语音信号，取决于第i个说话者和第j个麦克风之间的距离。即

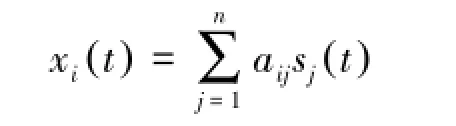
或者简记为

x(t)＝As(t)

盲信号分离问题的提法就是只根据观测信号数据x(t)求得分离矩阵W，W是A的逆矩阵，使得变换后的输出

y(t)＝Wx(t)

是源信号s(t)的一个估计或拷贝。

1．1 信号分离的前提假设

为了保证ICA模型是可解的，做出如下3个合理假设，第1个假设就是源信号s t()为平稳随机向量且各个源信号是统计上相互独立的；第2个假设就是源信号中最多只有一个高斯信号，因为多个高斯信号的混合还是高斯信号，信号不可能被分开；第3个假设就是为了简化估计，未知的混合矩阵是一个方阵且混合矩阵是行满秩的，即独立源信号的数目和观测信号的数目是相等的。如果当信源的数目少于观测信号的数目时，可以利用主原分析（princi-pal component analysis，PCA）的方法降低维数使混合矩阵为一个方阵。只有这3个假设同时有效时，源信号s(t)才能从混合信号x(t)中被估计出来。

图2 盲信号分离框图

此时盲信号分离的实际过程如图2所示。

y(t)＝Wx(t)＝WAs(t)＝Cs(t)

式中C＝WA。

需要指出的是，对瞬时混叠信号盲分离，在源信号可以精确恢复的情况下应有W＝A－1。然而由于源信号和混叠矩阵都未知，在以上假设条件约束下的一般分离方法，盲源分离存在2个不确定性，即恢复的信号的幅度不确定性和信源各分量次序的不确定性。在许多应用背景下，绝大多数信息包含在信号的波形而不是信号的幅度和次序中，所以在瞬时混叠情况下，盲信号分离的这2个不确定性是可以接受的。

1．2 信号的预处理

混合信号盲分离前，需要对信号进行预处理，可以大大减少计算和分离效率。最有用的预处理步骤就是对观测信号去均值和白化，一些特殊的问题，要用低通或高通滤波器去除噪声信号或扰动［13］。

1．2．1 信号的零均值处理

盲信号分离算法中，源信号的分量变换成零均值，可以大大减少计算量，并且对分离结果无影响。

假设x是一个非零均值的随机变量，其去均值过程可以用x0＝x－E(x)来表示，在真实的计算情况下，算术均值通常由数学期望来估计：

式中：xi(t)是观测信号x(t)＝［x1(t)，x2(t)，…，xn（t）］T的一个分量，其中i＝1，2，…，N，t＝1，2，…，N是随机变量x的N个采样点。

1．2．2 信号的白化

盲信号分离中，白化是一个通用的改善分离性能的信号预处理方法，因而白化是非常有必要的。

2 自然梯度算法

梯度算法有等变化性等优良的性能，应用场合广泛，但存在步长与稳态误差间的固有矛盾。

2．1 标准自然梯度算法

在盲信号分离或ICA问题中，输出y（k）相互独立性反应了分离的性能，通常情况下使用K-L散度作为独立性的度量。文中使用py（y，W）作为随机变量y＝Wx的概率密度函数并且创造一个概率密度函数q（y），在q（y）中的所有分量都是在统计意义上独立的，并将其作为一个参考。当且仅当py（y，W）和q（y）同分布时，K-L散度才会是零，也不会随着变量yi的非线性变换而变化。独立性的自然度量表示为

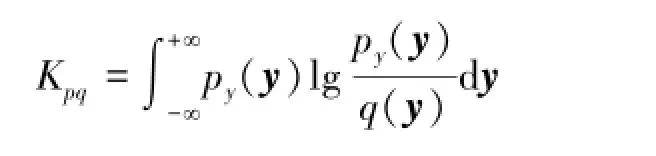
如果K-L散度由输出y的差分熵H(y)来表示

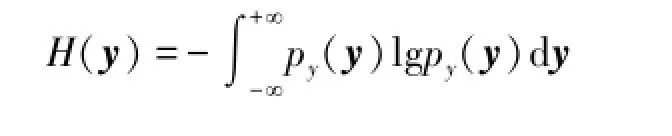
由文献［4］得到K-L散度的互信息和差分熵表示为

把式（1）、（2）代入式（3）得到

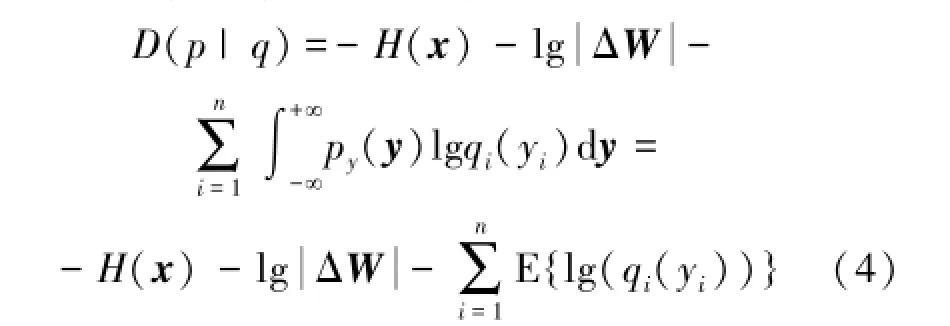
通过文献［13］中随机梯度在线学习算法，式（4）的广义梯度为

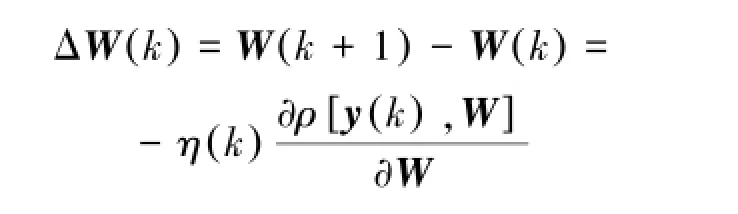
式中：η（k）是依赖于k的学习率，并且∂ρ／∂W是由元素∂ρ／∂wij组成的n×n的梯度矩阵。通过差分矩阵的操作，可以得到

式中f(y)＝[f1(y1)，f2(y2)，．．．，fn(yn)]T是一个列矢量，其第i个元素是

式中：(qiyi)是源信号{si}的概率密度函数的估计，梯度－∂ρ／∂W是欧几里得空间中目标函数最速下降方向。

文献［13］中提到，Amari等人把W引进了自然黎曼空间中并证明了参数W黎曼空间中最速下降的方向并不是标准的负梯度所指向的方向－∂ρ／∂W，而是

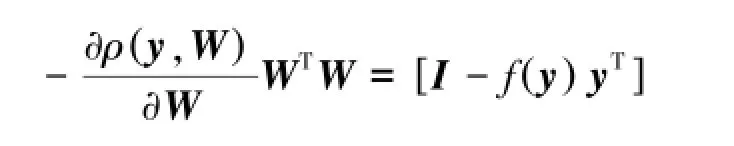
根据黎曼空间中参数的结构，这种自然梯度修改了标准梯度的搜索方向，但是并没有改变最小值点因而确保了参数估计的全局最优解。自然梯度有着等变化的性质，且不用求逆运算，不受混合矩阵变化的影响，并且没有像牛顿法在目标函数的均方估计，算法阻止了W(k)的畸变［14］，很适合目标函数非线性的模型。综上，推导可以得到自然梯度算法为

W(k＋1)＝W(k)＋η(k)[I－f(y)yT]W(k)文献［4］详细讲解了非线性函数f(y)的选择。

2．2 改进的自然梯度算

标准自然梯度算法有着很好的收敛与分离性能，但是其码间干扰收敛速度很慢，为了加速码间干扰的收敛速度，参考文献［12］将传统算法中分离矩阵的Frobenius范数变化情况强加于梯度学习算法，将使算法在学习过程中保持相对稳定，采用该思想方法有η（k）迭代调节过程如下：

取

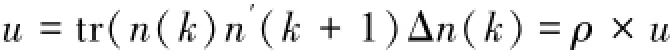
式中tr是求矩阵的迹，此时有

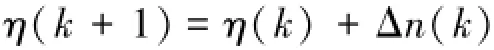
所以改进后的自然梯度算法表现形式仍然为

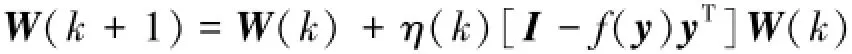
综上所述，改进的自然梯度算法的步骤如下：

1）对观测信号去均值、白化，选取非线性函数f(y)＝tan y；

2）初始化系统参数，选取迭代最大步数为l＝100步，ρ＝0．001，η（1）＝0．05，那么，

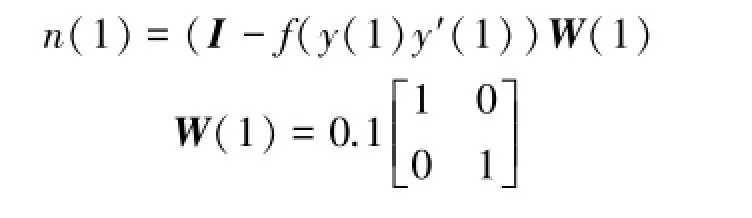
3）分别计算如下各式：

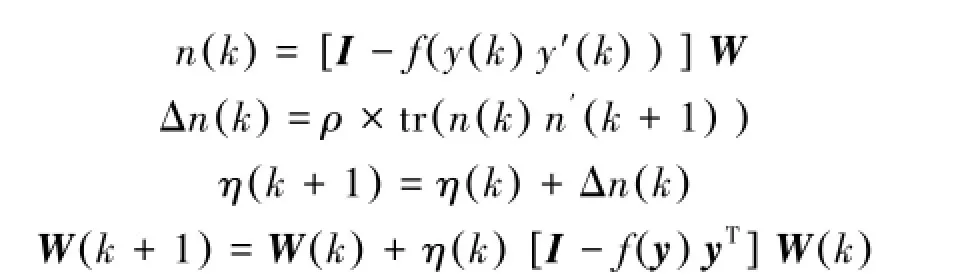
如果1＜lp≤100，则反复执行，直到l＝100执行完。

3 仿真实验及实验结果分析

选用2路纯净的语音信号进行算法的验证性分离试验，验证算法的有效性：其中s1内容是：“这就是去洛克菲勒中心的地铁吗？是”；s2内容是：“I’m interesting about education！”。使用MATLAB软件仿真，得到源信号s1和s2的波形图如图3所示。

图3 源语音信号

随机产生一个混合矩阵A，取3位有效数字得到

源信号s1和s2在混合矩阵A作用下混合得到混合观测信号，其中x1(t)和x2(t)的波形如图4。

图4 混合语音信号

对观测信号x(t)去均值，白化预处理后，用标准自然梯度算法和改进的自然梯度算法采取相同的参数和迭代步数，迭代计算出的分离矩阵分别为W1和W2，其值分别为

在MATLAB软件仿真环境下，仿真分离出的波形如图5、6所示。

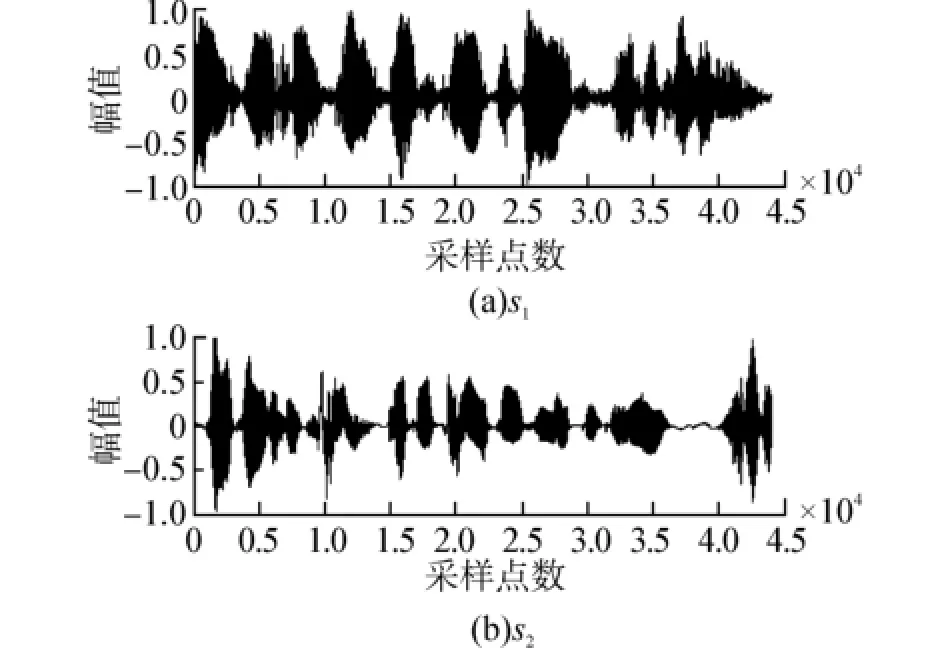
图5 标准自然梯度算法分离的信号

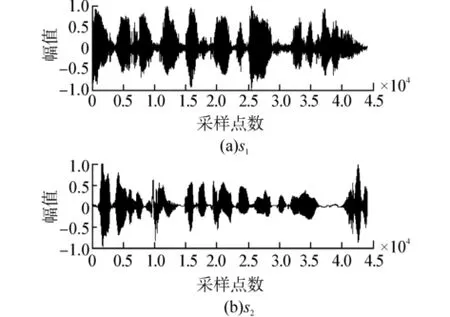
图6 改进自然梯度算法分离的信号

2种分离方法分离出的波形和原始语音信号的波形相比较，直观上分离结果波形相似度很高，由于自然梯度算法存在2种不确定性，所以需要引进分离性能评价指标。语音信号分离性能评价指标一般使用性能测度码间干扰（inter symbol interference，ISI）［13］作为分离性能的评价标准。码间干扰定义为

式中C＝WA，cij，cik分别表示矩阵C的i行j列和i行k列的元素。当信号得以精确分离时，指标I（C）应该为零，实际上一般为较小的值。文中2种分离方法同取ρ＝0．001，码间干扰曲线如图7所示。

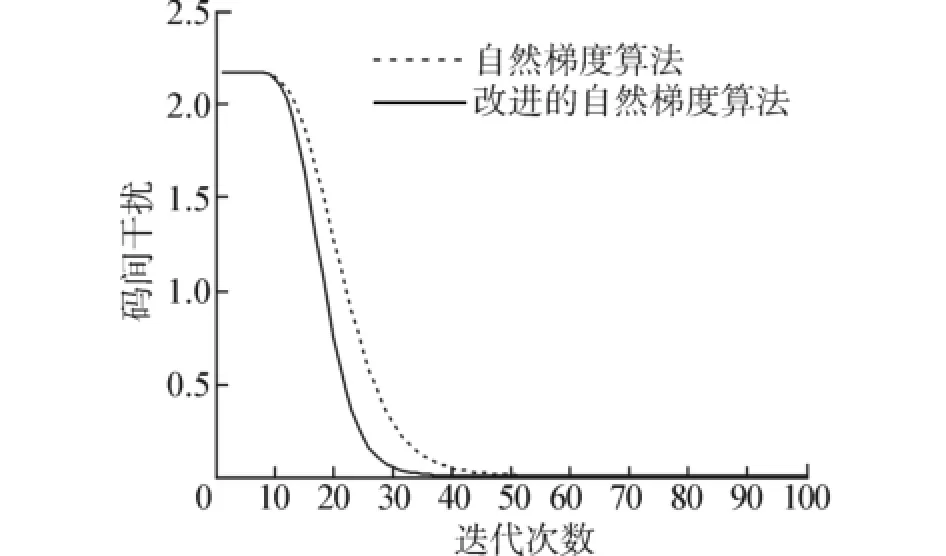
图7 2种自然头分离算法的码间干扰

从图7中看到这2种算法在分离的初始阶段码间干扰都很大，随着分离程度的加深，码间干扰很快的降低，最后稳定在一个很小的值，说明这2种分离算法都能将混合信号得到精确的分离。从图7中可以看出第10步迭代后码间干扰迅速下降，标准自然体算法码间干扰曲线迭代次数到了45步才稳定到一个很小的值；改进后的自然梯度法码间干扰曲线迭代到了35步就稳定到了一个很小的值。说明改进后的自然梯度算法收敛速度比原始的收敛速度有所提高。

选取不同的ρ得到码间干扰曲线如图8所示。

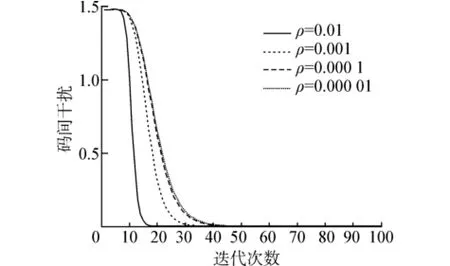
图8 不同ρ下的码间干扰误差

图8中所示，在改进的自然梯度算法中使用不同的ρ有着不同收敛速度。ρ＝0．0001和ρ＝0．00001这2条曲线几乎重合在一起，所以可以推得，当ρ小到一定程度时，码间干扰曲线几乎没有变化。由图8知，当ρ＝0．01时，在迭代次数20步的时候码间干扰都很小了，其他小于0．01的ρ的码间干扰迭代了30步以后才收敛到一个很小的数，所以ρ越小码间干扰收敛的速度越慢，从图中看出ρ＝0．01时收敛的速度几乎是直线下降，所以在算法中取ρ相对大一些更符合实际要求。

4 结束语

运用标准自然梯度和改进的自然梯度算法都能将混合的语音信号分离开来，通过对比标准自然梯度算法和改进的自然梯度算法分离结果的串音误差曲线，二者都具备很好的分离性能，改进后的自然梯度算法具有更快的分离速度，这种更快的分离性能用在实时性要求更高的环境中就能获得更好的分离效果。在此考虑的都是纯净的语音信号，而在真实的环境中不可避免受到噪声信号的干扰，今后研究噪声污染的信号的分离更具有实际的意义。

［1］HAYKINS，CHENZ．The cocktail party problem［J］．Neu-ral Computation，2011，17（9）：1875-1902．

［2］CHOIS，CICHOCKIA，PARK H M，et al．Blind source separation and independent component analysis：a review［J］．Neural Information Processing-Letters and Reviews，2005，6（1）：1-57．

［3］PRASAD R PR．Fixed-point ICA based speech signal sepa-ration and enhancement with generalized Gaussian model［D］．Ikoma：Nara Institute of Science and Technology，2010：89-96．

［4］杨福生，洪波．独立分量分析的原理与应用［M］．北京：清华大学出版社，2006：15-50．

［5］SANDIKO C M，MAGSINO E R．A blind source separation of instantaneous acoustic mixtures using natural gradient method［C］／／2012 IEEE International Conference on Con-trol System，Computing and Engineering（ICCSCE）．Mel-bourne，Australia，2012：124-129．

［6］CARDOSO JF，LAHELD BH．Equivariant adaptive source separation［J］．IEEE Transactions on Signal Processing，2009，44（12）：3017-3030．

［7］裴学广．基于变步长自然梯度算法的盲源分离［J］．舰船电子对抗，2007，30（4）：65-68．

［8］马建仓，冯冰，程存虎，等．自然梯度盲分离算法在振动信号处理中的应用［J］．火力与指挥控制，2011，36（4）：154-157．

［9］付卫红，杨小牛．改进的基于步长自适应的自然梯度盲源分离算法［J］．华中科技大学学报：自然科学版，2007，35（10）：18-20．

［10］李广彪，张剑云．基于分离度的步长自适应自然梯度算法［J］．信号处理，2009，23（3）：429-432．

［11］刘颖超，张纪元．梯度下降法［J］．南京理工大学学报：自然科学版，1993（2）：2-5．

［12］张天骐，李雪松，夏淑芳，等．梯度自适应在线ICA的改进［J］．北京邮电大学学报，2010，33（5）：108-111．

［13］史习智．盲信号处理——理论与实践［M］．上海：上海交通大学出版社，2011：61-85．

［14］BENESTY J．An introduction to blind source separation of speech signals［M］．New York：Springer，2000：321-329．

Speech signal blind source separation based on an im proved natural gradient algorithm

YUE Jianjie1，ZHAO Danfeng1，ZHANG Cheng2
1．College of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China
2．College of Automation，Harbin Engineering University，Harbin 150001，China

A natural gradient algorithm has a fast convergence rate and excellent separation property，and thus plays an important role in blind signal separation．The blind source separation algorithms based on natural gradient are commonly classified into fix-step-size and variable step-size algorithms．The fix-step-size natural gradient algorithm has the inherent contradiction between the speed of separation and the error in steady state．Namely the bigger the step size is，the faster the separation speed is，but the error in steady state cannotmeasure up．Then a small step size would lead to slow separation speed．In order to improve the contradiction，this paper proposes a new method based on variable step-size natural gradient，which is used to improve the fixed-step-size standard natural gradient algorithm and it has been successfully applied to separatemixed speech signals．The new algorithm has gained bet-ter separation performance and faster convergence speed in inter symbol interference than the standard one．

speech signal processing；natural gradient algorithm；convergence rate；bind signal separation

TN971．1

A

1009-671X（2015）03-030-05

10．3969／j．issn．1009-671X．201409015

2014-09-25．

日期：2015-04-20．作者简介：岳建杰（1986-），男，硕士研究生；赵旦峰（1961-），男，教授，博士生导师．

岳建杰，E-mail：348274742＠qq．com．

http：／／www．cnki．net／kcms／detail／23．1191．U．20150420．1055．011．html