基于能量平衡的无线传感器网络分布式成簇机制

冯冬青,邢凯丽

(郑州大学电气工程学院,河南郑州450001)

基于能量平衡的无线传感器网络分布式成簇机制

冯冬青,邢凯丽

(郑州大学电气工程学院,河南郑州450001)

针对资源有限的无线传感器网络目标跟踪问题，采用一种基于能量平衡的最优分布式成簇机制，为此引入了基于节氛剩余能量标准差的能量平衡指标，将其转化为多目标约束优化问题，并采用二进制粒子群优化算法求取最优解.Matlab仿真结果表明，与基于能耗和扩展卡尔曼滤波的成簇机制相比，采用基于能量平衡的最优成簇机制能在保证跟踪精度和能量平衡的前提下，提高网络寿命近2倍，从而有效地延长了网络寿命.

无线传感器网络;目标跟踪;能量平衡;成簇;网络寿命

0 引言

无线传感器网络(Wireless Sensor Networks, WSNs)是一种新兴的自组织网络,它在目标跟踪领域有着良好的应用前景.实际应用中,因传感器节点的感知半径、存储、通信、数据处理能力、网络带宽及节点能量都十分有限,所以必须动态地管理调度网络资源来进行协同信号与信息处理［1］.

WSNs应用于目标跟踪时,通过分簇机制来优化网络拓扑结构,从而达到均衡网络能耗、延长网络寿命的目的.文献［2-4］中分簇机制仅仅考虑了网络总能耗而忽略了能量平衡,从而容易导致网络出现断连、信息丢失等现象.目前,有些文献提出了基于能量平衡的分簇机制,如文献［5］基于簇头间能量平衡来延长网络覆盖时间;文献［6］建立了一种能量平衡模型,并考虑了网络总能耗和簇头与簇盟员节点剩余能量差;文献［7］通过最小化最大的任务节点间剩余能量的能耗差来平衡监测区域内局部能量.但是,文献［5-7］只考虑了部分任务节点的能量平衡,未考虑到网络寿命与每个节点的剩余能量有关,因此,这些分簇机制仍可能会导致整个网络能量分布不平衡,缩短网络寿命.鉴于此,笔者采用工作区域内节点剩余能量的标准差来衡量网络能量平衡程度,进而引人了一种新的能量平衡指标,不仅节省总能耗,而且兼顾考虑了网络中节点剩余能量的分布程度.

另一方面,当前用于解决非线性条件下目标跟踪问题的滤波方法中,无迹卡尔曼滤波(UKF)的应用较为广泛.为了提高UKF的跟踪精度,需要调度多个任务传感器节点去感知目标,这样会增加网络消耗,缩短网络寿命.

综上所述,为了寻找一种最优成簇机制,需综合考虑影响网络寿命的能量平衡和跟踪精度这两个因素.笔者将其转化为多目标约束优化问题,并采用了二进制粒子群优化算法寻求最优解.

1 UKF算法

笔者采用式(1)目标状态模型:

式中:X(k)为k时刻系统的状态向量;W(k)是均值为零、协方差矩阵为Qk的状态高斯白噪声.

假设WSNs是由一组同构传感器节点随机分布组成的,各个节点的坐标位置是已知的,而且其探测半径r相同.在第k时间步有Nk个节点被唤醒探测目标,其中调度Lk个节点,形成任务簇,其测量模型如下:

式中:Z(k)为测量向量;V(k)是均值为零、协方差矩阵为Rk的测量高斯白噪声.

针对目标状态模型(1)和测量模型(2),笔者采用UKF实现对目标状态的预测估计,具体公式见文献［8］.系统在获取k+1时刻的测量值后,通过UKF得到了k+1时刻的状态的估计值和协方差从而目标状态估计的均方误差可表示为

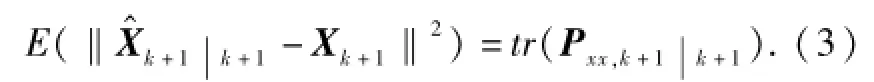
2 能量平衡的最优成簇机制

目标进人监测区域后,首先被传感器节点内置的被动红外传感器探测到,其唤醒所属的传感器节点,被唤醒的Nk+1个节点构成候选簇员集合Γ=之后,唤醒节点根据自身位置k+1和能量给出回复信息,上一簇头CHk根据回复信息按照某种成簇机制调度部分唤醒节点形成下一簇C,包括簇头CH和簇盟员的k+1k+1选择;最后CHk将目标状态和方差发送给CHk+1.簇Ck+1形成后,各簇员节点执行目标感知任务,簇盟员节点发送测量值到CHk+1,CHk+1根据UKF算法估计目标位置.在目标的移动过程中,将动态地生成新的簇来实时跟踪.

2.1 采用改进的BPSO进行跟踪传感器的选择

PSO算法中第i个粒子在第t代的状态表示为

式中:D为待求解问题维数;Xi(t)和Vi(t)为粒子群中第i个粒子在第t代的位置和速度.

第i粒子在D维搜索空间中飞行状态的速度和位置更新为:

BPSO算法［9］将粒子的位置定义为一个二进制的1/0串,来表示候选传感器被选择与未被选择的信息.不同于式(6),由于BPSO中处理的是离散变量,所以不能通过算术的方式对位置和速度进行相加,需要适当地修改.

2.2 适应度函数的构造

在目标跟踪成簇过程中,能量消耗集中在上一时刻簇头和目标探测范围内的节点上(即工作区域).因此,笔者在衡量网络能量平衡程度时,采用了工作区域内节点剩余能量的标准差,并通过确保网络能量平衡性来延长网络寿命.

首先选择离目标最近的节点作为初始簇头CH0.从Γk+1中调度部分节点形成一个候选簇=={,∈Γ,CH"为C′的簇头,为k+1k+1k+1中簇成员节点集合.工作区域内节点的能量消耗源于簇头CHk发送目标状态估计值和方差到下一时刻簇头CHk+1,簇成员节点感知目标并发送测量值到簇头,簇头感知目标并接收CHk发送的目标状态估计值和方差,同时接收发送的测量值.根据传感器能耗模型［10］,CHk、、CH"k+1的能耗分别为

式中:ut、ud及ur均为常数,其中ut和ud由发送端配置［10］,ur由接收端配置［10］;us为传感器感知单位数据消耗的能量;b1为CHk发送数据位数, b2i、b2分别为、CH"k+1所获测量值位数; d(·)为两点间距离函数.则簇C′k+1内总能耗为

下面通过内搜索方法,确定该候选簇C′k+1中最优的簇头CH′k+1和盟员节点CM′k+1,

从而,第k+1时间步工作区域节点的剩余能量的标准差为

其中,std(·)是标准差函数.引人一个新的能量平衡指标

其中,ε1∈［0,1］为权重参数,用来折中总能耗与能量平衡.此外根据式(3),候选簇C′k+1对应的跟踪精度为f′k+1,2=tr(.

在WSNs目标跟踪过程中,由于成簇的基本准则是保证良好的能量平衡和较高的跟踪精度,因此,基于BPSO算法的最优成簇机制的适应度函数是对f′k+1,1和f′k+1,2的加权和,如式(20)所示:转(4).

式中:ε2∈［0,1］,为权重参数;γ是能量匹配因子,使能量平衡指标与跟踪精度有相同的数量级.

2.3 算法步骤

通过前面的分析,能量平衡的最优成簇问题最终转化成从唤醒节点中寻求一个满足min的候选簇.基于BPSO算法的最优成簇机制具体实现如下.

(1)当Γk+1=φ时,Ck+1=CHk,否则执行步骤(2).

(2)初始化.对种群的M个粒子进行随机初始化.第i个粒子的位置Xi(t)随机初始化为二进制1,0串;速度Vi(t)初始化为［-Vmax,Vmax］之间的随机向量.设置参数c1=c2=2.0,当前代数t=0.

(4)对第i个粒子,进行如下操作:ⓐ使用公式(5)对其速度进行更新;如果速度Vi越过边界［-Vmax,Vmax］,则将Vi设为边界;ⓑ使用公式(7)对粒子位置进行更新;ⓒ对第i个粒子的新位置进行评估.如果(Xi(t+1))＜(Pi),则Pi=Xi(t+1);那么(Pi)＜(Pg),则Pg=Pi.

(5)t=t+1.如果t＞Max Gen,则转(6),否则

(6)输出Pg.最后寻出第k+1时间步的最优簇Ck+1.如果Ck+1=φ,则执行(1).

3 实验及分析

在Matlab环境下,笔者对以下3种成簇机制进行了对比实验:①基于能量平衡的最优成簇机制(CSEB),即笔者所提出的成簇机制;②基于能耗的成簇机制(CSBQN),此机制仅考虑了能耗,式(19)中ε1=1;③基于扩展卡尔曼滤波(EKF)的成簇机制(CSEKF),与CSEB相比,采用了EKF滤波算法.

3.1 仿真参数设置

在100 m×100 m的矩形监测区域内,随机散布50个传感器节点,每个节点的探测半径r= 20 m,除了节点6#、11#、12#和29#的初始能量设为0.2 J外,其余节点的均设为0.5 J,以构成一个能量不平衡的网络,终止代数为20,其他参数设置见表1.其中ε1选取为0.5,在式(19)中,总能耗与能量平衡对f′k+1,1的影响均衡.若ε1选取得过大,会导致簇内某节点能耗过多使得网络出现断连、能量空洞、信息丢失;ε1选取得过小,忽略成簇机制总能耗,则会造成能源浪费.

整个实验仿真时间是50个时间步,目标在0～10,24～27,40～50时间步内做线性运动,其他时间步内做圆弧运动.

表1 仿真参数设置Tab.1 Setting of simulation parameters

3.2 仿真结果分析

图1表示CSEB下的目标跟踪,与实际目标之间用虚线相连的小三角表示该传感器节点被选为了簇头.图2给出了3种机制下相应的跟踪误差.在线性运动阶段,3种机制都能较好地跟踪目标;在圆弧阶段,CSEB、CSBQN仍能较好地跟踪目标,然而CSEKF已不能较好地跟踪目标,跟踪轨迹偏离了实际轨迹.因此,UKF相比EKF来说,在复杂的非线性运动中有更好的跟踪精度.

图1 CSEB机制下的跟踪效果Fig.1 Tracking trajectory under CSEB

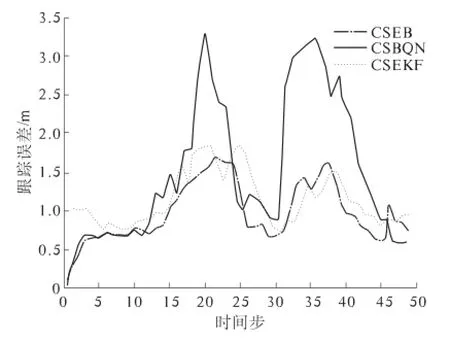
图2 不同成簇机制下的跟踪误差比较Fig.2 Tracking errors comparison under different clustering mechanisms

图3给出了不同成簇机制下各时间步在工作区域内节点的剩余能量标准差.CSEB和CSEKF为了保证能量平衡,在调度节点时可能会选择距离目标较远的节点,而未选择距离目标较近但剩余能量较少或是调度次数较多的节点;CSBQN为了减少能耗会调度较少且距离目标较近的节点,一些节点如6#、12#、29#会被多次调度,所以CSBQN的标准差比CSEB和CSEKF都大.上述结果表明,与CSEKF和CSBQN相比,CSEB能较好地完成非线性运动目标跟踪,同时还保证了网络能量的平衡性.

图4给出了完成目标跟踪后3种机制下的节点剩余能量.表2给出了不同机制下整个网络的总能耗、总剩余能量和网络寿命.在CSBQN中,节点6#在完成跟踪任务之前其剩余能量已经不足以去实现跟踪,它的网络寿命只有17时间步(见表2);然而,CSEB和CSEKF均考虑了能量平衡,很少调度节点6#和12#来避免节点死亡,其网络寿命大于50时间步.此结果表明,CSEB能够在保证能量平衡的前提下延长网络寿命.

图3 不同成簇机制下工作区域内节点的剩余能量标准差Fig.3 Standard deviations of the residual energy in the working area at each time step under different clustering mechanisms

图4 不同机制下节点剩余能量的比较图Fig.4 Node residual energy comparison under different clustering mechanism s

表2 不同机制下整个网络的总能耗、总剩余能量和网络寿命Tab.2 Total energy consumptions，total residual energy and network lifetime of the network under different mechanisms

4 结论

在无线传感器网络资源有限的前提下实现对目标的实时跟踪是一项极具挑战性的任务.笔者采用了一种能量平衡的最优分布式成簇机制,与基于能耗和扩展卡尔曼滤波的成簇机制相比,此机制能在保证跟踪精度和能量平衡的前提下,提高网络寿命近2倍,从而有效地延长了网络寿命.该机制容忍了能量不平衡网络,并通过确保网络能量平衡性来有效地延长网络寿命,同时又保证了跟踪精度,有效地避免了网络能量不平衡.

［1］ THARMARASA R,KIRUBARAJAN T,SINHA A,et al.Decentralized sensor selection for large-scalemu ltisensor-multitarget tracking［J］.IEEE Transactions on Aerospace and Electronic Systems,2011,47(2): 1307-1324.

［2］ LIU Xue-feng,CAO Jian-nong,LAIS,et al.Energy efficient clustering for WSN based structural health monitoring［C］//Proceedings of IEEE Con ference on Computer Communication.Shanghai:IEEE Press, 2011:2768-2776.

［3］ MAHMUD S,WU Hui,XUE Jing-ling.Efficient energy balancing aware multiple base station deployment forWSNs［C］//Proceedings of 8th European Conference on W ireless Sensor Networks.Berlin:Springer, 2011:179-194.

［4］ AMINI N,VAHDATPOUR A,XU Wen-yao,et al. Cluster size optimization in sensor networks with decentralized cluster based protoco-ls［J］.Computer Communications,2012,35(2):207-220.

［5］ SHU T,KRUNZ M.Coverage-time optimization for clustered wireless sensor networks:a power-balancing approach［J］.IEEE/ACM Transactions on Networking,2010,18(1):202-215.

［6］ LIU Yong-gui,XU Bu-gong,FENG Lin-fang.Energybalanced multiple sensor collaborative scheduling for maneuvering target tracking in wireless sensor networks［J］.Journal Control Theory Application,2011,9 (1):58-65.

［7］ ZHANG Jian,WU Cheng-dong,ZHANG Yun-zhou, et al.Energy-efficient adaptive dynamic sensor scheduling for targetmonitoring in wireless sensor networks［J］.ETRI Journal,2011,33(6):857-863.

［8］ JULIER S J,UHLMAN J K.Unscented filtering and nonlinear estimation［J］.IEEE Trans Automat Contr, 2004,92(3):401-422.

［9］ SHIRIN K,KARIM F,AMJAD O.Modified discrete binary PSO based approach to sensor placement in WSN networks［C］//Proc of the International Conference on Computational Intelligence and Communication Systems.Bhopal:IEEE Press,2010:200-204.

［10］LIN Jian-yong,XIAO Wen-dong,LEW IS F L,et al. Energy efficient distributed adaptive multi-sensor scheduling for target tracking in wireless sensor networks［J］.IEEE Transactions on Instrumentation and Measurement,2009,58(6):1886-1896.

A Distributed Clustering Mechanism Based on Energy Balance in Wireless Sensor Networks

FENG Dong-qing,XING Kai-li
(School of Electrical Engineering,Zhengzhou University,Zhengzhou 450001,China)

Focusing on the target tracking problem in resource-constrained wireless sensor networks,a novel energy-balanced optimal distributed clustering mechanism is adopted by introducing an energy-balanced index based on the standard deviation of residual energy of nodes.Then,it is transformed into a multi-objective constrained optimization problem,and a binary particle swarm optimization algorithm is employed to solve this problem.Simulation results in Matlab environment show that the energy-balanced optimal distributed clustering mechanism guarantees energy balance and tracking accuracy comparing with the clustering mechanisms respectively based on the energy consumption and the extended Kalman filter,and that it improves the network lifetime of nearly 2-fold,effectively prolonging the network lifetime.

wireless sensor network;target tracking;energy balance;clustering;network lifetime

TP393

A

10.3969/j.issn.1671-6833.2015.03.002

1671-6833(2015)03-0006-05

2015-01-20;

2015-02-04

国家自然科学基金资助项目(60973094)

冯冬青(1958-),男,广东佛山人,郑州大学教授,博士,主要研究领域为智能控制理论与应用,E-mail: dqfeng@zzu.edu.cn.