新型实用合环潮流算法在配电网中的应用
戴 晖, 孙 波
(淮安供电公司,江苏淮安211700)
目前国内10 kV和20 kV配电网系统多采用闭环设计、开环运行的供电方式[1]。在倒负荷和检修时,通过合、解环操作可以减少停电时间,提高供电可靠性。但由此引起的合环电流可能使馈线开关保护误动,造成停电。因此合环潮流计算需要很高的准确性,以达到提高供电可靠性和配网安全运行的目的。传统的配电网潮流算法主要为:回路阻抗法[2]、前推回代法[3]和改进牛顿法[4]。对于配电网环网的潮流计算,文献[5]提出分布系数法的潮流计算方法,该方法由于是手工计算,只适合简单网络的合环潮流;文献[6]提出了计算环状配电网的三相潮流“两阶段”法。该方法以支路电流为变量,计算存在一定的误差。文中提出了以支路功率为变量的基于叠加原理和前推回代法的两阶段算法计算配电网合环潮流。
1 基于支路功率为变量的前推回代法
文献[7]对如图1所示的辐射状配电系统,配电潮流前推回代算法的第m步迭代过程如下。
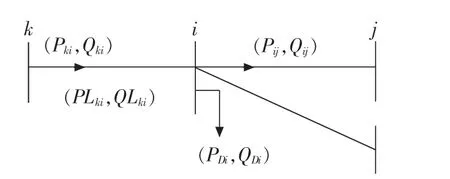
图1 辐射状配电系统
节点i的前推计算公式为:
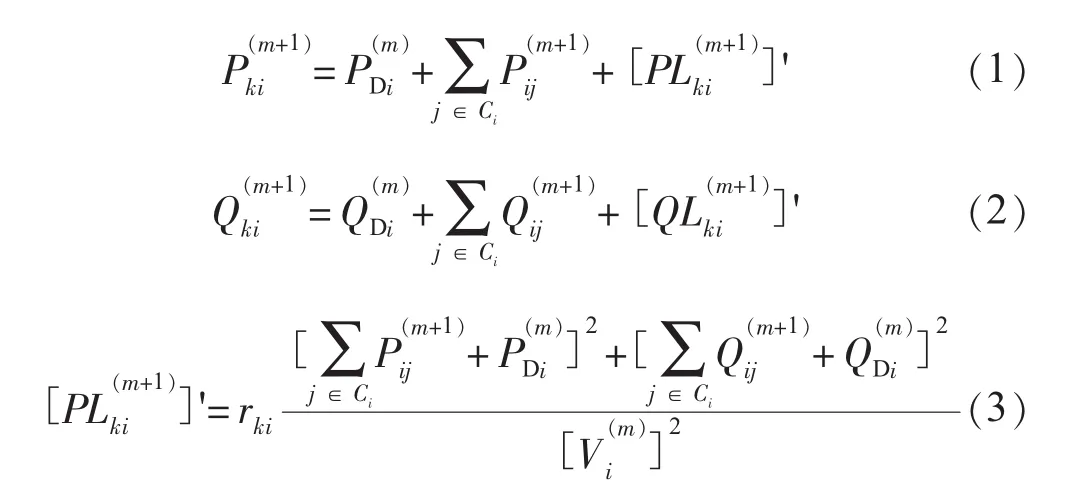

回代节点i电压时,节点k作为节点i的父节点,其电压已经在本次迭代中算出,节点i的回代公式为:


2 新型合环潮流计算
2.1 利用叠加原理分解合环配电网络
由于前推回代法只适用于辐射型网络,因此对于合环后的环网,利用叠加原理对前推回代法进行改进,在合环点处将环网打开,对合环开关两侧负荷功率进行修正,如图2所示。
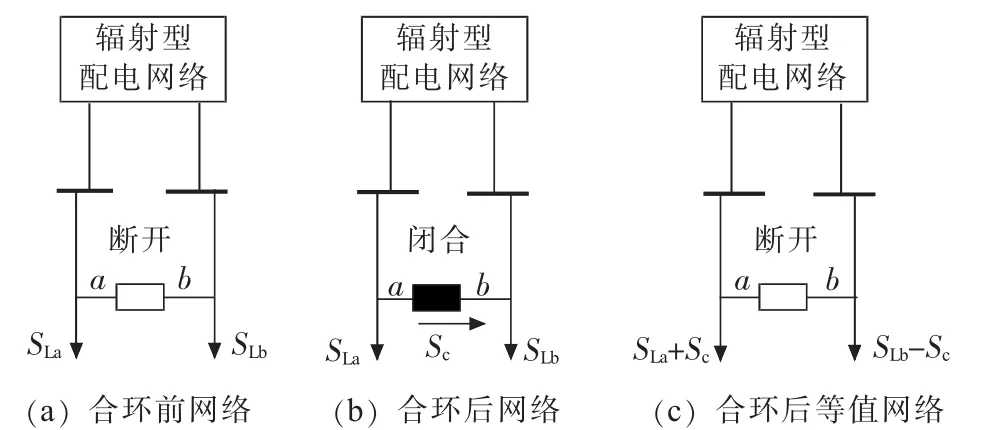
图2 配电网络合环模型
图2(a)中a、b为待闭合合环开关的两侧节点,合环前所带负荷分别为图2(b)为合环后示意图,合环开关闭合后由a、b两侧节点电压差所产生的环网功率Sc,相应的电流为Ic。若合环前为模拟合环时的状态在节点a添加一个电流源,方向为流出,在节点b添加一电流源,方向为流入,大小均为Ic。图2(c)为合环后等值网络,将环网功率Sc分别转移到负荷点a、b上,即a节点负荷为节点负荷为若合环前则电流源的符号相反。
应用戴维南定律将图2(b)中原辐射型网络等效为一个理想电压源和一个串联内阻如图3所示。其中电压源的值为合环前a和b节点的电压差可在合环前通过前推回代法进行潮流计算得到为戴维南等效阻抗。当网络中所有电源电势都为零时,所加的单位电流只流经环路上支路。所以即为从母线Ⅰ到母线Ⅱ合环线路中所有支路阻抗和。合环后稳态环流Ic为:
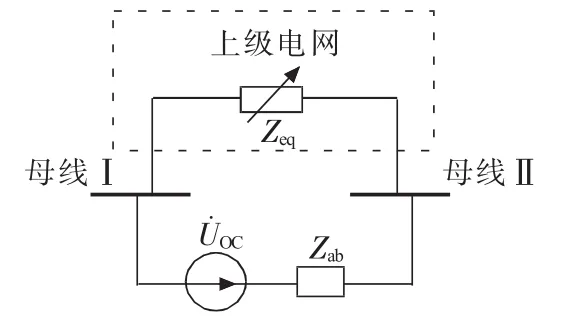
图3 合环稳态环流计算等值电路
配电网合环涉及上级电网,所以需对上级电网进行等值,Zeq为上级电网等值阻抗,这样可以求得环网功率Sc,难点是Zab的求取。
2.2 迭代法求上级电网等值阻抗
针对从不同变电所引出2条出线的环网,配电网合环网络与上级电网之间存在边界节点的特点,文中利用迭代法求取上级电网等值阻抗Zeq。根据母线Ⅰ、Ⅱ参数,选取电压值高的一侧为平衡母线,可计算出母线Ⅱ处的电压幅值为:
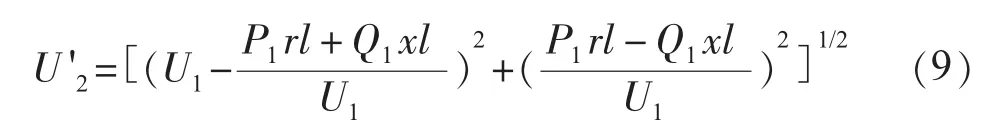
式中:P1为流过母线Ⅰ的有功功率;Q1为无功功率。z=r+j x为根据实际上级电网的特点,设定的虚拟线路单位长度的阻抗;l为虚拟线路长度。设计误差函数则为:

2.3 配电网合环潮流计算步骤
配电网合环潮流计算分两阶段迭代,第一阶段迭代按式(1—7)计算纯辐射型网络潮流和值,第二阶段迭代以环路功率为变量叠加修正,按式(11—14)修正合环开关两侧节点负荷功率,第m+1次迭代过程如下:
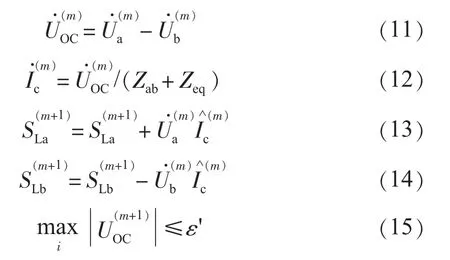
阶段一:
(1)读入网络参数,建立节点链接表。
(2) 按式(9)、(10)通过迭代法求得上级电网的等值阻抗Zeq。通过拓扑分析从合环点向上搜索,将合环支路的阻抗与上级电网的等值阻抗Zeq相加而得合环环路的总阻抗。
(3)按式(1—7)通过前推回代计算纯辐射网络潮流。按式(11)计算断开合环点处开口电压。
(4)按式(12)求得合环稳态环流。
阶段二:
(1) 按式(13)、(14)修正合环开关两侧节点负荷功率。
(2)检查迭代终止判据式(15),若不满足则转到阶段一中(3)、(4)。
3 算例分析
选取淮安盱眙10 kV配网系统的3个典型的馈线联络开关合环算例进行了计算。在PC机上用VB6.0进行了该算法的程序编制。算例中两阶段的收敛判据ε、 ε'都为 10-5。 算例结果(见表 1和表 2)表明,准确率较高,满足工程要求。
从表1可以,看出文中算法计算出的合环馈线电流值与测量值比较接近,但是仍然存在一定的误差,主要有以下几个方面:
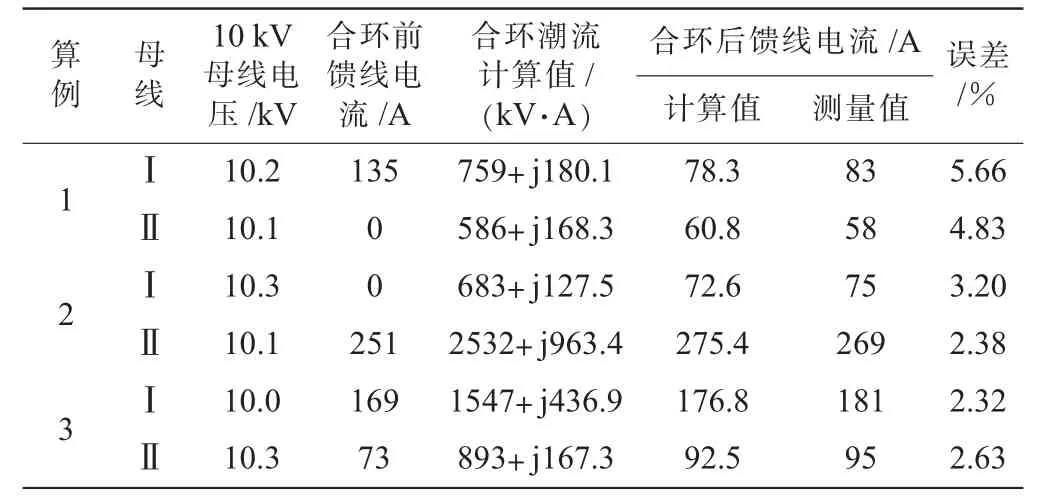
表1 计算结果
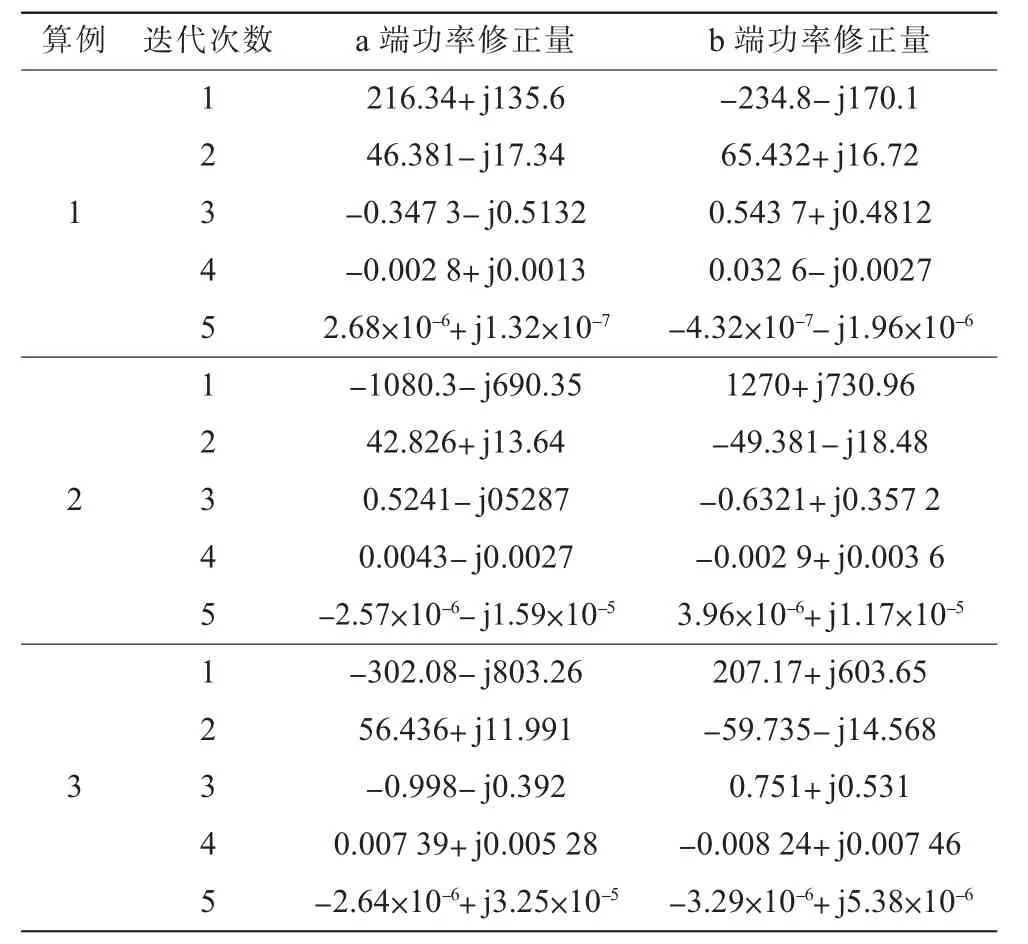
表2 迭代过程中的功率修正量 kV·A
(1)由于无法获取上级电网模型,因此无法准确获得上级电网的阻抗,采用迭代法虽简化了上级电网,但求得的等值阻抗对合环潮流计算存在一定的误差。
(2)数据采集与监视控制系统遥测量、遥信量的准确程度影响计算精度。
(3)功率因数无法获得。由于实际运行时,网测的数据有些是电流值,不是P、Q值,需要用电流值和功率因数推倒出P、Q值,而功率因数也非实测值,所以功率因数的准确与否对合环计算的误差有一定影响。该方法取功率因数为0.9。
从表2中可以看出,随着迭代次数的增加,合环开关两侧功率修正量的值逐渐减小。在第二阶段迭代到5次左右功率修正量的值几乎接近零。可见文中提出的算法具有很好的收敛性,从而提高了计算速度。
4 结束语
根据实际配网中的特性,提出的以支路功率为变量的基于叠加原理和前推回代法的两阶段算法,较好解决了配电网合环潮流计算难度大、误差大的难题,提高了合环潮流计算的准确性,在实际合环操作中,对调度员能否合环操作起到了指导作用,提高了合环操作的可靠性、安全性,具有一定的理论和工程实用价值。
[1]强兴华.地区电网合环操作的潮流近似计算[J].江苏电机工程,2002,21(5):34-35.
[2]车仁飞,李仁俊.一种少环配电网三相潮流计算新方法[J].中国电机工程学报,2003,23(1):74-79.
[3]陈根军,王 磊,唐国庆.一种求解环状配电网潮流的有效算法—两阶段法[J].电力系统及其自动化学报,2001,13(5):5-9.
[4]李家睿.复杂配电网网络等效及合解环潮流计算研究[D].上海:上海交通大学硕士论文集,2012.
[5]W ILLISH L.配电系统规划参考手册[M].范明天,等译.北京:中国电力出版社,2013:122-126.
[6]季晓明,成乐详.基于突变理论的配电网规划方案综合评估[J]. 江苏电机工程,2014,33(5):51-54.
[7]夏 翔,熊 军,胡列翔.地区电网的合环潮流分析与控制[J].电网技术,2004(22):77-80.

